大气消光系数垂直分布模型及其适用性研究
2018-07-26邓佩云倪长健朱育雷成都信息工程大学大气科学学院四川成都60225高原大气与环境四川省重点实验室四川成都60225
邓佩云,倪长健,2*,朱育雷 (.成都信息工程大学大气科学学院,四川 成都 60225;2.高原大气与环境四川省重点实验室,四川 成都 60225)
随着我国社会经济的迅猛发展,以颗粒物尤其是细颗粒物为代表的大气污染问题日益突出,并呈现出区域化和复合型的特征[1-3].颗粒物垂直分布是大气环境研究的重要内容,在灰霾持续恶化的背景下,其重要性愈加受到学界的关注[4].Wu等[5]通过对澳门城市道路旁2~79m范围内细颗粒物11h的监测结果表明,细颗粒物质量浓度随高度增加呈递减趋势;杨龙等[6]利用中国科学院大气物理研究所内325m铁塔资料,发现北京秋冬季近地层 PM2.5质量浓度随高度的增加以对数规律递减;孙玫玲等[7]基于天津市大气边界层观测铁塔资料,揭示了研究时段内颗粒物质量浓度随高度变化的非一致性.近地层是地气之间最邻近的区域,不同气象条件下该区域湍流场结构差异很大,
由此必然会对其间物质和能量的垂直交换产生显著影响,从而导致在大气边界层低层颗粒物质量浓度廓线的复杂性.已有研究表明,大气消光的主体是颗粒物的消光,其水平的高低直接反映了大气环境质量的优劣[8-10].近年来,随着Mie散射激光雷达的广泛应用,由其反演的大气消光系数廓线为边界层颗粒物垂直分布的深入研究提供了数据支撑[11-12].考虑到地球重力的作用,数值模式中通常假定气溶胶含量随高度满足负指数递减,并由此引入了目前通用的大气消光系数垂直分布负指数模型[13-14].基于近年来的观测事实发现,在雾霾发生的静稳气象条件下,负指数模型并不能全面反映颗粒物在近地层附近的垂直分布特征
[15].针对气溶胶含量随高度变化的复杂性,朱育雷等[16-17]利用成都市Mie散射激光雷达探测的资料,通过对近地层以上大气消光系数的系统分析和总结,指出 Logistic曲线能更好地表征大气消光系数在边界层内的垂直演变形态,据此提出了基于 Logistic曲线识别混合层高度的新方法,并在MODIS卫星AOD反演近地面“湿”消光系数中得到了验证.
大气消光系数廓线本质上是颗粒物质量浓度垂直分布的表征,是地气之间热力和动力综合作用的结果.正确构建大气消光系数廓线数学模型是对大气边界层结构复杂性认知的升华,并在卫星 AOD垂直分布订正以及大气环境容量计算等方面具有重要的应用价值[18-20].为此,本文在提出了大气消光系数垂直分布 Logistic模型及其参数计算方法的基础上,系统比对了 Logistic模型和负指数模型在不同稳定度条件下对大气消光系数垂直分布的模拟能力,以期为后续的相关研究和应用提供借鉴.
1 仪器和数据
使用的资料包括成都市2013年6月~2014年5月期间Mie散射激光雷达探测数据、CE-318观测的大气光学厚度(AOD)资料、大气能见度以及地面常规气象观测资料,具体说明如下:
(1)Mie散射激光雷达为北京怡孚和融科技有限公司生产的EV-lidar激光雷达,设置于西南交通大学九里堤校区土木馆(104.06°E,30.70°N)楼顶,距地高度35m,数据采集频率为 1次/3min,主要观测范围可达30km,探测盲区为60m,测距分辨率为15m.
(2)AOD观测仪器为全自动太阳光度计CE-318,来源于成都大气成分站(104.02°E,30.39°N),数据采集频率为1次/h,滤光波长为440,670,870和1020nm,半波宽度为10nm.
(3)大气能见度资料通过Belfort6000型大气能见度传感器获取,监测点位于成都市人民南路环境监测站点(104.07°E,30.63°N),数据采集频率为 1 次/h,精度为±10%.
(4)地面常规气象观测资料由成都市温江气象站(103.83°E,30.70°N)观测,数据采集频率为 4 次/d,主要包含气温、总云量、低云量和风速等气象要素.
以上数据的监测点位两两距离均不超过 20km,环境气象条件基本一致,监测数据在一定误差范围内具有可替代性.
2 大气消光系数垂直分布模型
2.1 大气消光系数垂直分布 Logistic模型及其参数计算方法
大气消光系数垂直分布 Logistic模型的数学表达式为

式中:z和)(zσ分别为高度和其对应的大气消光系数;α、β、γ为大气消光系数垂直分布Logistic模型的参数.
以AOD、混合层高度及地面消光系数作为约束条件,大气消光系数垂直分布 Logistic模型的参数计算方法如下.
记AOD的值为aτ,为大气消光系数在垂直方向上的积分,即

混合层顶是湍流特征不连续界面所在高度,对应于Logistic曲线的曲率最大点[16].进一步利用文献[16]识别混合层高度,记为H,由此得到式(3).

大气消光系数与大气能见度之间满足Koschmieder’s公式[21],通过该公式反演的近地面大气消光系数为σ(0),见式(4).

利用式(2)、式(3)、式(4)求解模型参数α、β、γ,据此提出大气消光系数垂直分布 Logistic模型的参数计算方法.
2.2 大气消光系数垂直分布负指数模型
消光系数是由大气中气溶胶粒子数目和消光截面两个因子共同确定的,其中消光截面与粒子类型、尺度和波长有关,若气溶胶组份和谱分布不随高度发生改变[22],消光截面随高度z也不发生变化,由此得到式(5).

式中:(0)σ和()zσ符号的意义同前;某一高度和近地面的气溶胶浓度分别记为()zN 和(0)N .
假定在地球重力的作用下气溶胶密度随高度呈负指数递减,见式(6).

式中:Ha表示大气标高,km,可近似用边界层高度加以替代.根据公式(5)和(6),由此得到目前普遍应用的大气消光垂直分布负指数模型[14],其函数表达式见式(7).
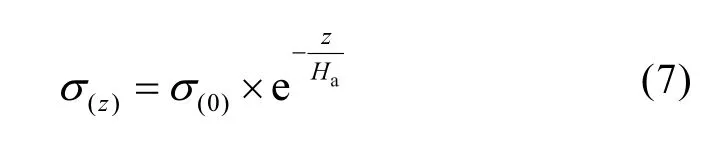
3 大气消光系数垂直分布模型的适用性分析
诸多研究表明,虽然污染物的过量排放是造成大气污染的内因,但污染物浓度的变化乃至重要污染事件的发生均与大气稳定度的演变密切相关[23].当大气层结处于不稳定状态时,从贴地层向上的大气湍流活动强烈,有利于颗粒物的垂直散布;当大气层结处于稳定状态时,颗粒物的垂直扩散则会受到抑制,容易造成污染物的大量积累.大气稳定度是大气层结动力因子和热力因子的综合表征,是描述大气湍流状态和扩散能力的重要指标,稳定度的改变会带来颗粒物垂直结构的相应变化.本文基于成都市 2013年 6月~2014年 5月期间温江站的气象观测数据,利用Pasquill大气稳定度分类方法选取不稳定、中性、稳定3类样本各3个(表1).基于表1给出的相关资料,利用式(1)、式(2)、式(3)、和式(4)求解待定参数α、β、γ,据此得到不同稳定度条件下大气消光系数 Logistic廓线,如图1所示.可见大气消光系数在混合层顶附近自下而上均历经急剧下降区、缓变区以及近似不变区,这与实测的大气消光垂直分布形态完全吻合.同样基于表1给出的相关资料,利用式(7)得到3类稳定度条件下的大气消光系数负指数廓线,如图1所示.为了对比两类大气消光系数垂直分布模型的模拟效果,结合气溶胶的垂直分布范围,表1进一步给出了不同环境气象条件下边界层内实测消光系数和模型计算结果之间的相关系数(R2).由表 1可见,在不稳定和中性层结条件下,Logistic模型计算的大气消光系数与对应实测值之间的平均相关系数(R2)分别为 0.87和0.86,负指数模型计算的大气消光系数与对应实测值的平均相关系数(R2)分别为 0.87和 0.86,均通过a=0.01的显著性检验.因此,在大气垂直扩散能力中等或较好的条件下,Logistic模型和目前通用的负指数模型对大气消光系数垂直分布的模拟效果总体相当.在稳定条件下,Logistic模型计算的大气消光系数与对应实测值之间的平均相关系数(R2)为 0.84,这与稳定和中性层结条件下的结果基本一致;而负指数模型计算的边界层内大气消光系数与对应实测值的平均相关系数(R2)为 0.74,虽然也通过a=0.01的显著性检验,但模拟能力相比于前者出现了明显的降低.上述分析表明,就对边界层内大气消光系数的模拟效果而言,Logistic模型具备更优的适用性.
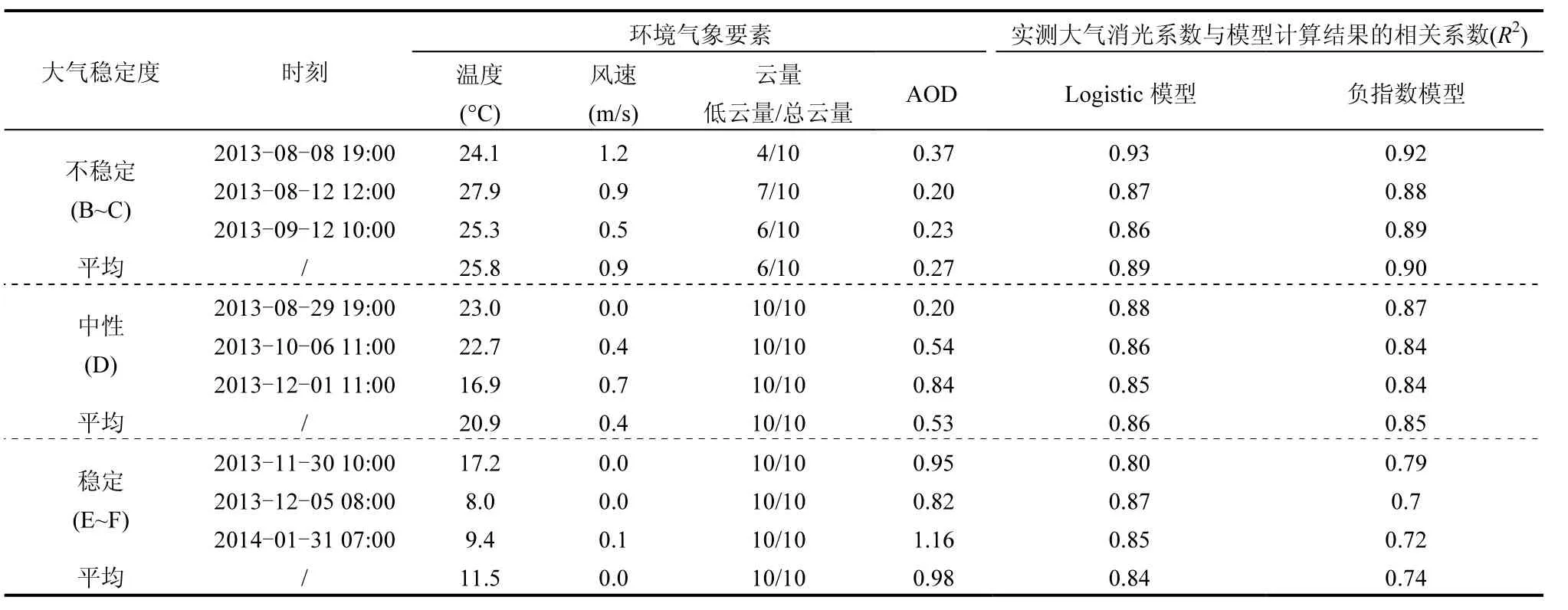
表1 不同环境气象条件下边界层内实测大气消光系数与模型计算结果的相关性Table 1 Correlation between measured atmospheric extinction coefficient and model calculated results in the boundary layer under different environmental meteorological conditions
为分析 Logistic模型和负指数模型对大气消光系数的模拟效果,记实测的大气消光系数和模型模拟的大气消光系数分别为mσ、sσ,以误差平方和(SSE)以及相对误差(δ)为判别依据,对图1中两种模型模拟效果加以分析,其中SSE表达式如下,

考虑到在不同环境气象条件下大气消光系数在近地层附近的差异,进一步提出如下相对误差的计算公式,

式中:σm_max为实测大气消光系数的最大值.
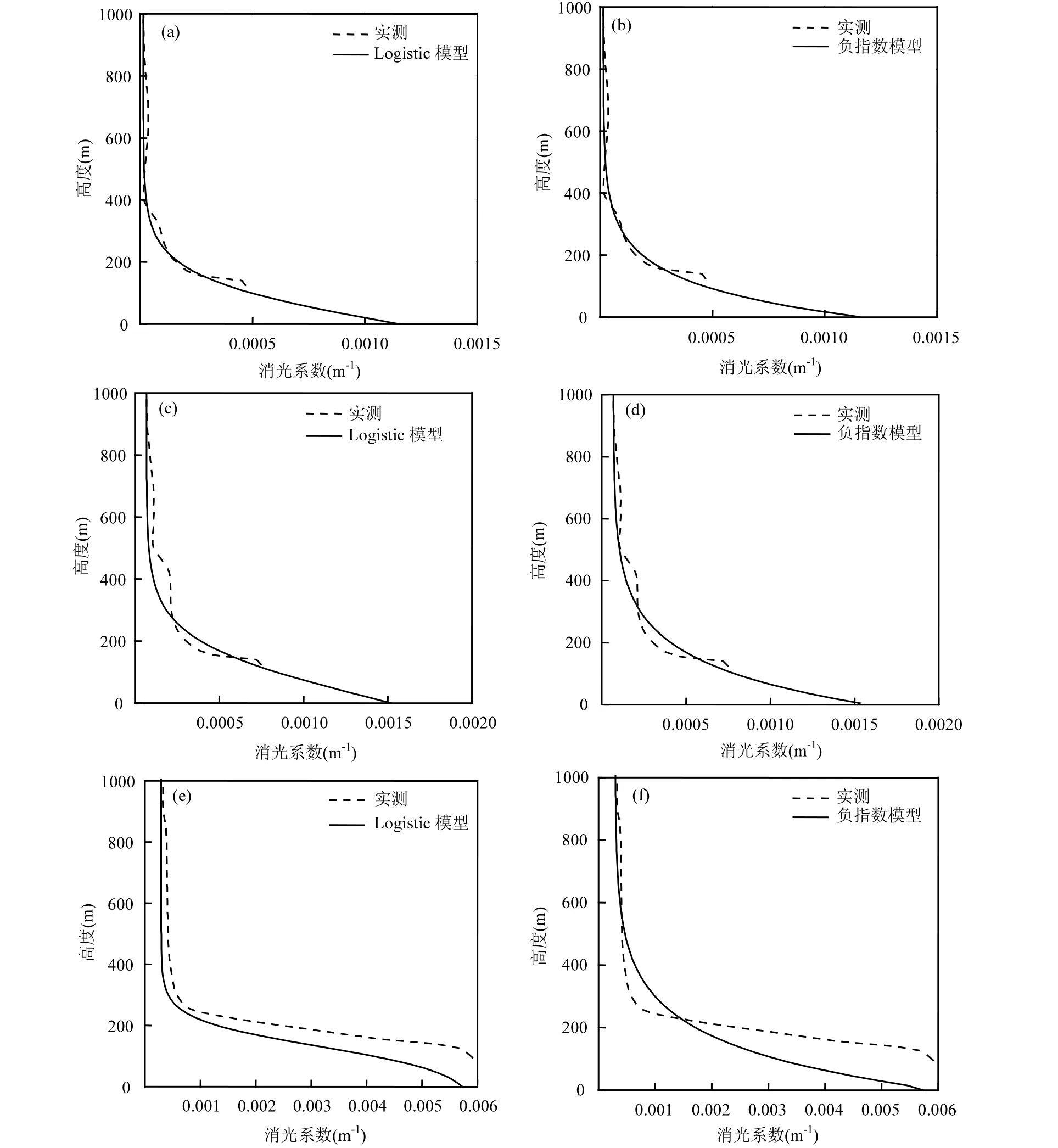
图1 不同大气稳定度条件下实测和模型计算的大气消光系数廓线Fig.1 Comparison of the atmospheric extinction coefficient profiles of measurement and model calculation in different stabilities
基于大气消光系数垂直分布 Logistic模型和负指数模型的计算结果,结合Mie散射激光雷达探测的大气消光系数,利用式(8)和式(9)分别计算表1中3类代表样本在混合层以下误差平方以及相对误差随高度的变化,如表 2所示.统计表明:(1)从不稳定到稳定状态,实测消光系数与两种模型计算结果的误差平方和(SSE)以及平均相对误差()均表现出增大的趋势;(2)不稳定和中性条件下,实测大气消光系数与Logistic和负指数模型计算结果的误差平方和(SSE)以及平均相对误差()总体相当,稳定条件下,Logistic模型相较于负指数模型而言,误差平方和(SSE)以及平均相对误差()显著降低,这与图1是完全一致的.
综上分析不难发现,负指数模型模拟的大气消光系数自下而上均呈现出先快速后慢速的递减形态,这仅与不稳定或中性条件下颗粒物质量浓度的垂直分布保持一致[24-25].随着大气稳定度的增加,湍流场的输送能力渐进减弱,颗粒物的垂直分布形态会出现显著改变[15];基于北京和天津铁塔观测资料的相关诊断结果一致表明,稳定层结条件下的颗粒物在近地层内随高度的降幅是很小的,细颗粒物的变化则更小[26-27];另外,在四川盆地秋冬季节特殊的静稳天气背景下,垂直方向往往存在多重逆温,其中以贴地逆温出现的频率最高和强度最大,这又进一步增加了颗粒物垂直分布形态的复杂程度[28].因此,负指数模型不能全面地模拟大气消光系数垂直分布特征,尤其是在稳定大气条件下的计算结果可能会出现较大偏差.由图1可见,随着参数取值的变化,Logistic模型计算的大气消光系廓线则表现出与稳定度密切相关的凸凹特征,不仅具备负指数模型在稳定和中性大气条件下对大气消光系数垂直分布的良好模拟能力,又能准确表征在稳定条件下颗粒物在近地层缓慢递减的形态,这已得到诸多观测和应用的验证[17].从这个意义上讲,大气消光系数垂直分布Logistic模型的适用性主要在于其不同参数组合可以产生丰富的曲线形态,这为更好地模拟近地层大气消光系数垂直变化的复杂性提供了可能.因此,相比于大气消光系数垂直分布负指数模型,Logistic模型能全面地表征不同大气稳定度条件下的大气消光系数廓线,具有更优的适用性.

表2 实测大气消光系数与两种模型计算结果的误差分析Table 2 Error analyses of measured extinction coefficient and model calculated results
4 结论
4.1 基于 Logistic曲线识别混合层高度新方法的研究成果,结合太阳光度计(CE-318)观测的大气光学厚度(AOD)资料以及近地面能见度数据,提出了大气消光系数垂直分布Logistic模型及其参数计算方法.
4.2 针对成都市2013年6月~2014年5月期间的实例应用结果表明,在不稳定和中性层结条件下,Logistic模型和目前通用的负指数模型对大气消光系数垂直分布的模拟效果总体相当,两模型分别模拟的大气消光廓线与实测的大气消光廓线之间的平均相关系数(R2)均为0.87和0.86;但在持续稳定层结条件下,Logistic模型的模拟效果则显著占优,Logistic模型模拟的大气消光廓线与实测的大气消光廓线之间的平均相关系数(R2)为 0.84,而负指数模拟的则为0.74.
4.3 不同稳定度条件下湍流场结构的差异决定了颗粒物质量浓度在大气边界层低层分布的非一致性,大气消光系数 Logistic模型更优的适用性主要在于其对近地层大气消光的复杂垂直形态具有良好的模拟能力.
