先进多孔径视宁度廓线仪数值模拟研究∗

杨峰 赵刚 任德清

(1 中国科学院国家天文台南京天文光学技术研究所南京210042)

(2 中国科学院天文光学技术重点实验室南京210042)

(3 中国科学院大学北京100049)

(4 Physics & Astronomy Department, California State University Northridge,Northridge, CA 91330-8268)

1 引言

大气湍流廓线用于描述不同高度的湍流强度, 对其进行准确测量对于多层共轭自适应光学系统[1](MCAO)、地表层自适应光学系统[2](GLAO)、断层扫描自适应光学系统[3](TAO)的设计及太阳望远镜的选址具有重要的意义.用于欧洲太阳望远镜(EST)的MCAO系统需要结合大气湍流廓线的详细信息对变形镜数目、共轭高度、单元数等参数进行优化设计[4], 以达到最好的校正效果.

现今有很多方法用于测量大气湍流廓线, 主要分为两类: 基于探测图像闪烁的方法和基于斜率测量的方法.基于探测图像闪烁的方法一般用于夜间湍流廓线的测量,主要有MASS[5](Multi-Aperture Scintillation Sensor)、LuSci[6](Lunar Scintillation)、SCIDAR[7](SCIntillation Detection And Ranging)等.其中, MASS使用探测器测量望远镜光瞳上4个同心圆区域的单个恒星的闪烁, 可以得到低分辨率的湍流廓线; LuSci通过测量月球的闪烁来探测地面层的大气湍流特性; SCIDAR通过观测双星目标, 在探测器上获得两个角度的瞳面图像, 通过对两个图像进行互相关分析, 获得高分辨率的湍流廓线信息.对于日间湍流廓线测量, 基于探测图像闪烁的方法只适用于探测接近地面层的湍流.Beckers[8]设计了SHABAR (SHAdow BAnd Ranging), 利用线性排列的小型探测器测量太阳日面的亮度, 通过计算不同探测器的闪烁变化的相关, 得到大气湍流廓线,该方法的最大探测高度只有500 m.基于斜率测量的方法主要包括SLODAR[9](SLOpe Detection And Ranging)及S-DIMM+[10](Solar Differential Image Motion Monitor +).SLODAR方法通过探测双星的波前相位畸变的局部梯度并进行互相关计算, 可以得到大气湍流廓线, 主要用于夜间湍流廓线测量.S-DIMM+采用和SLODAR类似的原理, 利用不同区域的太阳表面米粒图像探测波前, 可以探测高达30 km的日间大气湍流廓线.S-DIMM+在日间湍流廓线测量中得到了广泛应用, Kellerer等[11]使用该方法获得了大熊湖台址的日间湍流廓线, Wang等[12]对S-DIMM+方法进行了改进, 使用3颗导星进行计算, 测量得到了抚仙湖太阳观测基地的湍流廓线信息.

S-DIMM+的限制在于其必须使用大型望远镜进行测量.2015年, Ren等[13]提出了多孔径视宁度廓线仪(Multiple-Aperture Seeing Profiler, MASP)的概念.MASP由两个约400 mm口径的小型望远镜组成, 可以在没有大型望远镜的台址使用.每个望远镜的后面都配有宽视场夏克哈特曼波前传感器(SHWFS), 使用和S-DIMM+类似的算法进行湍流廓线测量, 可以获得最大探测高度为30 km的湍流廓线数据, 与1 m太阳望远镜上的S-DIMM+测量仪探测能力类似.Yang等[14]对MASP方法进行了改进, 通过使用多颗导星, 提升了MASP测量仪的等效口径, 在增加了其探测能力的同时也提升了S-DIMM+仪器的便携性.

2016年, Ren和Zhao在MASP基础上进行了改进, 提出了先进多孔径视宁度廓线仪A-MASP[15](Advanced Multiple Aperture Seeing Profiler).A-MASP仅使用两个约100 mm口径的小型望远镜, 使用多颗导星进行观测, 且不需要使用夏克哈特曼波前传感器, 这就使得光路更加简单, 且仪器更加便携.Ren等[16]在美国国家太阳天文台的邓恩太阳望远镜上对A-MASP方法进行了验证, 实验使用单个大孔径望远镜加上孔径遮挡以产生两个子孔径, 使用太阳表面的子区域作为等效导星进行计算, 得到了2017年7月12—14日的台址湍流廓线, 结果显示邓恩太阳望远镜台址有3个主要的湍流层, 其中最强的是接近地面的混合湍流层, 另外还有一个接近3 km的湍流层及一个高度为8–15 km、位于对流层顶的湍流层.观测结果表明A-MASP可以成功对日间湍流廓线进行测量.

在MASP和A-MASP中, 需要使用两个望远镜分别对太阳表面进行成像, 望远镜抖动引起的指向误差会对测量结果造成很大的偏差.Ren等[13]在MASP的研究中提出在湍流廓线求解方程中引入消除抖动项, 对湍流廓线求解方程进行改进.同样, 这一方法也可以应用在A-MASP中.然而在A-MASP中由望远镜抖动造成的图像偏移和地表0高度大气湍流造成的偏移在性质上相同, 因此在消除抖动的同时也会使得无法进行地表大气湍流的有效测量.Ren等[15]在A-MASP的研究中没有讨论望远镜抖动和消除抖动公式的影响.本文将延续Ren等[15]在2016年的工作, 使用蒙特卡洛数值模拟方法对A-MASP测量仪应用抖动消除公式进行研究.我们使用100层相位屏对真实大气湍流进行建模, 相比同类的研究普遍使用10–20层相位屏[12,15], 可以更准确地还原对真实大气的探测结果.论文的结构安排如下: 第2节中, 我们简要介绍了A-MASP测量的原理; 第3节中给出了我们的模拟结果, 3.1节中我们使用单层大气湍流模拟, 发现A-MASP中两台小望远镜间距为0.4 m时, 无法测量高度小于0.4 km的湍流, 3.2节中我们提出了A-MASP非均匀采样造成湍流廓线失真的修正方法, 并使用数值模拟进行了验证, 3.3节中我们使用100层相位屏对真实大气进行了建模, 研究了望远镜间距对A-MASP湍流廓线探测能力的影响; 第4节中, 我们首先使用数值模拟的方法对S-DIMM+和A-MASP的恢复结果进行了比较, 然后对全文进行了总结, 并给出结论.

2 A-MASP原理及湍流恢复算法

2.1 A-MASP原理

Ren和Zhao于2016年提出了先进多孔径视宁度廓线仪A-MASP[15], 使用有一定距离的两个小型望远镜的组合测量日间湍流廓线, 每个小型望远镜的直径约为100 mm, 望远镜后面不配备SHWFS, 使用太阳米粒结构中的一个小区域作为导星, 导星的典型尺寸介于8′′×8′′–10′′×10′′之间.A-MASP和S-DIMM+原理类似, 均使用三角测量的方法进行湍流廓线的测量, 不同的是, S-DIMM+使用多组不同距离的子孔径对进行三角测量, 而A-MASP使用多颗导星进行测量.图1为A-MASP的原理示意图, 两个小望远镜的间距为s, 蓝色光线和绿色光线分别表示到达第1个望远镜和第2个望远镜的不同导星的光线, 其中θ为相邻两个导星之间的角间距.我们可以看到蓝色光线和绿色光线在s/4θ、s/3θ、s/2θ和s/θ等高度相交, 根据三角测量原理可以测得相应高度的湍流强度.在具体计算中, 首先通过计算求得不同导星偏移量的协方差, 之后通过恢复算法, 求得不同高度的Fried参数, 最后获得湍流廓线.

图1 先进视宁度廓线仪原理图Fig.1 Schematic of the Advanced Multiple Aperture Seeing Profiler

2.2 湍流恢复算法

A-MASP使用两个望远镜同时进行观测, 存在指向误差的问题.Ren等[13]提出了一组新的方程, 可以消除两个望远镜之间的相对位置偏移.我们在观测图像上沿x方向(两个望远镜连线方向)划分一系列均匀排列的小区域作为导星, 并计算导星相对位移的偏移量:

其中δxi为第i颗导星在x方向的偏移量,δyi为在相应y方向的偏移量,NL为采样层数,cn为待求系数, 该系数与Fried参数相关,s为两台望远镜之间的距离, ∆x和∆y用于移除两个望远镜x和y方向的相对位置偏移,⟨⟩表示对多次测量的平均.θij为第i颗导星和第j颗导星的夹角, 不妨设j>i, 可表示为θij=(j −i)θ,θ为相邻两颗导星之间的夹角,hn为第n层采样高度.式中Fx和Fy是大气结构函数I(u,0)和I(u,π/2)的组合, 其中u为以望远镜口径归一化后的距离, 第2项0和π/2分别表示x方向和y方向, 其表达式为:

其中Deff为有效直径, 可以表示为Deff=D+φhn, 此处,D为望远镜口径,φ是视场的平均直径.我们使用圆形孔径, 根据Kellerer的文章[17], 大气结构函数I(u,0)和I(u,π/2)可以表示为:

其中w=1+1.14u−5.5/3.(1)式中, ∆x和∆y用于移除两个望远镜x和y方向的相对位置偏移, 可以表示为:

∆x和∆y的推导过程参见Ren等[13]在2015年的工作, 通过(1)式, 可以解出系数cn, 它与相应层的Fried参数r0的关系为:

在(1)式和(2)式中, 如果取h1=0, 表示地面处的湍流层.我们有c1F(s,θ,h1)=c1I(s/Deff,0), 与∆中相关的项抵消, 即式子中不含c1项.也就是说, 在A-MASP中, 接近地面0高度的湍流层无法通过消除抖动的方程解出.这是A-MASP方法的局限性.然而,我们使用其他的设备如日间DIMM获得全局Fried参数, 可以计算出湍流层高度h=0时的cn值.

3 湍流廓线恢复数值仿真

我们应用蒙特卡罗数值仿真方法研究湍流廓线恢复过程, 与Ren等[13]使用的方法类似.具体过程如下:

(1)利用Johansson和Gavel[18]给出的方法, 获得每一层湍流层对应的Kolmogorov相位屏;

(2)将两个望远镜孔径沿导星的方向投影到不同高度的湍流层相位屏上, 截取相应的子区域.为了节省计算时间, 我们在模拟中使用点目标代替扩展目标作近似;

(3)将导星对应的不同层高的相位屏子区域叠加, 并使用快速傅里叶变换求得每个导星的点扩散函数(PSF), 利用重心法求出PSF的偏移量;

(4)代入(1)式, 计算等号左侧x,y方向偏移量的协方差;

(5)选择采样高度hn, 并使用非负最小二乘法求解方程, 得到hn高度对应的系数cn,通过(5)式计算湍流层的r0.

在本文的研究中, 我们模拟望远镜的直径D=0.12 m, 导星的数量N=12颗.这些导星沿两个望远镜的连线方向(x方向)均匀排成一列, 相邻导星的角距离为θ=8′′.对于每组算例, 我们模拟了1000幅观测图像对应的偏移量.

3.1 单层大气湍流恢复仿真

为了研究消除抖动项对湍流廓线计算的影响, 我们首先使用单层大气进行湍流廓线恢复过程的仿真研究.我们进行了75组模拟, 在模拟中单层大气湍流的高度分布在0–15 km之间, 高度间距均为200 m,r0均设为0.1 m.两台望远镜的距离为s=0.4 m.在求解中, 采样高度设为和模拟的大气湍流层高度相同.图2为湍流强度恢复的结果, 其中黑色水平点线为输入的r0=0.1 m, 实线为通过模拟恢复得到的r0值, 线上的每个圆点代表一组模拟的结果.从图中我们可以看出, 对于单层大气, 湍流强度恢复的偏差大约为2%, 这表明我们的模拟和计算过程都是正确的.根据之前的分析, 我们已经知道使用A-MASP无法解出高度为0的湍流层强度.从图中我们还可以看到, 对于高度较低的湍流层(h0.4 km), 使用消除抖动的公式解算出的r0同样具有较大的偏差.

3.2 采样点等效高度计算

在A-MASP湍流廓线测量中, 我们需要选择多个采样高度, 用来计算采样点处的等效湍流强度.对于N颗导星的情况, 我们根据A-MASP中使用的三角测量的原理, 选择N −1个采样高度,hn=s/θN−n, 其中θN−n=(N −n)θ, 代表了对应的导星之间的角距离,θ为相邻导星之间的夹角.h1对应最低采样高度为h1=s/θN−1.显然, 我们可以看出采样高度的分布是非均匀的, 在较低的高度采样较密集, 在较高的高度采样较稀疏, 这可能会导致计算得到的湍流廓线出现失真.

图2 使用单层大气得到的湍流强度恢复结果Fig.2 Retrieved results of the atmospheric turbulence strength using a single layer atmosphere

根据Scharmer和van Werkhoven的文章[10], 当湍流层位于两个采样高度之间, 会同时影响两个采样高度计算得到的等效湍流强度值.距离采样高度越近, 则对其影响越大.为了分析的方便, 我们近似认为两个采样高度之间的湍流层仅影响较近的采样高度.如果采用了这个假设, 采样高度hn实际上测量的是hn−1到hn的中点和hn到hn+1的中点,即s/(2θN−n+1)+s/(2θN−n)到s/(2θN−n)+s/(2θN−n−1)的这一段高度的总的湍流廓线强度.使用这一段高度的中点s/(4θN−n+1)+s/(2θN−n)+s/(4θN−n−1)作为等效高度得到的等效湍流廓线强度更为合理.

为了验证上面的分析, 我们使用12层大气湍流层模型进行验证.这12层湍流高度分布在0–17.6 km, 相邻两层之间的间距为1.6 km, 每一层的输入r0=0.1 m.导星数目N=12, 相邻导星的角间距θ=8′′, 望远镜口径D=0.12 m.我们计算了3组算例, 其中望远镜之间的间距s分别设置为0.4 m、1.2 m和2.0 m.湍流廓线恢复的结果如图3所示, 其中横坐标为高度, 纵坐标为累积湍流廓线强度, 即低于对应高度湍流强度的总和.黑色台阶状点线是输入的累积湍流廓线强度.带有圆形数据点的虚线和方形数据点的实线分别表示了直接采用采样高度hn和使用等效高度s/(4θN−n+1)+s/(2θN−n)+s/(4θN−n−1)计算得到的累积湍流廓线.3个子图分别表示望远镜间距为0.4 m、1.2 m和2.0 m时得到的结果.从图中可以明显看出, 对于3个算例, 使用等效高度时恢复的湍流廓线能够和输入的吻合得更好, 这表明我们对于采样点等效高度的分析是合理的.

以上分析并非只可以用在A-MASP测量中, 在湍流廓线测量中, 由于高层大气湍流较弱而底层较强, 因此经常采用非均匀的采样高度, 即在较低高度使用较多采样点, 在较高高度使用较少采样点(例如Scharmer和van Werkhoven的文章[10]), 在这种情况中, 采用等效采样高度更为合理.另外, 在上面的分析中, 我们假设湍流层只影响较近的那个采样高度, 在今后的工作中, 我们将建立不同湍流层的影响函数, 进行更精确的分析.

图3 使用12层大气得到的湍流廓线恢复结果, dh表示湍流廓线强度, 黑色台阶状点线为输入的累积湍流廓线强度,3幅图分别表示望远镜的间距为0.4 m、1.2 m、2.0 m时的恢复结果.Fig.3 Retrieved results of the atmospheric turbulence profile using 12 layers’ atmosphere, C2ndh represents the intensity of turbulence profile, the black step-like dotted line is the input cumulative strength of turbulence profile, three panels represent the recovery results of the telescope with the spacing of 0.4 m, 1.2 m, and 2.0 m, respectively.

3.3 使用HVB模型进行湍流恢复

为了能更真实地模拟大气湍流廓线, 我们使用Hufnagel-Valley-boundary (HVB)模型[19]对湍流廓线进行模拟.HVB模型在夜间大气常用的Hufnagel-Valley模型基础上, 考虑了描述日间大气边界层的影响, 可以反映日间大气湍流的分布特点.在HVB模型中,日间湍流廓线可以表示为

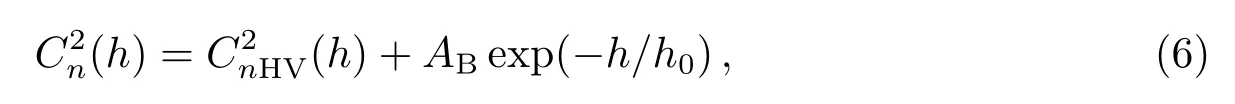
其中方程右边的第1部分是Hufnagel-Valley模型, 主要用于计算夜间湍流廓线, 可以表示为[3]

其中AHV是HV模型强度,z是台址的海拔高度.(6)式中第2部分表示由日间地面边界层引起的额外湍流, 其中AB为边界层的强度,h0是边界层的高度.

设定海拔高度为z=3000 m, 边界层高度为h0=640 m, 边界层强度为AB=1×10−7, 强度AHV为0.245.我们使用100层湍流模拟HVB模型.这100层湍流分布在0–20 km 高度, 间隔为200 m, 每层的湍流强度通过HVB模型计算得到.图4中点线表示输入的累积湍流廓线强度.在模拟中, 导星数目N=12, 相邻导星的间距为θ=8′′, 两个望远镜的口径均为D=0.12 m, 望远镜之间的间距分别设置为0.4 m, 1.2 m和2.0 m.图4给出了这3个算例的湍流廓线恢复结果.带有圆点的实线为望远镜间距为0.4 m时的结果, 从图中可以看到, 对于5 km以下的湍流, 我们恢复计算得到的累积湍流廓线和输入的湍流廓线有非常相似的形状, 这表明对于5 km以下的湍流可以进行较好的恢复.由于0高度附近的湍流无法计算, 恢复得到的湍流廓线和输入值之间总强度约有0.6×10−13m1/3的差距, 这个差距和HVB模型中h0.4 km前3层强度的和非常接近,这和我们3.1节的结果吻合, 进一步说明当s=0.4 m时, 无法对0.4 km及以下的湍流层进行测量.当高度大于5 km时, 由于采样不足, 模拟恢复得到的湍流廓线不能反映输入湍流廓线的形状, 仅可以对其总强度进行估计.

图4 使用HVB模型得到的湍流廓线恢复结果, dh表示湍流廓线强度, 黑色点线为输入累积湍流廓线强度.Fig.4 Retrieved results of the atmospheric turbulence profile using the Hufnagel-Valley-boundary model,dh represents the intensity of turbulence profile, the black dotted line is the input cumulative strength of turbulence profile.

对于望远镜间距为1.2 m和2.0 m的算例, 图4中的带有方点的虚线和带有三角点的虚线给出了恢复的结果.可以看出在这两种情况下, 对于5 km之下的湍流廓线, 由于A-MASP的限制, 恢复结果与输入值符合得较差.而对于5 km以上的湍流廓线形状符合得较好.对于所有3种情况, 最后总的湍流强度值都低于输入值, 这主要是由AMASP无法获得0高度附近的湍流强度导致的.在实际的湍流廓线测量中, 我们可以通过日间DIMM等方法获得总的湍流强度, 并对A-MASP恢复结果进行修正.另外, 在实际的大气湍流廓线测量中, 我们可以通过改变望远镜间距来对整个范围内的大气湍流进行更准确的测量.

4 讨论和结论

4.1 讨论

S-DIMM+方法是目前日间光学湍流廓线测量中使用最广泛的方法.我们计划通过在已建成的太阳望远镜上搭建S-DIMM+, 与A-MASP进行联合测量, 对A-MASP仪器性能进行验证.为确保联合测量的顺利进行, 我们首先使用数值模拟的方法对S-DIMM+和A-MASP的探测结果进行比较.其中S-DIMM+仪器搭建在1 m太阳望远镜上, 具有14个方形子孔径, 每个子孔径尺寸为8 mm, 使用太阳表面的两个小区域作为导星, 导星的角距离为11′′.A-MASP中两台望远镜口径均为0.12 m, 间距为0.4 m.图5给出了数值模拟的结果, 图中的点线为输入的累积湍流廓线强度; 虚线为模拟得到的S-DIMM+测量结果; 实线为A-MASP的模拟测量结果.由于A-MASP仪器无法测量h0.4 km的大气湍流, 为了使结果更为直观, 我们人为将A-MASP的测量结果增加0.6×10−13m1/3.从图中可以看出, 在1 m望远镜上的S-DIMM+的测量结果精度较高, 与输入的湍流廓线符合得非常好, 因此可以作为参考对A-MASP仪器探测结果进行验证.S-DIMM+的采样高度分布均匀, 在测量范围内具有一致的垂直分辨率, 而A-MASP由于使用多颗导星,在5 km以下的近地面区域具有比S-DIMM+更高的垂直分辨率.我们可以通过比较湍流廓线的大致形状对这一段高度的测量结果进行验证.另外, 如果在S-DIMM+中使用多导星[12,14], 可以进一步提高S-DIMM+在地面附近的湍流廓线测量垂直分辨率, 从而更好地实现相互对比验证.

图5 A-MASP和S-DIMM+湍流廓线恢复结果比较, dh表示湍流廓线强度.Fig.5 Comparison of the retrieved results of atmospheric turbulence profile using A-MASP and S-DIMM+ methods, dh represents the intensity of turbulence profile.

4.2 结论

本文使用数值模拟的方法对多孔径湍流廓线测量仪A-MASP进行了研究.A-MASP使用两个小口径望远镜测量日间湍流廓线.为了消除两台望远镜在观测中由于抖动而产生的指向误差, 在A-MASP相关湍流廓线测量恢复算法中引入了额外的修正项.而该修正项的引入会导致湍流层高度h=0时的大气湍流强度无法测量, 这一效应在之前的文章中尚未进行仔细研究.本文主要结论有:

(1)使用消除抖动的湍流廓线测量公式后, A-MASP对地面附近的湍流不敏感.单层大气湍流模拟和HVB模型大气湍流廓线模拟都显示, 当两台望远镜间距为0.4 m时,A-MASP无法探测高度小于400 m的湍流, 即最低探测高度为400 m.该最低探测高度和A-MASP中小望远镜的距离、口径, 导星的数目、间距都有关系, 在真实观测中可以结合仪器具体的参数, 使用和本文类似的方法进行计算;

(2) A-MASP测量中的采样高度为非均匀分布, 这会导致获得的湍流廓线出现失真.我们提出了等效采样高度的计算方法, 可以对非均匀采样造成的湍流廓线失真进行修正.数值模拟结果表明, 修正后的湍流廓线和输入值吻合得更好.该方法不仅可以应用在A-MASP中, 还可以应用在其他使用非均匀采样的湍流廓线测量(例如S-DIMM+)中;

(3)结合日间湍流廓线HVB模型, 我们使用100层相位屏对20 km以下的日间大气湍流进行了建模, 相比之前工作可以更准确地还原A-MASP仪器对真实日间大气湍流廓线的测量结果.我们发现当两台望远镜距离为0.4 m时, A-MASP可以很好地恢复0.4–5 km的低层大气湍流廓线的形状、强度以及5 km以上大气湍流的总强度.当望远镜间距为1.2 m和2.0 m时, A-MASP可以较好地恢复5 km以上的高层大气湍流廓线的形状.在实际的大气湍流廓线测量中, 我们可以通过改变望远镜间距对整个范围内的大气湍流廓线进行测量.