按比例分配的解题策略

2018-07-26江西省赣州市章贡区沙河镇中心小学康宇斌

数学大世界 2018年17期

江西省赣州市章贡区沙河镇中心小学康宇斌

《按比例分配问题》是人教版小学数学第十一册的内容，是在学生理解了比与分数的联系，已掌握简单分数乘除法应用题数量关系的基础上，把比的知识应用于解决相关的实际问题的一个课例。按比分配是一种分配思想，在生活、生产中是很常见的，已学过的平均分其实是按比分配的一种特例。教学中要通过解决实际生活的问题，让学生了解在生活、生产中常常要把一个数量按照数量的多少来分配。按比例分配解决问题之所以比较难学，是由于问题本身的复杂性，使得很多学生面对问题时无从下手。经过多年的教学，掌握以下几个解题技巧可以熟练应对解决此类问题：

一、掌握基本题型的结构特点

在教学过程之中，教师要加强对学生进行按比例分配问题的结构分析。首先要了解按比例分配问题是把一些东西按照一定的比分给两个或者两个以上的人，一般来说，这些东西的数量是已知的，关键是我们要知道按照什么样的比来进行分配。按比例分配问题的已知条件包括要分配的总数和按照什么样的比来进行分配。基本题型如：学校有1200本课外读物，按2∶3分给五、六年级，每个年级可以分得多少本？

由此可知，学校把1200本课外读物平均分成5份，五年级可分得1200本的，六年级可分得1200本的。

二、学会举一反三，变间接关系为直接关系

加强学生对题目已知条件之间的关系的分析，学会举一反三，然后在分析、总结之中找到解题的思路。有些按比例分配的问题的已知条件中，除了已知总数外，其他几个量的比例关系不直接告知，而是告知这几个量的间接关系，那我们的解题思路就是要求出这几个量的间接比例关系。

如：植树节时，学校组织同学们共植杨树和柳树96棵，已知杨树的和柳树的一样多。同学们植的杨树和柳树各有多少棵？

又如：一个周长为104厘米的长方形，长比宽多，这个长方形的面积是多少平方厘米？

这个长方形的周长是已知的，但长和宽的比是未知的，我们可以利用长和宽的间接关系求出长和宽的比是1+=8∶5，这样就可以再根据按比例分配的基本题型解决。

三、要善于把隐藏的条件找出来为解题所用

有时解决问题，看似所给的题目缺少已知条件，貌似无法解答，其实是题目故意将条件隐藏起来了，没有用数字明确地告知我们。如果我们细心一点，认真读题，找出隐藏的已知条件，就可以解答了。如：一个等腰三角形的底角和顶角的比是1∶4，这个三角形的底角和顶角各是多少度？这个题目隐藏了两个条件，如果审题不仔细会找不出来，一个是内角和180o,另一个则是还有一个底角1份，三个内角的比分别是1∶1∶4，然后再根据按比例分配的基本题型解决。

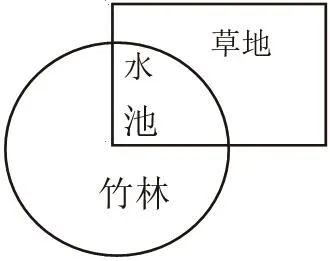
看起来竹林和草地没有直接联系，但仔细观察可以发现水池既是草地的，又是竹林的，从这里我们可以求出草地和竹林的比是5∶14。这样，我们又可以再根据按比例分配的基本题型求出答案。