平行四边形,你找全了吗
2018-07-26浙江省宁波市镇海蛟川书院数学组
浙江省宁波市镇海蛟川书院数学组 滕 丽
纵观近几年中考,有这样一类问题:在平面直角坐标系中,已知一些点的坐标,求可以构成平行四边形的其他点的坐标,若再以抛物线等为背景,加大了题目的综合性,备受中考命题者的青睐。这类问题因为平行四边形的边或对角线的不确定性,需要分类讨论,而考生如果没有弄清分类标准常常会导致漏解。笔者从近几年的中考题中整理出三种类型,与各位同仁交流。
类型1:已知三个定点,找第四个点,使得以这四个点为顶点的四边形是平行四边形
分析:已知三个点A、M、N,求第四个点D,使其构成平行四边形,可以按边进行分类:①以AM、MN为一组邻边,AN为对角线;②以AN、MN为一组邻边,AM为对角线;③以AM、AN为一组邻边, MN为对角线。满足条件的点D的位置可能有如图1所示的三种情形。
解:易得A(0,2),B(4,0),M(2,1),N(2,5)。
当点D在y轴上时,设点D的坐标为(0,a),由AD=MN得|a-2|=4,解得a1=6,a2=-2,从而点D的坐标为(0,6)或(0,-2)。
当点D不在y轴上时,由图可知点D为D1N与D2M的交点。

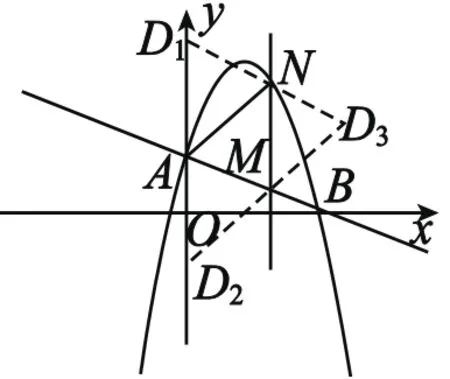
图1
小结:已知三个定点A、B、C,可以确定△ABC,过三个顶点分别作对边的平行线,三条平行线两两相交有三个交点,这三个交点就是平行四边形第四个顶点所在的位置。一般地,如果已知三点坐标A(a1,b1)、B(a2,b2)、C(a3,b3),根据点的平移坐标变化规律,可知以AB、BC为一组邻边的平行四边形的第四个顶点D的坐标为(a1+a3-a2,b1+b3-b2),其他情况同理可得。
类型2:已知两个定点,找两个点,使得这四个点为顶点的四边形是平行四边形
例2 如图2,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C。(1)求抛物线的函数表达式。(2)若点D在抛物线上,点E在抛物线的对称轴上,且以A,O,D,E为顶点的四边形是平行四边形,求点D的坐标。
分析:已知两个定点A,O,分别在抛物线及其对称轴上找两个点D,E,使得构成的四边形为平行四边形,分两种情况讨论:①OA为对角线,D,E关于x轴对称,则点D与点C重合;②OA为平行四边形的一边,则DE∥OA,DE=OA=2。
解:(1)设抛物线的函数表达式为y=ax(x-2)。
∵抛物线过点B(3,3),∴3=3(3-2)a,∴a=1,∴y=x2-2x。
(2)若OA为对角线,∵C(1,-1),则点D的坐标应为(1,-1)。
若OA为平行四边形的一边,则DE=OA=2。
∵点E在抛物线的对称轴上,∴点E的横坐标为1,
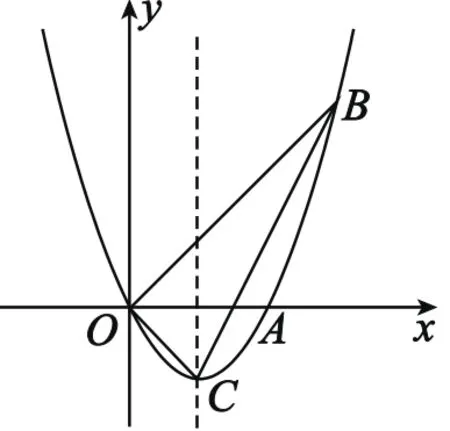
图2
∴点D的横坐标为3或-1,代入y=x2-2x,得D(3,3)或D(-1,3)。
综上所述,点D的坐标为(1,-1)或(3,3)或(-1,3)。
小结:已知两个定点A、B,找两个点C、D,使得以点A、B、C、D为顶点的四边形为平行四边形,这两个点确定线段AB,分别以AB为边或对角线进行分类讨论。一般地,在直角坐标系中,如果平行四边形的顶点坐标是 A(a1,a2),B(b1,b2),C(c1,c2),D(d1,d2),那么有:a1+c1=b1+d1,a2+c2=b2+d2,即相对顶点的横坐标之和相等,相对顶点的纵坐标之和相等。
类型3:已知两个定点,找两个点,使得这四个点为顶点的四边形是菱形
分析:若以O、D、M、N为顶点的四边形是菱形,则△ODM是等腰三角形,分三种情况进行讨论:①当MD、MO为菱形的邻边时,OD是△ODM的底边,点M在OD的垂直平分线上;②当OD、OM为菱形的邻边时,DM为△ODM的底边,点M在以O为圆心,OD长为半径的圆与直线的交点处;③当DO、DM为菱形的邻边时,OM为△ODM的底边,点M在以D为圆心,OD长为半径的圆与直线的交点处。
解:由已知得D(0,5)。
①如图4,当MD=MO时,MN与DO互相垂直平分,点M是DF的中点。
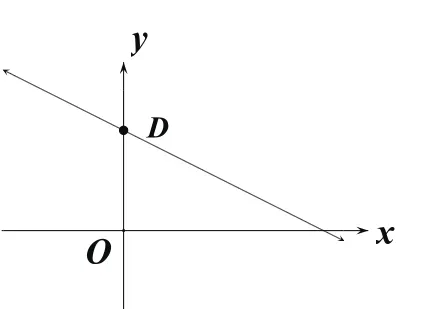
图3
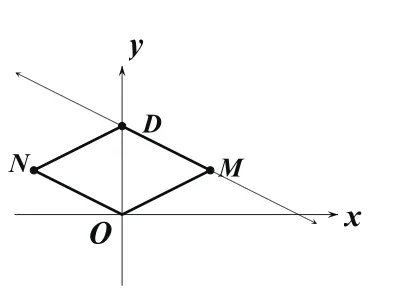
图4

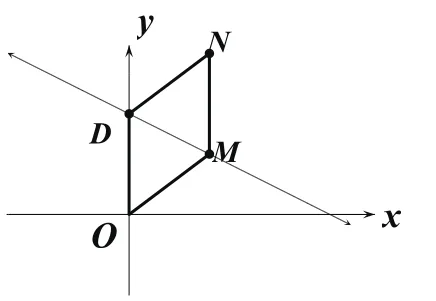
图5
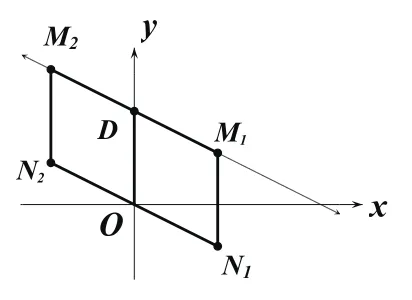
图6
小结:已知两个定点A、B,找两个点C、D,使得以A、B、C、D为顶点的四边形是菱形,分别以AB为底边或腰进行分类,确定第三个点C,使得△ABC是等腰三角形,从而转化成类型1的情形。另外要注意充分利用题目中的平行或相等关系,简化寻找过程。
