风对碟式太阳能聚光器影响的数值模拟研究

王林军， 罗 彬， 张 东， 张跃智， 李亚宁

(1.兰州理工大学 机电工程学院，兰州 730050；2.兰州理工大学 西部能源与环境研究中心，兰州 730050)

碟式太阳能聚光器是碟式太阳能热发电系统中至关重要的部件，其性能对系统的发电效率、稳定性和成本等有很大影响[1]。碟式太阳能聚光器的空间尺寸和迎风面积较大，对外界风载荷作用极为敏感。风载荷作用不仅会造成聚光器镜面变形，还有可能导致聚光器的结构被破坏，使整个系统的发电效率降低。因此，为提高碟式太阳能聚光器的抗风载荷能力和结构强度，对碟式太阳能聚光器进行风载荷方面的研究是非常必要的[2-3]。

工程中结构风载荷的研究方法主要有现场实测、缩尺模型风洞实验和数值模拟风洞等[4]，其中现场实测易受到场地等环境因素的制约，且无法在结构建成前进行相应测试。由于碟式太阳能聚光器空间尺寸大、桁架结构复杂，所以制作缩尺模型存在很大的难度。随着计算流体动力学和计算机技术的发展与完善，数值模拟风洞已成为一种有效的结构风载荷研究方法。

目前，数值模拟风洞主要应用于槽式抛物型聚光器和平板型太阳能电池板等方面。Mier-torrecilla等[5]通过对槽式抛物型聚光器进行数值模拟仿真，发现风载荷仿真结果与风洞实验的结论一致。Hachicha等[6-7]研究了在不同高度角和风速下槽式抛物型聚光器流场特性的变化规律。Lin等[8]通过数值模拟风洞方法，得到了平板光伏电池的风载荷分布，并对光伏机构进行了力学分析，评价了结构抗风的有效性。吴志成[9]研究了气流紊流度对碟状抛物面气动特性的影响，得出气动力载荷的变化规律,能为后续碟状抛物面风载荷模拟提供数据依据。何轶等[10]通过构造准确的有限元模型，采用CFD方法对碟状太阳能聚光器进行数值模拟，得到聚光器碟面各区域的结构系数以及聚光器应力和变形与高度角之间的关系。颜健[11]对复杂碟式机架开展了三维定常风场的数值模拟，并给出聚光器镜面分区的体型系数分布以及风载荷变化规律。Lovegrove等[12]以面积为500 m2的抛物型聚光器为对象，分析了聚光器在不同风载荷作用下的流场分布规律。由于聚光器在结构上存在差异，会导致模拟结果不同，因此现有的相关数据均仅供参考。目前，同时对碟式太阳能聚光器进行风载荷数值模拟和流场特性分析的文献较少，故采用数值模拟方法研究风对碟式太阳能聚光器的影响具有一定的价值。

笔者以碟式太阳能聚光器的三维简化模型为分析对象，基于Fluent 14.0软件并采用Realizablek-ε模型对其进行数值模拟仿真，揭示在不同高度角和方位角下碟式太阳能聚光器碟面风载荷系数的变化规律；对施加在聚光器上的风载荷作用力及力矩进行了研究，并对部分典型工况下碟式太阳能聚光器镜面流场特性进行了分析，得出聚光器在恒定风速下的最差和最佳避风工况，为工程实际中聚光器的抗风设计提供了理论参考。

1 碟式太阳能聚光器模型及网格划分

1.1 碟式太阳能聚光器模型建立

(a) 聚光器简化模型(b) 模型网格划分

图1 碟式太阳能聚光器模型及其网格划分

Fig.1 Model and grid division of the dish solar concentrator

1.2 计算域的确定

为保证空气在流体域内得到充分发展，避免流体域边界对模拟结果产生过大干扰，流体域应足够大，并保证流体域边界与聚光器模型保持一定距离，以尽可能贴近实际风的作用范围。在数值模拟风洞过程中，Baetke等[13]提出用阻塞率S来衡量计算域的尺寸，当S≤3%时可认为计算域是符合要求的。

S=AB/AC

(1)

式中：AC为流体域的横截面积；AB为模型的有效迎风面积，AB取129.667 9 m2，该值是聚光器在0°-0°(高度角-方位角)工况下的有效迎风面积，相比于其他工况，此工况下聚光器的有效迎风面积最大。

确定计算域的尺寸为150 m×80 m×70 m，聚光器模型中心距离进风口为55 m，距离地面高度为10 m，如图2(a)所示。经计算，阻塞率S约为2.31%，说明流体域的尺寸符合要求。

1.3 网格划分

在Gambit软件中进行网格划分，整个流体域采用区域分块和逐级划分的方式，靠近聚光器模型区域的网格较密，远离聚光器模型区域网格的间距逐渐稀疏。为进一步提高网格质量，通过Laplacian光顺方法对网格点进行细微调整，以保证网格的扭曲率不超过0.9，碟面网格划分如图1(b)所示。

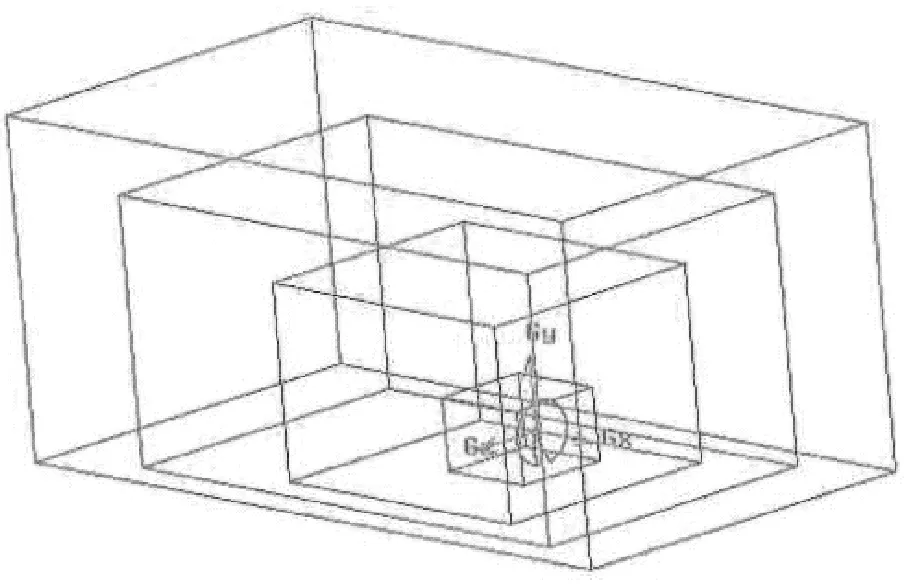
(a) 计算域模型

(b) 计算域网格划分图2 0°-0°工况下计算域模型及其网格划分

Fig.2 Model and grid division of the computational domain in 0°-0° case

图2(b)给出了聚光器在0°-0°工况下流体域的网格划分情况，该工况下网格总数为1 745 229。对于其他工况，划分网格时只需改变聚光器模型相应的角度，同理进行网格划分即可,最后保存为.mesh文件并导入Fluent进行模拟分析。

2 控制方程分析及计算域边界条件设置

2.1 控制方程

流体流动遵守物理守恒定律，其中质量守恒、动量守恒和能量守恒是对任何流体进行分析时需要遵循的三大基本守恒定律，如果用数学语言来描述守恒定律，则称为控制方程[14-15]。流体的流动分为层流和湍流，取决于雷诺数是否超过临界雷诺数。

(2)

式中：V为风速，取值为22 m/s；d为特征长度，取值为13 m；ν为流体的运动黏度，取值为1.79×10-5m2/s。

经计算，雷诺数Re为1.63×107，故整个流体的流动为湍流，层与层之间同时存在质量和动量的传递。

(1) 质量守恒方程。

质量守恒方程是指单位时间内流体微元体中质量的增加等于同一时间流体流入和流出该微元体的质量差[16-17]。根据欧拉法有限体积法，质量守恒方程为：

(3)

式中：ρ为流体密度；u、v和w分别为流体在x、y、z方向的速度分量。

由于流体为不可压缩气体，密度为定值，所以∂ρ/∂t=0，式(3)可表示为：

(4)

(2) 动量守恒方程。

动量守恒方程是指微元体中流体动量对时间的变化率等于微元体受外界所有作用力之和[16]，在x、y和z方向上的动量守恒方程分别为：

(5)

(6)

(7)

式中：p为流体微元体上的压力；τij为作用在微元体表面黏性应力τ的分量，其中i、j分别表示x、y、z；Fi为微元体上的体积力。

由于对聚光器风载荷的数值模拟不涉及热交换问题，可以不考虑能量守恒，所以仅对质量守恒和动量守恒进行描述，在后续Fluent软件中也不对能量进行监控设置。

2.2 计算域边界条件的设置

数值模拟采用的湍流模型为Realizablek-ε，流体材料设为恒定密度的空气，即不可压缩。采用3D单精度、非耦合式求解器和速度压力耦合SIMPLEC算法进行求解，欠松弛因子采用默认值，计算域边界条件具体设置如下。

(1) 入口边界条件：流体为不可压缩的空气，采用速度入口边界条件，可定义计算域进口处流体的速度以及其他相关流动属性。

(2) 出口边界条件：仅需保证出口流场接近完全发展状态，故采用完全发展出流边界条件。

(3) 壁面条件：主要对聚光器表面、背面、侧面和流体域地面进行限制，将其设置为无滑移的壁面条件，将流体域的顶面和左右面设置为对称边界条件，模拟自由滑移壁面。

考虑到计算域的网格数量不多，将迭代步数设置为1 200步，即可保证模拟结果的可靠性与计算的收敛性等。

3 仿真结果与分析

风载荷作用在聚光器上，在聚光器旋转中心处的风力可分解为3个力和3个力矩。图3给出了风载荷各分量与坐标系的关系。

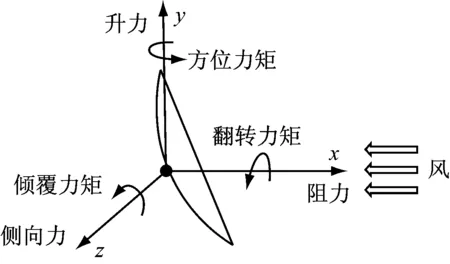
图3 碟式太阳能聚光器镜面的受力情况Fig.3 Force analysis of the concentrator mirror

为便于计算，用风力系数和风力矩系数来表示风载荷在坐标轴上的分力和分力矩。

(8)

(9)

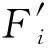
3.1 风载荷系数监控曲线设置

在模拟计算过程中，不仅要监控控制方程的迭代残差量，还要监控相关物理量。当相应的监控曲线不再趋于平稳时，认为计算达到收敛。为保证风向垂直于计算域，图4给出了风力系数和风力矩系数的监控设置，限于文章篇幅，仅给出阻力系数和翻转力矩系数的监控设置。

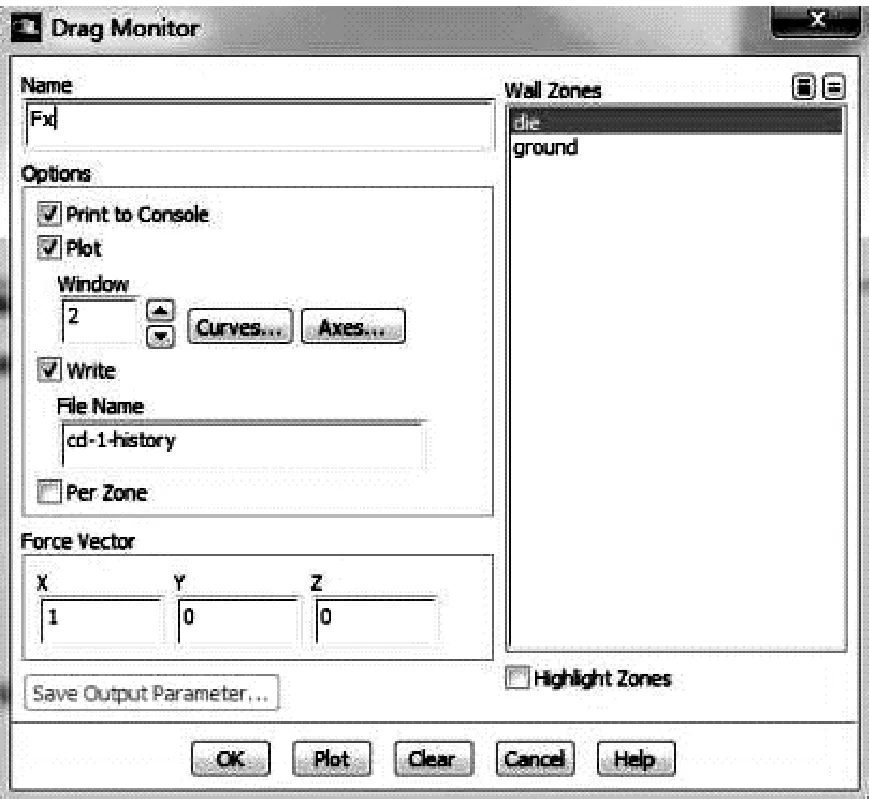
图4 风载荷系数监控设置Fig.4 Setting of monitoring parameters for wind load coefficient

3.2 风载荷系数分析

设计聚光器时，一般要求在8级风速时能正常工作，在8级以上的风速时，保证聚光器不被破坏或损坏。笔者取9级风速的平均值(22 m/s)，5种高度角α分别为0°、30°、45°、60°和90°，7种方位角β分别为0°、30°、60°、90°、120°、135°和180°，聚光器高度角的取值是根据聚光器视日跟踪角度而定的。风载荷方向存在随机性，为便于模拟分析，将风向角转变为聚光器的方位角，故共有35种工况。分别对不同工况进行模拟，得到风载荷系数的变化规律以及在典型工况下的流场特性分布。

聚光器所受阻力来自碟面前、后表面的压力差。不同高度角时阻力系数随方位角的变化如图5(a)所示。聚光器在除90°外的高度角下，以90°方位角为分界，阻力系数的绝对值随方位角的增大呈先减小后增大的趋势。在90°高度角时，聚光器凹面朝上，无论方位角如何变化，其有效迎风面积最小，所以阻力系数最小。在高度角不变、方位角为90°的情况下，聚光器的迎风面积最小，相应的阻力系数也最小。在0°-0°工况下聚光器阻力系数的绝对值最大为1.42。

聚光器所受升力来自碟面上、下表面的压力差。在不同高度角下升力系数随方位角的变化如图5(b)所示。当聚光器高度角为0°和90°时，随方位角的增大，升力系数变化不明显，且高度角α为0°时，升力系数接近0，在其他高度角下各升力系数的变化趋势基本一样。当高度角一定、方位角为0°～90°时，升力系数为负值，说明升力方向朝下，聚光器有向下压的趋势，升力系数的绝对值最大为1.60；当方位角为90°～180°时，升力系数由负值变为正值，升力方向朝上，聚光器有向上浮的趋势，系数的绝对值最大为0.42。

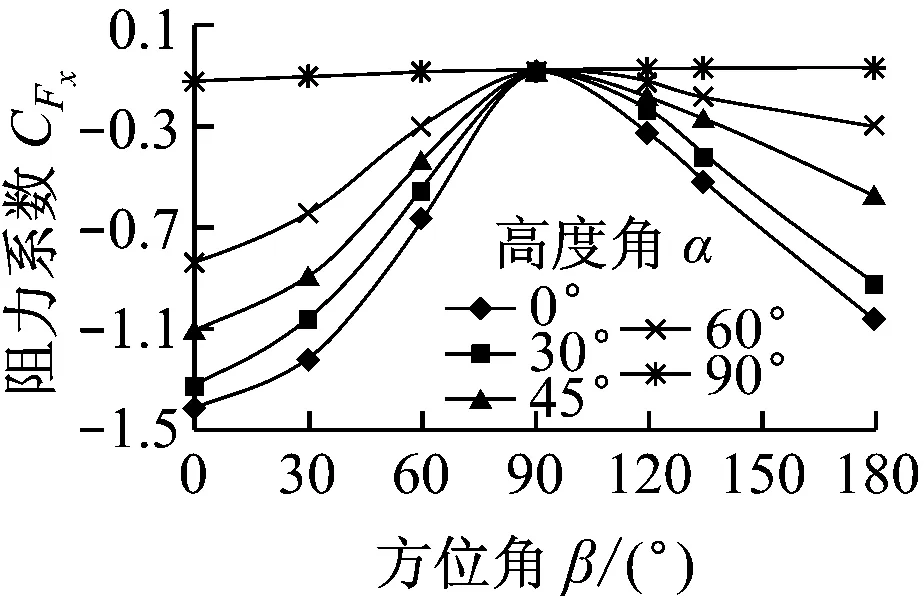
(a) 阻力系数

(b) 升力系数

(c) 侧向力系数图5 不同高度角下各系数随方位角的变化

Fig.5 Changes of various coefficients with azimuth angle at different altitude angles

聚光器所受侧向力来自碟面左、右表面的压力差。在不同高度角下侧向力系数随方位角的变化如图5(c)所示。当方位角一定时，碟式太阳能聚光器的侧向力系数绝对值随高度角的增大逐渐减小。高度角为90°时，侧向力系数基本不随方位角的变化而改变，且数值接近0；高度角α为0°时，侧向力系数的绝对值最大。当方位角为0°和180°时，在各高度角下侧向力系数均近似为0，高度角α为0°时侧向力系数的峰值最大，其值分别为-1.34和0.33，在其他高度角(除90°外)下，侧向力系数随方位角的变化近似呈正弦变化趋势。

翻转力矩是侧向力和升力绕旋转中心作用而产生的力矩。在不同高度角下翻转力矩系数随方位角的变化如图6(a)所示。当聚光器高度角为90°时，无论方位角如何改变，聚光器的凹面均竖直向上，聚光器的边缘部分受风压较大，易导致聚光器绕z轴转动，而聚光器在xoz平面上风压分布均匀，聚光器基本不会绕x轴转动，即翻转力矩系数变化不大，且数值较小。当方位角为0°、90°和180°时各曲线存在最小值，且接近于0，方位角约为60°和135°时出现峰值，其值分别为-0.18和0.02。在各高度角(除90°外)下，翻转力矩系数随方位角的增大近似呈正弦变化趋势，且方位角一定时，翻转力矩系数随高度角的增大而减小。

(a) 翻转力矩系数

(b) 方位力矩系数

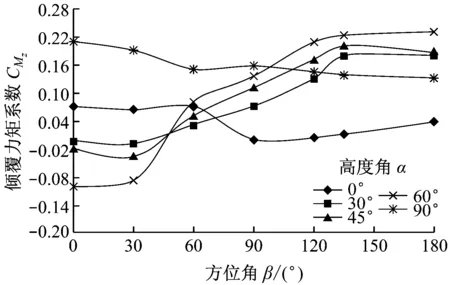
(c) 倾覆力矩系数图6 不同高度角下力矩系数随方位角的变化

Fig.6 Changes of moment coefficient with azimuth angle at different altitude angles

方位力矩是侧向力和阻力绕旋转中心作用而产生的力矩。在不同高度角下方位力矩系数随方位角的变化如图6(b)所示。当聚光器高度角α为90°时，方位力矩系数基本不随方位角的变化而改变，且数值很小；在其他高度角下，各方位力矩系数随方位角的变化近似呈正弦变化趋势；当方位角为30°～60°和120°～135°，在不同高度角下曲线均出现峰值，高度角α为0°时方位力矩系数峰值最大，对应峰值分别为0.15和-0.26。方位角不变，方位力矩系数随高度角的增大而依次减小。

倾覆力矩是升力和阻力绕旋转中心作用而产生的力矩。在不同高度角下倾覆力矩系数随方位角的变化曲线如图6(c)所示。聚光器高度角为90°时，由于其所受升力和阻力变化幅度均很小,在其他高度角(30°、45°、60°)下，倾覆力矩系数绝对值随高度角的增大逐渐增大。在45°方位角附近，倾覆力矩的方向发生改变，倾覆力矩系数为负值时表示聚光器有绕z轴向进风口方向翻转的趋势，倾覆力矩系数为正值时表示聚光器有绕z轴向进风口相反方向翻转的趋势。

以上6种风载荷系数的变化趋势与文献[9]、文献[18]中的实验数据以及文献[11]中的仿真数据基本一致。在整个模拟计算中，部分数值存在一定的误差，后续将进行相应的风洞实验来进一步研究。

3.3 聚光器流场特性分析

聚光器对风有抵挡作用，当风靠近聚光器时，风速减小，风会向聚光器四周扩散分离，导致聚光器边缘部分风速最大，故在其后上方形成空腔，而流过聚光器底部和缺口的气流会上卷，其中部分气流与聚光器背面分离，并形成漩涡现象。由于受篇幅限制，笔者仅对聚光器的最差避风工况(0°-0°)和最佳避风工况(90°-180°)进行对比分析，如图7(a)和图7(b)所示。

图7(a)中聚光器背面有一对很明显的漩涡，其湍流强度最强，而图7(b)中看不到漩涡。当方位角β为0°时，随着高度角的增大，漩涡现象逐渐消失，且聚光器所受最大风压的面积远大于后者，故前者的聚光器更易受损，如图8所示。

当高度角为0°、方位角由0°增大至180°时，聚光器的有效迎风面积先减小后增大，流场湍流强度的变化也呈相同趋势。图9为不同方位角流场速度矢量图。

当方位角为90°时，聚光器有效迎风面积存在最小值，湍流强度较小，对应产生的漩涡较小，为较佳避风工况，如图9(a)所示；当方位角为180°时，聚光器背面迎风，在背风区仍有漩涡现象，但没有0°-0°工况明显，如图9(b)所示。

(a) 0°-0°工况截面(y=0)

(b) 90°-180°工况截面(y=0)图7 不同工况下流场速度矢量图

Fig.7 Velocity vector diagram of the flow field under different working conditions

(a) 0°-0°工况下的正面风压

(b) 90°-180°工况下的背面风压图8 不同工况下聚光器风压分布云图

Fig.8 Wind pressure distribution of the concentrator under different working conditions

4 结 论

(1) 阻力系数与聚光器有效迎风面积成正比，在0°-0°工况下阻力系数的绝对值最大为1.42；随着方位角的增大，升力系数由负值变为正值，其绝对值最大为1.60，聚光器受风载荷作用易出现上浮和下压的现象，故需加强聚光器立柱在地面的固定以及立柱的强度；侧向力系数随方位角的变化近似呈正弦变化规律，当高度角为0°时侧向力系数峰值最大，分别为-1.34和0.33。

(a) 0°-90°工况截面(y=0)

(b) 0°-180°工况截面(y=0)图9 不同方位角流场速度矢量图

Fig.9 Velocity vector diagram of the flow field at different azimuth angles

(2) 在其他高度角(除90°外)下，聚光器翻转力矩系数和方位力矩系数随方位角的增大均近似呈正弦变化规律。当方位角为30°～60°和120°～135°时，方位力矩系数存在峰值，分别为0.15和-0.26，故需加强聚光器立柱的抗扭度；当方位角不变时，翻转力矩系数随高度角的增大而依次减小；当方位角位于60°和135°附近时，翻转力矩系数出现峰值，分别为-0.18和0.02；当高度角不变时，倾覆力矩系数随方位角的增大而增大。

(3) 0°-0°工况为聚光器的最差避风工况，此时聚光器有效迎风面积最大，最大风压分布面积最广，碟面最易受损；90°-180°工况为聚光器最佳避风工况，此时聚光器凹面竖直向上，开口处于背风位置，但迎风面边缘受力最大，故需加强对边缘处镜面的固定，以避免聚光器损坏。