基于模糊自抗扰的风电系统独立变桨距控制
2018-07-25任丽娜刘福才
任丽娜, 刘 素, 刘福才, 张 磊
(1.燕山大学 工业计算机控制工程河北省重点实验室,河北秦皇岛 066004;2.秦皇岛烟草机械有限责任公司,河北秦皇岛 066318)
风能是一种安全、生态和可再生能源,变桨距风力发电机组由于对风能利用的高效性,占据了市场的主导地位[1]。变桨距控制主要有统一变桨和独立变桨2种方式。在统一变桨控制设计过程中,假设风轮旋转平面内风速均匀。但随着风电机组容量的增加和叶片的加长,由风剪切和塔影效应等引起的附加载荷更加严重,俯仰力矩和偏航力矩等也逐渐增大,这不仅影响风电机组运行的稳定性,还会引起输出功率振荡,降低风力机部件的寿命[2]。因此,如何在保证发电质量的同时降低不平衡负荷具有重要的研究意义。独立变桨控制(IPC)[3]是一种旨在稳定发电机的输出功率、降低由不断变化的风力条件造成的风力机负载扰动的控制方法。控制器可根据各叶片不同的受力情况得到不同的叶片桨距角,3个执行器参考不同控制量进行独立操作,因此被称为独立变桨距控制器。近年出现了许多用于降低疲劳负荷、提高发电效率的风力发电机独立变桨距控制策略,包括传统的控制算法,如比例-积分-微分(PID)控制[4]、全状态反馈控制[5]和扰动调节控制(DAC)[6]。现代控制算法的应用进一步提高了风力机的性能。文献[7]中采用基于叶根载荷变换的桨距角反馈线性化独立变桨控制策略,有效降低了动态载荷,但是对于稳定输出功率的效果并不明显。文献[8]中提出了一种最优控制策略,通过对风力机叶片偏移和塔架弯曲进行优化控制,提高了发电机的输出功率,但难以精确地建立实际运行中风电系统的数学模型。文献[9]中提出了一种滑模控制策略,可有效地解决系统中不确定参数的变化,但较易出现抖振问题。
独立变桨距控制一般应用于额定风速以上的恒功率控制,即输出功率是恒定值,因此在额定风速以上的风况下,可将不影响风力机功率输出的风速、风力机的非线性等作为干扰项。自抗扰控制(ADRC)[10]是一种处理干扰的控制算法,是基于误差反馈的非线性控制方法,不依赖于系统精确的数学模型,可对系统的未建模动态和未知扰动作出较好的估计和补偿[11]。鉴于此,为了降低风力机的不平衡负载,保证在额定风速以上的风况下风力发电机的发电质量,笔者将ADRC应用于独立变桨距降载控制中。在实际应用中,针对多个自抗扰控制器不便操作、参数调整困难的缺点,提出了基于模糊逻辑控制(FLC)理论[12]改进的ADRC独立变桨控制,并对闭环系统的稳定性进行了分析。最后通过与传统PD独立变桨、ADRC独立变桨控制策略进行比较,验证了模糊自抗扰控制器(FLC-ADRC)的优越性。
1 风力机描述与建模
1.1 风速模型的建立
1.1.1 风剪切风速模型
图1给出了风速随高度变化的示意图。
随高度变化的风剪切风速模型[13]通常表示为:

图1 风速随高度变化的示意图Fig.1 Variation of wind speed with height
(1)
式中:wshear为由风剪切效应导致的风速变化扰动量;W为轮毂中心高度h处的平均风速;z为风力机叶片高度;m为风剪切系数。
1.1.2 塔影效应风速模型
由于塔架对气流造成堵塞,在塔架上游和下游来流速度均减小,称为塔影效应,可表示为:
(2)
式中:wtower为由塔影效应造成的风速变化扰动量;W0为空间平均风速;a为塔架半径;H为桨叶微元到塔架y轴的轴线距离;L为桨叶微元到塔架x轴的轴线距离。
塔影效应是对作用在叶片上的风速的影响,只产生于下半风轮扫掠面,模型建立较为复杂,因此将塔影效应的风速模型看作未知的外部干扰。
1.2 风力机模型的建立
为了建立有效的风力机独立变桨控制器,笔者采用的独立变桨距控制系统模型如下:
(3)
式中:A为系统的状态矩阵;B为控制输入矩阵;u为控制输入向量矩阵,u=[β1β2β3]T,其中β1、β2和β3分别为3个叶片的输入桨距角;Γ为风速变量输入矩阵;wshear为分别作用在3个叶片上的风剪切风速矩阵,wshear=[wshearwshearwshear]T;wv为分别作用在3个叶片上的塔影效应干扰矩阵,wv=[wv1wv2wv3]T;y为系统模型的状态输出矩阵;x为状态变量矩阵,x=[x1x2x3x4x5x6x7x8]T,其各个状态量含义如表1所示。
根据非线性风力发电机独立变桨距控制系统的动力学方程,其状态空间方程转化形式为[14]:
(4)
式中:Irot为转子转动惯量;Mij、Kij和Cij分别为系统的质量、刚度和阻尼项,其中i,j=1,2,3,5;ζi(i=1,2,3,4)为转子转矩关于桨距角的偏导数;ζbi(i=1,2,3,4)为叶片空气动力关于叶片桨距角的偏导数;r为转子转矩对转速的导数;[w1w2w3]T为包含风剪切的风速输入变量,其中w1、w2和w3分别为3个叶片承受的风速;a为转子转动加速度;ab为每个叶片的一阶偏移速度与作用在叶片上风速的关系。

表1 状态变量Tab.1 State variables
2 独立变桨控制器设计
为了减小叶片疲劳载荷和稳定输出功率,针对3个叶片及转子分别设计FLC-ADRC独立变桨控制器,尽可能减小叶片偏移与功率波动,即使状态变
量的期望值x*=0。将作用于风力机叶片间的耦合、风速和其他不确定因素均归结为未知干扰,通过扩张状态观测器(ESO)对干扰进行实时跟踪估计,并利用非线性误差反馈控制律给予补偿,消除其影响;将模糊逻辑控制应用于自抗扰控制器参数的整定,得到模糊自抗扰独立变桨控制器。为简单起见,笔者以叶片1为例,给出详细的设计步骤,其余状态变量控制器设计类似。
2.1 自抗扰控制器设计
2.1.1 扩张状态观测器设计
以二阶非线性控制对象叶片1为例,设计扩张状态观测器。叶片1的状态空间表达式如下:
(5)
式中:β1为叶片1的控制桨距角。
为设计扩张状态观测器,将叶片1的状态空间表达式转化为:
(6)
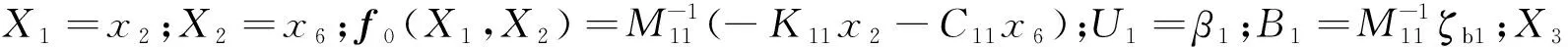

(7)

(8)
式中:Z1、Z2和Z3分别为X1、X2和X3的观测值;β01、β02和β03为相应的观测增益;e1=Z1-X1;B01为B1的大致估计值;e为变量;σ和δ均为给定的参数,其中σ∈(0,1),δ是限制原点附近增益的小数。
为便于表达,用f1(e1)代替fal(e1,σ1,δ),f2(e1)代替fal(e1,σ2,δ)。考虑式(5)和式(6),可得到跟踪误差系统:
(9)

2.1.2 非线性控制律
定义叶片1给定输入与扩张状态观测器观测值之间的误差为:
(10)
式中:r1为叶片1给定偏移量V1与偏移量观测值Z1的误差;r2为叶片2给定偏移速度V2与偏移速度观测值Z2之间的误差。
U1=(KP1+ΔKP1)fal(r1,σ3,δ1)+
(KD1+ΔKD1)fal(r2,σ4,δ2)-(Z3+f0)/B01
(11)
式中:KP1和KD1分别为叶片1自抗扰独立变桨控制器的偏移量和偏移速度增益;ΔKP1和ΔKD1为从模糊逻辑控制器中所得的增益微调。
2.2 自抗扰控制器参数整定
针对风力机参数的不确定性,手动调节各参数大小不利于实际操作。因此,引入模糊控制器,利用模糊规则,在线整定自抗扰控制器参数,以满足不同状态下的参数要求,设计4种不同的FLC应用于风力机变桨控制中,选择用于控制风力机的第1个叶片进行详细阐述。


表2 ΔKP1的模糊控制规则Tab.2 Fuzzy control rule of ΔKP1

表3 ΔKD1的模糊控制规则Tab.3 Fuzzy control rule of ΔKD1
利用上述独立变桨距FLC-ADRC控制器设计方法,针对叶片1提出的控制律如下:
U1=(KP1+ΔKP1)fal(r1,σ3,δ1)+
(12)
图2为风力机模糊自抗扰控制系统框图,其中FLC-ADRC1为上述详细设计结构图,UD为作用在风力机上的风速变量矩阵,UD1为作用在叶片1上风速变量的总和。
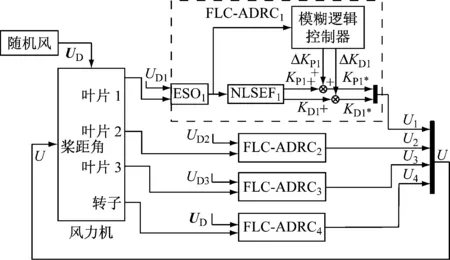
图2 风力机控制系统框图Fig.2 Block diagram of the wind turbine system
2.3 基于模糊自抗扰控制器的系统稳定性分析
定理1:考虑式(6)描述的闭环控制系统,存在式(11)中合适的参数KP1+ΔKP1和KD1+ΔKD1,保证闭环系统稳定,即保证系统的实际输出值X1和X2分别跟踪给定值V1和V2。
证明:对于闭环控制系统,定义给定与系统实际输出之间的误差为:
(13)
式中:s1为叶片1给定偏移量V1与实际输出偏移量X1之间的误差;s2为叶片1给定偏移速度V2与实际输出偏移速度X2之间的误差。
(14)

根据式(10)和式(13),可得到如下形式:
(15)
选择系统(式(15))中的Lyapunov函数[15]:

(s1-e1)(s2-e2)
(16)
(17)
代入式(11)可得:
V3-X3+Z3-B01(KP1+ΔKP1)fal(r1,σ3,δ1)-
B01(KD1+ΔKD1)fal(r2,σ4,δ2)=V3+e3-
B0(KP1+ΔKP1)fal(r1,σ3,δ1)-
B01(KD1+ΔKD1)fal(r2,σ4,δ2)
(18)

(s1-e1)(s2-e2)+β01e1(s1-e1)+(s2-e2)2+
(s1-e1+s2-e2)(V3+β02f1(e1))+
β01e1(s2-e2)
(19)
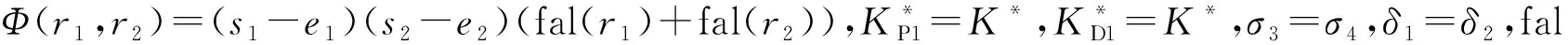
Φ(r1,r2)≥0
(20)
根据文献[16],e1、e2和e3有界,且在实际应用中V3、s1和s2也有界。由于r1=s1-e1,r2=s2-e2,因此r1和r2有界。设:
M=|(s1-e1)(s2-e2)+β01e1s1+(s2-e2)2+
(s1-e1+s2-e2)(v3+β02f1(e1))+
β01e1(s2-e2)|
(21)
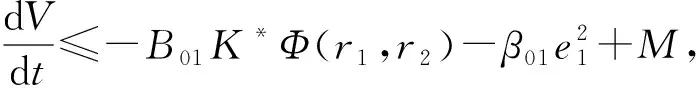
(22)
因此式(13)稳定,X1和X2分别收敛于V1和V2,即输出值与给定值之间的误差趋近0,提出的模糊自抗扰控制器保证了式(6)(闭环系统)的稳定性。
3 仿 真
仿真采用的5 MW风力机参数[18]见表4。采用Matlab仿真验证提出的风力机独立变桨控制器的控制性能。工作区域集中在额定风速以上,其目标是使转子速度和叶片波动最小化。图3给出了风力机轮毂高度处风速在15~20 m/s内的变化。图4给出了作用在3个叶片上的随机风速变化。在FLC-ADRC控制策略作用下3个叶片偏移量见图5。

表4 5 MW风力机参数Tab.4 Parameters of the 5 MW reference wind turbine
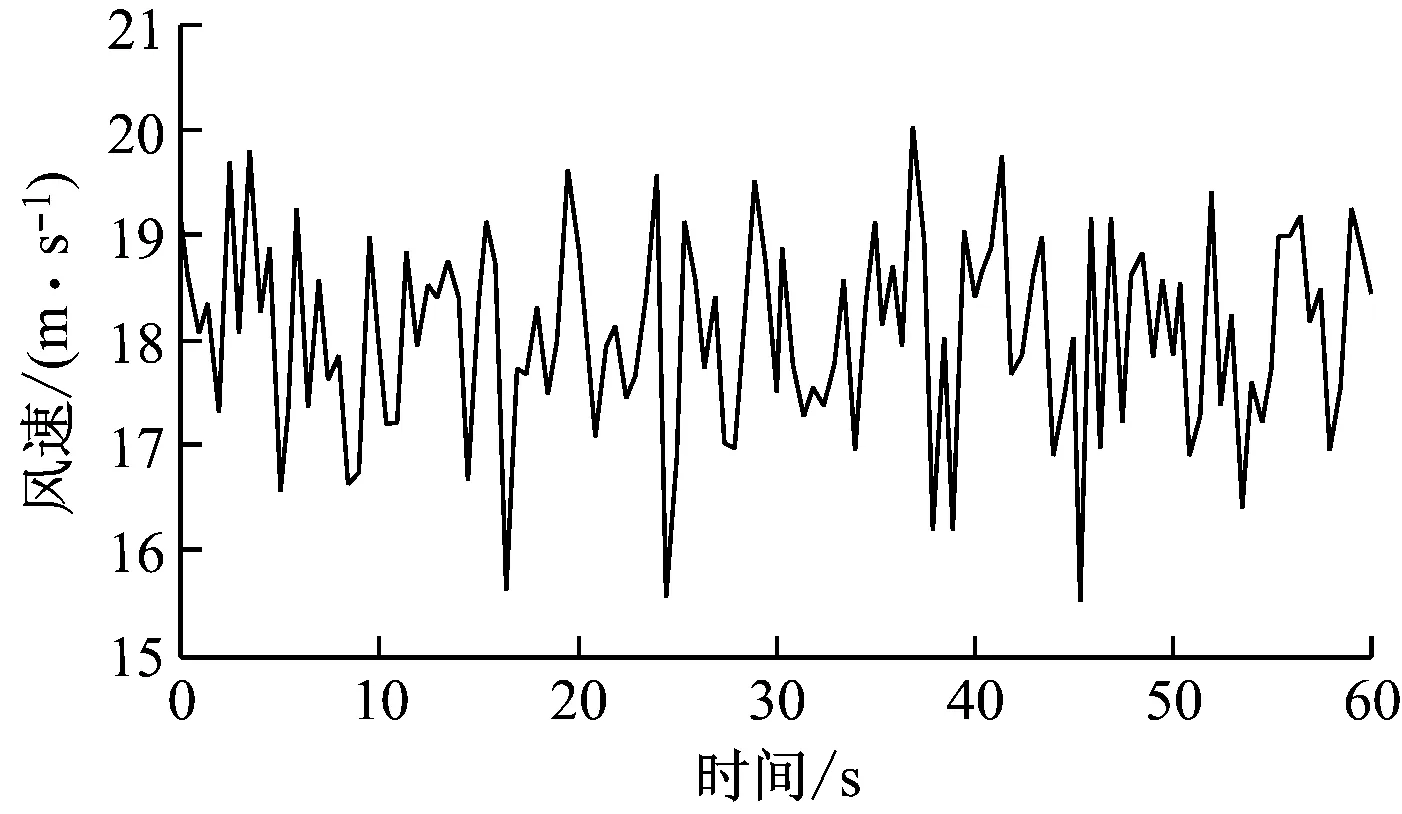
图3 轮毂高度处的风速Fig.3 Hub-height wind speed
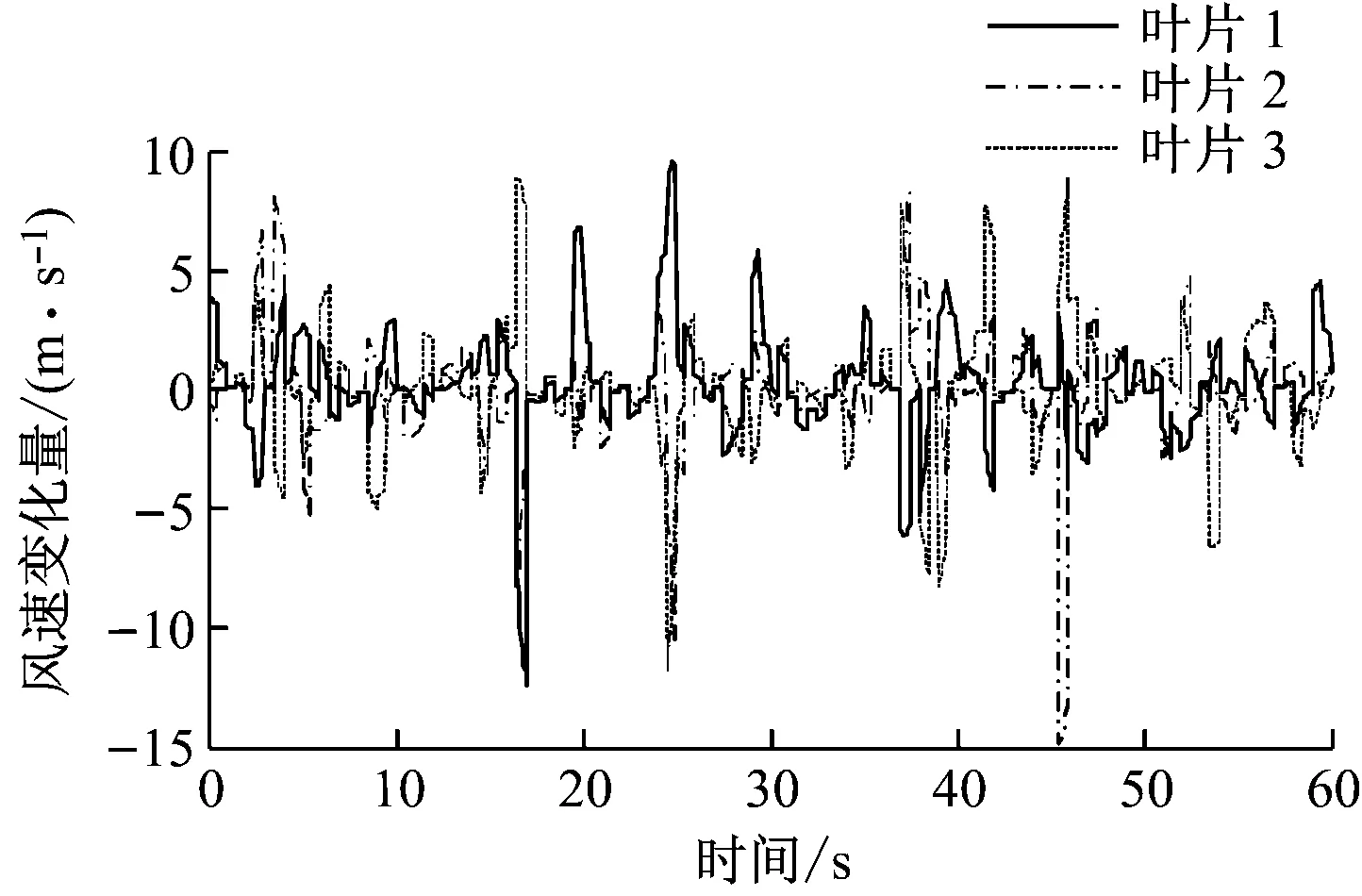
图4 每个叶片的风速Fig.4 Wind speed variation of each blade
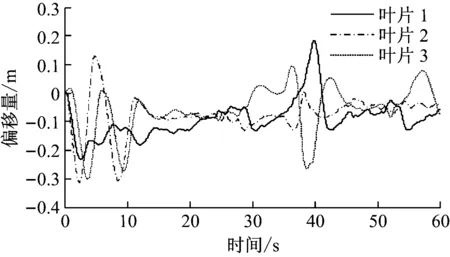
图5 每个叶片的偏移量Fig.5 Offset of each blade
以叶片1为例,图6给出了在FLC-ADRC控制策略下叶片1的叶尖波动和速度变化。由图6可知,根据ESO可很好地估计出叶尖偏移量和偏移速度,偏移速度观测值与输出轨迹几乎一致。图7给出了FLC-ADRC、ADRC和PD这3种不同控制方式下仿真结果的比较。图7(a)和图7(b)分别为不同控制方式下风力机转子的转速和输出功率波动,3种控制方式均能较好地抑制转子的转速波动,保证系统的输出功率较为稳定。由图7(c)和图7(d)可知,叶片尖端偏移量和速度波动的幅度控制在较小范围内,具有较好的动态性能,风力机的疲劳载荷减小,风力机部件的损坏也减少。在应用过程中,FLC-ADRC控制策略更适用于难以建立精确数学模型、运行过程中受随机风速干扰影响严重的风力机系统。
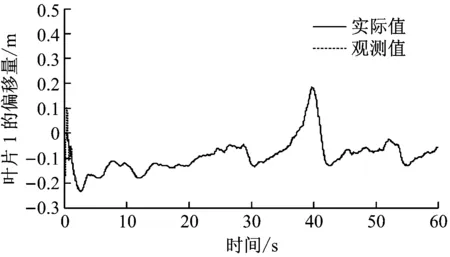
(a) 叶片1的偏移量

(b)叶片1的偏移速度图6 ESO状态跟踪曲线Fig.6 Tracing curve of ESO state
4 结 论
(1)相较于统一变桨,独立变桨能够对各叶片的桨距角分别控制,进而减小模型的非线性和外界不可知干扰造成的不平衡载荷。
(2)应用ESO可对风力机的非线性和随机风速等不可知干扰进行准确估计,应用误差状态反馈控制器使不可知干扰得到有效补偿处理。
(3)应用模糊逻辑理论对参数进行自整定,解决了多个自抗扰控制器存在参数难以调整的问题,简化了调参过程,提高了自抗扰控制器性能。
(4)将提出的控制策略分别与PD控制策略、ADRC控制策略进行Matlab仿真对比,发现在额定风速以上的风况下应用基于模糊逻辑的自抗扰控制器能更有效地保证风力机的发电质量,抑制叶片的偏移,延长风力机的使用寿命。

(a)转子转速波动

(b)功率

(c)叶片1的偏移量

(d)叶片1的偏移速度图7 FLC-ADRC、ADRC和PD仿真结果比较Fig.7 Simulation results of the FLC-ADRC, ADRC and PD
