基于ANSYS Workbench的摇摆装置模态和瞬态分析

□余杨杰 □熊瑞平 □黄文强 □乔治

四川大学制造科学与工程学院 成都 610065

1 问题的提出

核能作为一种重要的能源，主要应用于军事和发电领域。燃料组件是核能装置非常重要的组成部分。燃料组件应用于不同场合时，可能产生不同程度的变形。一旦燃料组件发生较大的变形，则会影响控制棒的插入，导致卡棒，危及核能装置的安全运行[1]。燃料组件应用在舰艇上时，会随着舰艇的晃动而晃动。在晃动过程中，燃料组件可能出现变形。当燃料组件晃动的频率接近自身固有频率时，燃料组件甚至会出现较大的变形，对性能和寿命产生较大的影响。

针对上述问题，笔者结合燃料组件的摆动工况，设计了一种模拟燃料组件在舰艇上的摇摆装置。首先对摇摆装置进行动力学分析，确定了摇摆装置的驱动变力矩。然后对摇摆装置的摆动特性进行分析，研究摇摆装置在摆动过程中的变形量和共振问题。最后对摇摆装置整体进行瞬态分析，保证摇摆装置结构的可靠性[2]。

2 动力学分析

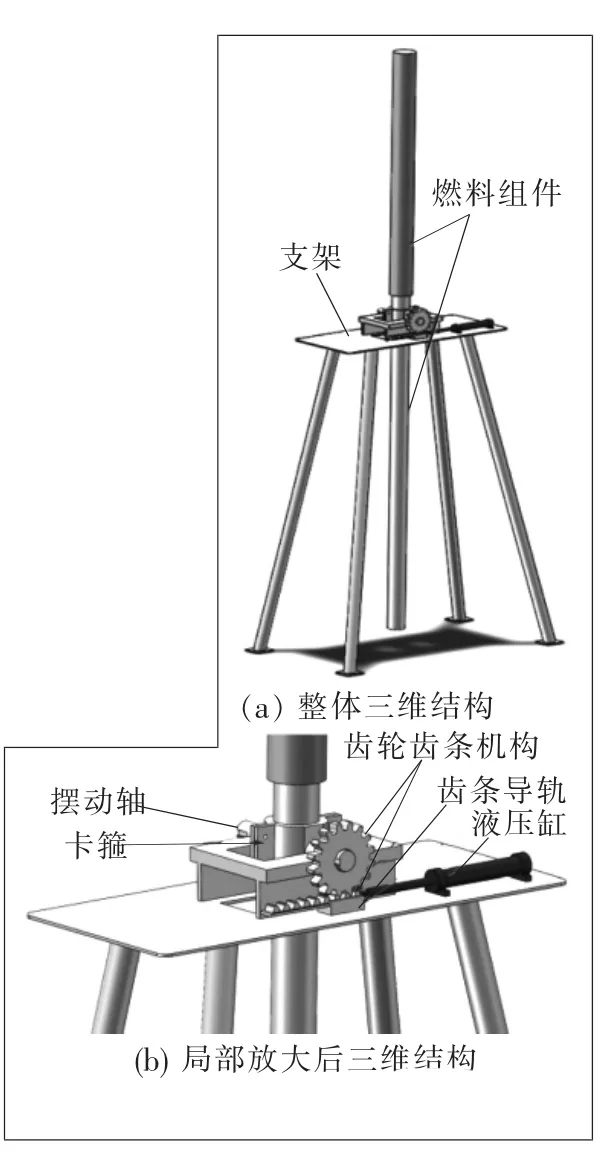
▲图1 摇摆装置三维结构图

图1所示为摇摆装置的三维结构图。图1中上下两段直径不同的圆柱棒为燃料组件，燃料组件下段通过卡箍箍紧，在卡箍端面中心焊接摆动轴，燃料组件、卡箍和摆动轴共同构成摆动件。摆动轴放置在支架上，通过驱动装置驱动摆动轴，使摆动件在支架上来回摆动。驱动装置由齿轮齿条机构、齿条导轨、液压缸等组成，通过液压缸带动齿轮齿条机构中的齿条沿着导轨来回运动，进而带动齿轮转动，最终使与齿轮相连的摆动轴同步转动。根据燃料组件实际摆动情况，确定摆动件的摆动中心，将摆动件的摆动轴安装在燃料组件下段距离过渡端面0.325 m处，摆动轴的直径初定为0.1 m。摇摆装置结构尺寸如图2所示。

已知摇摆装置存在三种比较危险的工况，这三种工况下的摆动角度和时间满足正弦关系。摇摆件的摆角 θ为 3°、7.5°、22.5°，对应的摆动周期 t依次为 12 s、24 s、40 s[3]。

根据摆动件的三维模型，借助计算机软件求得摆动轴到质心的距离为0.822 m。由于摇摆装置的运动为简谐运动，因此其摆长L=0.822 m，摆动周期T′为：

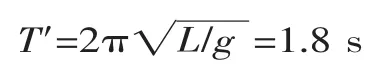
式中：g为重力加速度，g=9.8 m/s2。

可见，摇摆装置自由无阻尼状态下的摆动周期远小于实际工况下的最小摆动周期。为了模拟摇摆装置的真实运动，需要施加一个额外的驱动变力矩，使摇摆装置的摆角和周期满足要求。对摇摆装置摆动件进行受力分析，如图3所示。图3中FN为摆动件所受支撑力，G为摆动件自身重力，Tf为摆动件所受摩擦阻力矩，T为摆动件驱动变力矩。

摆动过程中，摆动轴处的摩擦阻力矩很小，且数值不确定，为简化计算，将其忽略，则摆动件驱动变力矩为：

式中：m为摆动件质量；J为摆动件转动惯量；α为摆动件角加速度。

三种工况下的角位移函数分别为：

▲图2 摇摆装置结构尺寸

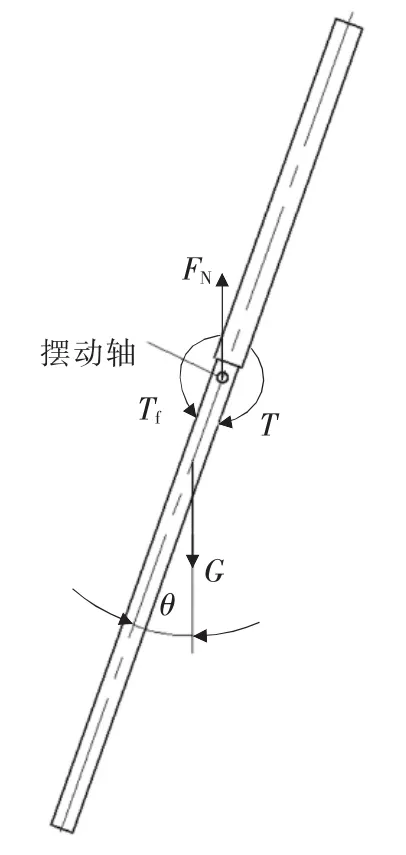
▲图3 摆动件受力分析

对角位移函数求二阶导数，可得角加速度函数[4]：

通过软件求得摆动件的转动惯量J=11 991 kg·m2，联立式（2）～式（7），可求得三种工况下摆动件所需施加的驱动变力矩：

3 有限元建模

应用ANSYS Workbench软件对摇摆装置进行模态和瞬态分析，需要建立摇摆装置的三维模型。应用SolidWorks软件建立摇摆装置的三维模型，通过SolidWorks与ANSYS Workbench的接口，将模型导入ANSYS Workbench，进行摇摆装置的有限元分析。

由于驱动装置只对摆动轴提供一个驱动力矩，且其质量较小，因此为了减少计算量和求解时间，将驱动装置用一个外力代替，其提供的驱动变力矩直接施加在摆动轴上[5]。

3.1 材料特性

由于燃料组件的实际材料构成非常复杂，因此笔者对其材料构成进行简化替代，上段材料采用铝合金，下段材料采用结构钢。摇摆装置的其它结构，包括卡箍、摆动轴及支架同样采用结构钢材料。摆动过程中受力部位主要集中在卡箍及支架上，所以在对燃料组件进行有限元分析时，主要考虑结构钢的材料特性能否满足要求。结构钢为45号钢，其弹性模量为200 GPa，泊松比为 0.3，密度为 7 800 kg/m3[6]。

3.2 网格划分

网格划分是建立有限元模型的重要环节，网格划分的质量对模型有限元分析结果的准确度和速度有重要影响。对摇摆装置进行自由网格划分，燃料组件单元类型为Solid187，卡箍、摆动轴及支架单元类型为Solid186。此外，摆动轴、螺栓连接处及支架凸台根部结构强度可能较弱，在自由网格划分的基础上对这几处网格进行局部加密细化。划分网格后，摇摆装置的网格数为 109 314，节点数为 215 362[7]，有限元模型如图 4所示。

▲图4 摇摆装置有限元模型

▲图5 摇摆装置振型

4 模态分析

在摇摆装置有限元模型建立完成后，对其进行模态分析，得到摇摆装置的振动特性，包括固有频率和振型，判断摇摆装置在摆动过程中是否会发生共振，同时也为瞬态动力学分析奠定基础。

在分析时，支架处于固定状态，对支架底部的四个面施加固定约束。对摆动轴施加圆柱面约束，使其径向和轴向固定，圆周方向处于自由状态。对于卡箍连接的螺栓处，用仅有压缩面的约束代替螺栓作用。在约束添加完成后，还需对摇摆装置施加预应力，包括卡箍处及驱动装置处的预应力。

提取前十二阶固有频率，对应的最大变形和振型见表1。部分阶数振型如图5所示[8]。

对摇摆装置各阶固有频率和振型进行分析。

摇摆装置的前四阶振型变形主要位于燃料组件上，且最大变形都位于端部。摇摆装置的五至十二阶振型变形主要集中在支架上，最大变形位于支架立柱中间位置处。

摇摆装置的振型与其对应的固有频率呈高度关联，各阶的固有频率越接近，对应的振型也越相似。

摇摆装置振型的最大变形理论上应随固有频率的增大而增大，但表1数据并非如此，分析其原因，一是最大变形可能出现在两根立柱上，则该振型的最大变形量可能小于低阶固有频率对应振型的最大变形量；二是出现最大变形位置的面积较大，则该高阶振型对应的最大变形量可能小于低阶频率对应振型的最大变形量。

摇摆装置三种工况下的摆动周期分别为12 s、24 s、40 s，则最大摆动频率为1/12 Hz，远小于一阶固有频率6.87 Hz，因此，摇摆装置在摆动过程中不会发生共振[9-10]。

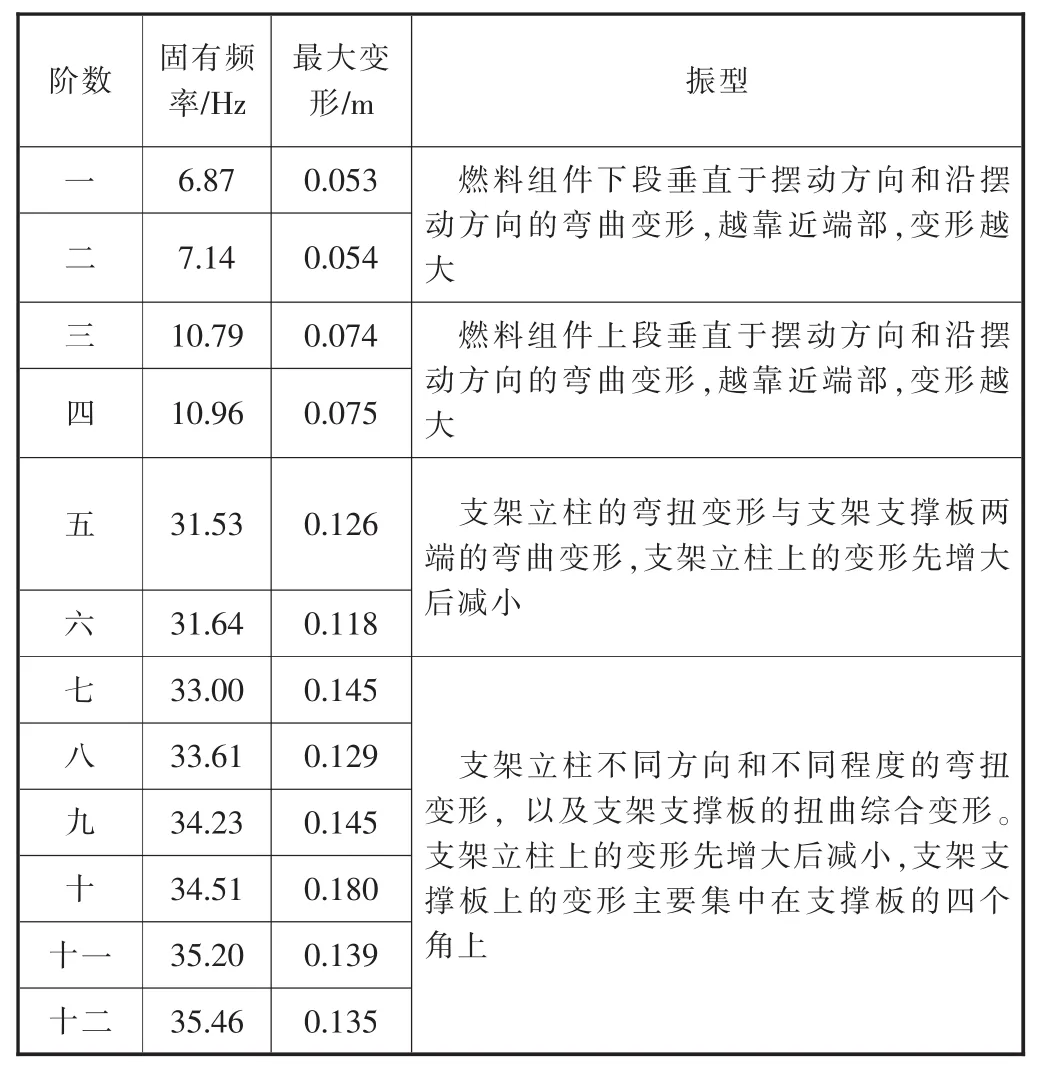
表1 前十二阶固有频率值

5 瞬态分析

虽然对摇摆装置进行模态分析得出不会发生共振的结论，但仍需进一步对摇摆装置进行瞬态分析，确保摇摆装置整体结构设计的可靠性。在瞬态分析过程中，对摇摆装置添加的约束与模态分析相同。在约束添加完成后，还需在ANSYS Workbench中施加重力。重力方向为-Y轴，同时对摆动件施加旋转加速度。驱动装置用一个外力代替，作用在支架支撑板上，然后在摆动轴上施加驱动变力矩。

在动力学分析过程中已求得三种驱动变力矩，则可以确定对应的函数曲线，如图6所示。

▲图6 驱动变力矩函数曲线

由图6可知，驱动变力矩T3的幅值最大，对摇摆装置结构强度的影响也最大。笔者在驱动变力矩T3作用下进行瞬态分析，计算求解摇摆装置的应力和最大变形。

对摇摆装置进行瞬态分析后，提取其在驱动变力矩T3作用下的最大应力图和总变形图，分别如图7、图8所示。由图7可见，最大应力为41.5 MPa；由图8可知，最大总变形为811 μm。

摇摆装置的最大应力位于卡箍螺栓连接处，最大总变形位于支架立柱中间位置处，两者出现在不同的位置，原因应该与摇摆装置不同位置的受力、结构尺寸差异及结构外形设计有关。

在对摇摆装置施加驱动变力矩T3时，最大等效应力为 41.5 MPa，小于材料的许用拉应力（250 MPa）；最大总变形量为811 μm，相对于摇摆装置整体尺寸而言很小，满足结构安全要求。

6 结论

针对燃料组件在舰艇上的摆动问题，笔者设计了一种用于模拟的摇摆装置。对摇摆装置进行动力学分析，得出所需施加在摇摆装置上的驱动变力矩，并在此基础上应用ANSYS Workbench软件对摇摆装置进行模态和瞬态分析。结果表明，摇摆装置在摆动过程中不会发生共振，且其结构设计安全可靠，满足强度要求。笔者研究对燃料组件在舰艇上的应用有一定参考价值。

▲图7 摇摆装置最大应力图

▲图8 摇摆装置总变形图