复杂结构件疲劳可靠性模型与评估技术研究

胡杰鑫, 谢里阳, 尹伟, 白恩军, 吕骁

(1.东北大学航空动力装备振动及控制教育部重点实验室, 110819, 沈阳; 2.北京强度环境研究所, 100076, 北京; 3.上海微创医疗器械(集团)有限公司, 200120, 上海)

经典的应力-强度干涉模型虽然已经普遍地应用于零部件(或是只包含单疲劳细节的结构部件)的疲劳可靠性评估[1-4],但却存在一些问题,例如:疲劳载荷难以统计,指定寿命下的疲劳强度概率密度分布难以确定,只能评估载荷一次作用下的静强度可靠性。为了获得某一寿命所对应的疲劳强度分布,许多学者提出了利用指定应力水平下的寿命分布来推导指定寿命条件下疲劳强度分布的方法[5-6],然而这些研究结果均是在恒幅循环载荷条件下获得的,对于变幅载荷情况下的疲劳可靠度预测问题则具有一定的局限性。另外,也有一些学者试图从材料在不同载荷作用下的损伤演化规律中得到静强度退化方程[7-10],进而得到零件在不同寿命下的剩余静强度,但剩余静强度的分散性却往往被假设成线性的。

近年来,谢里阳、王正从统计平均角度重新解释了应力-强度干涉模型,打破了传统可靠性模型中2个变量必须是同量纲的限制,提出了能够直接应用应力分布和寿命分布进行疲劳可靠度计算的异量纲干涉模型[11],相较于推导疲劳强度分布所面临的数学困难,疲劳寿命分布更容易从试验中获得,因此这种方法大大降低了疲劳可靠性分析的难度,简化了分析步骤。

对于多部位损伤结构的失效问题,国内外学者已进行了广泛的研究。机身铆钉搭接结构的多铆钉孔是典型的多部位损伤结构,目前的研究也主要是针对这种结构。许多研究表明:多铆钉孔的损伤能够使机身结构的强度降低20%～40%,甚至可以达到60%,且应力强度因子呈现出快速增长趋势[12-14]。Shi等研究了铆钉搭接结构在腐蚀环境下的多部位损伤疲劳可靠性问题,在认为一个疲劳细节失效就会导致结构系统失效的前提下,应用一次二阶矩法计算了结构可靠度[15]。王卫国等基于多疲劳细节之间失效相互独立的假设,研究了压气机轮盘可靠度的计算方法[16]。值得注意的是,以上研究均未考虑各疲劳细节之间的失效相关问题。实际上,含有多个疲劳细节的结构件可以看作是由多个只含有单一疲劳细节的单元构成的系统,因此,复杂结构件的可靠性问题可以转化为系统可靠性问题。失效相关性普遍存在于机械系统中,相关程度取决于载荷不确定性和各单元强度不确定性的相对大小,其中载荷不确定性是导致失效相关的根本原因[17]。

目前,对于失效相关问题的研究国内学者已取得了一些成果,例如:钱文学在没有假设各薄弱部位失效相互独立的前提下,直接从系统层建立了随机恒幅载荷作用下含有多个相同结构尺寸的薄弱部位结构的可靠性模型,并分析了安全裕量和载荷粗糙度对可靠度的影响,认为高的安全裕量可以提高多薄弱部位结构的可靠度,且在安全裕量一定时,高的载荷粗糙度可以降低多薄弱部位结构可靠度对薄弱部位数目的敏感性[18-19];Xie等研究了多个压气机叶片组成的串联系统的可靠性问题,并分析了失效独立与失效相关之间的差异,认为假设各零部件之间失效独立会低估串联系统的可靠度,得到较为保守的结果[20]。

综上所述,对于含有多个疲劳细节的结构的可靠性研究还仅局限于一些简单的情况:载荷简单,均为确定性载荷或随机恒幅载荷;结构简单,如含有多铆钉孔的机身结构、航空发动机轮盘结构等;各疲劳细节的材料性能独立同分布,几何尺寸也都相似,在同一载荷作用下各疲劳细节的应力都一样。然而,对于列车枕梁这类复杂结构,以上的所有情况都不满足,因为列车在运行过程中承受随机变幅载荷;枕梁上的疲劳细节涵盖了母材和焊缝,不同疲劳细节的材料性能分布也不相同;各疲劳细节的几何尺寸不一样,即使在同一载荷作用下各疲劳细节的应力也有显著差异。如何处理好这些问题,将成为对枕梁这类复杂结构部件进行可靠性分析的关键。

本文基于疲劳可靠度异量纲干涉模型,结合系统可靠性理论,在不做失效相互独立假设的前提下建立了含有多个疲劳细节结构的可靠性模型,并将理论模型与蒙特卡罗仿真相结合,提出了一种评估随机变幅载荷作用下复杂结构可靠性评估的新方法,并以列车枕梁为研究对象,对其进行了疲劳可靠性评估。

1 应力-寿命干涉分析及系统疲劳可靠性模型

在应力-强度干涉模型中,应力和强度这2个随机变量同量纲,应用这个模型来计算疲劳可靠度需要已知指定寿命下的疲劳强度分布,但由于数学推导困难,准确的疲劳强度分布很难得到。

谢里阳、王正通过对应力-强度干涉模型进行统计平均解释,得到了可以直接利用疲劳试验所获得的寿命分布来计算疲劳可靠度的应力-寿命干涉模型,表达式[11]为

(1)

式中:N是具体寿命;n是寿命变量;f(s)是应力概率密度函数;s是标识应力;g(n|s)是在应力历程s下的寿命概率密度函数。

式(1)只适用于含有1个疲劳细节(或者1个零件)的可靠度计算。由多个疲劳细节构成的复杂结构件可以看作是由多个单元组成的系统,因此复杂结构件的可靠性可以采用系统可靠性方法进行处理。但是,由于各疲劳细节在不确定载荷作用下存在着失效相关性[17],故不能用假设各部位失效相互独立的传统可靠性模型来计算系统可靠度。

假设指定的应力历程为s,则单个疲劳细节的可靠度可以表示为

(2)

假设系统是由多个疲劳细节组成的k/m系统(表决型系统,m为系统中的单元总数),即系统中有m-k个以上单元失效时系统才失效,同时假设各疲劳细节的寿命独立同分布。根据系统可靠性理论,在确定载荷的作用下,各疲劳细节的失效相互独立[20],则在指定的应力历程s的作用下,系统的条件可靠度可以表示为

(3)

当k=m时,得到串联系统可靠性模型

(4)

此模型适用于不允许任何疲劳细节失效的系统。

当k=1时,得到并联系统可靠性模型

(5)

此模型适用于不允许全部疲劳细节都失效的系统。

在随机载荷作用下,各类系统可靠度的表达式分别为

(6)

(7)

(8)

当各疲劳细节的寿命分布不同时,假设在指定的应力历程s下,各疲劳细节的寿命概率密度函数分别为g1(n|s),g2(n|s),…,gm(n|s),则系统的可靠度(以串联系统为例)可以表示为

(9)

若各疲劳细节所受的应力也不相同,设第i个疲劳细节的应力服从正态分布,即si～N(μi,σi2),可以通过式(10)获得其与标准正态分布s0～N(0,1)之间的关系

(10)

将式(10)代入式(9),得到串联系统的可靠度为

(11)

若采用传统的串联系统可靠性模型,即各个疲劳细节的失效相互独立,则串联系统可靠度的表达式为

(12)

对比式(11)和式(12)可以发现,虽然只是简单地改变了计算顺序,但式(11)是从系统层级上直接应用应力-寿命干涉模型建立的,它不仅考虑了由于载荷的不确定性而导致的疲劳细节失效的统计相关性,而且避免了由于假设疲劳细节失效独立而导致低估串联系统可靠度的问题[20]。

2 随机载荷历程下复杂结构件的疲劳可靠度计算方法

复杂结构件在实际使用中往往承受随机变幅载荷作用,因此有必要讨论在这种载荷环境下复杂结构件疲劳可靠度的计算方法与步骤。

首先考虑复杂结构件中单个疲劳细节在随机变幅载荷历程下的疲劳可靠性问题,然后再推广到多个疲劳细节构成的系统疲劳可靠性问题。单个疲劳细节的疲劳可靠度计算步骤如下:

(1)选取一个确定的载荷历程,通过力学计算转化为疲劳细节的应力历程;

(2)利用雨流计数法获得疲劳细节应力历程中各循环的应力均值与幅值以及循环次数;

(3)利用平均应力修正公式,将疲劳细节应力循环中的非对称循环转化为对称循环(对于估算疲劳寿命问题,应用Goodman平均应力修正公式得到的结果较保守);

(4)采用蒙特卡罗方法[21],从材料的p(存活率)-s-N曲线簇中抽取l条s-N曲线(根据超高周疲劳研究的结论,材料在低于传统疲劳极限的循环应力下运行多于1 000万次以上时仍会发生疲劳,因此,本文假设疲劳细节的材料不存在传统意义上的疲劳极限,这样的计算结果较为保守且能满足使用安全的要求),结合步骤(3)获得的疲劳细节应力历程,对每条s-N曲线应用累计损伤法则(本文采用Miner线性累计损伤法则[22])获得疲劳细节的寿命值,最后得到l个寿命样本;

(5)根据材料的中值s-N曲线,应用Miner线性累计损伤法则将步骤(3)获得的疲劳细节应力历程转化为恒幅循环应力,并将此恒幅循环应力的幅值作为该载荷历程的标识应力,这样获得的标识应力可以避免评估结果出现保守或危险的情况;

(6)通过拟合步骤(4)获得的l个寿命样本,得到在步骤(5)获得的标识应力下的寿命分布;

(7)多次重复步骤(1)～(6),得到不同载荷历程下的标识应力和相应的寿命分布;

(8)寻找寿命分布参数与标识应力之间的关系,将各寿命分布参数用标识应力表达,得到只包含应力参数的寿命分布函数;

(9)拟合不同载荷历程下的标识应力,得到标识应力分布函数;

(10)通过式(1)计算出任意指定寿命下单个疲劳细节的疲劳可靠度。

对于多个疲劳细节构成的系统,模仿步骤(1)～(9)得到各个疲劳细节的寿命分布函数与应力分布函数,然后应用式(11)计算出多个疲劳细节构成的串联系统疲劳可靠度。

3 枕梁的疲劳可靠度计算

枕梁(长2.4 m,宽3.35 m,高0.44 m)是一个几何形状复杂且包含多个疲劳细节的复杂结构件,主要承受空气弹簧载荷、抗蛇行载荷和中心销载荷,如图1所示。

图1 列车枕梁承载示意图

根据有限元计算结果,在枕梁左侧选取3个疲劳细节(如图2所示,疲劳细节1和疲劳细节2位于角接焊缝上,疲劳细节3位于母材上)。由于枕梁结构及其所受载荷均左右对称,在枕梁右侧也存在3个疲劳细节与左侧的疲劳细节相对应,且两边对应位置的应力历程和寿命分布相同,因此共需考虑枕梁上的6个疲劳细节。

图2 列车枕梁左侧疲劳细节

将列车枕梁看作是由这6个疲劳细节组成的串联系统,采用本文方法计算列车枕梁的疲劳可靠度。

3.1 疲劳细节的标识应力及寿命分布

根据欧盟标准EN12663—1[23],假设在某一线路上行驶的列车的枕梁所承受的空气弹簧载荷恒定,抗蛇行载荷和中心销载荷每10 min循环一次直至破坏,即载荷历程循环周期为600 s,具体的载荷历程如图3所示。

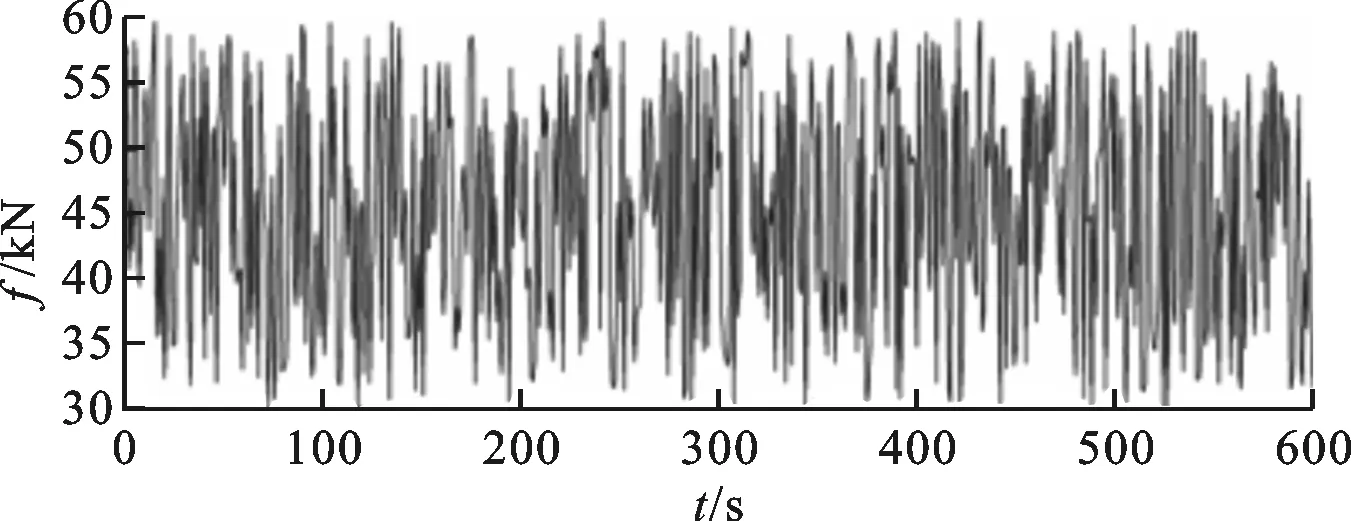
(a)中心销载荷

(b)抗蛇行载荷图3 列车枕梁载荷历程

按照前述步骤(1)～(4),计算各个疲劳细节的寿命样本值。以疲劳细节1为例,该疲劳细节的应力历程经雨流计数法处理后的结果如图4所示,图5为Goodman平均应力修正前后的示意图。

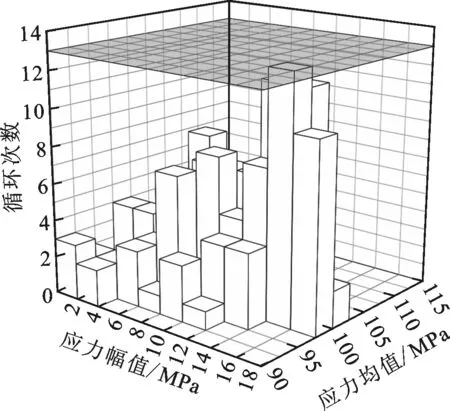
图4 应力循环统计结果

图5 平均应力修正效果示意图

疲劳细节1使用的p-s-N曲线[24]如图6所示,10 000个仿真数据的统计结果如图7所示。

图6 角接焊缝的p-s-N曲线

图7 疲劳细节1的寿命仿真数据统计图

按照前述步骤(5),计算图3所示载荷历程的标识应力,图8为其应力等效示意图。

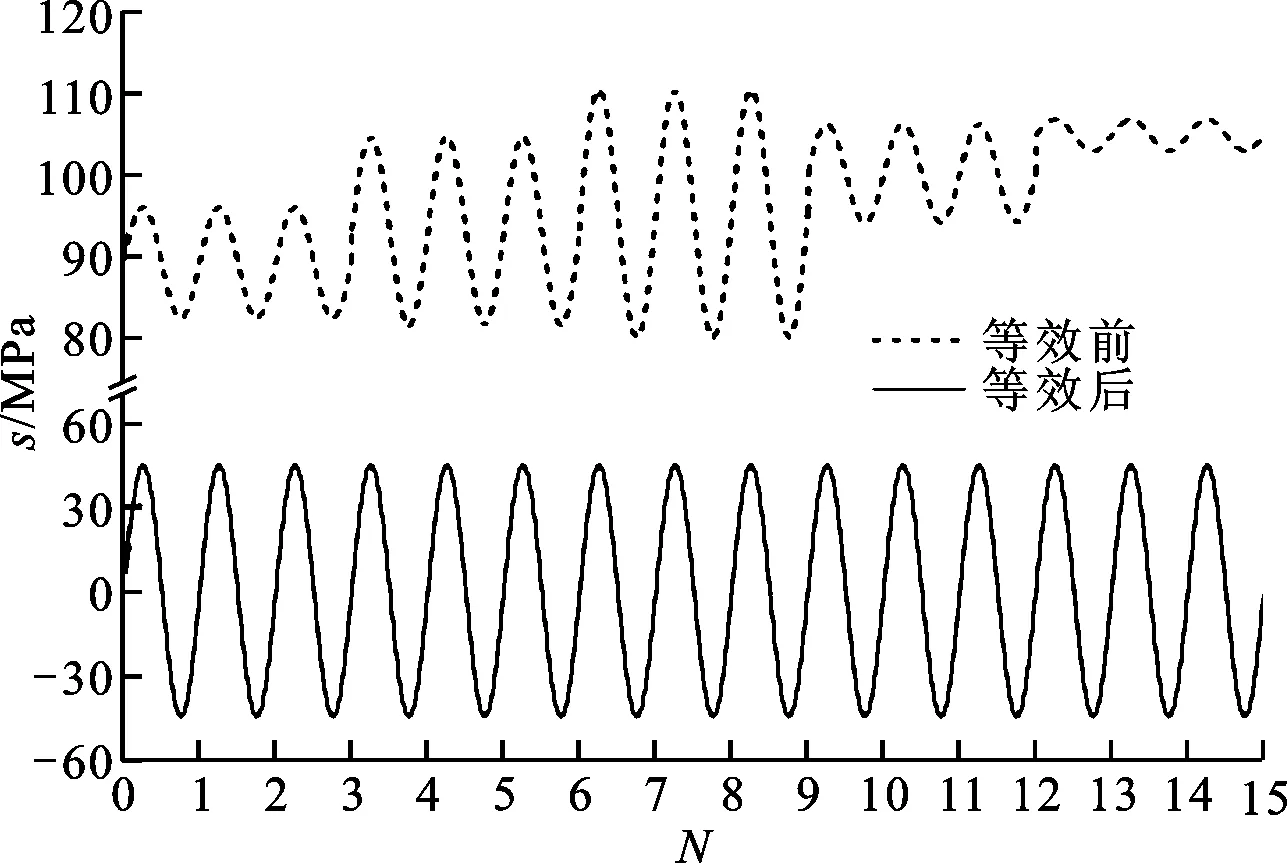
图8 应力等效示意图

在图3所示的载荷历程下,求得的3个疲劳细节的标识应力(步骤(5))及其寿命威布尔分布参数(步骤(6))见表1。

表1 标识应力与寿命威布尔分布参数

3.2 疲劳细节的寿命分布函数

对于同种材料,一般情况下寿命威布尔分布的尺度参数η直接与应力有关,而形状参数β可以认为与应力无关,并且大量试验结果也表明:疲劳寿命威布尔分布的形状参数主要取决于材料、结构及失效机理,对应力不敏感[22]。表1中各疲劳细节的寿命分布参数恰好验证了这一结论。

通常尺度参数与应力的关系可以表示为

η(s)=10a+blgs

(13)

式中a、b为待定系数。

根据EN12663—1标准[23]选用合理的载荷参数,设计不同的载荷历程。按照3.1小节中的分析过程,分别计算各个载荷历程下3个疲劳细节的标识应力与寿命分布参数(步骤(7))。利用最小二乘法[25]拟合式(13)中的待定系数a、b,由于形状参数对应力不敏感,故将各个载荷历程下的形状参数简单地取算术平均值(步骤(8)),拟合结果见表2。

表2 寿命分布函数的拟合参数

以疲劳细节1为例,在指定标识应力s下,其寿命概率密度函数可以表示为

(14)

3.3 含多个疲劳细节结构的疲劳可靠度

对于在不同线路上行驶的列车,枕梁所承受的载荷历程也不相同。经过统计计算得到的不同线路上枕梁各个疲劳细节的标识应力均服从正态分布(步骤(9)),具体的分布参数见表3,与图2所示枕梁左侧疲劳细节相对应的右侧3个疲劳细节的应力分布与这3个疲劳细节的应力分布分别相同。

表3 标识应力分布参数

通过式(11)和式(12)分别计算列车枕梁的可靠度与寿命之间的关系,所得结果如图9所示。

图9 枕梁可靠度随寿命的变化曲线

图9中,虚线是根据传统的串联系统可靠性模型(式(12))计算得到的,即假设各个疲劳细节的失效相互独立;实线则是根据本文提出的串联系统可靠性模型(式(11))计算得到的,即考虑了各个疲劳细节失效的统计相关性。从图9中可以看出:传统的系统可靠性模型计算的可靠度偏于保守;该列车枕梁服役30年后的可靠度约为0.90。由于本文所使用的列车枕梁载荷历程是根据EN12663—1标准设计的,比实际服役的载荷历程要严酷,因此,所计算的列车枕梁服役30年后的可靠度较实际情况要保守。

4 结 论

(1)将含有多个疲劳细节的复杂结构件看作由多个只含有单一疲劳细节的单元构成的串联系统,基于应力-寿命异量纲干涉分析原理,提出了一种复杂结构件疲劳可靠性模型。与前人所研究的模型相比,该模型适用于复杂载荷情况(如随机变幅载荷)、复杂结构情况(如各个疲劳细节的几何尺寸均不相同,即在同一载荷作用下各疲劳细节的应力有显著差异)以及各个疲劳细节的材料性能完全不同的情况(如疲劳细节出现在母材或焊缝上)。

(2)与多个零件组成的机械系统一样,在载荷不确定的情况下,有多个疲劳细节的结构内也存在着失效相关性,本文提出的系统疲劳可靠性模型能体现各个疲劳细节之间的失效相关性。

(3)列车枕梁各个疲劳细节寿命的威布尔分布参数表明,对于同种材料,尺度参数与应力有关,而形状参数对应力不敏感,这与前人研究的结果一致。