融合低秩和稀疏表示的图像超分辨率重建算法
2018-07-25宋长明王赟
宋长明, 王赟
(中原工学院理学院, 451191, 郑州)
图像分辨率可以理解为图像的可分辨能力,通过升级成像设备的硬件可以得到更高分辨能力的图像。但是,设备升级技术突破困难,生产代价高,并且升级后设备的成像仍然易受环境影响,因此常采用超分辨率(super-resolution,SR)重建算法来提升图像的分辨能力。从1幅或多幅退化的低分辨率(low-resolution,LR)图像得到高分辨率(high-resolution,HR)图像的图像处理算法,称为图像超分辨率重建算法。
当前,图像超分辨率重建主要利用基于插值、重建和学习的3类算法。基于插值的算法任务量小,直观且易于实施,其中双三次插值利用采样点4×4邻域内16个已知像素点的灰度值来估计采样点的灰度值[1];用Lanczos插值算法计算像素值的权重信息,重建效果良好[2]。但是,基于插值的算法没有充分利用图像的高频信息,重建的图像会出现边缘、纹理缺失,存在明显的块效应。基于重建的算法加入了图像的先验信息来指导建模重建,代表性的方法有迭代反投影法(IBP)、最大后验概率法(MAP)和凸集投影法(POCS)等[3],其中最大后验概率算法利用统计模型描述图像的纹理分布,提升了重建的效率,具有较好的稳定性,但却依赖于图像的先验信息,重建图像的纹理过于平滑,收敛速度慢,难以用于实时操作。基于学习的算法利用学习到的高、低分辨率图像间的特征映射关系建模重建,最早由Freeman提出,通过在马尔科夫随机场内建模,可以重建出更多的高频细节,但是计算负担大,效率低[4-5]。2004年,Chang等结合流形的相关理论,提出了基于邻域嵌入的超分辨率算法,克服了对样本的依赖[6]。2008年,Yang等以低分辨图像作为先验约束,充分利用了图像间的结构和内容信息,提出了基于稀疏编码的图像超分辨率重建(ScSR)算法,重建效果更好,被广泛推广与应用[7]。近年来,许多学者对基于学习的重建算法进行了大量研究,例如:侯兴松等在方向提升小波变换域进行稀疏滤波,有效消除了压缩感知中的混叠干扰[8];郝雯洁等采用了子半阈值迭代算法,使稀疏重建性能更加鲁棒[9];Dong等对图像进行了非负稀疏编码,符合实际应用的要求[10];Huang等提出了非局部低秩正则化重建模型,充分利用了图像的非局部自相似性[11]。
本文主要研究含有噪声图像的超分辨率重建,为了避免直接重建的不稳定性,采用多层串联方案[12]来逐层提升图像的质量。针对图像SR重建算法效率低、易受退化噪声影响的问题,结合低秩矩阵恢复与稀疏重建理论对退化图像首先进行低秩恢复,得到低秩和稀疏部分,然后对低秩部分利用稀疏重建理论重建。对退化图像低秩恢复后再重建,一是排除了图像噪声对于重建过程的影响,二是提升了算法的效率。实验结果表明,本文算法在运行速度和峰值信噪比方面均效果良好。
1 基于稀疏表示的超分辨率重建理论
图像的超分辨率重建与其退化过程相逆。将图像的退化模型化:假设X为高分辨率图像,则对应的低分辨率图像可表示为
Y=SHX
(1)
式中:S是降采样矩阵;H是模糊矩阵[13]。
对于高分辨率图像块x,在由高分辨率图像样本训练得到的过完备字典Dh下有最稀疏表示α,则对于低分辨率图像块y,有
y=SHx=SHDhα=Dlα
(2)
式中Dl=SHDh为低分辨率字典。式(2)说明,高、低分辨率图像块在对应的过完备字典下稀疏表示相同。因此,在重建阶段,对于退化图像块y,求解下述优化问题
min‖α‖0, s.t.‖y-Dlα‖0≤δ
式中δ为预先设定的稀疏表示误差。得到上述优化问题的解α后,利用Dh就能重建出高分辨率图像块。采用拉格朗日乘子法求解,即
(3)
上述重建理论成立的基础是高、低分辨率图像块在对应过完备字典对下的稀疏表示相同,因此要求Dh与Dl尺寸相同[7]。
2 融合低秩和稀疏表示的超分辨率重建理论
2.1 图像低秩恢复理论
低秩矩阵恢复是继数据的稀疏表示后一种重要的数据获取和表示方式。对于数据Xn×n=[x1,x2,…,xn],xi∈Rn,可以被字典A=[a1,a2,…,am]的原子线性表出[14],即
X=AZ
式中Z=[z1,z2,…,zm]为X在字典A下的表示系数,字典A通常是过完备的。在特定情况下,低秩矩阵恢复和稀疏表示等价,此时上式即为在某些特定的字典下求解数据的稀疏表示。稀疏表示可能无法捕捉到数据X的整体结构,因此我们转而求解下述优化问题

模型的解Z为X在字典A下的低秩表示。上述模型计算量大,求解困难,可通过松弛得到如下等价优化问题
式中‖·‖*为矩阵的核范数。取矩阵X作字典,从而有
其中X的元素可以当作自身的低秩表示。通常得到的图像受到噪声等因素的影响,需要放松上述模型中的等式约束,即
(4)

得到优化问题(4)的解(Z*,E*)后,通过X-E或者XZ*即可恢复出原始的数据X[15]。
因为rank(XZ)≤min(rank(X),rank(Z)),所以简称XZ为低秩部分,E为稀疏部分。低秩部分包含了图像的大部分信息,稀疏部分主要是一些高频细节信息。
2.2 算法的提出
现实得到的图像会受到噪声的污染,因此式(1)图像的退化模型应该修改为
Y=SHX+n
(5)
式中n为噪声[16]。此时式(2)不再成立,对于包含少量信息的低分辨率图像块,为避免冗余字典的出现,应该选用较少原子的字典来表示,因此放松约束,不再要求高低分辨率字典原子数目相同。假设Dl为欠完备字典,Dh为过完备字典,在此假设基础上,Peleg构建了一个基于稀疏表示的统计预测模型(SPBSR)来实现单幅图像的超分辨率重建[17]。
假设αh、αl为高、低分辨率图像的稀疏表示,sh、sl为对应的稀疏表示模式,其中

(6)
λ是满足
的最大阈值,其中τ是预先指定的稀疏表示精度。在给定sl和αl的情况下,有
(7)
式中:bh∈Rmh是高分辨率稀疏模式的偏差向量;whl∈Rmh×ml是高低分辨率稀疏模式间的互动矩阵;Φ(z)=(1+exp(-2z))-1是激活函数。
进一步,在给定sl和αl时使用最小均方差估计,有

(8)
综合上述分析,本文给出一种新的图像超分辨率重建算法。首先,对退化图像Y进行低秩恢复,得到低秩部分L和稀疏部分S,即Y=L+S。然后,对于低秩部分,采用上述预测模型进行稀疏重建,这里低分辨率字典Dl为欠完备字典,高分辨率字典Dh为过完备字典,不需要高、低分辨率字典尺寸相同。相比HR图像,LR图像在退化过程中丢失了大量细节信息。为了确保重建模型的稳定性,本文采用多层串联算法来逐步提升图像的质量。Bagon提出的M级放大因子序列为1 重建模型的每一层与基本算法形式相同。在训练阶段,从HR图像生成一串质量递增的图像,使用双三次滤波,并设置降采样因子为如下序列 q/q1>q/q2>…>q/qM=1 来得到一个M层的图像金字塔,接着进行双三次插值处理,将图像恢复到原始尺寸。对训练样本的HR图像使用标准差序列为 σ1=σ/q1>σ2=σ/q2>…>σM-1=σ/qM>σM=0 的高斯滤波,得到一组模糊图像。 综合上述分析,本文提出融合低秩和稀疏表示的图像超分辨率重建算法如下: 输入:低分辨率图像zl,放大倍数q,模型参数Dl、Dh、Chl、bh、whl通过线下学习得到 步骤: (1)对zl进行低秩恢复(low rank represent,lrr)得到[a,b]=lrr(zl,0.01); (2)对zl进行q倍双三次插值得到yl,其中zl=zl·a; 实验在Intel Core i5-4200U 2.53 GHz计算机、Matlab R2016b软件环境下进行。实验设置重建环境为大小5×5、标准差1.5的高斯滤波,降采样因子为3,噪声为Matlab中imnoise函数产生的高斯噪声,均值为0,方差为0.01。 现实环境中得到的图像通常都会有一定的噪声污染。以双三次插值算法为例,选用lena图像和foreman图像,分别在无噪声和使用Matlab的imnoise函数添加的均值为0、方差为0.01的噪声环境下进行对比实验,表1记录了重建图像的峰值信噪比(用Rsn,peak表示),图1给出了SPBSR算法重建性能的直观显示。 表1 插值重建性能 由表1可知,在噪声环境下重建图像的峰值信噪比大幅下降,同时图1也表明,插值算法重建出的图像趋于模糊,丢失了部分细节信息,并且在噪声环境下算法的性能退化更加剧烈,说明噪声极大地影响了算法的重建性能。 (a)原始图像 (b)无噪声插值重建图像 (c)含噪声图像 (d)含噪声插值重建图像图1 图像插值重建性能对比 为了抑制图像噪声对重建过程的影响,对于待重建图像zl,首先进行低秩恢复得到低秩和稀疏部分。从低秩恢复的模型出发,E为稀疏矩阵,包含图像的部分高频信息,因为噪声也是高频信息,所以会被吸收到E中。以foreman图像为例,低秩恢复的直观效果如图2所示。 (a)原始图像 (b)低秩恢复图像(λ=0.15)图2 foreman图像低秩恢复示意图 图2表明,低秩恢复的图像视觉效果更好,因此将低秩恢复操作融合到图像的超分辨率重建是合理可行的。首先,对待重建的低分辨率图像zl进行低秩矩阵恢复,得到低秩部分和稀疏部分;然后,将低秩部分插值重建到原始图像尺寸,利用学习到的高低分辨率字典对进行稀疏重建,得到最终的重建图像。为了比较重建算法的优劣,选用lena、butterfly、pepper、foreman、pens图像,分别采用双三次插值、ScSR、MSPB[18]和SPBSR算法进行对比实验,并选用峰值信噪比作为客观评价指标,实验结果见表2,各算法重建性能的直观对比见图3(为了比较算法的性能,放大了图像的部分细节信息)。 表2 不同算法的重建性能对比 (a)双三次插值 (b)ScSR算法 (c)MSPB算法 (d)SPBSR算法 (e)本文算法 (f)原始图像图3 不同算法重建图像的视觉效果展示 由表2可以看出,本文算法的性能最优,具有最高的峰值信噪比,说明在噪声环境下对低分辨率图像进行低秩恢复操作是切实有效的。由图3可以看出:双三次插值重建对图像噪声几乎没有作用,重建结果相当模糊,缺失了大量的高频细节信息;ScSR算法对噪声有一定的抑制,较之于插值算法性能有所提升,重建出了原始图像的大部分信息,但是重建图像的边缘不够清晰,有些模糊;MSPB算法的重建图像对于噪声的抑制作用明显,但是重建出的图像带有阴影,影响了视觉效果;SPBSR算法的重建图像具有不错的细节信息,不再趋于模糊,但是颗粒感强烈,影响视觉;本文算法加入了低秩恢复操作,提升了算法对噪声的抑制作用,因此重建图像边缘清晰,视觉效果更好。 由表2还可以看出,MSPB算法和本文算法的性能相近。为了进一步比较各种算法的性能,对比了各算法的运行时间,见表3,可知本文算法与SPBSR算法耗时相近;MSPB算法耗时最多,是本文算法的十多倍;ScSR算法耗时次之,是本文算法的5倍左右;双三次插值算法耗时最少。尽管MSPB算法与本文算法性能相近,但考虑其运行效率的限制,不具备实时性;双三次插值虽然运行效率最高,但其重建性能低下;SPBSR算法与本文算法的运行效率相近,但其重建性能不如本文算法。 表3 不同算法的图像重建时间对比 为了达到更好的重建效果,对于低秩恢复操作取不同的λ值进行对比实验,结果见表4,可知λ=0.01时效果最好。表5给出了本文算法与SPBSR算法的性能比较结果。 表5 本文算法性能提升统计 表3的数据表明,加入低秩恢复操作后,本文算法的运行时间减少,并且算法性能也有提升。但是,由于图像的边缘、纹理等细节信息与噪声同属高频信息,因此稀疏部分同时包含有原始图像的部分高频信息,并且这部分信息没有被用来重建原始图像。图2证实了这一情况:原图背景中的一些黑色斑点在进行低秩恢复操作时没有被恢复出来,而是被当作污染去除了,因为低秩恢复的目的就是从受到污染的数据中恢复出干净的数据。以Child图像为例,低秩恢复的视觉效果如图4所示。为了方便显示,稀疏部分进行了对比度增强,可以看出其中包含有很多的细节信息,而这部分信息对于超分辨率重建是至关重要的,因为超分辨率重建的关键就是重建原始图像丢失的高频信息。 (a)原始图像 (b)低秩恢复图像 (c)稀疏图像图4 低秩恢复误差显示 以parrots图像为例,将原始图像与重建图像的视觉效果进行对比,如图5所示,可见重建图像的背景也趋于模糊,同时重建图像的边缘不够清晰。图像重建算法的优劣,由重建出的信息量决定。从图4可以看出,低秩恢复操作得到的稀疏部分除了噪声外,还含有原始图像的一些边缘细节信息,将这些高频信息加入到重建过程,将会进一步提升算法的重建性能。 (a)原始图像 (b)重建图像图5 parrots重建图像与原始图像对比 针对图像超分辨率重建算法收敛速度慢、易受退化图像噪声影响等问题,本文将低秩矩阵恢复与稀疏表示相结合,提出了一种新的图像超分辨率重建算法。对于待重建的退化图像,首先进行低秩恢复,得到含有原始图像大部分信息的低秩部分和主要由噪声组成的稀疏部分,然后对低秩部分利用学习到的高低分辨率字典对进行稀疏重建。对退化图像进行低秩恢复后再重建,一是抑制了图像噪声对重建过程的影响,二是提升了算法的效率。实验结果表明,本文算法不仅在运行速度上得到了提升,而且图像的视觉效果更佳,更加清晰,相比SPBSR算法,本文算法的峰值信噪比指标平均提高了4 dB。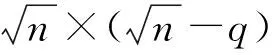
2.3 融合低秩和稀疏表示的超分辨率重建算法



3 实 验












4 总 结
