板翅式换热器瞬态法数值模拟与实验研究

杨永斌, 厉彦忠,2, 司标

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.西安交通大学动力工程多相流国家重点实验室, 710049, 西安)

板翅式换热器广泛应用于空分、航天、化工等领域,由于其复杂性,翅片通道的传热因子往往难以确定,板翅式换热器换热性能的研究方法主要分为传统的稳态研究方法和瞬态方法,传统稳态法主要有牛顿换热公式直接求得法、等雷诺数法、威尔逊法[1]、等换热系数等方法。在传统稳态法中,以Kays等的实验最为经典,他们通过风洞实验测试了40多种类型翅片的流动换热性能,并将结果绘制成表格[2]。Wieting通过实验研究了雷诺数低于10 000的翅片通道内的流动换热性能,发现了翅片厚度对此工况范围内的翅片性能影响较大[3]。Mullinsen等对板翅式换热器做了可视化的实验,观测到了板翅式换热器在不同雷诺数下的流态情况[4]。Joshi等对板翅式换热器做了相关实验,整理了相应的经验关联式[5]。董军启等完成了16种用于车辆机油冷却的板翅式换热器的实验研究,根据实验结果给出了相应的预测关联式[6]。李媛等通过风洞实验和数值模拟研究了不同类型的板翅式换热器翅片的表面特性[7]。张哲等通过数值模拟研究了影响导流片出口物流分配不均匀的因素[8]。康蕊等通过数值模拟研究了轴向导热对板翅式换热器性能的影响规律[9]。牛顿换热公式直接求得法需直接测取换热器壁温,对于复杂结构的壁面,测量困难、误差大。等雷诺数法要求换热器两侧通道几何相似,同时需要调节两侧通道内流体的流速与温度,在实际应用过程中很难控制。威尔逊法要求换热器两侧流体换热系数差距较大,对于板翅式换热器,工程应用中通常是液体与液体或者液体与蒸汽之间的换热,换热系数差距并不大。等换热系数法假设冷热流体的对流换热系数相等,获得测试数据后进行曲线拟合,该方法实验设备复杂,控制极为困难。采用稳态法对换热器进行测量时仅限于传热单元数较小的设备,当传热单元数较大时,采用稳态法均会产生较大的误差,稳态法实验周期长、效率低、耗资较大。

因此,本文引入Mullisen等提出的瞬态单吹技术[10],此方法根据有限差分理论采用数值方法对所建立的数学模型进行求解,并考虑了固体纵向导热影响。瞬态技术优点显著,采用单流体,实验设备简单,无需壁温测量,测量精度不受单元数的限制,实验周期短,可快速获得板翅式换热器的性能参数,节省了大量的财力物力。本文主要探索采用该方法预测板翅式换热器翅片通道的换热性能的可行性、准确性,为瞬态实验方案及数值模拟奠定理论基础,并为后期工程设计提供有价值的预测方案。

1 瞬态测试技术原理

1.1 瞬态法理论基础

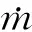
图1 瞬态换热微元体示意图

相应的无量纲微分方程为

(1)

式中:τ为时间。

Schumann(1929年)得到的分析解为[11]

(2)

(3)

式中:Tf1为流体入口温度;Tf2为流体出口温度;Ti为初始时刻温度;U为流体的传热单元数;K为总传热系数;F0为总传热面积;W为流体的质量流量。可得Tf2=f(Ti,Tf1,U,τ),通过实验可以测得初始温度Ti、流体入口温度Tf1及出口温度Tf2随τ的变化曲线,然后将实验得到的Tf2与理论计算得到的出口温度曲线配比来确定单元数,进而可求得平均表面传热系数h。瞬态换热实验方法按不同的配比方法分为直接配比法、选点配比法和最大斜率法,按照数学模型中不同的入口温度,函数分为阶跃函数法、部分阶跃法、周期函数法和指数函数法[12-17]。

上述方法都是在简化的数学模型中,通过求解微分方程分析解与实验结果比较来得出所求的换热系数,每种方法只适用于各自的特定条件,而且计算精度受到简化模型的制约。为了改善瞬态实验的精度和适用范围,本文运用瞬态单吹技术,考虑了气体轴向导热及气体比热容的影响。

1.2 瞬态实验的物理模型处理

板翅式换热器结构简图如图2所示。对板翅式换热器作如下简化假设:①介质沿板翅式换热主流方向的长度远大于翅片通道截面尺寸,因此将三维问题简化为沿流动方向的一维问题处理;②实验中空气温升较小,仅从环境温度提升30 K左右,可认为流、固体的热物性不变,每次测试针对固定雷诺数工况,可认为流动是稳定均匀的;③对换热器蓄热芯体做绝热处理,可认为换热器芯体与外界绝热;④在对空气进行加热前测量初始温度场,起始时刻为环境温度,可认为初始时刻流体与换热器芯体处于均匀的温度场中。简化后建立物理换热模型如图3所示。

根据图3,分别对上、下隔板,翅片及空气列能量守恒方程并将傅里叶定律、牛顿冷却定律代入,可得控制方程

(4)

(5)

(6)

(7)

(8)

式中:ρ为密度;δ为厚度;λ为导热系数;C为比热容;T为温度;uf为流速。

相应的初始条件和边界条件为

Ts1(X,t=0)=Ts2(X,t=0)=

Ts3(X,t=0)=Ts4(X,t=0)=T0

Tf(X=0,t)=Tin(t)

Tf(X=L,t)=Tout(t)

式中:T0为初始温度;Tin(t)、Tout(t)分别为实测翅片通道入口和出口处流体温度。

图2 板翅式换热器结构简图

图3 翅片通道与流体之间物理传热模型

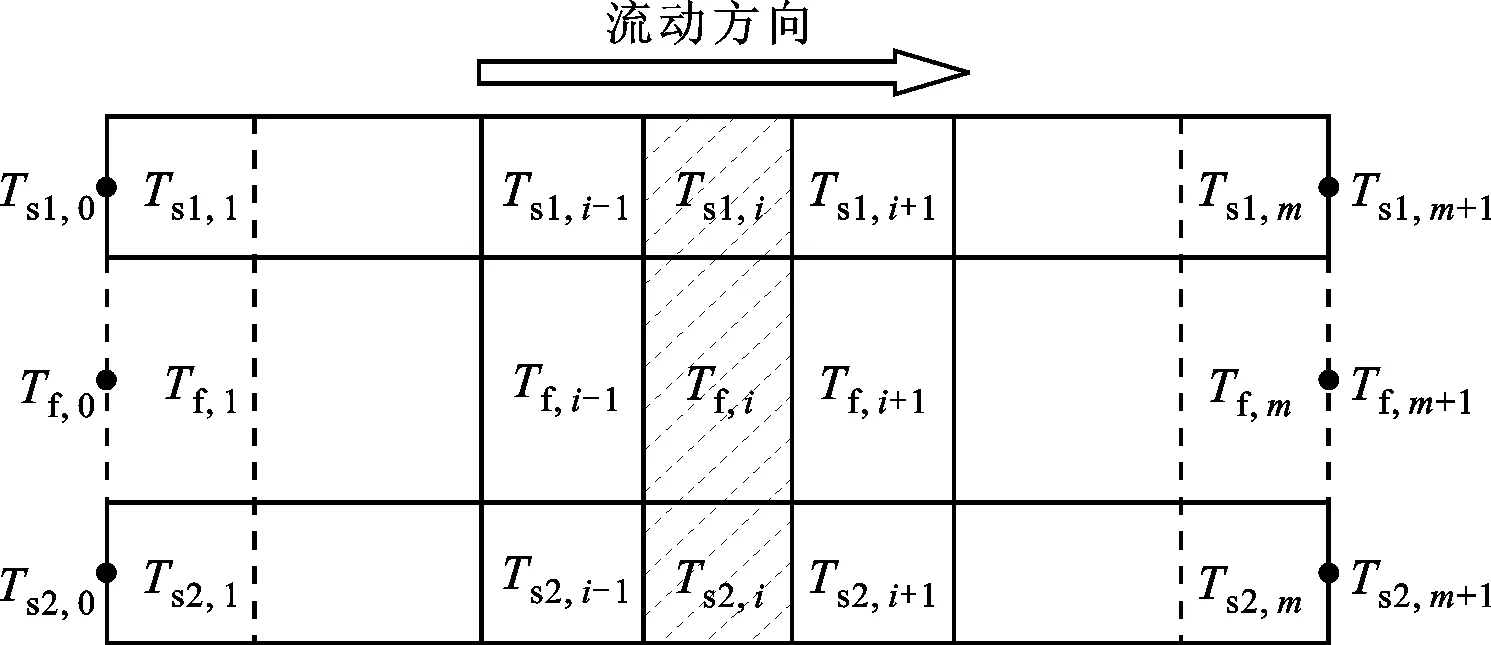
图4 上下隔板与空气层离散模型

用内节点法离散化后的隔板与空气层换热计算区域模型如图4所示。实验段沿流向被分成了m个控制容积,进出口边界分别为0和m+1,即i的取值范围。将整个实验持续的时间分成n+1个时层,对上述的微分方程在一个控制容积和一个时层上进行二重积分,对未知量T的分布灵活选用不同的离散方法就能得到不同格式下的能量守恒离散方程,可以求出离散化的初始条件和边界条件。再将离散方程整理成三对角矩阵形式,运用TDMA算法[18]对方程进行求解,计算流程如图5、6所示。

图5 整体计算流程图

图6 单个时层计算流程图

本文采用Visual Basic语言进行编程计算,计算程序主要包含4个窗体、1个公共模块和2个类模块。分别对几何参数、热力参数、数据处理进行设置后,程序开始迭代计算,计算结束后,程序自动将计算结果以Excel表格的形式输出。计算结果中包含雷诺数、普朗特数、平均对流换热系数、换热因子f、运动黏度及不同时层、空间层的温度场分布等。

2 平直型板翅式换热器的瞬态性能数值模拟与实验验证

2.1 建模与网格划分

本文采用47PZ3002型翅片形式的板翅式换热器,换热器通道长度为300 mm,翅片通道结构如图7所示。

图7 翅片通道结构示意图

由于对整个换热器进行数值模拟难以实现,因此取单个换热通道进行模拟,考虑进出口段对模拟结果的影响,根据文献[19]的结论,不同雷诺数下平直翅片模型入口段长度的计算公式为

Le=0.05RePrDh

(9)

(10)

式中:Re、Pr为雷诺数和普朗特数;Dh为当量直径。在Gambit中进行网格划分,如图8所示。

图8 在Gambit中建模及网格划分示意图

对于板翅式换热器,其换热性能及流动性能可以通过换热因子j与摩擦因子f反映,j因子、努塞尔数、f因子的表达式[20-22]分别为

(11)

(12)

(13)

式中:ΔP为换热器进出口压差;L为有效换热长度;G为空气流量。

在计算前进行了网格无关性验证,在Re为3 000的工况下,当网格数达到12 067 380时,j因子变化了1.47%,f因子变化了3.38%,已完全符合计算要求,因此后期数值计算都采用以上网格密度作为标准,结果如图9所示。

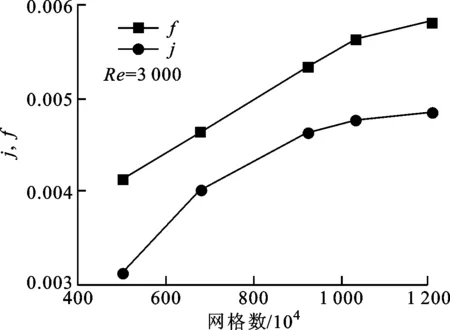
图9 网格无关性验证

2.2 基本方程与数值模拟的设置

本文数值模拟中的方程主要包括质量方程、动量方程以及能量方程。在每个模拟工况下,认为空气密度不随时间变化,则连续性方程、动量方程和能量方程为

(14)

(15)

(16)

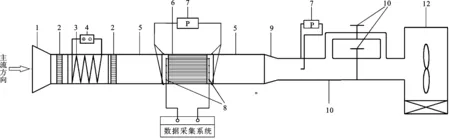
1:入口段;2:整流栅;3:电加热器;4:电功调整器;5:稳流段;6:实验件;7:压差变送器;8:热电偶;9:过渡段;10:出口段;11:阀门;12:变频风机图10 实验风洞系统图

式中:μ为动力黏度;Su、Sv、Sw为动量守恒方程的广义源相;ST为黏性耗散热能。

本节所述控制方程为fluent软件中瞬态数值模拟模型对应的通用控制方程,上节中的控制方程为瞬态模型推导得到的能量控制方程。对于雷诺数为500～3 000的工况条件,换热器内的流动从层流一直过渡到湍流,因此雷诺数在500～1 800之间时选择Laminar模型,雷诺数在1 800～2 500之间时选择k-omega模型,雷诺数在2 500～3 000之间时选择低雷诺数k-epsilon模型,算法均采用SIMPLE-C算法。

入口根据所模拟雷诺数工况给定相应的速度,入口温度为实验测量温度,通过UDF模型编入Fluent中进行计算。出口为压力出口,上下隔板的外壁面为绝热边界条件,流固接触面为耦合边界条件,翅片通道两侧为对称边界条件,初始温度为实验测得的温度初场。采用非稳态计算模型,时间步长为0.1 s,单个时间步长内最大迭代步数为20。能量方程残差为10-10,其他残差均为10-6。

2.3 瞬态单吹实验验证

瞬态实验系统实际上是一个开路低速风洞,实验段为板翅式换热器蓄热芯体,换热器外表面做绝热处理[23-26],变频风机采用吸风式风洞系统,实验系统如图10所示。气流经入口段后进行一次整流,通过电加热升温后再次整流,流经稳定段后进入换热器进行换热,换热结束依次经稳定段、收缩段和出口段直至被风机吹入环境中。

实验段进出口截面附近分别布置了温度和压力测点,用于测量进出口流体温度以及实验段空气压降。进出口流体温度测量由热电偶完成,热电偶均匀地分布在整个流通截面上,使用瞬态数据采集系统对实验数据进行采集,压降由差压变送器读取。此外,在风洞出口段前端布置了毕托管测速器,用于监测风洞系统流量,进而通过变频系统调节,来预测工况流量。经误差分析,整个测量系统对温度的测量误差低于0.41%,对压力的测量误差低于4%。实验步骤如下:

(1)开启数据采集系统和风机,调整变频旋钮至所需流量;

(2)随着来流空气对蓄热芯体的冲刷,流体固体温度趋于一致;

(3)监视进出口截面温度值、实验段压损,待两者均不再变化时记录下压差数据,压力场测量完成;

(4)监视温度初场,待实验段温度达到稳定状态时迅速打开加热器电源,开始加热实验段入流空气;

(5)连续监视并记录流量大小、进出口截面空气温度随时间的变化曲线,直到出口截面处空气温度趋于渐近值为止,整个瞬态测量过程结束;

(6)根据工况改变流量,重复步骤(1)～(5),最终完成对不同Re下换热器的热力、阻力特性测试。

本文对实验台进行了验证,瞬态法获得的j因子与f因子和文献[2]的稳态实验值对比如图11、12所示。选取4个工况点进行验证,可知瞬态单吹实验获得的j因子与f因子和文献[2]的实验值相比,整体趋势一致,平均偏差分别为5.18%、6.21%,可以认为在雷诺数为500～3 000的范围内,瞬态单吹实验平台对板翅式换热器的热力阻力性能测试结果可靠。

图11 j因子和文献[2]稳态实验对比

3 结果对比及分析

雷诺数为1 500的工况下,运用CFD模拟和瞬态单吹实验获得的换热器进出口温度场随时间的变化如图13所示。由图13可知,数值模拟与实验结果十分吻合,且最大偏差为1%,因此可以认为,CFD数值模拟结果对出口温度场的预测可靠。

图13 进出口温度场随时间的变化

雷诺数为1 500的工况下,换热进行到第9 s时换热器内不同位置处空气温度场的分布情况如图14所示。由图14可知,从换热器入口到出口,空气层温度逐渐降低,符合实际的换热规律,且CFD模拟结果与实验结果偏差低于2%。

图14 同一时刻不同位置的温度分布

图15 j因子与Re之间的关系

图15给出了运用瞬态法获得的47PZ3002型板翅式换热器换热因子j随雷诺数的变化情况,可知数值模拟与瞬态单吹实验得到的结果具有较高的一致性,偏差不超过10.7%。

图16给出了换热器进出口压降随雷诺数的变化情况。由图16可知,随着雷诺数的增加,换热器进出口压降逐渐增大,即流动阻力增加,与实际情况相符合。实验值与模拟值之间的误差较小,模拟结果可以预测实际换热器的压降情况。

图16 进出口压降与Re之间的关系

图17给出了f因子随雷诺数的变化情况,可知模拟值与实验值的变化趋势一致,偏差低于13%。随着雷诺数的增加,f因子逐渐减小,当雷诺数小于2 000时变化显著,当雷诺数大于2 000时,f因子变化缓慢。

图17 f因子与Re之间的关系

4 结 论

(1)本文采用的瞬态单吹技术对47PZ3002型板翅式换热器的性能预测是可靠的。

(2)雷诺数为500～3 000时,应用CFD模拟的换热器出口温度场与实验值高度吻合,偏差低于3.1%,可以准确预测换热器出口温度;瞬态技术对换热器内不同位置的温度场预测十分准确,实验值与模拟值变化趋势一致,偏差低于2%。

(3)运用瞬态技术对j因子预测的模拟值与实验值随雷诺数变化趋势一致,在雷诺数低于2 000时,随着雷诺数的增加,j因子逐渐减小,且在雷诺数较小时变化显著,当雷诺数约为2 000时,板翅式换热器内的流动由层流过渡到湍流,换热增强,可知j因子随雷诺数的增加呈现上升趋势,当雷诺数大于2 000时,j因子随雷诺数增加逐渐增大,最终出现了缓慢下降的趋势。此外,模拟值与实验值之间的平均偏差为4.4%,最大偏差不超过10.7%。

(4)f因子预测的实验值与模拟值之间的最大偏差为13%。整个工况范围内,随着雷诺数的增加,f因子呈下降趋势。当雷诺数小于2 000时,f因子随雷诺数增加呈现下降趋势,跨过层流区即雷诺数大于2 000时,随着雷诺数增加f因子呈缓慢下降趋势。

因此,采用瞬态技术研究板翅式换热器通道的流动、传热特性是可行的,与传统稳态技术相比,瞬态技术特点鲜明、测量简单、方便快捷、效率高,可快速获得板翅式换热器的性能参数,精度高,且不受传热单元数的影响。借助CFD强大的分析计算能力,可实现板翅式换热器热力阻力性能的瞬态模拟,用数值手段代替瞬态实验,能够进一步提高研究效率,节约设备投入和时间成本。