限流细长孔板阻力特性实验研究与关联式评价

2018-07-25胡娟娟李会雄盛天佑倪士尧王耀东谢恩飞

西安交通大学学报 2018年7期

胡娟娟, 李会雄, 盛天佑, 倪士尧, 王耀东, 谢恩飞

(1.西安交通大学多相流国家重点实验室, 710049, 西安; 2.中国核电工程有限公司, 100000, 北京;3.深圳中广核工程设计有限公司, 518000, 广东深圳)

作为流动系统中常见的节流降压装置,孔板以结构简单、工作可靠、易于安装、方便维护、价格低廉等优点,广泛应用于工业管道系统、液压系统与燃油喷雾系统等[1-4]。细长孔板通常指长径比大于4的孔板[3],能在流动系统中产生更大的压降,在局部压力控制和流量控制中有重要作用[5]。在核电厂反应堆的冷却剂流动与控制系统中,限流细长孔板具有限流和保压双重作用,是核反应堆冷却系统中的核心部件之一,对反应堆一回路冷却系统的工作性能和安全性有显著影响。

相较于普通的限流孔板,流体流经限流细长孔板时会产生更大的压降,从而产生更显著的限流、降压效果。然而,当孔板下游压力低于流体的饱和压力时,会伴有空化现象发生,可能引起设备振动、产生噪声,并可能导致设备不能正常使用[6-7]。因此,仔细研究限流孔板的阻力特性,探索限流孔板下游流体压力的动态变化规律,对孔板的设计与合理应用都具有重要意义。

目前,国内外学者已经针对孔板阻力特性展开了广泛的研究。Jankowski等认为,孔板的压降可以分为孔板进出口处的局部损失产生的压降和流体在孔内的沿程阻力损失产生的压降,并以此为基础建立了计算孔板流量系数与压降的计算模型[8]。但是,该模型适用范围非常有限,仅适用于长径比小于15以及孔内雷诺数小于105的情况。Nakayama对长径比范围为0.799～16.520的一系列孔板的阻力特性进行了实验研究,并得出了孔板阻力计算关联式,适用的雷诺数范围为550～700[9]。Yu等研究了孔板背压对孔板流量系数以及阻力的影响,结果表明孔板阻力与孔内工质流速的平方成正比,孔板背压会影响阻力系数的大小,同时得到了孔板阻力关联式,适用的长径比范围为5.0～6.4,孔内雷诺数范围为1.60×104～1.32×105[10]。

纵观以往的相关研究结果可以发现,关于孔板阻力特性的研究主要针对薄孔板以及长径比相对较小的厚孔板进行。Chisholm提出,当工质流经一定长度的孔板时可能会出现两种流态:孔板较短时,流体流动过程中的缩颈会出现在孔板外部;孔板较长时,缩颈会出现在孔板内部,之后流动逐渐恢复,流体占据整个流动通道,直到突扩后进入下游管道[11]。由此可见,在长径比不同的孔板内,流体的流动形态也有较大区别。因此,对大长径比的孔板阻力特性进行研究,并提出相应的计算关联式是十分必要的。

本文以长径比为5～70的限流细长孔板为研究对象,在高温高压条件下,对其阻力特性进行了详细的实验研究;以实验数据为基础,评价了已有的孔板阻力计算关联式的预测性能,并在此基础上提出适用于大长径比细长孔板内高雷诺数流体流动阻力的新计算关联式。

1 实验系统

本实验在西安交通大学动力工程多相流国家重点实验室的高压汽-水两相流实验台上进行。实验以去离子水为工质,对不同几何参数的细长孔板在不同工况下的阻力特性进行了研究。实验系统如图1所示。

实验过程中,水箱中的去离子水经高压柱塞泵加压后进入下游,通过主路和支路流量调节阀的调节,使主路流量达到指定流量与压力;通过预热段将主路的水加热到指定温度,然后流经限流孔板实验段,再经冷凝器散热达到室温后重新回到水箱。

1:水箱;2:高压柱塞泵;3:流量调节阀;4:流量计;5:再生式换热器;6:预热段;7:孔板特性实验段;8:耐高压阀门;9:冷凝器图1 实验系统简图

图2给出了实验段的局部放大图。在孔板上下游分别布置有热电偶与罗斯蒙特压力表,用来监测孔板前后工质的温度和压力。为防止孔板入口效应与出口效应对孔板阻力测量的影响,孔板上游压力测点设置于距离孔板入口500 mm的位置,孔板下游压力测点分别设置于距离孔板出口350、650 mm的位置,通过两台压力表测量结果的对比来判断细长孔板下游背压恢复情况。实验过程中反复调节系统中主路阀、旁路阀开度,以确保系统达到稳定时孔板背压为2.8 MPa,此时测得孔板上游压力,二者之差即为孔板阻力。

图2 实验段测点布置图

实验过程中需要测量的主要参数有通过孔板的流量、孔板进出口压力、工质进出口温度。各实验参数的范围:质量流量Q为0.5～4.5 t/h;孔板压力p为0～32 MPa;工质入口温度Tin为0～170 ℃。

此外,为了解孔板内流体的流动状态,孔内流动雷诺数Re也为一个需要实时计算、监测的间接变量。其定义式为

(1)

式中:ρ、V、μ分别为孔内工质的密度、流速及动力黏度,均以孔内工质进出口平均温度为定性温度时求得;d为孔径;Re的范围为1.5×105～3.0×106。

实验中孔板进口温度远低于对应压力下的饱和温度,以防止因受热不均导致工质发生局部闪蒸而干扰实验研究。值得指出的是,由于实验所采用的各孔板的几何尺寸差别较大,因此不同孔板的实验参数范围不完全相同。为了研究细长孔板各几何因素对其阻力特性的影响,本文实验设计了9组不同尺寸的孔板,表1给出了实验孔板的绝对尺寸与相对尺寸的范围。

表1 孔板的绝对尺寸与相对尺寸的取值范围

为方便描述孔板尺寸,本文选取了一组参考孔板(d=d0,L=L0,D=D0),并以参考孔板的孔径d0作为参考尺寸,由此实验孔板各几何尺寸都可表示为d0的倍数的形式。

2 实验结果与分析

2.1 管道直径的影响

为研究管道直径对限流细长孔板阻力特性的影响,选用孔板直径均为d0、孔板长度均为50d0、管道直径不等的3组孔板进行了实验研究。图3给出了工质入口温度分别为50、110和170 ℃时,不同管道直径下各细长孔板的阻力随质量流量的变化趋势。

(a)工质入口温度为50 ℃

(b)工质入口温度为110 ℃

(c)工质入口温度为170 ℃图3 管道直径对限流细长孔板阻力特性的影响

由图3可以看出:其他条件相同时,随着管道直径的变化,孔板阻力随质量流量的变化并不明显,阻力曲线近乎重合。这是因为对于限流细长孔板来说,其沿程阻力损失占总损失较大的份额,与之相比,孔板入口处突缩、出口处突扩造成的局部阻力损失相对较小,基本可以忽略。由此可见,对于细长孔板这种降压、限流装置来说,阻力受孔板本身结构的影响较大,受与其相连管件的结构参数的影响则较小。

2.2 孔板长度的影响

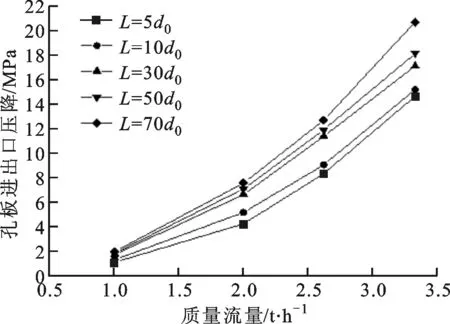
为研究限流细长孔板长度对其阻力特性的影响,选用管道直径均为7d0、孔板直径均为d0、孔板长度不等的5组孔板进行了实验研究。图4给出了工质入口温度分别为50、110和170 ℃时,不同长度的细长孔板的阻力随质量流量的变化趋势。

(a)工质入口温度为50 ℃

(b)工质入口温度为110 ℃

(c)工质入口温度为170 ℃图4 限流细长孔板长度对其阻力特性的影响

由图4可知:其他条件相同时,随着限流细长孔板长度的增加,阻力呈现增大的趋势;质量流量越大,阻力随孔板长度增加而增大的趋势越明显。当不考虑孔板入口处突缩截面与出口处突扩截面的流动时,孔内流动可以近似为圆管内流动,流动的沿程阻力损失为[12]

(2)

式中:f为沿程损失的阻力系数。

由式(2)可以看出,圆管的沿程阻力损失与其长度成正比,与管内工质流速的二次方也成正比,这一规律与图4所示实验结果相吻合。

2.3 孔板直径的影响

为研究限流细长孔板直径对其阻力特性的影响,选用管道直径均为7d0、孔板长度均为50d0、孔板直径不等的3组孔板进行了实验研究。

图5给出了工质入口温度分别为50、110和170 ℃时,具有不同孔径的细长孔板的阻力随质量流量的变化趋势。由图可以看出,孔板直径越小,阻力越大,且孔板直径对阻力的影响十分显著。

(a)入口工质温度为50 ℃

(b)入口工质温度为110 ℃

(c)入口工质温度为170 ℃图5 限流细长孔板直径对其阻力特性的影响

孔板直径对其阻力特性的影响主要体现在两个方面:一是由于管道沿程阻力损失与管道直径成反比(如式(2)所示),管道直径越小,沿程阻力损失越大;二是当质量流量一定时,孔板内流速与直径的二次方成反比,而式(2)表明管道沿程阻力损失与流速的二次方成正比。两个因素的综合作用,使得质量流量一定时,管内沿程阻力损失与孔板直径的关系为Δp∝d-5。因此,与管道直径和孔板长度相比,孔板的直径对其阻力特性的影响十分显著。

3 孔板阻力计算关联式的评价与提出

3.1 现有阻力关联式预测能力的分析与评价

从20世纪60年代至今,国内外一些专家学者已相继对孔板阻力特性展开了大量研究,并提出了一系列计算孔板阻力的公式。

针对厚孔板内流动,Chisholm提出的阻力计算公式[11]为

(3)

L/d≥0.5

式中:σ=(d/D)2为孔板与管道截面积之比;σc=1/[0.639(1-σ)0.5+1]为突缩系数。可以看出,式(3)充分考虑了管道截面与孔板截面尺寸差异(即d/D)对孔板阻力的影响,但并未考虑L的影响。

Fried等提出了针对孔板类结构的通用的阻力计算式[13]

(4)

式中:ξ为阻力系数;ξ′为取决于孔板进口结构的参数,本文ξ′取0.03;τ为孔板外形调整系数,对于进口形状为圆角或者坡口的情况,可以近似表达为τ≈2ξ′0.5;ξfr为孔内沿程阻力系数,对于孔板入口形状为坡口或圆角的孔板,ξfr=0。

以式(4)为基础,刘长亮等提出了针对单级无斜角孔板与单长孔孔板的阻力计算式[1]

(5)

可以看出,式(4)(5)都是通过确定ξ来求得孔板的阻力,其差别在于式(5)在式(4)的基础上考虑了L对阻力的影响。

Nakayama提出了针对长孔板流量系数与阻力的计算公式[9]

(6)

0.799

式中:Cd为孔板流量系数。

Yu等在对喷嘴流量特性进行研究时,提出了如下阻力计算公式[10]

(7)

5.0

Jankowski等建立了孔板流量系数与阻力的计算模型,并以此为基础提出了如下计算公式[8]

(8)

L/d<15;Re<105

式中:Cd,s为孔板内部流量系数;f为孔内沿程阻力系数,取值同ξfr。

对比式(6)～(8)可以看出,式(6)～(8)均是通过确定孔板流量系数来求得孔板阻力,其中式(6)(7)中Cd的表达式形式相同,但对应系数的差距很大。

图6a～6f给出了各关联式预测值与本文实验数据的对比结果。为进一步定量评价各关联式的预测精度,本文采用平均相对误差εMAD与相对误差绝对值的平均值εMARD表示预测结果与实验结果的相对偏差,采用Ψ表示相对误差落入一定误差带内的工况数占工况总数的百分比,相关定义为

(9)

(10)

式中:y(i)cal为第i个工况的关联式计算值;y(i)exp为第i个工况的实验值;N为工况总数。各关联式的评价结果如表2所示。

结合图6和表2可以看出:文献中的各关联式对本文实验结果的预测并不准确,且误差的绝对值随实验值的增大而增大。式(3)(5)(8)的预测值整体偏大,其中式(5)的εMAD高达49.55%,落入±30%误差带的数据仅为17.22%,同时式(3)(8)的相对误差落入±30%误差带的也不足80%;式(4)(6)(7)的预测值整体偏小,式(4)落入±30%误差带的数据占总数据的78.88%,预测精度不高;式(6)(7)的预测精度尚且可以,落入±30%误差带的数据超过90%,但预测值普遍偏低。因此,需要以本文实验数据为基础,对已有关联式进行修正,开发出适用范围更广、计算结果更精确的细长孔板阻力计算关联式。

(a)式(3) (b)式(4) (c)式(5)

(d)式(6) (e)式(7) (f)式(8)图6 关联式预测值与实验数据对比图

表2 关联式评价结果

3.2 新阻力关联式的提出

根据已有的研究结果可知,影响孔板阻力特性的主要因素有孔板的几何结构与孔板内工质特性[14]。孔板几何参数主要包括孔板长度L、孔板内径d、与孔板连接的管道内径D;孔板内工质的特征参数主要包括流速、密度、动力黏度等,通常采用孔内雷诺数Re来描述。由本文实验结果可知,管道直径对限流细长孔板的阻力影响可以忽略不计。

参考式(6)(7),本文引入孔板流量系数Cd的概念,认为关于细长限流孔板阻力的计算公式应具有如下形式

(11)

由式(11)可以看出,Cd越大,孔板阻力越小。根据本文实验结果可知:孔板阻力随孔板长度的增大而增大,随孔板直径的增大而减小。因此,流量系数与L/d呈负相关。随着Re的增大,Cd先增大然后趋于一个定值[9],因此流量系数可以表示为

(12)

式中:α、β、m、n为常数,与L/d及Re的范围有关。对本文实验数据进行非线性回归,得到

(13)

图7给出了本文关联式的预测值与实验值的对比结果。由图可以看出,本文关联式的预测误差绝大多数都落到了±15%误差带内,计算得到εMAD、εMARD分别为0.3%和7.79%。这表明本文关联式预测精度较高,可以较为准确地预测孔板长径比为5～70、孔内雷诺数为1.5×105～3.0×106时孔板的阻力特性。