锂电池组高温节点空气冷却方案的数值模拟

2018-07-25路昭余小玲张立玉韦立川高松邱亚林金立文孟祥兆

西安交通大学学报 2018年7期

路昭, 余小玲, 张立玉, 韦立川,3, 高松,4, 邱亚林, 金立文, 孟祥兆

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.西安交通大学人居环境与建筑工程学院, 710049, 西安;3.深圳市英维克科技股份有限公司, 518000, 广东深圳; 4.中国工程物理研究院材料研究所, 621907, 四川江油;5.云南电力试验研究院, 650051, 昆明)

锂离子电池因能量密度高、循环寿命长、自放电率低、工作温度范围宽等优点受到了行业的青睐,是目前纯电动汽车首选的动力蓄电池[1-2]。作为纯电动汽车唯一的动力源,动力锂离子电池的工作性能直接影响电动汽车的安全、高效运行。影响电池性能的因素主要包括电池材料、结构设计及运行温度等。对于商业用锂离子电池而言,目前常关注的是锂离子电池的运行温度对电池性能的影响。由于熵变、欧姆内阻及极化内阻的影响,锂离子电池在充放电过程中均会产生大量的热量,特别是对于密集布置的动力电池组而言,电池包内部单体电池产生的热量互相影响、迅速聚集,会导致动力电池组温度急剧升高。当电池温度过高时,不仅会加速电池老化、缩短电池使用寿命,严重时还会导致电池发生热失控,进而造成难以估计的安全事故[3-5]。此外,学者们还研究了动力电池组内部温度均匀性对锂电池性能的影响,结果表明不均匀的温度分布会造成动力电池组内部各电池单体不一致的充放电特性,从而导致电池组能量利用不充分及性能衰减[6-7]。根据以上分析,为确保电动汽车安全、高效运行,动力电池组需要在适宜的温度范围工作。目前普遍认可的锂离子电池最佳工作温度范围为25～40 ℃[8],因此电池热管理系统已经成为电动汽车动力电池组安全、高效运行的必要组成部分。

目前,各种形式的电池热管理系统都得到了广泛的研究和应用,如空气热管理系统、液体热管理系统及相变储能热管理系统[3,6-7,9-11]。由于结构简单、制造成本低、自消耗能量少等优势,传统的空气热管理系统目前仍然是大多数电动汽车厂家的首选方案。需要强调的是,精心设计的空气热管理系统依然能够满足绝大多数电动汽车动力电池组的运行温度要求[9-11]。Mahamud等通过建立二维数学模型,研究了往复式空气流对顺排布置动力电池组温度特性的影响规律,结果表明往复式空气流冷却方案可以有效降低动力电池组的最高温度和最大温差[9]。Wang等采用ANSYS Icepak 14.5商业软件建立了三维数学模型,用来研究空气冷却方案和电池布置方式对动力电池组热特性的影响[10]。研究者普遍认为,最佳的空气冷却方案应该同时考虑冷却效果、电池组空间利用以及经济性。本文作者前期对冷却空气纵掠密集布置动力电池组进行了相关研究,发现强迫空气冷却能够有效改善动力电池组内部的温度分布,并且通过综合考虑冷却效果和电池组空间利用,获得了合适的电池间距[11]。

根据以上文献可知,目前对电动汽车动力电池组空气热管理系统已经进行了大量的研究,并且针对影响动力电池组温度特性的因素,如送风策略、电池组布置方式,提出了相应的优化方案。众所周知,为确保电池正负极与导电片接触良好、固定可靠,用单体电池组成动力电池组往往需要大量的电池正负极固定件。然而,目前关于动力电池组的研究往往忽略了电池正负极固定件的影响,其原因一是研究者们普遍认为电池正负极固定件主要只是起满足电绝缘及固定电池的作用;二是研究者们主要关注电池自身产热及电池与冷却介质之间的换热能力,而忽略了电池正负极固定件的传热性能。基于此,本文建立了含电池正负极固定件的动力电池组三维数学模型,研究了送风速度、固定件热导率对动力电池组温度特性的影响规律,获得了满足电池正负极固定件绝缘性能的最优热导率,并且基于电池正负极固定件最优热导率,采用导热翅片改善了动力电池组内部的温度均匀性。

1 物理模型

图1为动力电池组错列布置示意图,该动力电池模组主要由Sanyo18650锂离子单体电池和环氧树脂电池正负极固定件组成。单体电池直径D=18 mm,长度L=65 mm,环氧树脂固定件厚度δt=18 mm,电池组纵向节距比Pl/D=1,横向节距比Pt/D=1.1,环氧树脂固定件的中心距Fp=65 mm。

由图1可知,单体电池在x-y平面周期性错列布置并联连接,沿z方向周期性布置串联连接。因此,本文选取2个相邻固定件之间的电池单元进行研究。计算区域、固定件及固定件处的翅片如图2所示。

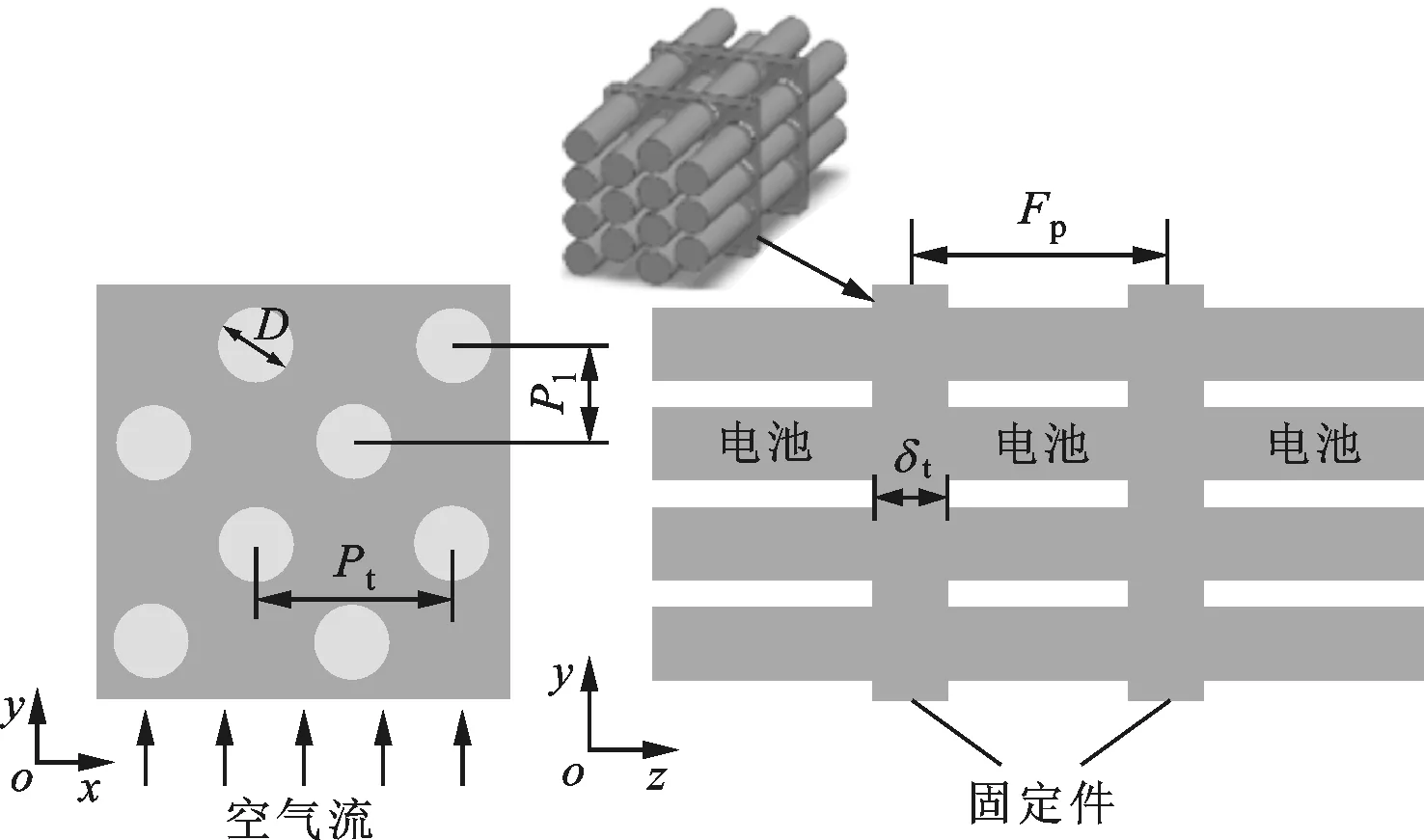
图1 动力电池组错列布置示意图

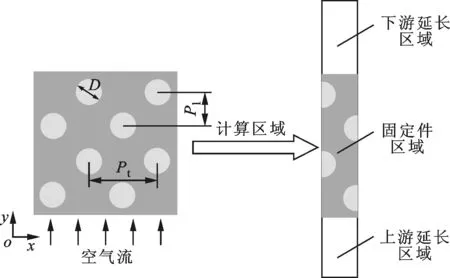
(a)计算区域二维示意图

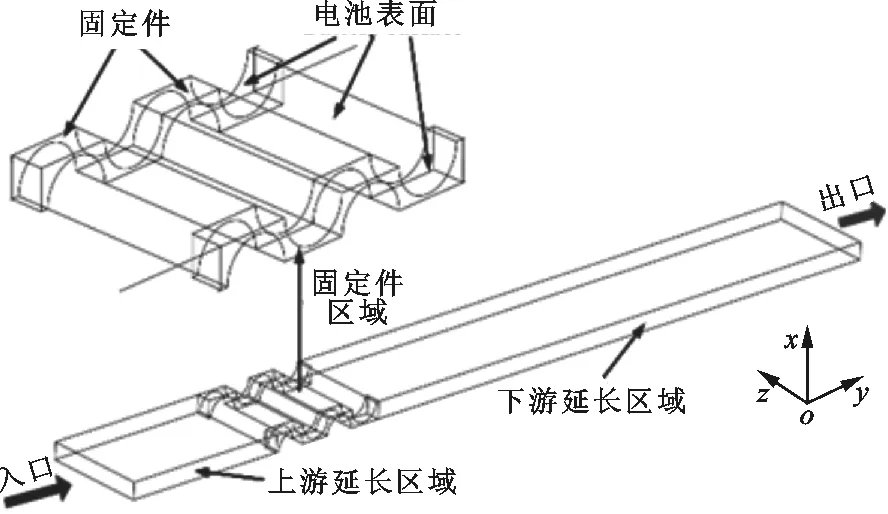
(b)含有固定件的计算区域三维示意图

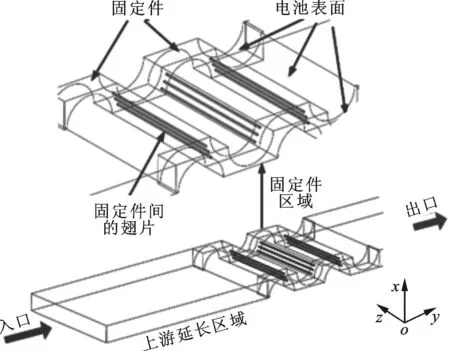
(c)含有翅片的计算区域局部示意图图2 系统计算区域及含固定件和固定件处翅片的计算区域示意图

为减小固定件厚度对计算区域入口空气速度分布的影响,将计算区域入口延长1.5倍,同时为确保冷却空气单向均匀流出计算区域,将计算区域出口延长5倍,此方法已经被广泛应用于翅片管换热器的相关研究[12-13]。因此,整个计算区域沿流动方向的长度是实际固定件区域长度的7.5倍。为进一步改善固定件的散热情况,在相邻2个固定件之间布置一定数量的导热翅片,导热翅片尺寸为0.5 mm(x)×0.5 mm(y)×47 mm(z)。

2 数学模型

2.1 控制方程及基本假设

尽管电池瞬态产热模型能够准确地预测电池的瞬时产热量,但是瞬态产热模型往往需要消耗大量的计算时间。同时,考虑到电池正负极固定件对动力电池组散热性能的影响,空气横掠动力电池组内部的换热问题不仅包括冷却空气与电池表面、固定件表面及翅片表面的强迫对流换热,还包括固定件及翅片内部的导热,因此对于动力电池组而言,这种复杂的瞬态耦合换热问题在求解时间上缺乏可行性。本文的目的是揭示电池正负极固定件对动力电池组换热与流动性能的影响规律,因此,采用平均面热源模拟电池发热量以减少数值计算时间,这种简化方法目前常用于动力电池组的热管理研究[11,14]。

考虑到动力电池组内部空气流速较小,温度变化不大,因此假定冷却空气为不可压缩流体、常物性、层流流动。此外,由于实际应用中常采用导热性能优良的导热硅胶填充于固定件与电池表面之间狭小的缝隙处以确保两者紧密接触,减小接触热阻对动力电池组内部热环境的影响,因此本文忽略了固定件与电池表面之间的接触热阻。采用商业软件ANSYS14.5研究空气横掠错列布置电池组内部的流动与换热问题,描述计算区域内部冷却空气换热与流动问题的控制方程主要包括:

连续性方程

(1)

动量方程

(2)

能量方程

(3)

当流体速度为零时,固定件及翅片区域的能量方程可简化为

(4)

以上各式中:u为流体速度,m·s-1;ρ为密度,kg·m-3;μ为动力黏度,Pa·s;cp为比定压热容,J·kg-1·K-1;λ为热导率,W·m-1·K-1;j为笛卡尔坐标。

2.2 边界条件

冷却空气进口采用速度入口边界条件,并假设同一送风口的所有位置送风速度和送风温度为相同的值;出口采用自由流出边界条件,即所有的空气都单向均匀流出;电池表面采用恒定热流密度边界条件,q=24.4 W·m-2,该值通过电池平均发热量与电池有效传热面积之比求得;固定件与电池和冷却空气的接触面均为耦合边界条件。

2.3 数值方法

首先采用前处理软件Gambit 2.4.6建立动力电池组的物理模型,然后用结构化网格(四边形和六面体网格)对空间进行网格划分,并在电池表面、翅片表面、送回风口附近采用适当的网格加密。经过网格数独立性测试验证,数值计算时选取的网格数为723 190。采用二阶迎风格式对控制方程进行离散化,并选用SIMPLE算法对离散方程进行求解。

3 结果与讨论

3.1 模型验证

目前尚未见到研究电池正负极固定件对动力电池组散热性能的影响的相关报道,无法直接用前人的相关数据来验证本文所建立的数学模型,所以采用文献[15]中的方法,即采用冷却空气横掠翅片管的相关数据进行验证。数学模型验证的相关参数如下:管外径为18 mm,管壁温度为37.7 ℃,管束入口冷却空气温度为16 ℃,入口空气流速变化范围为0.67～4 m·s-1。一般而言,空气横掠翅片管束的流动可看成包括2种流动:一种是空气在相邻2个翅片间的管内流动,此时翅片管束内空气的雷诺数变化范围为333～2 000(<2 300),属于层流流动;另一种是空气横掠管束的流动,此时翅片管束内空气的雷诺数变化范围为1 000～6 000,也属于层流流动(<1.4×105)。因此,在数学模型验证时采用层流模型进行研究。图3给出了努塞尔数随雷诺数的变化规律,可以发现本文数学模型的计算结果与文献[12]的实验结果相近,最大偏差小于5%,由此说明,本文所建立的数学模型和数值方法可用于研究电池正负极固定件对动力电池组热特性与流动特性的影响规律。

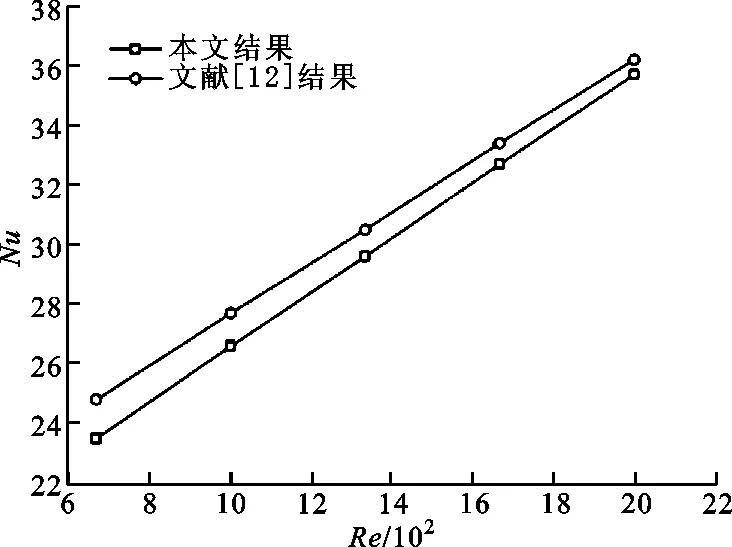
图3 努塞尔数随雷诺数的变化规律

3.2 电池正负极固定件的影响

为了揭示电池正负极固定件对动力电池组内部温度的影响,首先研究了无固定件时动力电池组内部的温度情况,将其称为算例1;其次研究了绝缘性能优良、导热性能较差的环氧树脂作为传统电池正负极固定件对动力电池组内部温度的影响,将其称为算例2;最后根据上述研究结果,研究了不同固定件的热导率对动力电池组内部温度的影响,获得了满足电池正负极固定件绝缘性能的最佳热导率,将其称为算例3。

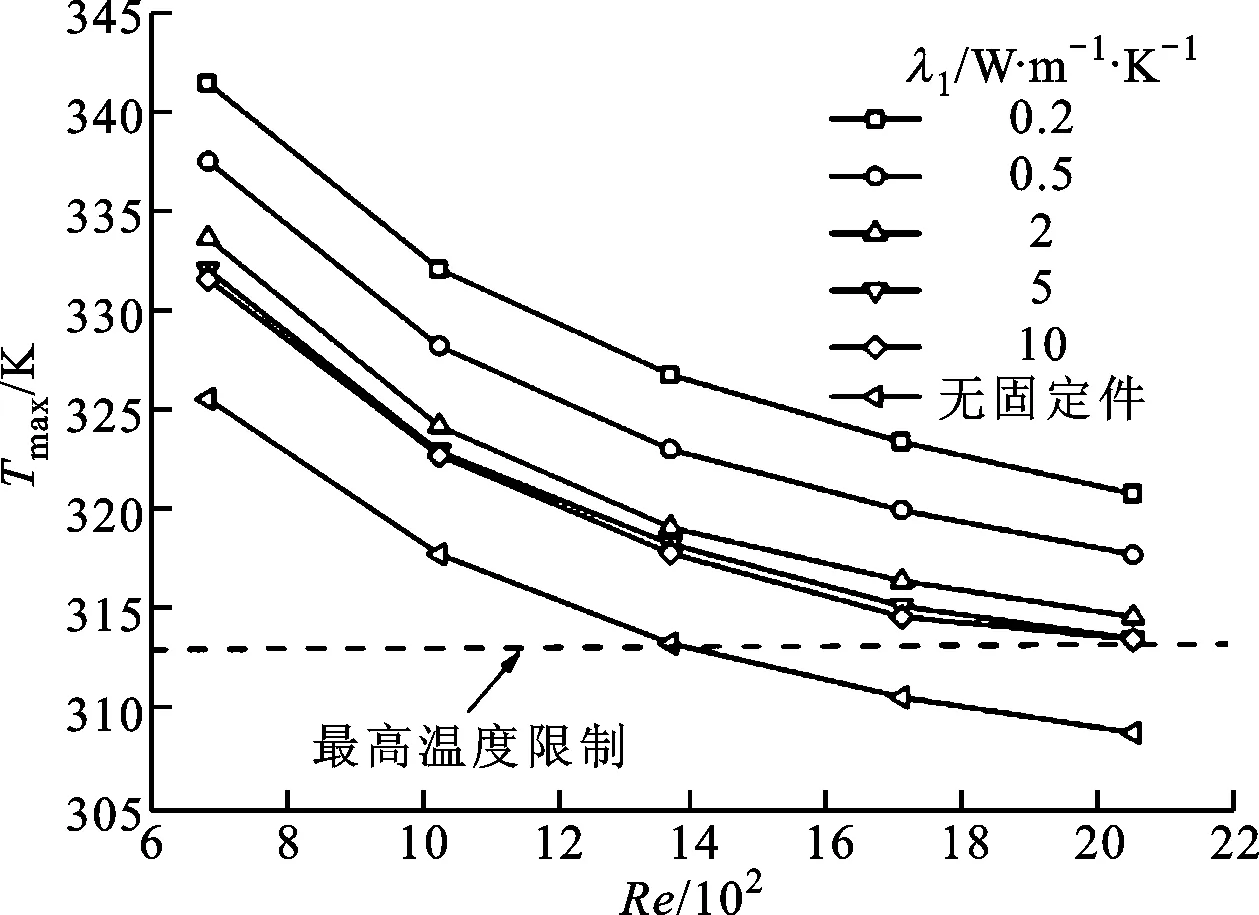
电池正负极固定件对动力电池组内部最高温度的影响如图4所示,从中可以发现,在所研究的雷诺数范围内,未考虑固定件的动力电池组内部最高温度显著低于传统环氧树脂(λ1=0.2 W·m-1·K-1)作为固定件时的最高温度。例如:当Re=2 052时,前2种算例的动力电池组内部最高温度相差约12 K;当1 3682 W·m-1·K-1时,固定件热导率对动力电池组内部最高温度的影响显著减小,说明当冷却空气在错列布置的动力电池组内部处于层流流动时,可使动力电池组整体的散热性能达到最优的固定件热导率为2 W·m-1·K-1,这主要是因为当固定件热导率大于2 W·m-1·K-1时,导热热阻在总传热热阻中的比重显著减小,即固定件热导率对动力电池组整体散热性能的贡献明显降低。此外必须注意的是,固定件首先必须确保动力电池组的电绝缘性能,其次才是满足动力电池组的散热需求。目前,环氧树脂基氧化铝复合材料因兼具优良的绝缘性能和较好的导热性能而得到了普遍关注,常用于绝缘、散热性能要求较高的电子产品冷却中。经文献调研得知,当热导率为2 W·m-1·K-1时,环氧树脂基氧化铝复合材料具有优良的绝缘性能[16],由此说明本文在一定的雷诺数范围内所得到的动力电池组正负极固定件的最优热导率(2 W·m-1·K-1)具有实际工程意义。

图4 固定件热导率对动力电池组最高温度的影响

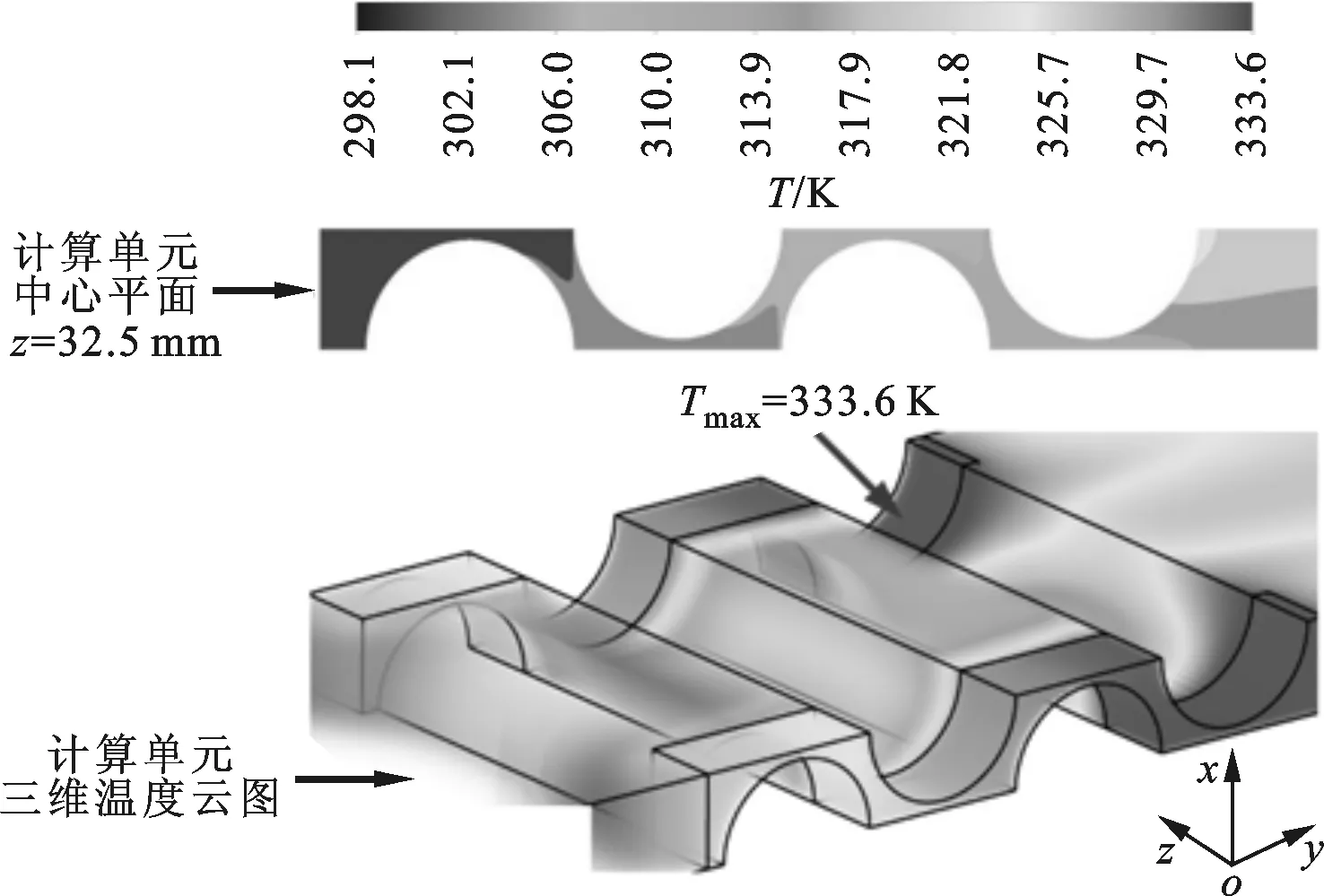
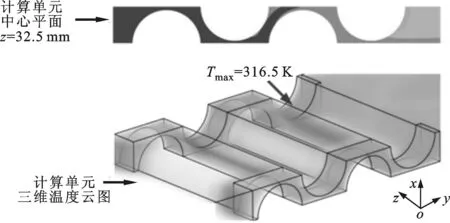
图5为动力电池组在最优热导率、不同雷诺数下的温度云图。从计算单元的三维温度云图可知,动力电池组的高温区域均出现在沿冷却空气流动方向下游侧的固定件处,固定件之间的区域温度明显较低。此外,从计算单元中心截面z=32.5 mm处的温度云图可知,与冷却空气直接接触的电池表面的最高温度明显低于动力电池组的最高温度。例如,当Re=2 052时,动力电池组的最高温度约为314.7 K,而与冷却空气直接接触的电池表面的最高温度约为308.5 K,两者相差6.2 K。上述结果主要由以下3个原因所导致:一是虽然采用了具有最佳热导率的固定件,但是由于其自身导热热阻的影响,依然增大了固定件处电池表面与冷却空气的传热热阻;二是固定件之间的电池表面与冷却空气间仅存在对流传热热阻;三是冷却空气沿流动方向不断带走动力电池组产生的热量,因此空气流温度逐渐升高,导致下游侧空气换热能力下降。

由图5e可以看出,当Re=2 052时,采用最优热导率的动力电池组内部最高温度为314.7 K,最大温差ΔTmax=14.9 K,均超过了动力锂离子电池组的最高温度限制(313.15 K)和最大温差限制(10 K)。因此,为了确保动力锂离子电池组在适宜的温度范围内运行,需要进一步强化动力电池组的空气冷却能力。

3.3 电池正负极固定件处翅片的影响

(a)Re=684

(b)Re=1 026

(c)Re=1 368

(d)Re=1 710

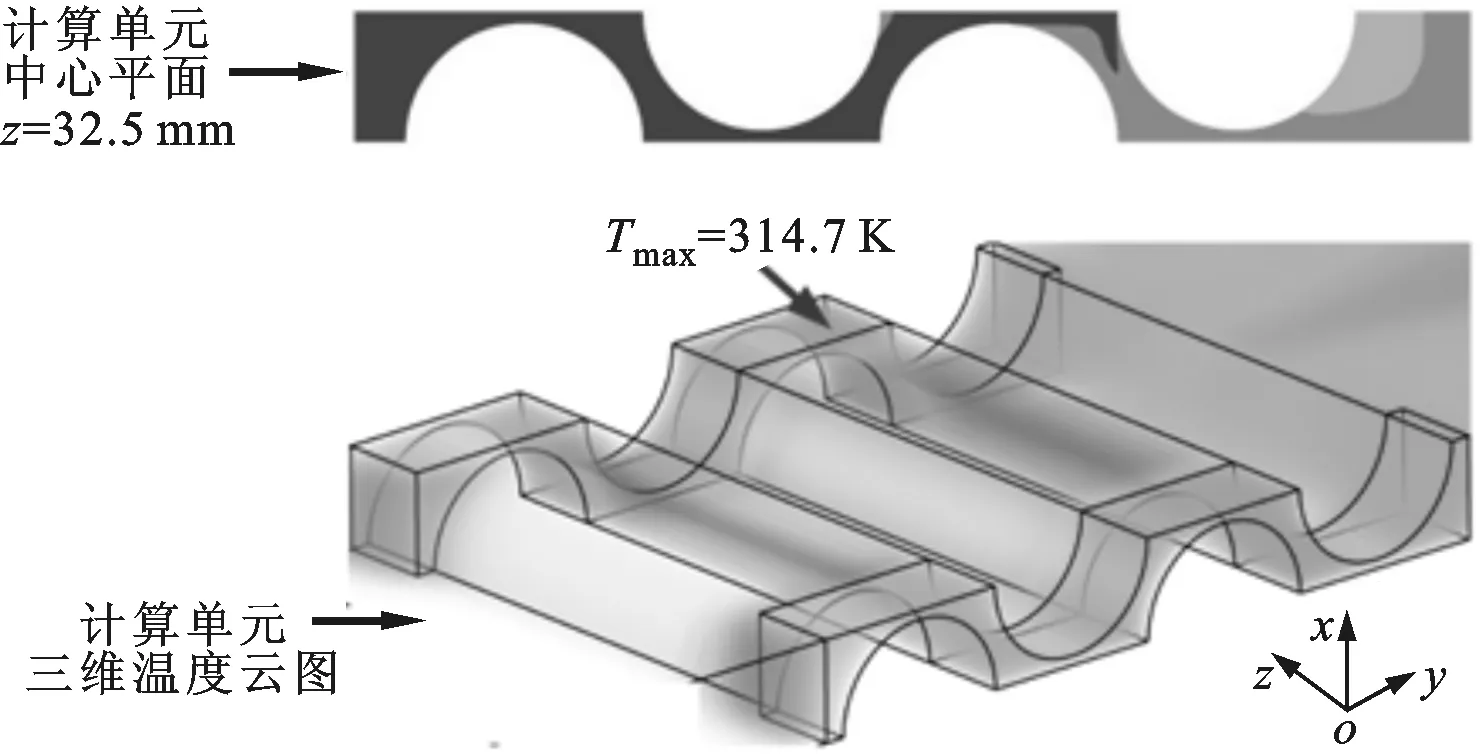
(e)Re=2 052图5 不同雷诺数下动力电池组计算单元的温度云图(λ1=2 W·m-1·K-1)

由3.2节可知,采用最优热导率的动力电池组具有优良的散热性能,然而在所研究的雷诺数范围内,动力电池组内部的热环境依然不能满足锂离子电池的温度要求。根据牛顿冷却公式可知,当电池产热量、冷却空气送风温度一定时,减小冷却空气与电池表面之间的传热热阻可以有效减小电池表面与冷却空气之间的传热温差,即可以降低动力电池组的整体温度。为此,在相连的2个固定件之间布置成组的导热翅片,以减小冷却空气与固定件之间的传热热阻。同时,为了研究导热翅片数量、位置、热导率对动力电池组内部温度的影响,采用2种方案在固定件之间布置导热翅片:方案一是沿冷却空气流动方向在相邻2个电池单元之间均匀布置3个导热翅片,由于本文研究的动力电池组计算单元沿流动方向由4排电池单元组成,因此方案一沿冷却空气流动方向均匀布置9个导热翅片,如图2c所示;方案二是沿冷却空气流动方向在最后2排电池之间布置3个导热翅片。

图6给出了冷却空气雷诺数为2 052、固定件为最优热导率(2 W·m-1·K-1)时,动力电池组内部最高温度随导热翅片热导率的变化规律。

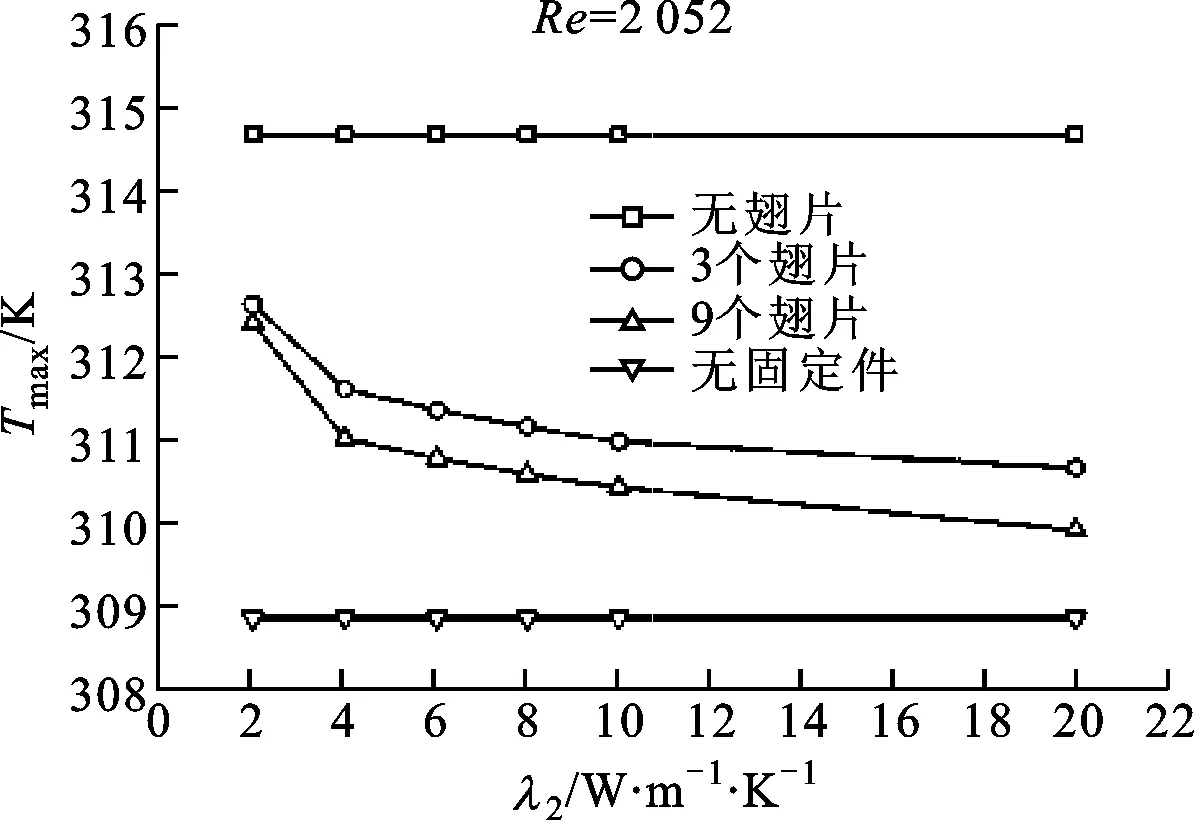
图6 导热翅片热导率对最高温度的影响

图6中最上面的直线为固定件之间没有布置导热翅片时动力电池组的最高温度,将其称为无翅片算例;最下面的直线为无固定件时动力电池组的最高温度,将其称为无固定件算例。在这2个算例中,动力电池组内部最高温度与导热翅片热导率无关,以下将其与增加导热翅片后的算例进行对比。由图6可知,当导热翅片与固定件的热导率均为2 W·m-1·K-1时,无论采用方案一或者方案二,动力电池组内部的最高温度均明显低于无翅片算例动力电池组内部的最高温度,相差约2 K。此外,随着导热翅片热导率逐渐增加,方案一的冷却效果稍优于方案二的冷却效果,2种方案的动力电池组内部最高温度相差约0.7 K。值得注意的是,2种方案的动力电池组内部最高温度的下降幅度均逐渐减小。例如对于方案一而言,当导热翅片的热导率从2 W·m-1·K-1增加到4 W·m-1·K-1时,动力电池组内部的最高温度下降约1.5 K,而当导热翅片的热导率从4 W·m-1·K-1增加到20 W·m-1·K-1时,动力电池组内部的最高温度下降约1 K,主要原因是随着导热翅片热导率的逐渐增大,导热热阻在总传热热阻中的比重逐渐减小,而对流传热热阻的比重逐渐增加,因此导热翅片的热导率对动力电池组整体散热性能的贡献逐渐减小。

冷却空气流过动力电池组需要消耗的风机能量由下式计算

P=pdQV

(5)

式中:pd为冷却空气的进出口压降,Pa;QV为冷却空气的体积流量,m3·s-1。

图7为不同雷诺数下电池正负极固定件、导热翅片数量对冷却空气流过动力电池组需要消耗的风机能量的影响,从中可以看出,随着雷诺数逐渐增大,考虑固定件及导热翅片的风机能耗明显高于无固定件算例的风机能耗。例如,当Re=2 052时,方案一的风机能耗是无固定件算例风机能耗的1.8倍。此外,方案一和方案二的风机能耗与无翅片算例的风机能耗差异不大。特别是在所研究的整个雷诺数范围内,方案二的风机能耗与无翅片算例的风机能耗基本相同。

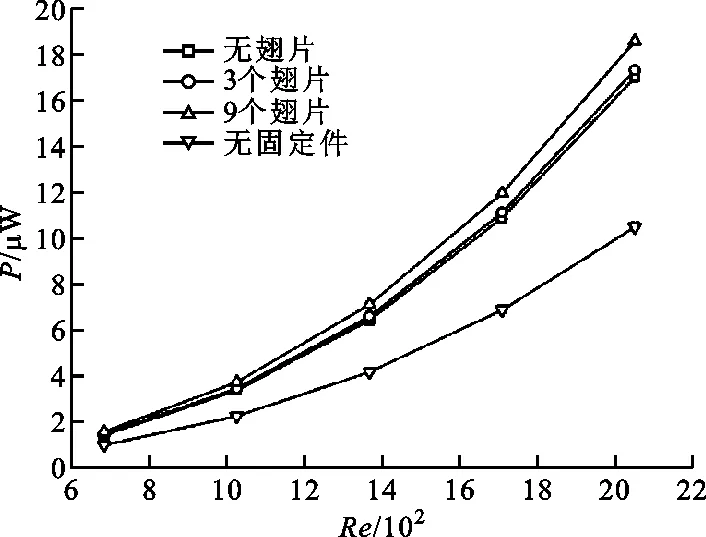
图7 不同雷诺数下固定件、翅片数量对风机能耗的影响

综上所述,固定件之间布置导热翅片可以显著提高动力电池组的整体散热性能,确保动力电池组内部最高温度低于锂离子电池的最高温度限制(313.15 K)。此外,动力电池组能否高效运行也与动力电池组内部温度的均匀性密切相关。因此,为了进一步获得导热翅片对动力电池内部温度均匀性的影响,计算出了冷却空气雷诺数为2 052、导热翅片热导率为20 W·m-1·K-1时动力电池组的温度云图,如图8所示。

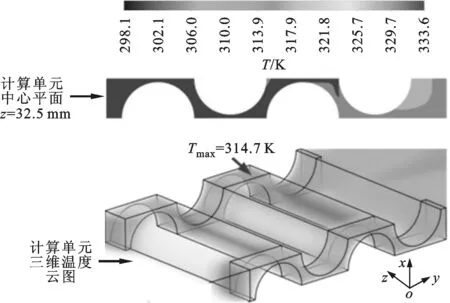
(a)无翅片算例

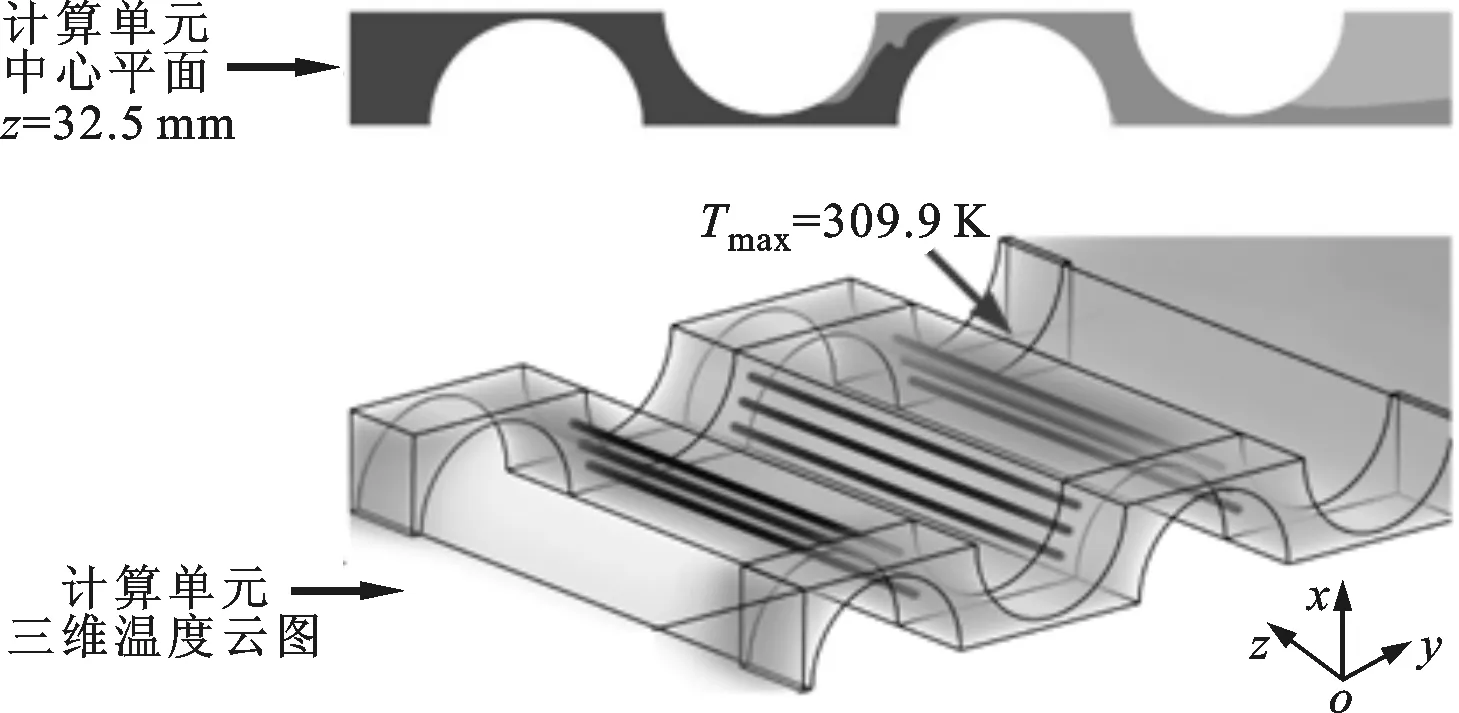
(b)方案一

(c)方案二图8 动力电池组的温度云图(Re=2 052,固定件热导率λ1=2 W·m-1·K-1,翅片热导率λ2=20 W·m-1·K-1)

由图8可以看出:相对无翅片算例而言,方案一和方案二的动力电池组内部温度分布均匀,固定件处并没有出现明显的高温区域。此外,方案一和方案二的动力电池组内部最大温差分别为9.6 K和10.5 K,明显低于无翅片算例的动力电池组内部最大温差14.9 K。上述结果表明,固定件处增加导热翅片能有效强化动力电池组内部的空气换热能力,使得高温区域的温度显著降低,从而减小了动力电池组内部各单体电池之间的温度差,有利于各单体电池实现一致的充放电特性,确保动力电池组安全、高效运行。