物理教学中数学能力培养探讨
2018-07-25湖北
湖北
朱木清
应用数学处理物理问题的能力,既是物理教学需要,也是高考的重要要求,体现国家未来科技和人才战略思想,高校与中学、教师和学生都应有足够的认识和相应的作为。而现实的种种局限,也有物理学科本身难学因素影响,使相当一部分学生缺乏数理融合意义和训练感悟,导致物理学得很吃力。
作为物理教师,我们不能放松、更不能放弃“应用数学处理物理问题的能力”的教学要求,必须审慎当下困难,寻求措施办法,奋力促进数理融合。这里,以个人的教学实践,谈点肤浅的体会和建议,供大家参考。
1.打通“断头路”, 补齐短板,增强数理融合的主动意识
物理中的数学能力培养,在大学有数学物理方法课程,在中学还是自由生长。面对当下窘境,物理教师需对各阶段教学所需数学工具作以盘点,并与本校数学教师沟通,拟定一个数学补习实施方案,下达指导学生定出针对自身的行动计划,这样多方配合联动,减少劳动浪费。
1.1.适时补习高一物理学习必需的数学知识
初中到高中,物理由具体到抽象,定性到定量,将用到大量数学知识。然而,由于现行教材数理两科缺乏协同,数学滞后物理很多,给高一物理学习带来很大困难,严重制约新课教学。问题缘起虽在课程顶层设计,而当前的教学困难又不能回避。基于初中数学缺陷,为解燃眉之急,需适时进行必要的数学补充。
实践表明,在高一物理必修1的第一、二、三章相关部分前,穿插补充相关数学内容:矢量与标量、三角函数部分内容及解析几何中方程与图线基础,对学生学习很有帮助。物理教师需打破“学科本位”,“客串”数学,亲自动手编拟简明实用的校本教材。例如可在第一章前穿插函数与图线基础,第二章前穿插锐角三角函数和解斜三角形,解决急需问题。要利用网络平台,督促学生配合行动。教学中,尤其是起步阶段,遇到与数学关联的重要节点,注意放慢速度讲细点,密切两科联系,夯实基础。
【例1】某物体沿x轴运动,其速度与时间的关系如图1所示,则下列说法正确的有 ( )

A.物体的加速度a=0.75 m/s2
B.物体的速度变化率为0.5 m/s2
C.t=4 s时物体所在位置坐标x=4 m
D.0~1 s内物体的位移为4 m
【答案】BD

本例涉及数学与物理几个相关基础概念,如果数理两科教师都无视其关联作用,就可能给学生留下知识盲区,受伤的是物理。但现实又缺乏这类纠错题,故只有物理教师亲自动手现编,自产自销,填补空白。

1.2领会教材编写意图,认识数学物理方法的地位和作用
物理学是应用数学思想与方法最充分、最成功的一门科学。高中物理课程标准中明确指出,高中的物理教学应该通过物理概念和规律的学习过程,使学生了解物理学的研究方法,认识物理实验、物理模型和数学工具在物理发展过程中的作用。要求教师在教学中注重物理思想、方法渗透过程的同时,也应充分体现数学工具对物理学发展所起的促进作用。这一思想编织贯穿到教材中。
高一开篇“直线运动”,教材穿插补充了一些数学知识,如增加运动图象的篇幅,小专题介绍变化率概念,利用速度图象“面积”推导匀变速直线运动位移,渗透微积分思想。所有这些,反映出教材编写的深刻用意:物理离不开数学。物理和数学,就像图和数的关系,形影难离。 数离开图不直观,图离开数不具体。可以这样说,离开了数学思想与方法,就没有真正意义上的物理学。
【例2】意大利物理学家伽利略对自由落体运动的研究,开创了科学实验和逻辑推理相结合的重要科学研究方法。如图2所示,他先观测小球分别沿倾角不同、阻力很小的斜面从静止开始运动的情况,再进行逻辑推理。关于本实验下列说法正确的有 ( )

A.利用倾角较小的斜面进行实验,可“冲淡”重力,使时间测量相对容易
B.通过外推证实自由落体运动也是匀加速直线运动
C.斜面上小球运动速度的变化对位移是均匀的,即速度与位移成正比
D.斜面上小球运动速度的变化对时间是均匀的,即速度与时间成正比
【答案】ABD
在伽利略时代,不能通过实验直接测定瞬时速度来验证一个物体是否做匀变速运动。伽利略结合实验,应用数学和逻辑推理方法得出:初速度为零的匀加速运动物体发生的位移与所用时间的平方成正比,并外推到自由落体运动也是匀加速运动。300多年过去了,伽利略发现的自由落体运动规律,在整个物理学中不过是沧海一粟,地位影响愈来愈低,但他创造的抽象思维、数学推导和科学实验相结合的研究方法,为人类走出千年科学研究泥潭,开启近代科学大门,贡献了最珍贵的思想智慧。对于伽利略的成就和获得成就的方法,爱因斯坦赞扬最具有代表性:“伽利略的发现以及他所应用的科学的推理方法,是人类思想史上最伟大的成就之一,而且标志着物理学的真正开端”。高中物理必修1增加的这节内容,是数学物理思想方法的最光辉典范。伟人创造的科学思维方法,后人受用,是必须吸收和传承的精神财富。
2.注重基础,明确要领,着力掌握物理模型向数学模型转化的技能
数理两科相伴而生,研究方法一脉相通。但在很多同学心底,却把它们划得很开。不少同学,学了不少数学知识,并能解决一些较复杂的数学问题,但遇到物理中有些与数学相关的基本问题,却理解不了;遇到一些需用数学处理的物理问题,常是思维混乱,甚至无从下手。因此,了解一些数学用于物理的基本常识,知道物理研究的基本方法和思维程序,是促进数理融合不可或缺的前提条件。
2.1知道数理描述的联系和区别
【例3】物理关系式中比例系数的确定。

2.2明确解决物理问题的一般思维程序,知道数理模型转化的方法要领
物理问题的求解一般要经过下图所示几个基本环节:

(1)实际问题向物理模型的转化环节
这一步是审题分析的反映,是物理解题的基础和前提。所谓物理模型,就是按照由简到繁,由易到难,循序渐进,逐层深入的原则,依据问题性质,忽略次要因素,抓住主要矛盾,突出本质特征,构建出的理想化研究对象,是研究复杂问题的科学方法策略。物理模型包括实体模型,状态模型,过程模型,如质点、点电荷、匀强电场、理想电表、理想流体、静态平衡、动态平衡、临界状态、匀变速运动、匀速圆周运动等。
(2)物理模型向数学模型的转化环节
这一步是实现物理解题的重点和关键。所谓数学模型,就是利用数学的概念、方法和理论,借助符号、字母、图形和数字等数学语言描述研究对象,反映问题中各要素之间关系的数学形式。简言之, 就是把实际问题翻译成纯数学语言。具体的数学模型,分布在函数与方程、不等式、平面三角与解析几何、复数与向量、数列与数学归纳法、极限与微积分等各部分。
数学应用于物理,落脚到解题,就是分析物理模型的相关量,哪些是常量,哪些是变量;哪些是矢量,哪些是标量;哪些是过程量,哪些是状态量;哪些是已知量,哪些是待求量。再根据物理规律找出各物理量之间的关系式。
(3)数学模型的求解环节
这一步需要数学技能的支撑,对解题者掌握的数学工具提出要求。
(4)数学模型解还原到物理模型解的环节
这一步需特别注意物理模型的适用条件和范围,防范物理问题数学化错误,作出必要检验和讨论。
【例4】物理模型与数学模型的区别。

3.加强训练指导,久久为功,让数学方法在物理应用中有获得感
应用数学处理物理问题的能力,用高考考试大纲中的语言描述,就是能够根据具体问题列出物理量之间的关系式,进行推导和求解,并根据结果得出物理结论;能运用几何图形、函数图象进行表达、分析。关键在将物理模型转化为数学模型,注意结合物理模型的适用条件范围,给出物理模型解。其间,涉及很多数学工具运用,体现数学的技能技巧。
技能需要反复刻苦训练才能形成,罗马不是一日建成的。高中三年,须从高一做起,数学跟物理结伴同行,坚持一题多解,一题多变,多题一解,总结方法,整理归类,逐步融合加深,力争常见的数学模型逐一到位,定会收获数理双赢,受益终生。
【例5】甲、乙两车在相邻两车道上同向直线运动,同时通过某路标。甲车速度v甲=16 m/s,并开始刹车做加速度大小a甲=2 m/s2的匀减速运动;乙车速度v乙=4 m/s,做加速度大小a乙=1 m/s2的匀加速运动,求:
(1)甲车超前乙车过程中,沿车行方向两车间的最大距离;
(2)t=10 s时刻沿车行方向两车间的距离。
【分析与解答】本题物理模型很明确:两车可视质点,做匀变速直线运动。
第(1)问是极值问题,有多种解法。
方法一:利用函数解析与二次函数模型
两车同时同地同向出发,取路标处为坐标原点,在同一坐标系中:
沿车行方向两车间距离为
s是关于时间t的二次函数,利用二次函数y=ax2+bx+c性质特征或配方法:



故t=4 s时刻,两车间距离最大sm=24 m。
方法二:利用数学图象模型
甲车做匀减速运动,速度vt甲=v甲-a甲t,乙车做匀加速运动,vt乙=v乙-a乙t,作出两车的速度图象,如图3所示。

速度图线与时间轴所夹“面积”表示各自的位移,在t=0~4 s内,甲的位移大于乙,甲超前于乙。两车速度图线的“夹面积”(图中阴影部分)表示相对位移,t=4 s时刻,甲超前乙的距离达到最大值,即
方法三:利用相对运动和矢量运算模型
以乙车为参考系,甲车相对于乙车,初速度u0=v甲-v乙=(16-4) m/s=12 m/s,加速度大小a′=a甲-(-a乙)=3 m/s2(注意这里矢量计算容易出错),a′的方向跟u0相反,故甲车相对乙车做类似横向的“竖直上抛运动”,满足
ut=u0-a′t


方法四:利用函数解析与导函数等于零模型
如前所述,沿车行方向两车间距离为
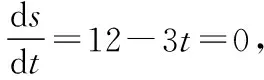
则两车间距离最大值为sm=24 m。
由第(1)问求解可见,解物理极值题方法有:
Ⅰ.物理方法——先找到“取得极值的特征条件”,故亦称条件极值法。如上述方法二中速度相等时取得极值,方法三中是相对速度u=0。
Ⅱ.数学方法——先依据物理模型,把物理问题转化为数学模型,再利用数学方法求极值,如本题方法一和方法四。数学方法求极值时,涉及的数学工具通常有导数、二次三项式配方或判别式、三角函数式的化简与变形、重要不等式性质等;有时也可通过图象分析或“数形结合”求极值,如方法二。
同一物理极值题,物理方法和数学方法通常都可,但有些情况只能用数学方法。物理方法相对简明省时,但要求对过程图景和特征条件理解透彻;数学方法相对耗时,但能带动数学知识和技能复习。

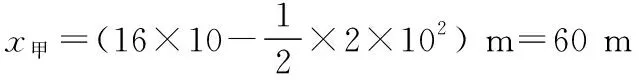


但所求出的两车间距离Δx=x乙-x甲=30 m是错的。问题在什么地方?