用动力学规律解决“滑块—木板模型”问题
2018-07-25广东
广东
古焕标
“滑块—木板模型”问题是高中物理常见的题型,属于多物体多过程问题;此类问题常涉及牛顿运动定律、运动学公式、功能关系等知识点,知识综合性较强,对能力要求较高。在命制试题时,命题者常以“滑块—木板模型”为蓝本,进行适度的拓展、变形、重构和创新来命制考题。而此类模型常隐含临界问题,研究对象多,运动过程复杂,因此属于比较难的一类问题。本文针对“滑块—木板模型”问题的特点和命题的多样性进行归类解析,供教学中参考。
1.模型结构
上、下叠放两个物体,并且两物体在摩擦力的相互作用下发生相对滑动,如图1所示。(滑块B大小可忽略)
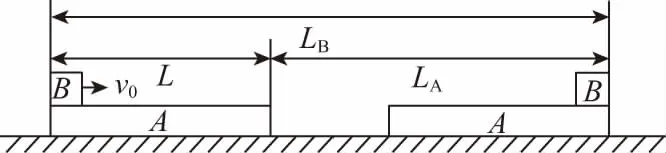
图1
2.模型特点
“滑块—木板模型”问题涉及受力和运动情况分析,特别是对摩擦力、相对运动的临界条件分析;考查位移和时间关系的寻求,临界问题和多过程问题的求解。
3.模型解题方法和思路
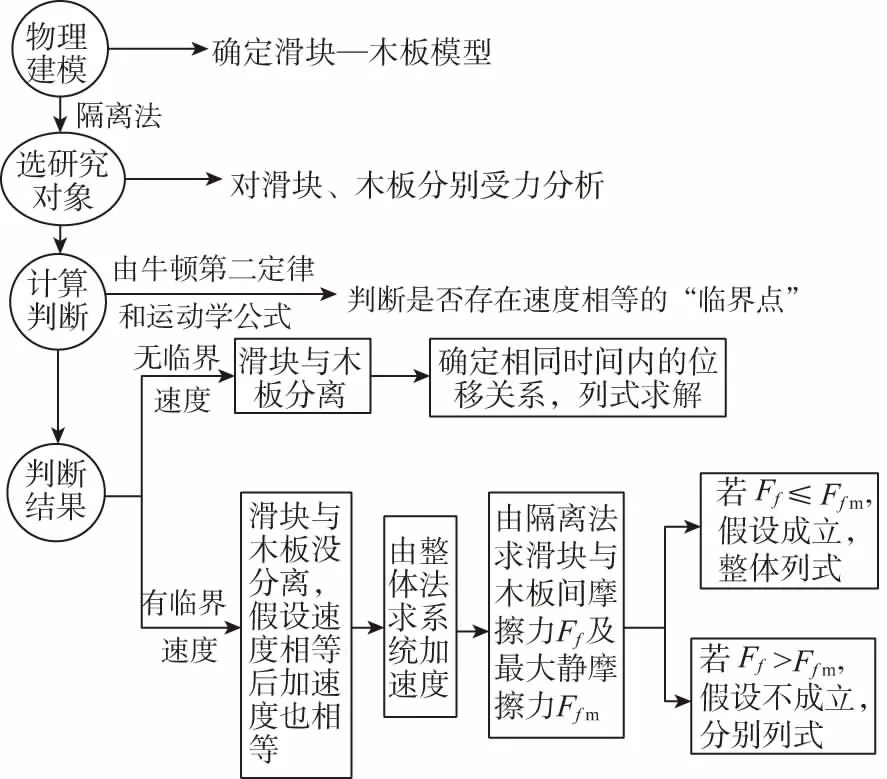
图2
求解这类模型问题可从分析滑块(或木板)的受力和运动情况入手,结合“滑块—木板”的初速度来判定两个物体是否发生相对滑动,求出不受外力F作用的滑块(或木板)的最大临界加速度,并用假设法求出“滑块—木板”在外力F作用下整体的加速度,找出滑块和木板之间的位移关系或速度关系,运用运动学公式、牛顿运动定律等知识来综合求解。其解题的一般思路如图2所示。
4.“滑块—木板模型”的实例分析4.1 滑块以初速度v0运动
【例1】如图3所示,物块A、木板B的质量均为m=10 kg,不计A的大小,B板长L=3 m。开始时A、B均静止。现使A以水平初速度v0从B的最左端开始运动。已知A与B、B与水平面之间的动摩擦因数分别为μ1=0.3和μ2=0.1,g取10 m/s2。若物块A刚好没有从B上滑下来,则A的初速度v0多大?

图3
【解析】分别对物块A、木板B进行受力分析可知,A在B上向右做匀减速运动,加速度大小为a1,则有:
木板B向右做匀加速运动,加速度大小为a2,则有:
由题意可知,A刚好没有从B上滑下来,则A滑到B最右端时和B速度相同,设为v,则有:



【变式】在例1中,若把木板B放在光滑水平面上,让物块A仍以例1中的初速度v0从木板B的最左端开始运动,则物块A能否与木板B脱离?最终物块A和木板B的速度各是多大?

B向右做匀加速运动,加速度大小为a2′,则有:
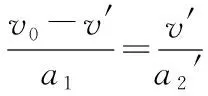




4.2 滑块在外力F作用下运动
【例2】如图4所示,质量M=1 kg的木板A静止在水平地面上,在木板的左端放置一个质量m=1 kg的铁块B(大小可忽略),铁块与木板间的动摩擦因数μ1=0.3,木板长L=1 m,用F=5 N的水平恒力作用在铁块上。设铁块B与木板A间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2。若水平地面光滑,计算说明铁块B与木板A间是否会发生相对滑动。

图4
【解析】设木板A、铁块B之间的最大静摩擦力为Ffm,则有:Ffm=μ1mg=0.3×1×10 N=3 N
假设木板A、铁块B之间不发生相对滑动,对A、B整体进行受力分析,由牛顿第二定律得:F=(M+m)a
对铁块B进行受力分析,设A、B之间的静摩擦力为FfAB,由牛顿第二定律得:FfAB=ma解得:FfAB=2.5 N
因FfAB 【变式】在例2中,若水平地面粗糙,且木板A与水平地面间的动摩擦因数为μ2=0.1,求铁块B运动到木板A右端的时间。 【解析】对铁块B进行受力分析,由牛顿第二定律得: F-μ1mg=maB 对木板A进行受力分析,由牛顿第二定律得: μ1mg-μ2(M+m)g=MaA 设铁块B运动到木板A右端的时间为t,由运动学公式得: A、B之间的位移关系为:xB-xA=L 4.3 “滑块—木板”在倾斜面上的运动 图5 【解析】分别对木板M、小物块m进行受力分析,由牛顿第二定律得: 木板M:F-(M+m)gsinα=(M+m)a 对小物块m:Ff-mgsinα=ma 因Ff≤Ffm=μmgcosα 代入数据得:F≤30 N。 【变式】在例3中,若F=37.5 N,小物块能否滑离木板?若不能,请说明理由;若能,求出小物块滑离木板所用的时间及滑离木板后沿斜面上升的最大距离。 【解析】因F=37.5 N>30 N,所以小物块能滑离木板,由牛顿第二定律得: 木板M:F-μmgcosα-Mgsinα=Ma1 对小物块m:μmgcosα-mgsinα=ma2 设小物块滑离木板所用时间为t,由运动学公式得: 设小物块滑离木板时的速度为v,由运动学公式得: v=a2t 由运动学公式得:0-v2=-2gsinα·x 代入数据得:x=0.9 m。 综上可知,解决“滑块—木板模型”问题的规律方法有: 5.1 分析思路 (1)审题建模:仔细审题,研究题目的含义,分析清楚每一个物体的受力情况、运动情况。 (2)求加速度:准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能发生突变,即临界点问题)。 (3)明确关系:找出物体之间的位移(路程)关系或速度关系是解题的突破口,每一个过程的末速度是下一个过程的初速度。 5.2 分析方法 (1)动力学法:先假设滑块、木板两者相对静止,由牛顿第二定律求出它们之间的摩擦力Ff,与最大静摩擦力Ffm进行比较。若Ff (2)运动学法:①比较滑块与木板的速度和加速度,若相等,则不会发生相对滑动;若不相等,则发生相对滑动。②画出滑块和木板的v-t图象,图象能直观反映两者的运动过程。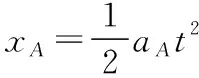





5.方法技巧小结

