质点的直线运动这样教、这样学
2018-07-25山西
山西
石有山
质点的直线运动是高中物理的开篇之作,万事开头难,讲好、学好质点的直线运动尤为关键。本文从最新的考试大纲出发,思考如何教授高中物理的直线运动部分,期待给师生建立一种教和学的模式。
一、考点透视
1.考试大纲:2018考试大纲中,质点的直线运动,共有三个知识点,如下表。

质点的直线运动参考系、质点位移、速度和加速度匀变速直线运动及其公式、图象ⅠⅡⅡ
2.历年全国卷命题实况追踪:
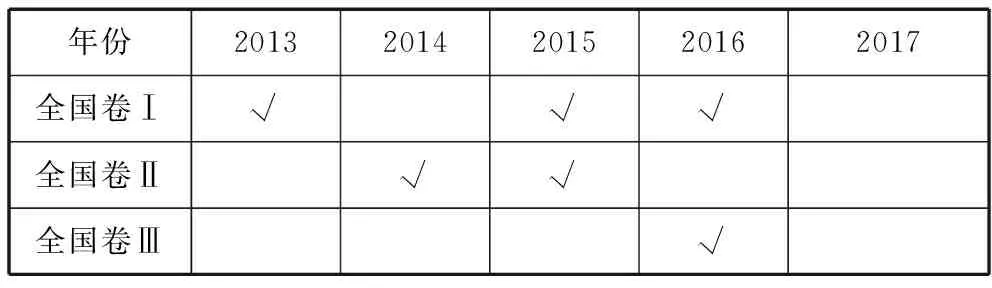
年份20132014201520162017全国卷Ⅰ√√√全国卷Ⅱ√√全国卷Ⅲ√
3.能力要求:通过位移、速度和加速度等基本概念,考查理解能力;通过运动学基本公式和重要推论,考查考生对公式的灵活应用及推理能力;通过实际运动问题,突出考查考生对实际运动的抽象、建模,考查分析和综合能力。
4.命题预测:在近五年高考全国卷的12套试卷中,有6套试卷命制了直线运动试题,但2017年全国卷的三套试卷都没有单独命制的试题,预计该部分内容将是未来几年高考命题的热点,可能是图象问题,可能是追及和相遇问题,也可能是与交通运输、现代科技紧密结合的问题。理解基本概念,掌握运动图象,熟练运用运动学规律,将抽象问题具体化并转化为物理模型是本部分复习的重点。
二、建立物理模型,是解决运动学问题的第一步,是物理学科素养的本质要求
利用物理观念,构建起清晰的物理情景,是科学思维的关键,是学科素养的核心。解题时建立物理模型的过程,就是通过阅读题文和题图,想象物理图景,弄清题目中所涉及的物理过程,明确已知条件与所求问题之间的关系等而进行的分析与综合相结合的思维活动。运动学试题,一般紧密联系实际,试题来源于生活,解题时需要建立起运动模型,根据运动模型和有关运动学知识解题。
【例1】(2016·浙江卷第17题)如图1所示为一种常见的身高体重测量仪。测量仪顶部向下发射波速为v的超声波,超声波经反射后返回,被测量仪接收,测量仪记录发射和接收的时间间隔。质量为M0的测重台置于压力传感器上,传感器输出电压与作用在其上的压力成正比。当测重台没有站人时,测量仪记录的时间间隔为t0,输出电压为U0,某同学站上测重台,测量仪记录的时间间隔为t,输出电压为U,则该同学的身高和质量分别为 ( )

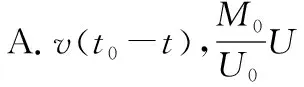
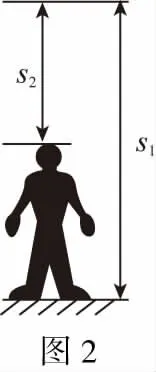
【物理模型】建立起超声波测量模型。人未站上测量仪时,超声波的反射距离如图2中的s1,人站上测量仪时,超声波的反射距离如图2中的s2,故人的身高为h=s1-s2。

【答案】D
【点评】试题来源于我们身边的现实生活。建立起超声波测量模型,即人站上体重计时,超声波反射点减小的高度为人的身高是解决问题的关键。
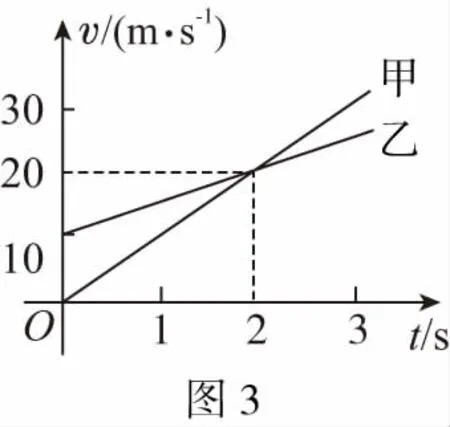
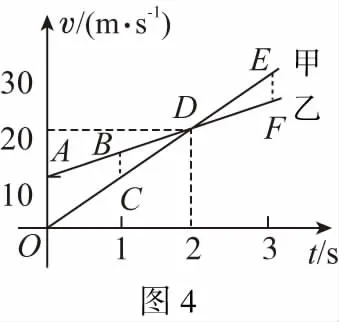
【例2】(2016·全国卷Ⅰ第21题)甲、乙两车在平直公路上同向行驶,其v-t图象如图3所示。已知两车在t=3 s时并排行驶,则 ( )
A.在t=1 s时,甲车在乙车后
B.在t=0时,甲车在乙车前7.5 m
C.两车另一次并排行驶的时刻是t=2 s
D.甲、乙两车两次并排行驶的位置之间沿公路方向的距离为40 m
【物理模型】建立追及和相遇问题模型。本题为匀加速追匀加速,解题的突破口为两车在t=3 s时并排行驶,可得t=1 s两车也并排行驶,由此可得运动模型为两车0时刻的起点不同,初速度不同,甲车初速度为0,加速度大,乙车初速度不为0,加速度小,根据图象可知两车相遇两次。
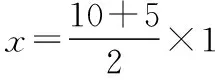
【答案】BD
【点评】追及和相遇问题是一类常见的运动学问题。本题以两车在t=3 s时并排行驶为突破口,从v-t图象建立起运动模型,利用有关运动学知识解决问题。
三、灵活应用方法
灵活应用方法是解决运动学习题的重要技巧,运动学习题,很灵活,巧解运动学习题是教与学的重点。解决运动学习题一般应用解析法和图象法。
1.解析法常用方法:
(1)一般公式法:一般公式法是指利用匀变速直线运动的五个基本公式解题。它们均是矢量式,使用时注意方向性。一般以初速度v0的方向为正方向,其余矢量与正方向相同时为正,与正方向相反时取负。

(3)比例法:对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的比例关系求解问题。
(4)逆向思维法:把运动过程的“末态”作为“初态”的反向研究问题的方法。一般用于末态已知的情况。
(5)巧用推论解题:匀变速直线运动中,连续相等的时间T内的位移之差为一恒量,即Δx=xn+1-xn=aT2,对一般的匀变速直线运动问题,若出现相等的时间间隔,应优先考虑用Δx=aT2求解。
2.图象法:用图象表达运动规律,简明、形象、直观,解题时应用得当,会使问题变得非常简单。运动图象主要为x-t、v-t、a-t等,同时也作为理解其他图象的基础。其中v-t图象提供的信息最多,应用也最广泛,但近几年的考题对其他类型的图象也有涉及。
【例3】(2016·上海卷第14题)物体做匀加速直线运动,相继经过两段距离为16 m的路程,第一段用时4 s,第二段用时2 s,则物体的加速度是 ( )


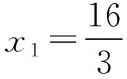
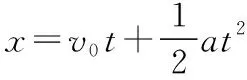
【答案】B
【点评】对于匀变速直线运动中间时刻的瞬时速度等于整段的平均速度,把平均速度转化为瞬时速度,意义重大。
四、教学实例分析
【例4】甲、乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机,需在接力区前适当的位置设置标记。在某次练习中,甲在接力区前s0=13.5 m处作了标记,并以v=9 m/s的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒。已知接力区的长度为L=20 m。求:
(1)此次练习中乙在接棒前的加速度a;
(2)在完成交接棒时乙离接力区末端的距离。
运动模型:帮助学生建立运动情景,画出草图,转化为同时、不同地出发的追及和相遇问题。
运动草图:

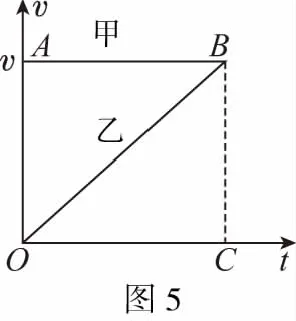
【解法一】根据v-t图象解题。如图5所示,运动员甲做匀速运动,运动员乙做匀加速直线运动,二者速度相等时刚好被追上。根据图象与坐标轴围成的面积表示位移,甲比乙多走的距离为OAB的面积,大小等于s0,因三角形OBC和三角形OAB面积相等,因此乙对地的位移大小也为s0,根据2as0=v2得a=3 m/s2,完成交接棒时乙离接力区末端的距离为Δs=L-s0=6.5 m。
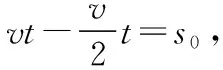
【解法三】用相对运动法解题。以乙为参考系,研究甲的运动情况,则相对位移为s0,相对初速度为v,相对末速度为0。因乙对地的加速度为a,故甲对乙的相对加速度为-a,根据2(-a)s0=0-v2得a=3 m/s2,因此,乙运动的距离由2as=v2(对地研究)得s=13.5 m,乙离接力区末端的距离为Δs=L-s=6.5 m。
【教学启示】画出运动草图是关键,草图可以给解题有益的启示,甚至起到举足轻重的作用。在教学中,可以师生共同探索解题方法,达到举一反三,触类旁通的效果。
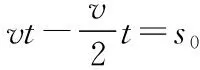
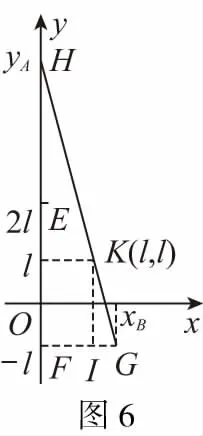
【例5】(2013·全国卷Ⅰ第24题)水平桌面上有两个玩具车A和B,两者用一轻质细橡皮筋相连,在橡皮筋上有一红色标记R。在初始时橡皮筋处于拉直状态,A、B和R分别位于直角坐标系中的(0,2l)、(0,-l)和(0,0)点。已知A从静止开始沿y轴正向做加速度大小为a的匀加速运动;B平行于x轴朝x轴正向匀速运动。在两车此后运动的过程中,标记R在某时刻通过点(l,l)。假定橡皮筋的伸长是均匀的,求B运动速度的大小。
【运动模型】A从静止开始沿y轴正向做加速度大小为a的匀加速运动;B平行于x轴朝x轴正向做匀速运动,开始时R到A和B的距离之比为2∶1,由于橡皮筋的伸长是均匀的,在以后任一时刻R到A和B的距离之比都为 2∶1。
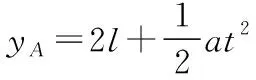
xB=vt②
在开始运动时,R到A和B的距离之比为2∶1,即
OE∶OF=2∶1
由于橡皮筋的伸长是均匀的,在以后任一时刻R到A和B的距离之比都为2∶1。因此,在时刻t有
HK∶KG=2∶1 ③
由于△FGH∽△IGK,有
HG∶KG=xB∶(xB-l) ④
HG∶KG=(yA+l)∶(2l) ⑤
yA=5l⑦
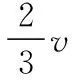
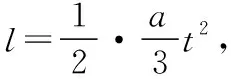
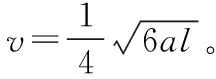
【教学启示】师生共同探索得出任一时刻R到A和B的距离之比都为2∶1是解决问题的关键。本题属于多物体的运动过程,建立起两物体的运动联系,利用几何知识和运动学知识求解。建立正确的模型是解题的关键,熟练应用有关物理知识是解题的核心,正确应用数学知识是解题的重要手段。

