Hadoop环境下基于随机森林的特征选择算法

张 鑫，吴海涛，曹雪虹

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京工程学院 通信工程学院，江苏 南京 211167；3.南京工程学院 康尼机电研究院，江苏 南京 211167)

0 引 言

随着网络数据存储和数据收集能力的快速发展，从海量数据中提取有价值信息成为近年来的研究热点之一。随机森林作为一种常见的机器学习算法[1]，在数据挖掘领域中得到了广泛的应用。而随着数据规模的增大，基于单机的随机森林算法无法满足高维大数据的需求，Google公司的MapReduce分布式计算模型成为一个不错的选择[2]，该模型由Hadoop开源实现。MapReduce分布式计算模型使用简便，具备高扩展、高容错等特点[3-4]，计算架构与随机森林的设计要求相符合，可以方便地实现随机森林算法的并行操作，从而满足对海量大数据快速的计算、分类，相比于传统算法具有良好的加速比和可扩展性。

高维海量的大数据中一个突出的问题就是“维数灾难”，即特征过多的问题。如何从高维的数据中筛选出有用的特征，并利用这些有用的特征进行分类和预测已经成为当今信息技术面临的一大热点问题[5]。特征选择是指从所有特征中评估出最佳的特征子集，使得该特征子集所构建的分类模型达到更好的预测精度[6]。早在1998年，Ho T K提出的随机森林本身就有特征选择这一过程，但是其特征子集是随机选取的，不能保证特征子集里面没有一些冗余的特征对分类产生干扰[7]。2001年，Breiman L在随机森林的阐述中夹杂了内置的特征选择算法[8]，即通过人为改变袋外数据集特征，根据测试集测试准确率变化得到特征的重要性度量，在此基础上选择特征。这种方法相比单纯随机地选择特征，能够获取更佳的特征子集和更好的预测精度，奠定了随机森林特征选择的基础。文献[9]提出的方法从随机森林内置的特征选择出发，采样交叉验证方式获取每棵决策树的特征重要性度量，再根据决策树和集体随机森林预测的一致性得出每棵树的权重，然后加权求和得出最终的特征重要性序列。该算法得出的特征重要性比较准确，但是每一棵树都进行k折交叉验证，对于高维大数据集，计算量太大。

Davies等认为从全部特征中得到最佳特征子集是NP完全问题[10]，要在运算效率和特征子集质量之间把握平衡。特征选择常用的方法主要有Filter方法和Wrapper方法[11]。Filter方法通过给特征赋予一个权重，根据特征的权重对特征进行排序，基于一些准则选取阈值，保留权重大于阈值的特征，淘汰剩余特征，其突出优点是运算效率高，尤其对大数据集，缺点是选出的特征子集质量并不高。Wrapper方法相比Filter方法就复杂了，通过迭代从一个给定的局部最优解出发，不断逼近全局最优解，直接用所选特征子集来训练分类器，根据分类器的性能评估特征子集的优劣，该算法可以选出更恰当的特征子集，缺点是计算效率低。文献[12]在随机森林内置的特征选择基础上融入了Wrapper方法，得到特征重要性排序之后，每次消除最后一个特征重新进行训练分类，直至测试的准确率达到最大值为止。该算法在分类和特征子集选择方面性能良好，但是每次只淘汰一个特征，对于高维大数据集，运算量也是太大。

文中提出的特征选择综合考虑了运算效率和特征选择质量的问题，结合随机森林内置的特征选择算法和文献[9]的算法，并在其基础上进行改进，特征选择的过程在Hadoop的MapReduce计算框架下进行，通过改变袋外数据的每一列特征，根据测试准确率的变化得到每棵树的特征重要性度量，再根据每棵树的可信度得到树的权重，将其与前面的特征重要性度量加权求和，最终得到每个特征的重要性度量。最后在特征重要性排序的基础上选特征时要引入一定的随机性，整个过程在MapReduce计算框架下并行实现，无论是连续型特征还是离散型特征均可使用。

1 随机森林预备知识

随机森林是一种组合分类器，利用bootstrap重采样方法从原始样本中抽取多个样本，对每个采样得到的样本集进行训练，建立决策树，然后把这些决策树组合在一起，形成随机森林，将每一棵决策树的分类结果通过投票进行组合从而最终完成分类预测[13]。大量的理论和实验都证明了随机森林算法具有较高的预测准确率，能够容忍一定的异常值和噪声，因为随机采样和随机特征选择两个随机性的引入不易过拟合。

1.1 决策树

决策树是典型的单分类器，首先对训练集进行递归分析，生成一棵如同倒立的树状结构。在根节点上产生子节点，每棵子节点继续递归产生新的子节点，直到产生节点为叶子节点为止。节点分裂通过比较不同属性分裂后的结果的优劣来选择最优属性分裂产生子树。比较规则的不同产生了多种决策树生成算法，这些算法包括CLS、ID3、C4.5、CART等。

ID3决策树算法通过信息增益准则来选择划分属性，使用信息熵(entropy)来度量样本集合纯度，计算公式如下：

(1)

Ent(D)的值越小，D的纯度越高。利用属性a划分样本集D所获的信息增益(gain)为：

(2)

Gain(D,a)越大，意味着属性a划分带来的纯度提升越大。

然而信息增益准则对属性值较多的属性有所偏好。为了克服这种偏好带来的不利影响，著名的C4.5算法使用增益率选择最优属性，增益率的定义公式如下：

(3)

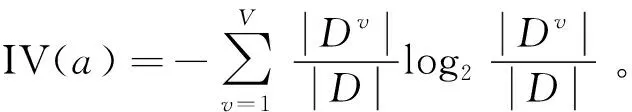
CART决策树用来选择划分属性的是基尼指数(gain)，用基尼值来度量数据集D的纯度：

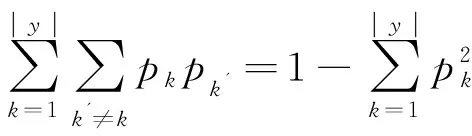
(4)

Gain(D)反映了从数据集D中随机抽取两个样本，其结果不一样的概率。因此，Gain(D)越小，表示数据集D的纯度越高。属性a的基尼指数定义为：

(5)

所以最优的划分属性应该选择基尼指数最小的属性。

1.2 随机森林生成过程

随机森林生成的过程如下：

(1)用bootstrap重采样方法从原始训练数据集中有放回地随机抽取k个新的训练子集，构成k棵决策树，其中未抽到的样本构成袋外数据集。

(2)假设一共有n个属性，在树的每个节点随机抽取m(m≤n)个属性，计算每个属性的信息增益或基尼值，在m个属性中选择分类能力最强的属性来分裂节点。

(3)每棵决策树生长不受限制，也不要做剪裁。

(4)生成的多棵树构成随机森林，使用每棵树的投票对新的样本进行分类[14]。

1.3 随机森林衡量标准

随机森林算法主要用于分类和预测，分类精度accuracy用来衡量随机森林对测试集的总体分类精度，一般而言总体分类精度越高，算法分类效果越好。以二分类问题为例：

(6)

其中，TP表示正确的肯定；TN表示正确的否定；FP表示错误的肯定；FN表示错误的否定。

在随机森林算法中，OOB估计用来估计泛化误差。随机森林在bagging抽样生成训练子集的过程中，一些样本一直没有被抽取，这些样本所占初始数据集的比例为(1-1/N)N。当N取得足够大时，(1-1/N)N收敛于1/e≈0.368，这些样本构成袋外数据集(outside-of-bag data，OOB)。将每一棵决策树的误分率求平均得到随机森林的OOB误分率，就可以得到一个OOB误差估计[15]。

1.4 随机森林内嵌的特征选择算法

Breiman提出过一种隐式的特征选择算法，作为其随机森林算法的一个副产品。该算法认为，当一个重要特征出现噪声时，随机森林分类的准确率会发生很大的变化；而当一个无关紧要的特征发生变化时，分类器预测的精度变动不大。所以通过人为地对测试集中的每一列特征值进行扰动，计算出原始袋外数据与修改后袋外数据预测准确率的差值，即可得出各个特征的重要性度量。假设有B棵树，袋外数据为Loob，特征xj的特征重要性度量基于分类准确率的变化量计算，具体过程如下：

(1)B棵决策树对应B个训练子集，第b棵树记为Tb。

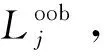
(4)对于b=2,3,…,B,重复步骤1～3。

(5)特征xj的特征重要性度量Dj通过式7计算：

(7)

2 Hadoop环境下基于随机森林的特征选择算法

2.1 算法描述

文中提出的算法是MapReduce计算框架下基于随机森林的特征选择算法，该算法在随机森林本来隐式的特征选择方法的基础上进行了改进。因为每棵树在建模过程中抽样选用的训练子集不一样，树与树之间有一定的差异性，它们对袋外数据预测的准确率不是完全可信，只能说具备一定的可信度，因此可以根据各棵树的预测与集成随机森林的预测的差异计算出每一棵树的权重，再以这些权重对以上各个特征xj进行加权求和，得到最终的特征重要性度量的排序，以便接下来特征选择时更倾向重要的特征。算法步骤如下：

(1)对原始数据集进行bootstrap重采样，有放回地随机抽取k个新的训练子集，在没有特征选择的前提下构成了k棵分类回归树，未抽到的样本构成袋外数据。

(2)使用每一棵树对袋外数据Loob进行预测，在对每个特征xj的特征值进行扰乱后再预测得出每个特征的特征重要性度量Aij(i表示每个特征，j表示每棵树)，同时，计算出集体随机森林预测准确率的变化量Bi。

(3)计算每棵树的权重aj。

(5)将特征按重要性度量从高到低排序，前50%随机选择70%的特征，后50%选择30%的特征，两部分混合后进行节点分裂的特征选取。

算法流程如图1所示。

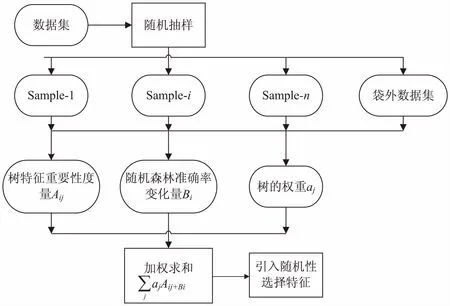
图1 算法流程

2.2 权重度量

各棵树的权重度量也是由袋外数据集测出，具体表现为每棵树对袋外样本集的预测与集体随机森林对袋外样本集预测的一致性，并不是只看每棵树对样本集预测的准确性，这一点充分体现了该算法以集体随机森林的效果作为最重要的衡量点。权重的具体公式如下：

(8)

其中，Treeij表示第j棵树对第i个袋外样本的预测；Foresti表示集体随机森林对第i个袋外样本的预测；S表示袋外样本的个数。

通过表1的7*7一致性度量矩阵展现权重计算的过程。

由表1可得各棵树的权重：a1=0.857，a2=0.571，a3=0.571，a4=0.714，a5=0.571，a6=0.571，a7=0.571。

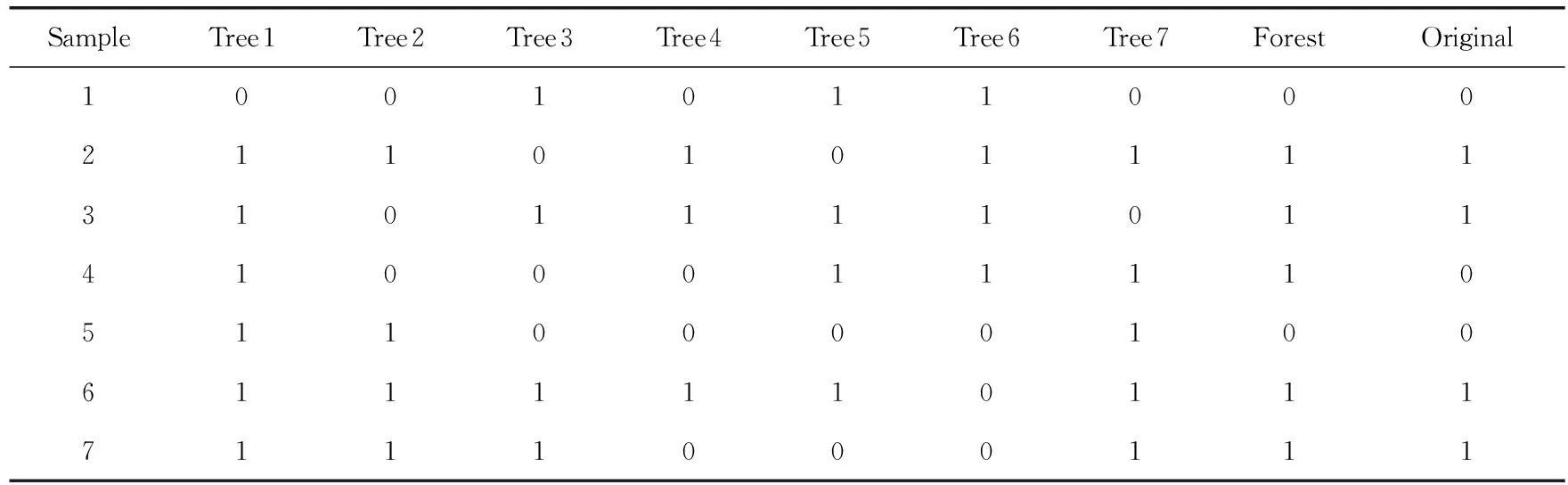
表1 权重度量过程

综上可得最后的特征重要性度量为：

(9)

2.3 算法的MapReduce并行化实现

文中算法的并行化分为两个阶段，一个是训练阶段，一个是测试阶段。训练阶段分为三个步骤：

(1)将训练集分割成一个个数据块block，然后将这些数据块复制并分发到不同的子节点上。

(2)每个子节点上运行的Mapper任务根据其分区Partition上的数据块block建立部分决策树，也就是随机森林的子集，生成一个包含这些树的文件。

(3)从每个子节点所提交的文件中解析出其中包含的决策树，生成输出文件，这些决策树的集合构成了整体的随机森林。

测试阶段分为六个步骤：

根据调查发现，社会道德与自我观、个人观与群体观之间存在明显的既定关系。当社会道德程度越高时，自我观对于价值观与道德判断能力之间的认知能力也将会越强。且当群体观占据主导作用时，个体观具备的认知能力将会受到群体观整体形势的影响而出现对应改变。由此可以发现，价值观与道德判断力之间存在某种特定关系，即自我观与群体观发展程度较高时，价值观与道德判断力基本上可以趋于稳定状态。相对而言，个体自我价值感在此阶段的存在感将会严重下降。在此，笔者建议教师在对青少年进行价值观教育时，必须协调好自我观与群体观之间的关联性与平衡性，尽量不要出现某种倾向性过强的情况。

(1)将袋外数据集的一列列特征值打乱，改变后的数据集与原始的袋外数据集拼装在一起，形成一个大测试集。

(2)将这个大测试集分割成独立的数据块block，然后把这些数据块复制并分发到不同的子节点上。

(3)各个子节点上运行的Mapper任务根据上一阶段建立的随机森林模型对测试集中数据的类型进行预测，由多数投票表决来预测类别。

(4)对所有Mapper任务产生的预测进行汇总，生成最终的预测文件，预测文件包含各棵树的预测结果，即形成一个i*k*(j+1)的矩阵，i为特征个数，j为树的个数，k为袋外数据集的样本个数，最后一列为随机森林预测结果。

(5)将生成的大矩阵按照袋外数据集样本个数k进行行的分割，从而得到每棵树对应每个特征打乱后的测试集的预测情况。

(6)利用以上得到的值计算特征重要性度量，然后进行特征选择。

3 仿真实验

3.1 实验环境

采用UCI数据库中的KDD Cup99数据集，该数据集样本数4 000 000个，特征个数为42，现在将其划分为互不重叠的4组数据：D1、D2、D3、D4，如表2所示。

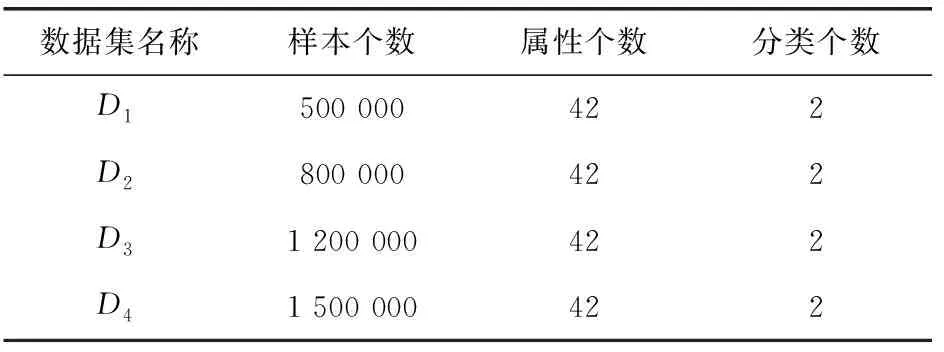
表2 实验数据集

实验中参数设置如下：maxDepth=unlimited，numFeatures=0.5NumAttrs，numTrees=80。其中maxDepth表示决策树最大深度，numFeatures表示选择特征的个数，numTrees表示随机森林中决策树的个数。

3.2 评估指标

accuracy用来衡量随机森林对测试集的总体分类精度。实验采用accuracy和加速比S来评估算法的性能，计算公式如下：

(10)

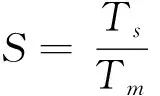
(11)

其中，TP表示正类被正确分为正类的数量；TN表示负类被正确分为负类的数量；FP表示负类被错误分为正类的数量；FN表示正类被错误分为负类的数量。Ts表示单机上实验所花的时间；Tm表示Hadoop平台m个节点上所花的时间。

3.3 实验结果

表3展示了文中随机森林算法、传统随机森林算法以及文献[12]的Wrapper算法的分类精度对比。

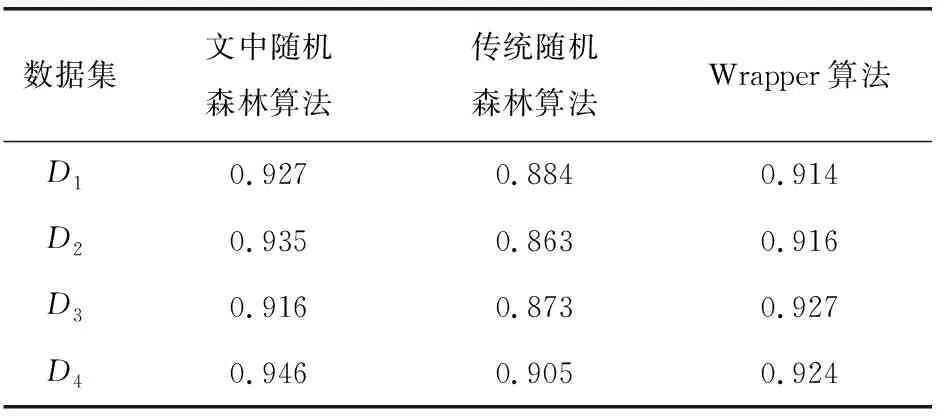
表3 分类精度对比

从表3可以看出，文中随机森林算法在D1、D2、D3、D4四个数据集上训练和测试得到的分类准确性比传统的随机森林算法有了一定的提升，在D2数据集上分类精度的提升达到了7.2%。因为在建树特征选择的过程中，更倾向于选择重要的特征，减轻了冗余特征对决策树模型的干扰，从而提升了随机森林的分类精度。此外，与Wrapper算法相比，发现文中算法除了在D3数据集上比Wrapper算法低了1.1%，其余都高于后者。因为文中算法在得出特征重要性排序的基础上又引入了一定的随机性，并不是完全选择重要性排序靠前的那些特征，这样可以减少决策树之间的相关性，减少过拟合，从而一定程度上提高最终随机森林的分类准确性。

文中算法的加速比曲线如图2所示。

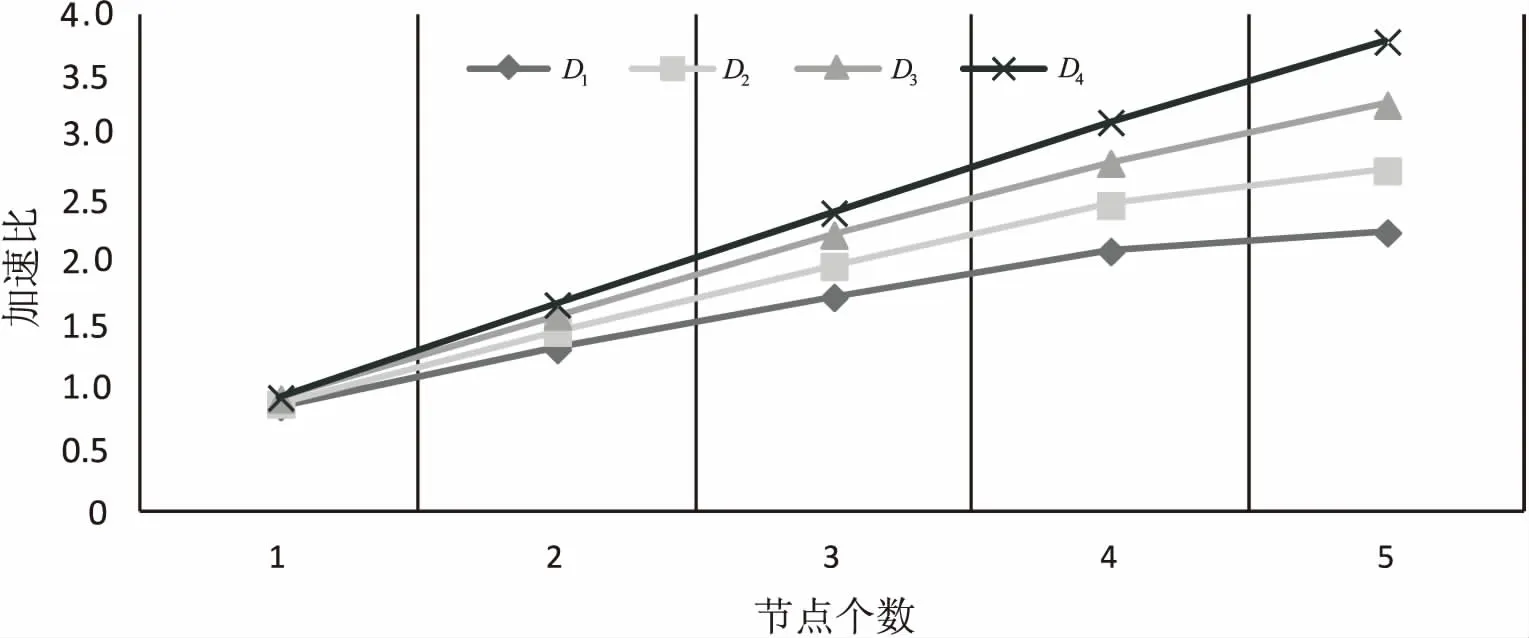
图2 文中算法的加速比曲线

可以看出，当节点数为1时，加速比小于1，即Hadoop环境下的运行速度比单机运行的速度还慢。这是因为启动Hadoop运行环境需要一定的时间，随着节点数量的增加，对数据的处理速度加快，加速比提升。而当数据集较小时，加速比不是很理想，因为处理数据的时间较短，相对来说节点之间通信所花的时间较长。而随着数据集渐渐增大，节点之间通信开销的时间远远小于数据处理的时间，加速比得到大幅度提升，甚至接近线性增加，特别是在D4数据集上，加速比的增加量分别为0.75、0.74、0.73、0.65，基本上贴近线性增加。加速比实验说明并行化的随机森林更适合大数据量，相比于传统单机模式下的随机森林算法，文中算法在处理高维大数据上运行效率明显提高。

4 结束语

提出了一种Hadoop环境下基于随机森林的特征选择算法，该算法在MapReduce计算框架下完成，对随机森林算法中内置的特征选择方法进行了改进。通过对袋外数据集每一列特征的干扰得到每棵树对应每个特征的重要性度量，再将这些度量与各个决策树的权重加权求和，得到最终各个特征的重要性度量。在特征选择的过程中，一方面倾向重要性较大的特征，另一方面兼顾选择的随机性，减少决策树之间的相关性，从而减少过拟合。实验结果表明，该算法相比传统的随机森林算法或Wrapper特征选择算法，分类性能得到了一定程度的提高；同时，由于MapReduce并行计算的应用，使得该算法对高维海量数据的处理有所提高，具备明显的高效性和可扩展性。