基于稳定性的不锈钢地铁底架焊点布局改进
2018-07-24刘新武孙丽萍王玉艳王萌赵阔
刘新武,孙丽萍,王玉艳,王萌,赵阔
(大连交通大学 交通运输工程学院,辽宁 大连 116028)
0 引言
近年来,在城市轨道交通中,地铁已经是一个城市经济能否快速发展的重要标志.我国的地铁车辆车体主要材料是不锈钢和铝合金.不锈钢车体强度高、重量轻、耐腐蚀性强,更因免涂装、耐高温、防火性强、维护少、全寿命周期成本低等优点被广泛应用[1].目前,轨道车辆技术人员主要从车体制造、点焊工艺和力学性能等方面对不锈钢车体进行研究[2-3].不锈钢材质焊接时产生的热量会积聚于焊缝区域,不能很快散失,容易产生焊接变形.为了减小焊接变形和防止高温下不锈钢材料机械性能的下降,地铁不锈钢车体结构的连接多采用电阻点焊方式,上万个焊点密布于车身[4].地铁车体主要由底架、侧墙、车顶、端墙和司机室等几个部分组成.为了保证车体能正常工作,车体中的每一个构件或组成部分不仅要满足强度和刚度要求,还要有足够的屈曲强度以满足稳定性要求.
在结构力学研究领域,稳定性一直是人们不可忽视的一个重要问题.随着科学技术的发展,高强度材料的不断涌现和应用,材料强度和刚度基本能够得到保证,而结构的稳定性问题更加突出[5].近年来,随着轨道车辆的不断发展,一些人对轨道车辆的稳定性进行了深入研究,如:岳译新等人对某铝合金地铁进行稳定性计算[6];姚亚涛等人分析了速度为 200 km/h不锈钢车体稳定性[7].稳定性分析亦是屈曲分析,屈曲分析分为线性屈曲和非线性屈曲两类,发生失稳后的变形相对于原尺寸不大的问题叫做线性屈曲,失稳后变形较大的屈曲问题称为非线性屈曲. 利用有限单元法求解屈曲,计算速度快,精度高,能在一定程度上预测屈曲强度.对于线性屈曲问题,工程上常采用的方法有 LANCZOS、矢量迭代法等,对于非线性屈曲问题,工程上常用的方法是弧长控制法.
本文以某地铁车体底架为研究对象,进行线性屈曲分析,并且对底架失稳严重区域的焊点布局进行改进.选择底架为研究对象,一方面是因为底架大量焊点的存在,可能会对稳定性造成一定的影响.另一方面底架作为主要承载结构,其安全性尤为重要.
1 线性屈曲分析理论基础
薄板屈曲的控制微分方程为[8]:
(1)
(2)
(3)
式中:Px、Py分别是x、y方向的均匀分布的面向压力;ω为薄板的挠度;D为薄板的弯曲刚度.
将式(2)、(3)代入式(1),便可求出微分方程,不同的薄板支撑结构对应不同的边界条件,解得的上述方程不同.但在线弹性的屈曲分析中,结构屈曲的临界载荷可用下面的公式表示:
Pcr=λP0
(4)
式中:Pcr为薄板的临界载荷;P0为作用载荷;λ为屈曲因子.
λ的计算公式为:
([KL]+λ·[KG])·{δ}=0
(5)
式中: [KL]为结构的总体弹性刚度矩阵; [KG]为结构总体几何刚度矩阵; {δ}是特征向量位移.
由式(4)可知,在求解屈曲因子时,结构的临界载荷是一定的,所施加的作用载荷可以是任意的.作用载荷越大,所求得的屈曲因子越小,只是它们的乘积保持不变.本文利用 HyperWorks软件中的 LANCZOS方法求解特征值即屈曲因子.
2 底架结构简介及有限元模型的建立
本文选择某地铁中间车的底架为研究对象,所研究的底架由牵引梁、枕梁、缓冲梁、边梁、横梁、波纹地板及纵向梁等组成.其中,牵引梁和枕梁的材质为低合金、高强度钢,且不易发生屈曲,不是本文所考察的重点.此底架两枕梁之间无贯通的中梁,作用在底架上的力均由波纹地板、边梁和中间分布的许多横梁来承担,横梁与横梁之间的距离为 0.5 m左右.底架多处采用点焊连接,横梁与波纹地板、边梁之间的连接为点焊,枕梁、缓冲梁与波纹地板之间也为点焊结构.由车体钢结构静强度试验表明,纵向波纹地板能承受三分之一以上的总纵向拉伸和压缩力[9].
基于底架的 CAD设计图纸建立有限元模型,如图 1所示.在仿真模型的建立过程中,需要综合考虑车体结构的几何形状、受力特点等.采用大小为 20 mm左右的壳单元进行模拟,采用 CWELD单元模拟焊点,部分连接采用 RBE2刚性单元,整个底架单元数量为 416816,节点总数为 422871.在四个空气弹簧座处约束垂向线位移,以均布力的方式在两个冲击座中间板上各施加大小为 800kN的纵向压缩力,方向相反,并且以重力加速度的形式施加垂向载荷.图 2为约束和纵向力施加位置示意图.

图1 底架有限元模型

图2 约束与纵向力施加位置示意图
3 底架的屈曲分析
3.1 底架屈曲分析
首先对底架模型进行有限元静力求解,求出最大的Von Mises应力以及对应的应力最大位置.得到静力结果后,继续求解前10阶的线性屈曲特征值,求解后各阶屈曲因子如表 1所示,失稳部位均为枕梁附近边梁处波纹地板,各阶失稳的具体位置如图 3所示,前四阶屈曲振型如图 4所示.

表1 底架屈曲分析结果
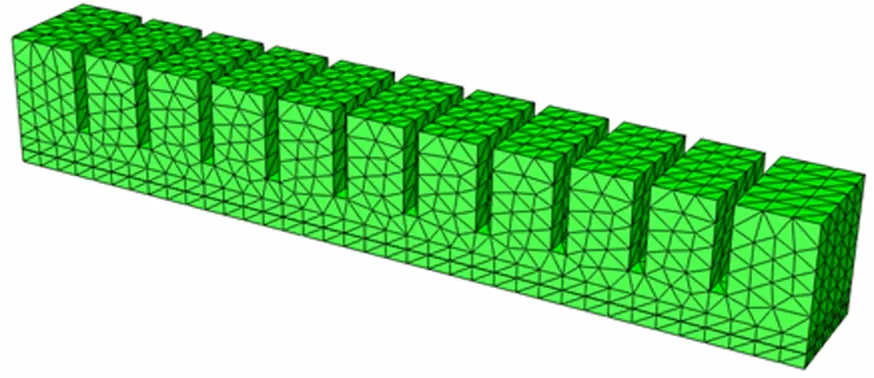
图3 前十阶失稳顺序

(a)一阶屈曲模态
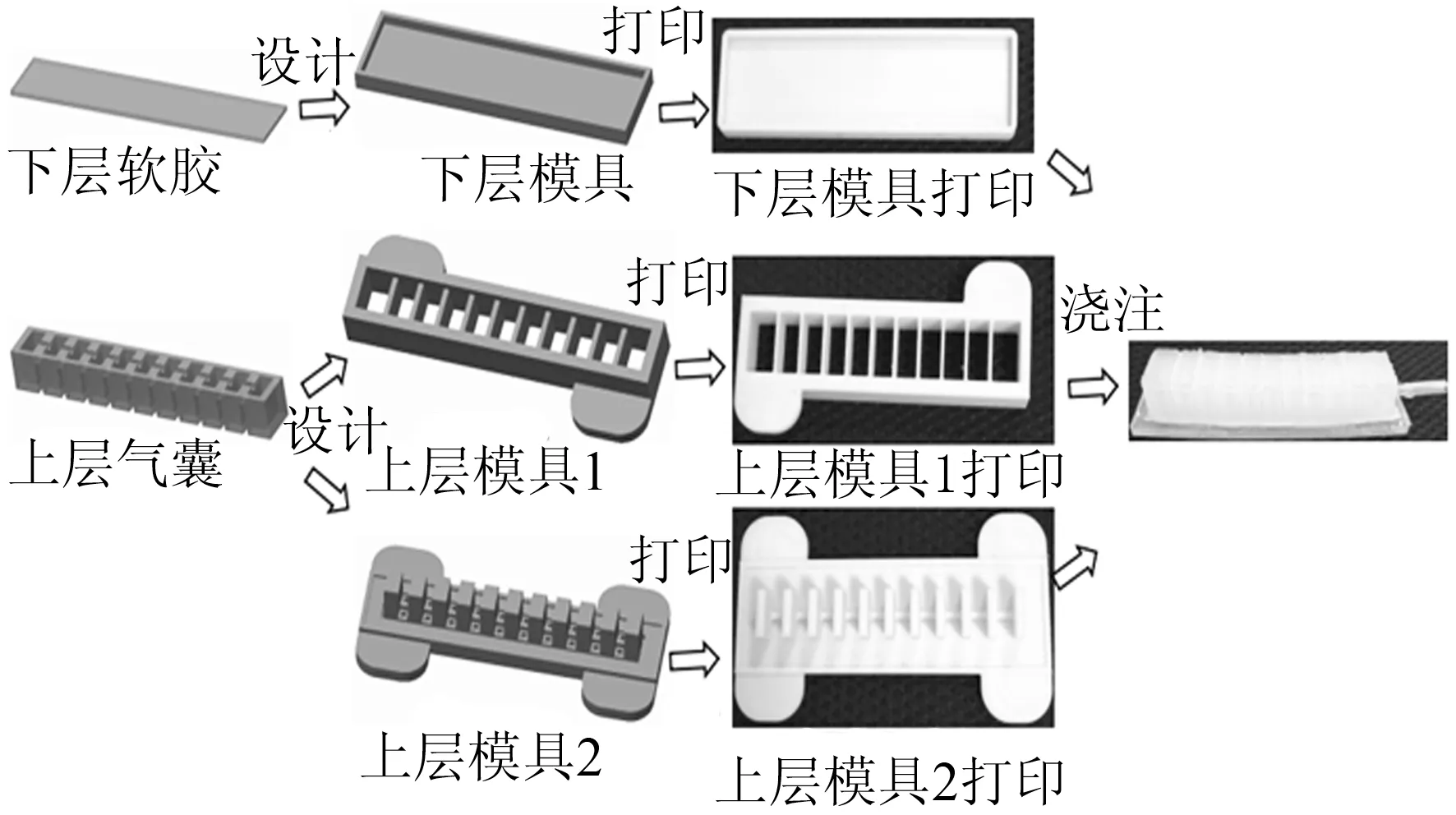
(b)二阶屈曲模态
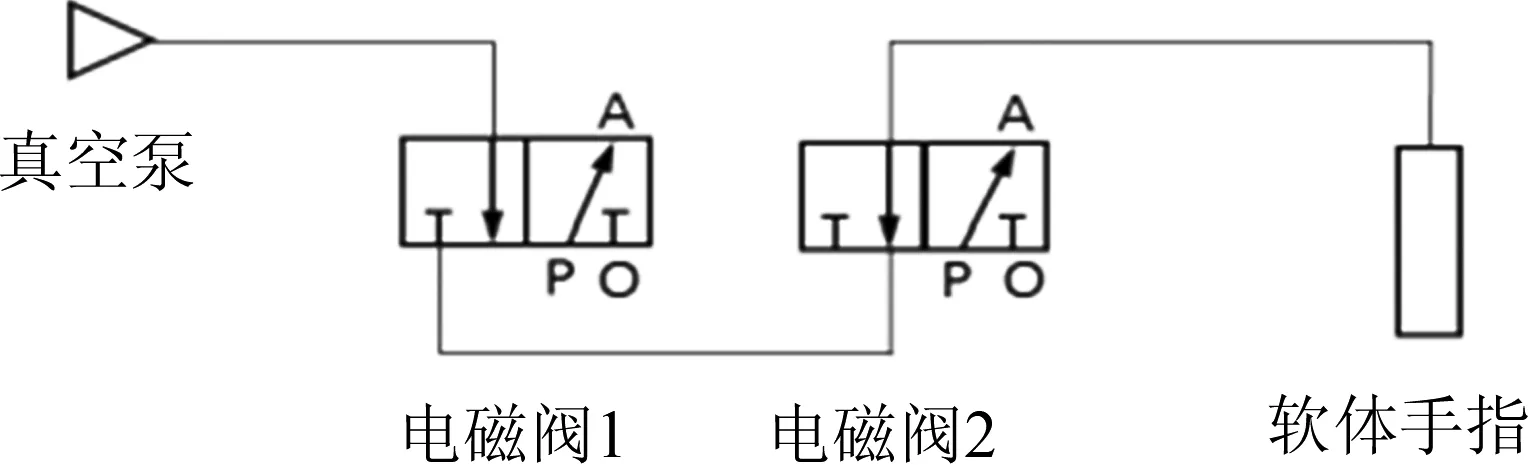
(c)三阶屈曲模态

(d)四阶屈曲模态
3.2 屈曲结果分析
由表1可知,第一阶屈曲因子为0.942 3,根据公式Pcr=λP0,可以计算出对应的临界载荷Pcr为753.86 kN.同理,可知底架在临界载荷Pcr为755.68 kN下发生第二阶失稳,以此类推,我们可以得到前十阶的临界载荷.随着屈曲因子的增大,对应的临界载荷也在增大.由屈曲模态图和失稳顺序图可知,底架容易失稳部位是两个枕梁附近的边梁处波纹地板,从失稳顺序图可以看出,在前十阶失稳过程中,失稳顺序以底架纵向中性面呈对称分布.除边梁处的局部波纹地板外,其他位置的波纹地板没有发生屈曲,如:中间横梁与地板连接处稳定性较好.故对失稳部位处的焊点布局进行合理改进.
4 底架焊点布局改进
4.1 焊点布局改进方案
从材料力学及结构设计的角度分析,发生屈曲的一个很重要的原因是自由面积过大,约束不足.因此,在失稳部位应该加密焊点,同时减少波纹地板与补强板之间的焊点.具体实施方案为,依据铁路车辆及其部件的焊接标准 EN 15085-3-2007所提供的电阻点焊时焊点间距的最低设计标准,具体设计标准见表 2.在前十阶屈曲失稳部位(即枕梁附近)将初始 50mm间距设计的焊点改为 40 mm间距,并且补强板与波纹地板连接处的焊点由初始间距 50 mm增大为 100 mm.如图 5所示.

表2 焊点间距最低设计标准 mm

(a)补强板与地板间焊点改进

(b)边梁与地板间焊点改进
4.2 改进方案结果分析
通过重新计算改进后的底架模型.结果表明,改进后方案与初始设计方案在强度和刚度上变化不大,均满足设计要求.改进后求得的前 10阶屈曲因子如表 3所示.
由表 3可以看出,改进后第一阶屈曲因子为 1.074 3,根据公式可求出对应的临界载荷为 859.44 kN,相比于初始方案,临界载荷增加 105.58 kN.改进后第二阶屈曲因子为 1.075 2,临界载荷为 860.14 kN,相比于初始方案,临界载荷增加 104.46 kN,后几阶屈曲因子相比于初始方案均有增加(前 10阶的临界载荷均增大 100 kN左右),底架的屈曲因子整体提高.波纹地板的稳定性增强.第一阶失稳部位变为底架中间位置的边梁处波纹地板.总之,两个枕梁之间的边梁处波纹地板与边梁之间的焊点布局对于整个底架尤为重要,需要工程人员通过大量实验,找出最佳焊点位置,从而保证底架的稳定性.
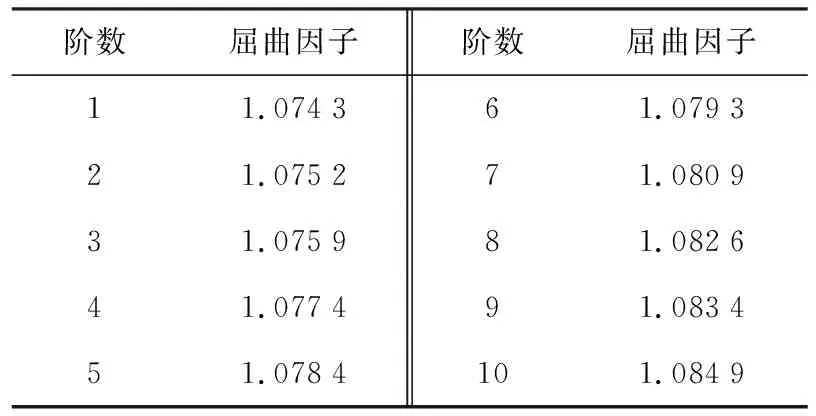
表3 改进后屈曲分析结果
5 结论
本文以某不锈钢地铁车底架为研究对象,对其进行屈曲分析,从稳定性的角度得出以下结论:
(1)底架整体稳定性较好,只是局部会发生屈曲现象,容易发生失稳的位置为枕梁附近边梁处的波纹地板.与中间横梁连接的波纹地板不易发生屈曲,牵引梁端部的补强板与波纹地板的焊点过多,适当增大焊点间距,对静强度以及屈曲没有影响,可去掉冗余焊点;
(2)对枕梁附近的波纹地板进行局部改进,能很好的提高屈曲因子,明显增大临界载荷,说明焊点布局对于稳定性有重要作用,故对于底架的整个波纹地板,合理优化焊点布局,是设计人员需要考虑的重要问题.
