基于代理模型的焊接构架纵梁优化设计
2018-07-24高月华赵丹谢素明刘其鹏
高月华,赵丹,谢素明,刘其鹏
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028: 2. 大连交通大学 土木与安全工程学院,辽宁 大连 116028)
0 引言
铁路车辆的发展制约着轨道交通系统的推广,随着我国科学技术的研究使得转向架的发展越来越迅速,而转向架又是车辆的重要组成部件,转向架在运行速度、曲线通过能力、动力学性能和舒适性等列车运行指标的改善方面做出了重要贡献,并且其具体结构的差别对车辆运行也很有影响.构架作为转向架的支撑骨架,其作用不仅要在车辆运行过程中支撑车体,而且传递车轮与车体相互间的各种纵向力、横向力和垂向力.由此可见,轨道车辆的运行品质和行车安全直接受到转向架构架可靠性的影响,因此,对转向架构架进行结构优化设计是十分必要的.
目前,学者们开展了一些转向架结构的优化研究工作.Park[1]在优化模型中加入疲劳损伤约束,应用人工神经网络和遗传算法进行优化,最终实现转向架的轻量化设计.Gao等[2]用Kriging近似模型技术,提出考虑焊接疲劳损伤约束的转向架焊接构架优化设计方法,最终实现构架质量减轻9.2%.聂春戈[3]采用变密度方法,以转臂为研究对象建立了以结构的总柔度为目标函数,体积为约束的拓扑优化模型,并应用HyperWorks进行了减重设计.熊德伟[4]采用变密度法,以结构应变能最小为优化目标,以单元密度为设计变量,利用OptiStruct软件对齿轮箱吊座进行拓扑优化,并在拓扑优化的基础上设计出新的吊座.李超[5]基于变密度法,在特定工况下采用OptiStruct软件对转臂进行了拓扑优化设计,最终优化结构不仅von-Mises应力值降低,而且其质量比原结构下降8.43%.
本文以城际动车组焊接构架纵梁为研究对象,首先在满足静强度条件下进行了结构拓扑优化设计,然后应用等效结构应力法计算焊缝疲劳强度,并引入基于代理模型的近似序贯优化方法进行了抗疲劳尺寸优化设计,最终达到转向架焊接构架轻量化的目的.
1 构架纵梁的拓扑优化
本文转向架为无摇枕、转臂式轴箱定位结构.转向架构架主要由侧梁、横梁、纵梁以及各种吊座组成(见图1(a)).纵梁连接横梁与横向止挡等重要承载部件,起着重要的连接与支撑作用,其结构如图1(b)所示.基于有限元分析确定纵梁为优化对象,为获得更为理想的拓扑优化结构,采用三维实体网格填充其内部,获得新的有限元实体模型如图2所示.
图1 转向架构架的结构

图2 纵梁实体有限元模型
依据静强度分析结果,在进行拓扑优化的过程中只考虑对纵梁结构影响较大的载荷工况,工况详见表1.根据静强度结果构建优化模型如式(1)所示.

表1 静强度工况
(1)
式中:xi是设计区域的单元密度;V0为设计区域的总体积,σ1为单元1在工况1下的应力值;σ2为单元2在工况2下的应力值;d1为节点3在工况1下的横向位移值;d2为节点3在工况2下的纵向位移值;各单元和节点的位置如图3所示.

图3 单元、节点选取示意图
基于给定的拓扑优化模型,应用OptiStruct软件进行求解.为获得理想的优化结果,对优化模型施加模式组的二平面对称约束.为避免迭代步数过多,限制最大迭代次数为50.经过25次迭代得到最优结果.取密度阈值为0.3时纵梁的拓扑优化结构如图4所示.新优化结构仍为箱体结构且结构完整,内侧立板拓掉部分材料,内部筋板位置更加居中,如图5所示.新结构质量由63.2 kg减小为57.7 kg,减重约8.7%,在满足静强度的条件下,实现了结构的轻量化.

图4 密度阈值0.3时纵梁拓扑优化结构
图5 纵梁新结构
2 基于代理模型的尺寸优化
2.1 焊接构架纵梁的尺寸优化模型
本文中的转向架构架为焊接结构,交变载荷作用下该结构的破坏往往表现为焊缝的疲劳破坏,因此在进行尺寸优化设计时,焊缝疲劳寿命是一个不可忽视的质量指标.
针对纵梁结构,板厚作为设计变量,考虑静强度、刚度和疲劳损伤约束,构建优化模型如式(2):
(2)
式中:xi(i=1,2,3,4)为设计变量,即纵梁箱型结构的各个板厚;M为纵梁的总质量;σ1为表1中工况3下的最大von-Mises应力值;d1为节点3在表1中工况1下的横向位移值;Di为纵梁结构相关焊缝处的最大疲劳损伤值(详见2.2.2节).ximin和ximax为其上下限,详见表2.
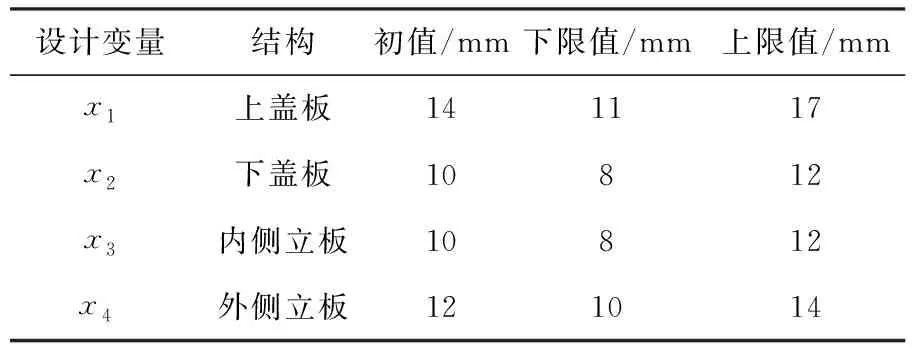
表2 设计变量信息
2.2 焊接构架纵梁的焊缝疲劳寿命分析
2.2.1 等效结构应力法
对于焊接结构,Dr. Dong提出一种评估焊缝疲劳的方法,即等效结构应力法[6-8],该方法采用网格不敏感的结构应力计算方法及一条主S-N曲线预测焊接结构焊缝上的疲劳寿命,很好地解决了名义应力法所遇到的上述困难.因此本文采用等效结构应力法对构架纵梁处焊缝进行疲劳寿命分析.
该方法预测焊接结构焊缝疲劳寿命的计算公式为
ΔSs=Cd·Nh
(3)
(4)
式(3)、(4)中:Δσs为结构应力反映了应力集中的影响;t反映了板厚度的影响,I(r)反映了载荷模式的影响;m=3.6,Cd及h为主S-N曲线试验常数,由ASME标准提供,N为循环次数.
2.2.2 纵梁结构的焊缝疲劳累积损伤
本文中纵梁结构的焊缝疲劳累积损伤的计算考虑了两方面载荷情况,一是整体构架的载荷,另一种为设备载荷.整体构架的载荷包括垂向动态载荷、垂向准静态载荷、横向准静态载荷和扭转载荷,并依据UIC515-4标准分3阶段进行加载.设备载荷主要考虑了对纵梁结构影响较大的电机和齿轮箱的载荷.疲劳载荷工况详细信息见表3.基于表3中的载荷信息及循环次数要求,应用等效结构应力法将两方面载荷分析所得的焊缝疲劳累积损伤相加,并将疲劳损伤的最大值作为式(2)中的Di值.

表3 疲劳载荷
2.3 代理模型优化技术
对于给定优化模型式(2),焊缝的最大疲劳损伤值Di与设计变量之间存在高度的非线性关系,优化难度较大,因此本文应用代理模型近似优化技术进行求解.
典型的近似建模方法包括响应面模型、Kriging模型[9]、径向基神经网络方法等.本文采用Kriging模型,Kriging模型是一种估计方差最小的无偏估计模型.它能够提供一种精确的插值,从统计意义上说,是从变量相关性和变异性出发,在有限区域内对区域化变量的取值进行无偏、最优估计的一种方法.基于Kriging模型的序列近似优化流程如图6所示.该优化方法具有自适应功能,能够基于小样本进行有效的优化设计,从而提高计算效率.

图6 基于代理模型的近似优化方法流程
2.4 优化设计结果
依据给定优化模型应用最优拉丁超立方法[10]获得15组样本数据,并进行有限元分析计算得到相应的响应值,见表4.
本文借助于Isight软件构建代理模型并执行优化设计.基于表4中的样本数据,针对质量、应力、位移和焊缝疲劳损伤指标,构建4个Kriging模型,并基于Kriging模型结合多岛遗传优化算法进行优化设计.
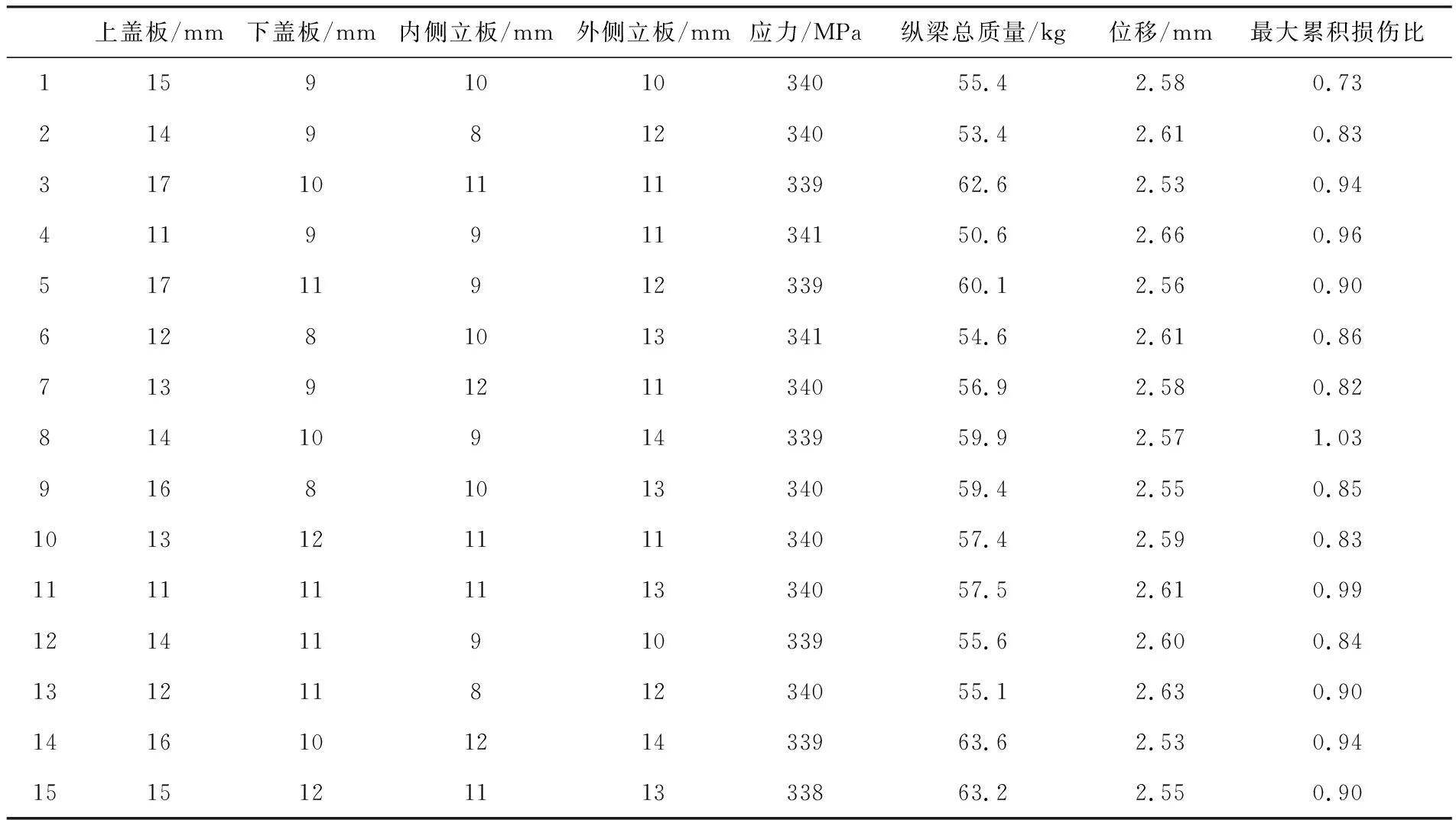
表4 设计变量的样本数据及响应指标
依据图6的近似序贯优化方法,在优化过程中不断地添加样本数据直到代理模型所得的优化结果与有元分析结果吻合精度较高,则优化结束,优化结果见表5和表6.

表5 最优设计结果
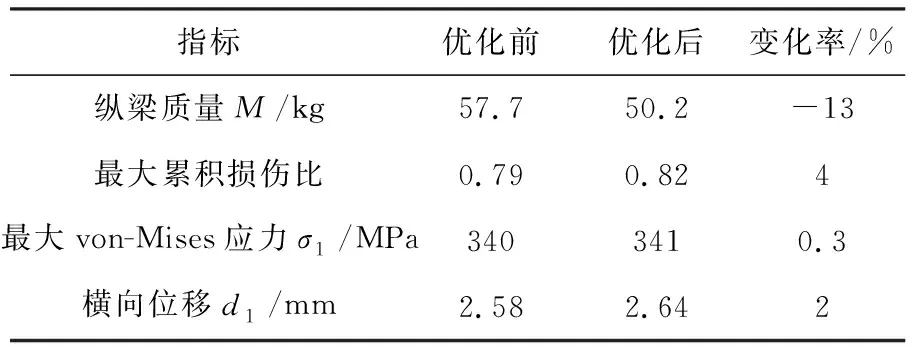
表6 最优设计优化指标
由优化结果可知,纵梁的板厚都有所减少,虽然最大疲劳累积损伤、最大von-Mises应力和位移值都有所增加,但在满足约束条件下重量减少了7.5 kg,约13%,实现了纵梁结构的有效轻量化.
3 结论
本文以城际动车组焊接构架的纵梁为研究对象,对其进行了拓扑优化和抗疲劳尺寸优化研究,总结如下:
(1)针对焊接构架的纵梁结构,在满足静强度约束的条件下进行拓扑优化,获得新的优化结构减重约8.7%;
(2)在新拓扑结构的基础上,构建了以静强度、刚度和焊缝疲劳损伤为约束的轻量化模型,应用等效结构应力法进行焊缝疲劳寿命分析,并引入基于Kriging代理模型的近似序贯优化方法进行优化设计.尺寸优化后结构再次减重约13%;
(3)经过拓扑优化设计和抗疲劳尺寸优化设计,焊接构架纵梁结构由63.2 kg减为50.2 kg,减重约20.6%.本文工作对焊接构架纵梁进行了有效的轻量化设计,为焊接构架的设计提供了重要参考.
