新型板桩承台式直立堤波压强试验研究

徐宇航，陈国平，严士常，许 凡，王 聪

(1.河海大学 港口海岸与近海工程学院，南京 210098；2.河海大学 海岸灾害及防护教育部重点实验室， 南京 210098)

随着社会经济与筑港技术的发展，受限于地质条件及已有建筑物的制约，越来越多的新型结构形式被利用到深水防波堤以及人工岛围垦护岸工程建设中。板桩承台式直立堤是一种新型的深水驳岸结构，直立堤后部使用板桩墙作为墙后回填土挡土结构，板桩前设斜桩，通过上部混凝土承台连接与板桩墙形成整体，共同承担结构所受竖向力及水平力。同时为减少越浪量以及节约工程造价，承台上向海侧设置挡浪墙，必要时挡浪墙顶部设置一向前突出的“檐”(以下称之为挑檐)，使得波浪水体和水花受到“檐”的压制和反射，水体被挑回堤前[1]。类似挑檐的设计易于施工且效果甚好，已常见于斜坡堤上挡浪墙设计中，更进一步衍化出了各种类型的反弧形挡浪墙[2-3]。国内外学者已对直立堤和各种类型的反弧形挡浪墙前波浪力做了系列相关研究[4-9]并取得了一定的研究成果，但对于直立式建筑物顶部设置挑檐状况下波浪力的作用机理研究相对不足，对于板桩承台式直立堤这一结构研究则更为少见。

挑檐的设置能够有效的减少越浪量，但是挡浪墙前设置挑檐是否会增大局部波压强值而对结构安全造成较大的不利影响是研究与设计者所共同关注的问题，本文针对这一问题结合实际工程断面进行波浪模型试验，对波浪作用产生的波压强分布和规律做进一步研究。

1 试验概况

本次试验在波浪水槽中进行，水槽长80 m，宽1 m，高1.5 m。水槽工作段在纵向被分隔成0.5 m的两个部分，试验时模型放在外侧部分进行试验，另一部分用以扩散二次反射波能。水槽两端均铺设消浪缓坡，以减少波浪的反射。波浪水槽一端采用南京水利科学研究院研制的电机式推板造波机，可产生试验所需要的不规则波，试验时靶谱采用标准JONSWAP谱，谱峰升高因子γ=3.3。

试验断面模型依托于实际板桩直立堤护岸工程，模型使用有机玻璃材料制作，采用1∶28的比尺，模型前模拟实际地形为1∶45的缓坡。试验时采用北京水科院生产的波压力监测系统，采样频率为100 Hz，波压力采集探头从挡浪墙挑檐下端开始沿断面向海侧方向布置，试验断面模型布置及波浪压力测点布置见图1。

1-a 试验断面波浪水槽布置图1-b 试验断面模型及波浪压力测点布置图1 断面模型布置及波浪压力测点布置图Fig.1 The test section model and wave pressure measuring point arrangement

试验根据实际工程设计水深波浪要素，经过比尺换算，采用的水深分别为d=11.6、12.9、20.9和26.4 cm，实际率定有效波高Hs= 7.9、11.4、12、12.7、14.0 cm，波周期Tm= 1.3、1.6、1.9 s。试验时每组试验工况造波时间为300 s，每组波系列共有约150～230个波，每次造波待水面平静后对压力传感器进行清零后继续造波，每组工况重复3遍。试验处理时每组工况取每遍采集到的波压强的前1/3个大值的平均值作为波压强特征值进行分析，并以Pc表示。

2 试验结果分析

本次试验通过安装在试验模型表面的波压力传感器进行数据采集，水深足够时，模型前波浪形态主要以立波为主，仅在大波时发生破碎。试验结果分析表明，采集到的波压强时间过程具有明显的周期性特征，波浪作用在结构物上的波压强值主要由一个在波浪作用瞬间产生的冲击压强和一个随波峰面高度变化产生的缓变压强两个部分组成[10-11]。

2.1 波压强沿模型表面分布规律分析

本次试验实测波压强沿模型表面的分布主要分为两个部分，一部分是波压强沿模型迎浪面高程方向的分布，对应于压力测点布置图中的1#～8#和15#～19#测点，各测点距静水位的距离用z表示，定义静水位以上方向z为正。另一部分是波压强沿模型承台底部水平方向的分布，对应于压力测点布置图中的9#～14#测点，各测点距承台到板桩墙连接处的距离用x表示，定义测点位置向造波机方向为正。图2给出了试验水深d=26.4 cm时，相对波长L/d=7.06的波压强统计值Pc的分布，其中Hs/d表示相对波高，Pc/(γHs)表示相对压强，z/d表示以静水位为坐标原点测点距离静水位的相对高度，x/B表示测点距承台与板桩墙连接处的相对距离。

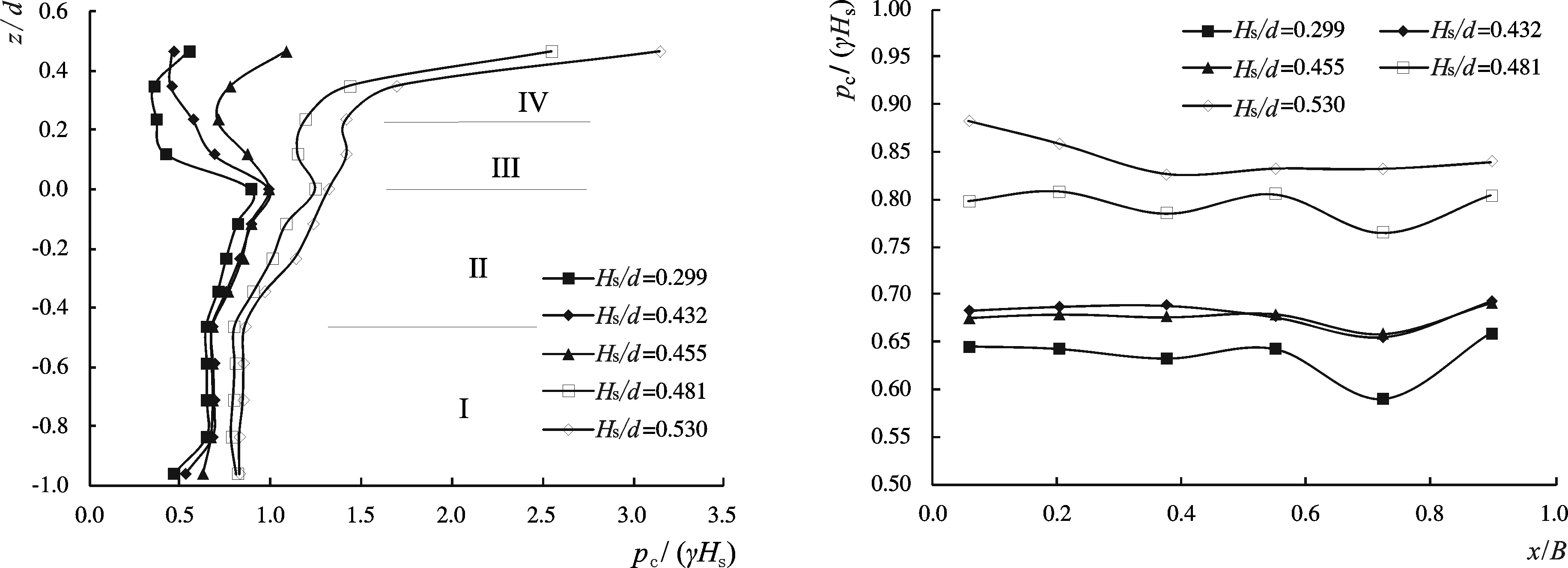
2-a 波压强高程方向分布2-b 波压强水平方向分布图2 不同波高下波压强分布Fig.2 Wave pressure distribution under different wave heights

由图2-a可知，在试验水深d=26.4 cm时，波压强沿高程方向上的分布主要分为四个部分，且相对压强值随相对波高的增大而增大。第I部分为在静水位以下的板桩墙部分，其上的波压强值沿高度方向的分布几乎不变，可能的原因是由于前置挡浪墙和承台的庇护，直接作用在板桩墙上的波浪较小，波压强主要由挡浪墙前波峰面升高而产生的缓变压强所致。第II部分至第III部体现为波压强随着相对高度z/d的增加而先增大后减小，在静水位处为波压强最大值，其波压强分布趋势同各家直立堤波压强计算理论分布基本吻合。第IV部分由于挑檐的存在，使得本应随着z/d的增加而减小的波压强值反而逐步增大。这是因为由于挑檐的阻挡，使得本应随着波浪水体升高而造成的波浪动能向势能转化这一过程受到阻碍，波浪撞击能量较大，从而导致距离挑檐越近的部位波压强值反而增大。而且受挑檐的影响，波压强值增大的部分范围随着波高的增大而增大，当波高Hs/d=0.530时，第III部分几乎消失，静水位以上波压强随着z/d的增加而增大。由图2-b可知，各相对波高下模型承台底部波压强沿水平方向的分布变化幅度较小，波压强沿水平方向分布几乎不变，因此实际工程中当水深超过直立堤承台底部一定高度时，承台底部波压强均可视为均匀分布进行计算。

2.2 入射波相对波长对波压强的影响

波浪的波长作为设计波要素的重要参数之一，其对描述波浪的形态以及分析波浪对结构物的作用具有重要意义。当入射波波高一定时，波长的变化不仅影响到波浪波峰面作用到建筑物的角度，从而导致作用在结构物上波压力的不同。而且当波长较长时，长周期波具有将挑檐下部空间填满的趋向，导致后面的波浪直接越过堤顶，挑檐并未起到挑浪的作用，从而使得挑檐端部附近的波压强反而有所减小。图3给出了试验水深d=26.4 cm，相对波高Hs/d=0.530时，模型各测点相对压强与相对波长之间的变化关系。从图中可以看出，各测点处在相对波长L/d=9.04时的波压强值明显大于相对波长L/d=7.06时，表明波压强随相对波长的增大而增大。但当相对波长L/d=10.97时，各测点波压强却并没有增大，同时挑檐附近的测点波压强值反而有所减小。图4分别给出了入射波周期不同下挑檐与挡浪墙连接处的波压强值及越浪量的变化关系，可以看出对应于越浪量的明显增大，挑檐与挡浪墙连接处的波压强值出现显著性的减小。

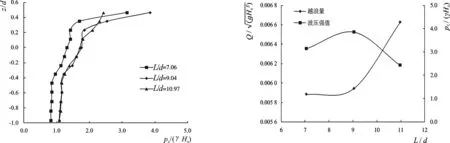
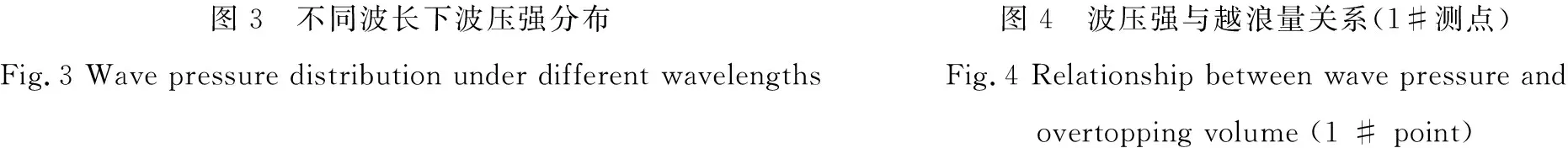
图3 不同波长下波压强分布Fig.3 Wave pressure distribution under different wavelengths图4 波压强与越浪量关系(1#测点)Fig.4 Relationship between wave pressure and overtopping volume (1 # point)

2.3 水深对波压强的影响

海港水文规范[12]曾根据直立堤基床形式、堤前水深、波高、周期等条件将堤前波浪分为立波、近破波、远破波三种形态，其中堤前水深对决定直立式建筑物的波态最为重要。本次试验在波高Hs=7.9 cm时分别对不同的水深d= 11.6、12.9、20.9和26.4 cm进行试验，观察试验中各水深条件下堤前波浪形态可知，当水深d= 11.6、12.9 cm时，此时静水位在承台以下，堤前波浪大多出现远破波形态，而当水深d= 20.9、26.4 cm时，堤前波浪形态以立波为主，试验所得各测点波压强分布见图5。由图可知，当试验水深较小时，波浪以远破波的形态直接作用在板桩墙上，此时板桩墙上波压强值远大于水深较大时波浪形态为立波时的波压强值。板桩墙上波压强值随着相对高度z/d(此时的z以实际地面为原点)的增加而显著增大，在承台与板桩墙连接处为最大值，同时，板桩墙上波压力值随着承台底部的超高△h(△h为承台底部距静水位的距离)的减小而增大。图5-b给出了不同承台超高 △h/Hs下承台底部上托压强分布图，可以看出，当水深较大，承台底部超高△h为负时，波压强沿程分布几乎不变，可以视为均布压强进行处理。而水深较小，承台底部超高h为正时，波浪对承台底部的作用夹杂着空气显得十分复杂紊乱，波压强沿承台底部分布也变化较大，波压强在承台与板桩墙连接处的承台底部测点处出现最大值，且随着x/B的增加而减小。可以得出，当波浪在堤前发生远破波形态时，其对结构物的作用远比发生立波形态时大的多，因此对板桩墙和承台进行设计时，应特别关心低水位时的工况，并以此为设计时的控制工况。

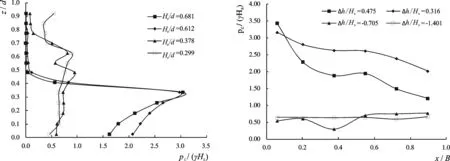
5-a 波压强高程方向分布5-b 波压强水平方向分布图5 不同试验水深下波压强分布Fig.5 Wave pressure distribution under different water depths

3 试验值与各家公式比较及经验公式

本次试验模型为实际因地制宜而设计的新型防波堤结构形式，在国内规范中尚未对该种结构提供设计参考依据，为进一步对该板桩承台式直立堤波压强进行分析与描述，拟结合类似现有研究较为成熟的直立墙前波压力理论公式与试验值进行比较，得出概括性的结论，为类似工程提供参考依据。

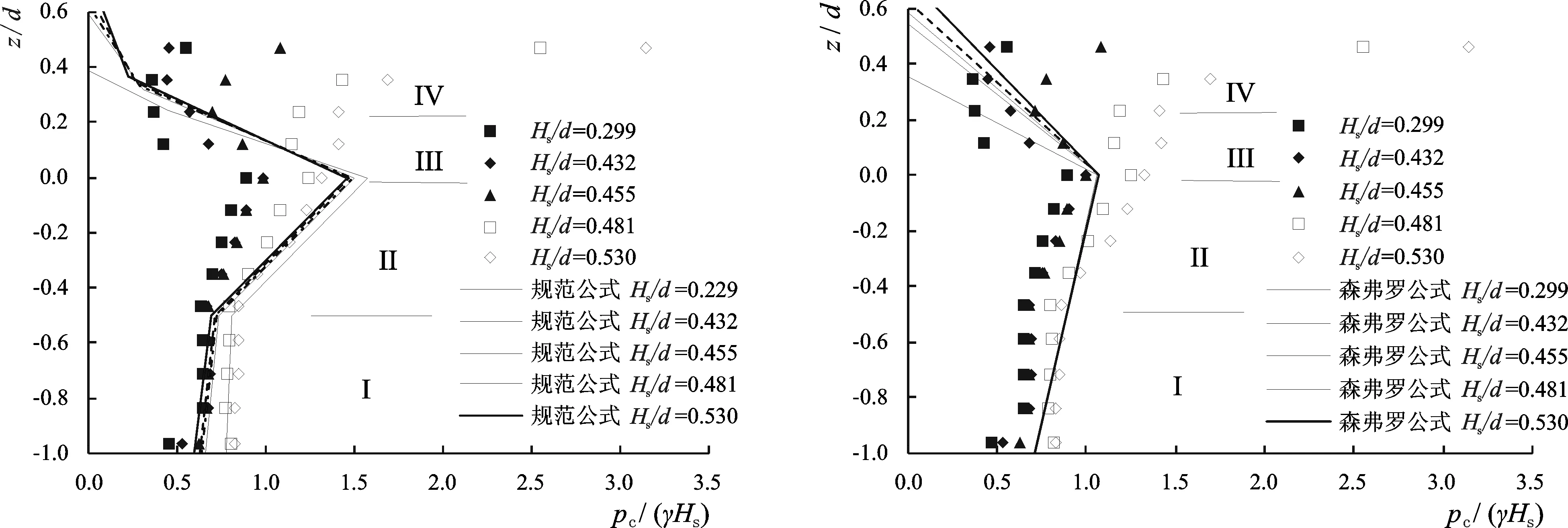
6-a 海港水文规范公式与试验值比较6-b 森弗罗公式与试验值比较图6 试验值与公式计算值比较Fig.6 Comparison of test values and formula calculation value

3.1 试验值与公式比较

由上述分析可知，当静水位低于承台时，波浪作用在承台上的浮托力明显增大，故为保证结构的稳定，设计时一般使得承台底部淹没在设计水位下一定距离。本次试验研究分别选用《海港水文规范2013》波压力立波计算公式[12](d≥1.8Hs且d/L=0.05～0.12)和森弗罗公式计算波压强值与试验值进行比较，对比结果详见图6。比较可知，对于静水位以下的第I、第II部分，森弗罗公式在第II部分与本次试验值相比明显偏小，而规范公式则均将试验值包含在内，波压强竖向分布规律与试验值相吻合。但这两类公式波压强计算值随相对波高的变化规律均与试验值相悖，原因在于这两类波压强计算公式均是以波浪在堤前成立波形态得出的，而本次试验虽以有效波高作为特征波高进行处理时满足立波条件，但当不规则波序列中的波高大于有效波高时，其波浪在堤前呈破碎形态，从而造成波浪相对压强值随相对波高的增大而增大。由图2-a中亦可以看出，试验相对压强值在相对波高Hs/d= 0.455到H/d= 0.481之间出现了较大的变化幅度，可以认为随着波高逐步变大，波序列中出现了较多的破碎波浪，从而使得相对波压强值明显变大。

3.2 经验公式修正与拟合

表1 波压强计算系数表Tab.1 The calculation coefficients of wave pressure

3.2.1 静水位以下部分公式修正

由3.1节的内容可知，海港水文规范公式(d≥1.8Hs且d/L=0.05～0.12)与试验值吻合度较高，但是由于破碎波的存在使得波浪相对压强随相对波高的变化规律有所不同，本节采用规范公式的波压强公式计算形式，对公式中的参数进行重新拟合，经多元非线性回归分析得静水位以下波压强计算公式如下，公式计算值与试验值比较见图7。

板桩墙或0.5倍水深以下按pbc均匀分布计算

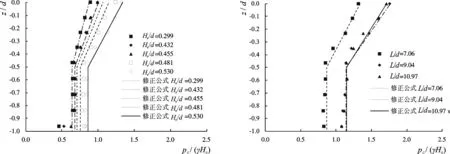
7-a 不同相对波高下7-b 不同相对波长下图7 试验值与修正公式计算值对比Fig.7 Comparison of test values and modified formula values

3.2.2 静水位以上部分公式拟合

对于静水位以上部分，由于挑檐的阻挡作用使得这部分的水体十分紊乱，不同位置处的波压强作用机理也不相同。对于挑檐与挡浪墙直立部分连接处的1#测点，当波高与堤顶超高比值较大时，波浪因结构阻挡而产生的向上水体直接撞击在该处，造成该测点的波压强值突增，因而在分析时应对此部位与其他部位分别考虑。

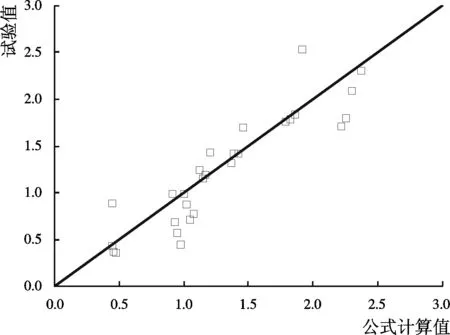
图8 静水位以上波压强公式计算值与试验值对比Fig.8 Comparison of test values and formula values above the still water level

基于以上分析，对于挑檐与挡浪墙直立部分连接处受到波浪水体直接撞击的部分，宜认为其波压强值约为2～4倍静水位处波压强值。同时考虑到当波浪波长足够大时，挑檐的作用影响甚微，但基于本次试验数据限制，本次公式拟合将不考虑波长足够大的情况，将其视作安全储备。根据静水位以上其他部位实验数据，分析规律确定函数形式并运用回归分析得静水位以上波压强计算公式如下

挑檐与挡浪墙直立部分连接处：pc=(2～4)poc

式中:Rc为堤顶高程至静水位处超高；B为挑檐的宽度。

公式适用范围：0.2≤Hs/d≤0.55，0.4≤Hs/Rc≤0.9，d/L=0.05～0.15

公式计算值与试验值比较见图8，试验值与计算值相关系数为0.90，公式与试验结果吻合度较高。

4 结论

(1)足够水深时，板桩承台式直立堤结构波压强在竖向分布上主要分为四个部分，静水位以上波压强值受挑檐的影响随相对高度增大而增大，承台底部波压强分布近似均匀分布。

(2)在不同波高与周期作用下，相对波压强值随波高的增大而增大，当波高增大到一定程度导致破碎波浪的出现时，相对波压强值将出现突增；相对波压强值随波长的增大而增大，但当波长足够大时，由于波浪越浪形态发生变化，波浪直接越过堤顶，挑檐对波浪水体影响较小，反而出现挑檐附近相对波压强值的减小。

(3)当静水位低于承台底部时，波浪以远破波的形态直接作用于板桩墙和承台底部，此时波压强值将显著增大，在结构设计时应对此种工况予以特别重视。

(4)本文拟合修正公式与试验值吻合较好，可供类似工程参考借鉴。