基于障碍期权的比例担保的定价研究

王祥宇，吴建华

（1.山东财经大学金融学院，济南 250200；2.济南大学数学科学学院，济南 250022）

引言

中小企业的发展面临的最大问题就是融资问题，从银行的角度考虑，对中小企业的贷款不仅管理成本高而且风险也很大，这就造成中小企业从银行等金融中介机构融资的困难，导致企业的经营处于停滞状态，甚至破产。造成银行对中小企业实行信贷配给[1]的主要原因就是小企业和银行之间的信息不对称。因此，解决中小企业融资难题的根本思路应该是减少信息不对称对贷款融资的负面影响，提高中小企业与银行之间的信息传递，其中途径之一就是发挥第三方担保机构的作用，对中小企业给予融资信用担保，在企业与银行之间搭建桥梁，从而实现中小企业顺畅的间接融资。事实上，这也是中小企业信用担保机构产生的根本原因。

但是，在我国目前的中小企业信用担保实践中，贷款信用担保并没有很好地解决中小企业的融资问题。我国信用担保业起步较晚，加上金融体制改革不到位和监管错位，导致我国中小企业担保业发展一直落后于实践的需要，特别是在担保风险的控制与防范方面比较落后。另外，在我国目前的银行业还处在相对强势的地位，大都采用全额担保的形式，其中担保机构承担几乎大部分贷款的连带清偿责任，这将容易造成“道德风险”，也就是降低了对贷前的企业经营状况的调查和资信审查的标准，导致担保公司承担了很多高风险担保。同时，在签订担保合同后，银行对企业的事后监督的积极性和力度也降低。这种不对等的经济地位，也迫使中小企业担保行业畸形发展，有些甚至变为放高利贷者，极大地扭曲了本来意义上的担保机制。

从国外信用担保运作的经验来看，建立风险分担机制，由担保机构承担大部分风险，银行承担少部分风险，既可以防范金融机构的道德风险，强化其对贷款企业的责任感，又有利于加强银保之间的合作。比例担保作为一种商业银行与担保机构风险共担、利益共享的机制，应该得到银行及担保机构的重视。比例担保的核心问题就是，担保比例的确定，即担保的定价问题。本文首先简要回顾了信用担保定价的国内外研究现状，分析了比例担保与向下敲出的欧式看跌障碍期权的同构性，然后基于期权定价的保险精算思路给出了比例担保理论担保费的定价模型，并且对模型的应用进行了分析，最后总结全文并给出进一步研究的思路。

一、信用担保定价的国内外研究述评

自Samuelson在1969年提出担保定价以来，国外的学者和专家开始了对信用担保定价方面的研究。Merton（1974）首次提出信用担保的期权特性，认为担保合约实际上是一份看跌期权，该看跌期权的标的物为债务方企业的净资产，所以在一系列强假设条件下可以使用Black-Scholes期权定价模型对信用担保进行定价[2]。Jones et al（1980）首次探讨了不可赎回零息债券的全额担保、部分担保，优次级不可赎回零息的全额担保、以及可赎回零息债券担保的定价问题[3]。Lai（1994）在考虑利率的随机性基础上，使用数值模拟对可违约贷款担保各变量做了比较静态分析[4]。Gendron et al（2002）从组合担保风险分散，债务担保能力及担保期限角度分析了贷款担保组合的风险管理问题[5]。Jun，Jae Bum（2008）在 B-S 期权定价模型的基础上，提出了针对实物期权的二项式模型，给出在BOT项目中政府担保的定价方法，并用相关实际项目对模型进行了适用性检验[6]。

我国信用担保起步较晚，我国经济学界对信用担保定价的理论研究涉足较少，但是从目前来看，信用担保定价已经引起了国内众多学者和专家的广泛关注。林昆辉等（2000）从理论和实证两方面论述了如何运用Blake-Scholes的期权定价模型确定担保收费的问题[7]。陈富权等（2004）在Black-Scholes期权定价理论的基础上，提出了信用担保的两阶段定价模型[8]。徐友传、何佳（2007）在考虑最低净现金流与担保定价关系的基础上，给出了在最低净现金流要求条件下的信用担保定价方法[9]。陈晓红等（2007）基于债务展期,研究了担保定价问题[10]。顾海峰（2007）在展期阶段可选的情况下,研究了存在多个债务展期情况下的担保价值及其影响因素[11]。钟田丽等（2008）通过相对VaR的方法，研究了既考虑企业原有债务，又考虑企业对于担保方的展期债务的两期担保定价模型[12]。徐云（2015）还针对服从布朗运动的标的资产价格，采用拟鞅定价方法对信用担保进行定价研究[13]。

以上文献中的担保定价，大多数是基于全额担保的条件下，通过改变利率的随机性，信用风险的度量的方式，担保期限的延伸，以及组合形式下的担保的定价问题和实证分析思路。关于非全额担保的研究相对较少，近期比较有代表性的是熊熊等（2011）[14]运用博弈论对银行、企业、担保机构三方的合作过程进行分析，研究发现，比例担保是比全额担保更为有利的选择，在实际操作中担保机构应承担较大的比例。但是，该文只是强调了比例担保的优越性，仅仅引用了美国、英国、法国、德国和加拿大几个国家采用的担保比例，但并没有给出如何得到这些担保比例，而且没有给出在该比例下的应当收取的担保费率的大小。本文的研究重点就是利用期权与担保的同构性，推演出比例担保与向下敲出欧式看跌期权的同构性，并且给出了比例担保下的担保费率的确定。

二、比例担保与欧式障碍期权的同构性

所谓比例担保，就是担保机构只对担保贷款的一定比例负责，超出比例的部分由银行承担。下面给出比例担保运行机制的数理模型。

设担保机构对企业的贷款L进行信用担保，担保额为M（0＜M＜L），担保比例为 δ=M/L（0＜δ＜1），具体运行机制如下：

1.当企业资产价值VT大于到期债务值DT的时候，即所有者权益ST＞0，企业能够按期偿还贷款本息，保留企业控制权继续经营，此时无须担保，担保的内在价值为0；银行收回全部的贷款本息，即银行收益CT=D。

2.当企业资产价值VT小于或等于到期债务值DT的时候，即所有者权益ST≤0，企业不能足额偿还贷款本息。首先，如果-Lδ＜ST≤0，企业处于“休克状态”，担保机构支付担保额-ST之后，剩余部分债务（D+ST）企业仍然有能力偿还，此时企业保留企业控制权。担保的内在价值为-ST=D-VT，银行收益CT=D。其次，如果 ST≤-Lδ，企业处于“濒死状态”，担保机构支付担保额Lδ，但是剩余部分债务（D-Lδ）企业没有能力偿还，此时企业将企业控制权移交给银行。担保的内在价值为Lδ；银行只能够收回部分的贷款本息Lδ，但是获得了企业资产的控制权，可以通过破产清算进一步的降低损失，即银行收益CT=Lδ+VT。因此，比例担保在T时刻的内在价值为：

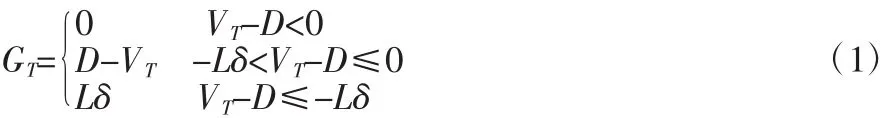
显然，此时的比例担保可以看成是一个标的资产为VT、执行价格为D、障碍价格为B=D-Lδ、到期日为T的向下敲出欧式看跌期权，该障碍期权在t时刻期权的价格C（Vt，t）。那么，C（V0，0）就是我们要求的比例担保的担保费。

三、比例担保理论保费确定的精算模型

下面将根据比例担保与欧式障碍期权的同构关系，利用期权定价的保险精算思路给出计算比例担保的理论保费的方法。

1.基于保险精算方法的期权定价原理。保险精算定价方法最早由Bladt和Rydberg于1998年提出，并且可用于期权定价。利用期望均衡原理确定的期权费就是相应收益（损失）的期望值。以欧式看涨期权为例，标的资产的价格可认为是到期日标的资产可能发生的损失ST，双方互相约定的执行价格则相当于免赔额X，假定初始时刻为t，保险到期日为T，t∈[0，T]，则到期日 T 保险人的损失为 max（ST-X，0），如果以CT表示在T时刻期权价值，则在到期日T，保险费（期权费）的价值为：

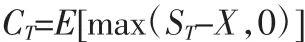
由于收到（支付）保险费（期权费）发生在现在，未来在期权到期日才会支付（收到）保险费（期权费）的偿付，因此需要对保险费（期权费）的期望损失（收益）贴现。在初始时刻t收到（支付）的保险费（期权费）Ct由下式给出，即：

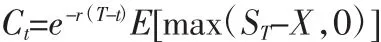
2.基于保险精算定价方法的障碍期权定价模型。首先给出向下敲出欧式看跌期权的运行机制（如图1所示）。

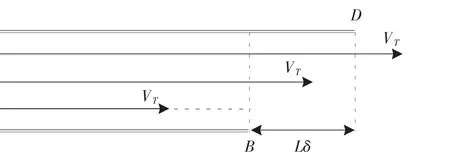
图1 向下敲出的欧式看跌期权运行机制

下面给出该障碍期权的到期现金流（期权到期价值），以公式表示如下：

由期望均衡原理可知，考虑在条件为风险中性的情况下，在t时刻期权的价格可按照其到期现金流量的期望值以无风险利率r折现到时刻t，其表达式为：

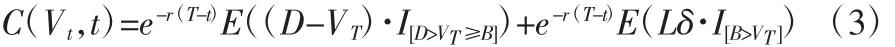
式（3）中的I为示性函数。式（3）则是基于保险精算方法的一个障碍期权定价模型，其实质是一个最高赔付上限为Lδ且具有现金补偿的向下敲出看跌期权定价模型。

设企业的价值为VT，利用Black-Scholes期权定价模型的基本假设，可假定VT服从几何布朗运动：

其中μ，σ＞0为常数，μ为企业价值的期望瞬间报酬率，σ是资产报酬率的瞬间标准差，Wt为标准Brown运动，满足式（4）方程的解可称作几何Brown运动。利用Ito^公式可得：

即 lnVt，t∈[0，T]是一个服从漂移率是常数 μ，波动率是σ2的几何 Brown 运动。当 t＞0 时，式（5）等价于 lnVt～，即VT服从对数正态分布。在风险为中性的情况下，期望收益率μ=r。如果给定t时刻企业的价值Vt，那么在T时刻，企业资产的价值VT的条件分布就是以均值、方差Var[lnVT|Vt]=σ2（T-t）的对数正态分布。则在给定给定Vt的情况下，VT的条件概率密度函数记为：

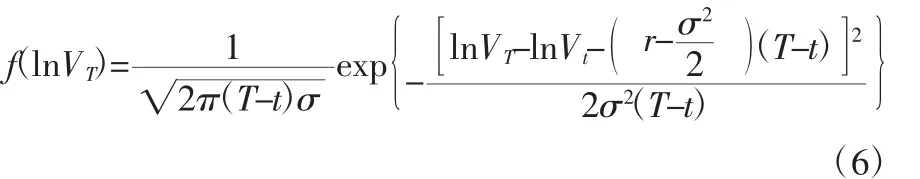
将式（6）代入式（3），该期权价格可表示为：

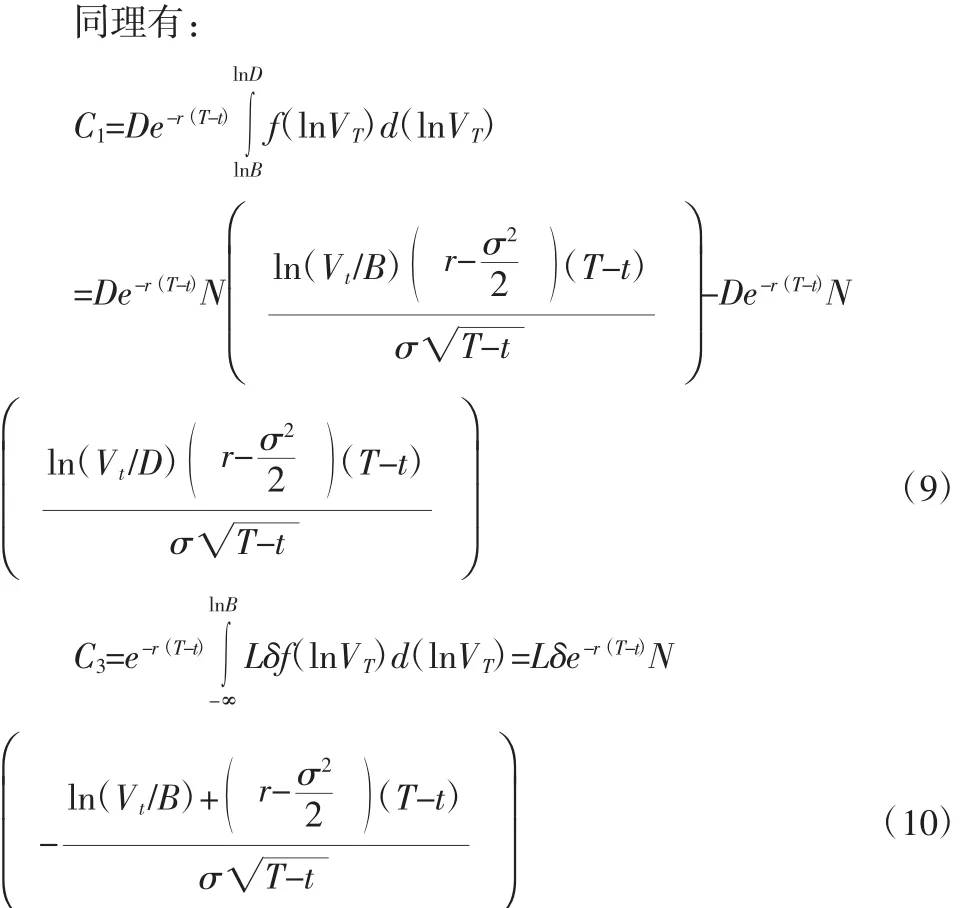
由式（7）、式（8）、式（9）和式（10）可以得到企业价值 VT的障碍期权定价模型为：

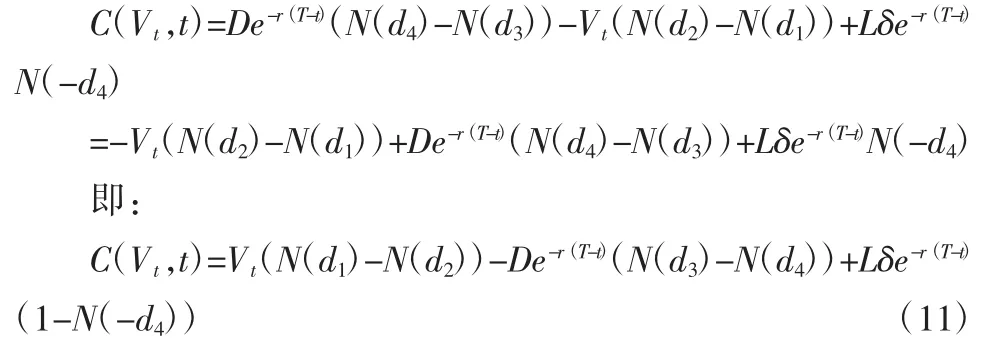
式中，N（·）为标准正态分布累积分布函数。

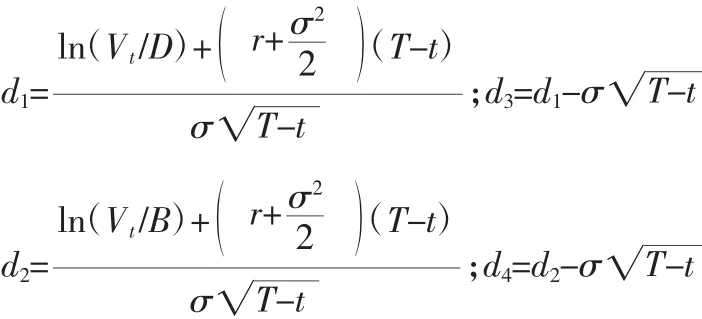
若令δ→1，即相当于不设障碍价格，没有最高赔付上限，则可推出基于Black-Scholes公式的企业价值VT的欧式看跌期权定价模型为：

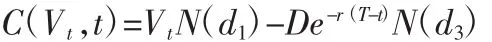
式中，N（·）为标准正态分布累积分布函数。

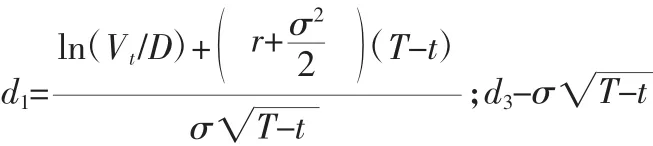
那么，由式（11）可得，在担保合同签署的时刻0，企业需要向担保机构缴纳的担保费就是C（V0，0），公式如下：

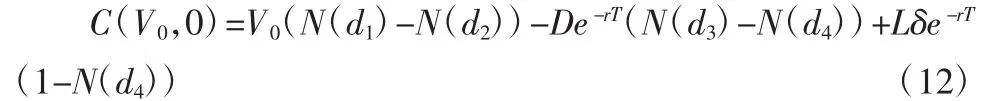
式中，N（·）为标准正态分布累积分布函数。

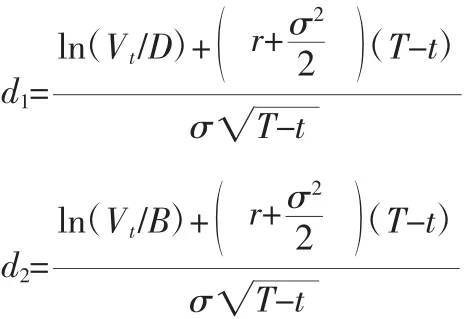
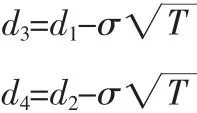
四、模型的比较静态分析

从上面第四部分推导出的担保费C（V0，0）可以看出，影响担保费的因素有多个。为了深入了解担保合约价值的影响因素以及影响程度，下面给出担保价值影响因素的敏感性分析（如图2所示）。

从图2可以看出，贷款担保价值随着企业的初始总资产价值V0，担保比例δ=M/L和无风险利率r的增大而减少。贷款企业资产初值越大，其违约的可能性越小，担保方代偿的可能性减小，从而担保价值减少；担保比例越大合约被敲出的可能性变大，而到期补偿的现金流也减少，由于敲出可能性变大引起担保价值增加的作用超过了由于敲出时补偿现金流减小引起担保价值减小的作用，因而担保价值减小；而无风险利率是折现利率，它的增大代表担保价值现值减小。从图2中也可以看出，其中贷款企业资产初值对担保价值的影响最为敏感，是担保方控制风险的重要因素。另外，从图2还可以看出，随着担保比例的增加，担保价值加速下降，敏感性变大；随着贷款企业资产增加，担保价值减速下降，敏感性变小；而对于无风险利率，减小速度基本平缓，敏感性基本不变。从这个角度来看，虽然担保价值对贷款企业的资产初值的敏感性最大，但是担保比例得敏感性变化速度最快，当变化幅度大过一定程度时，担保比例的敏感程度会超过资产初值的敏感性。以上分析表明，资产初值和担保比例都是担保方控制风险的重要因素。

五、模型的应用分析

本文所研究的中小企业没有发行股票和债券的资格，企业的资产仅由所有者权益S和银行贷款L两部分构成。企业的负债全部为银行贷款。假设企业在0时刻获得贷款本金是L，贷款期限是T，贷款利率为R，那么，在贷款的初始0时刻，企业的资产价值V0=L+S0。此时，企业的资产负债率为λ=L/V0。在贷款到期T时刻，企业的总资产VT就等于贷款到期值D=L·R与到期所有权益价值ST之和，即VT=D+ST。我们给出约束性担保额上限为M（≥0）。

1.担保费 C（V0，0）的决定因素。根据我们得到的担保费的定价模型（12），可以看出影响担保费高低的因素主要有以下6个：企业的总资产价值V0，无风险利率r，贷款到期值D，贷款期限T，约束性担保额上限为M（0＜M≤L），企业资产价值的波动率为σ2。下面我们通过一个定价实例来实现模型的定价。（1）企业的总资产价值V0。被担保企业的初始总资产价值，可以用利润或者销售额来估算，这可以通过查阅审核企业的财务报表得到较为准确的数值，不妨假定某公司的初始总资产价值为500万元。（2）无风险利率r。无风险利率r可以参考我国的货币市场基准利率——上海银行间同业拆借利率（Shibor），不妨假定r=5%。（3）贷款到期值D和贷款期限T。贷款到期值D和贷款期限T一般由企业和银行协商确定。这里不妨假定贷款的到期值的账面金额为250万元，贷款期限为五年。（4）约束性担保额上限为M。担保额上限M可以由担保机构和银行根据相关的担保法律法规协商确定，并且有B=D-M。不妨假定M为150万元，B=100万元。（5）企业资产价值的波动率为σ2。显然，只有企业资产价值的波动率为σ2是一个未知的变量，这个变量代表企业的资产贬值而产生的信用违约风险。下面我们进行对σ2进行估算，我们可以通过企业的利润或销售额的年复波动率来估算公司价值的年复波动率。

2.企业资产价值的波动率σ2的估算以及担保费率的计算。首先在固定的时间间隔ΔT选取相应的公司价值，并将其记作为：Tk=T0+k·ΔT（k=1，2，…，n），其中 ΔT 以年为单位。Tk对应的公司价值为S（kk=1，2，…，n），因为 σ 是公司价值年复波动率的标准差，于是可设：Ek=ln（Sk/Sk-1），显然变量 Ek的标准差为，根据统计学相关理论，变量Ek的无偏统计量是的最优估计，根据无偏统计量的定义，则可得σ的最优估计式：

我们借用顾海峰[15]在2009年所采用的数据，首先给出此公司每个月（共18个月）的利润假设表（如下表所示）来确定，显然有，以此刻测算企业资产的年复波动率σ。

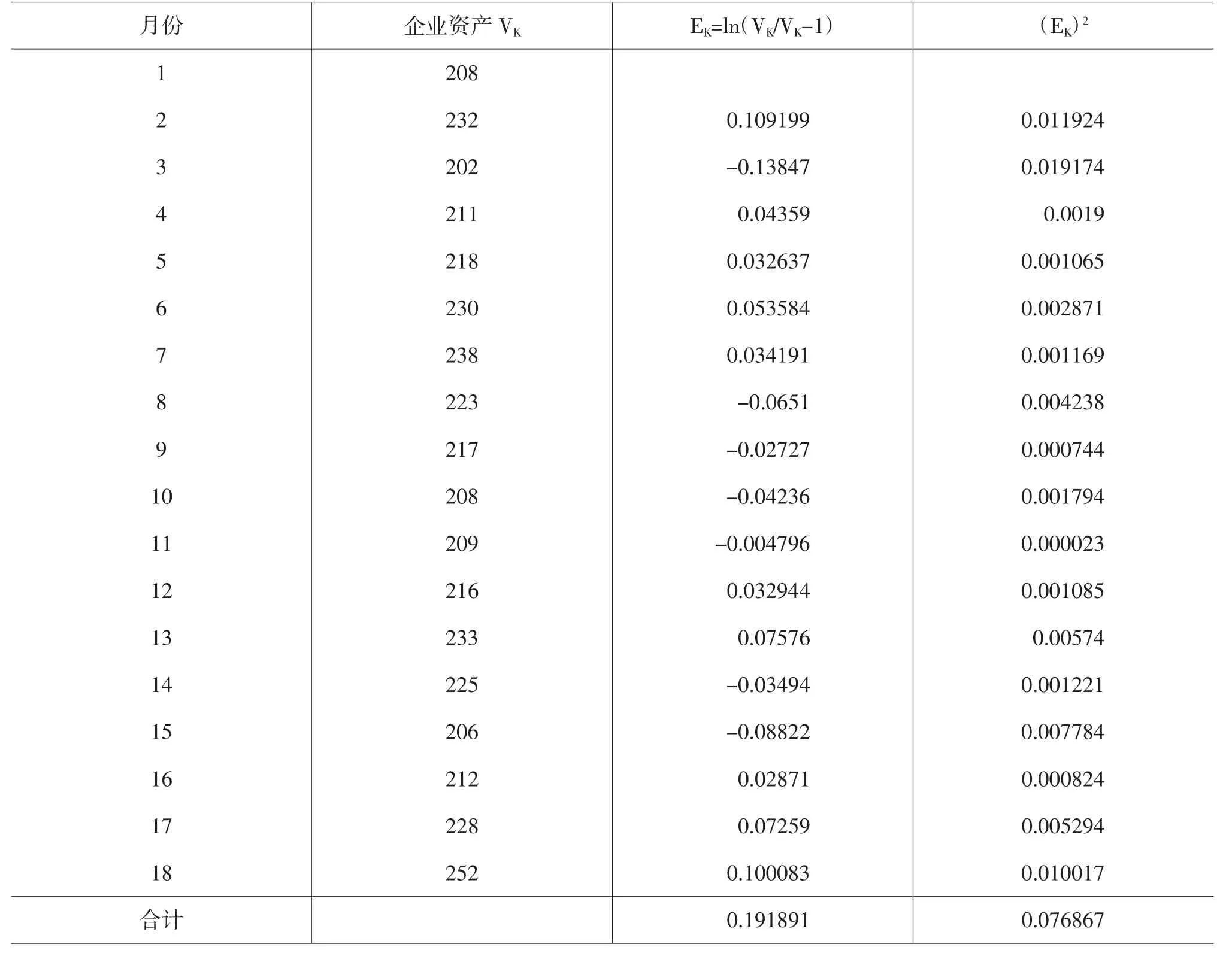
公司每个月的利润 单位：万元

下面我们对照定价公式（12）进行分析，已知V0=500，D=200，r=5%，T=5，σ=22.98%。把上述数值代入定价公式（12），则有：

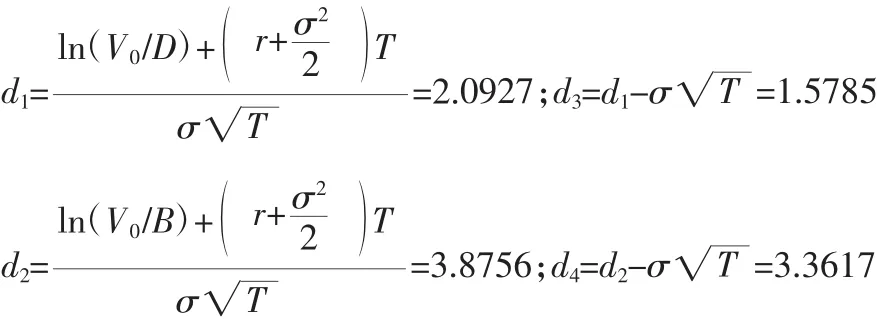
通过查标准正态分布表，有 N（d1）=0.9818，N（d3）=0.9428，N（d2）=0.9999，N（d4）=0.9996。因此，在担保合同签署的时刻0，企业需要向担保机构缴纳的担保费就是C（500，0），公式如下：

六、结论和下一步的研究方向

比例担保可以合理降低担保机构的风险，本文基于比例担保与欧式障碍期权的同构性，利用保险精算思路给出了比例担保的理论保费，即：

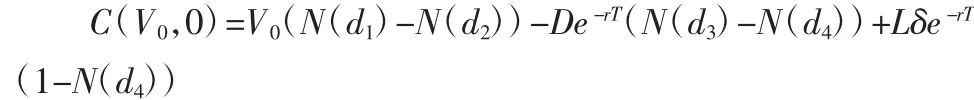
其中，无风险利率r可以参考我国的货币市场基准利率——上海银行间同业拆借利率（Shibor）；贷款到期本息D，贷款期限T由企业和银行协商确定；企业的总资产价值V0可以通过查阅审核企业的财务报表得到较为准确的数值；担保机构承担的比例δ可以由担保机构和银行根据相关的担保法律法规协商确定；只有企业资产的波动率为σ2是一个未知的变量，这个变量代表企业的资产贬值而产生的信用违约风险，可以利用已有的信用违约风险理论进行估算。

对该理论保费进行了敏感性分析，发现企业资产初值对担保价值的影响最为敏感，是担保方控制风险的重要因素。另外，随着担保比例的增加，担保价值加速下降，敏感性变大；随着贷款企业资产增加，担保价值减速下降，敏感性变小；而对于无风险利率，减小速度基本平缓，敏感性基本不变。从这个角度来看，虽然担保价值对贷款企业的资产初值的敏感性最大，但是担保比例得敏感性变化速度最快。当变化幅度大过一定程度时，担保比例的敏感程度会超过资产初值的敏感性。这些分析表明，资产初值和担保比例都是担保方控制风险的重要因素。