基于悬架非线性特性的稳定杆连杆建模方法研究∗
2018-07-24李小珊韦宝侣秦再武李德淯
李小珊,韦宝侣,张 庆,秦再武,纪 浩,李德淯
(上汽通用五菱汽车股份有限公司技术中心,柳州 545007)
前言
由汽车转向产生的侧倾力矩将引起内侧向外侧车轮的载荷转移,产生车身侧倾,此时,安装在悬架系统上的横向稳定杆组件可提供一个绕侧倾轴线的回位力矩,即提高侧倾角刚度,减小车身倾斜[1-2]。稳定杆组件由横向稳定杆、稳定杆连杆、稳定杆衬套和夹箍组成,对整车侧向稳定性有重要影响。
稳定杆系统中对稳定杆连杆的建模分析,国内相关文献资料较少。稳定杆连杆在工作中主要承受两端球铰的压缩载荷,属于典型的两端铰支压杆,传统的强度校核方法有两种:通过失稳理论[3]公式或台架试验方法获得其临界载荷。而实际中稳定杆连杆并非理想压杆,与边界条件简化的失稳理论公式和压杆台架试验获取的临界载荷都有较大的误差。文献[4]中通过约束稳定杆连杆一端所有自由度,另一端加载启动力矩进行疲劳分析,发现稳定杆连杆头部断裂原因为球铰启动力矩过大所致;这是传统台架试验方法,文献未进一步叙述与实际情况的差异。文献[5]中进一步关注了实际工况的稳定杆连杆载荷情况:通过采集试验场工况中稳定杆连杆的最大应变,反算出稳定杆连杆的最大受力值。
汽车悬架的非线性因素一般集中在悬架弹簧、阻尼、橡胶衬套和轮胎上,在进行悬架系统建模和动态特性分析时,其非线性特性对分析结果影响十分突出,不容忽视[6-7]。本文中以某轿车悬架为研究对象,建立了基于Abaqus软件平台的悬架非线性特性的多体系统有限元模型,通过路谱采集获取载荷作为输入,进行稳定杆连杆的强度分析,并对比失稳理论和台架试验获取的临界载荷结果,对该建模方法进行评价。
1 3种临界载荷获取方法
3种临界载荷获取方法分别为:(1)压杆失稳理论计算;(2)压杆台架试验测试;(3)悬架多体系统模型求解。其中稳定杆连杆为典型的两端铰支压杆,根据压杆失稳理论[3]直接求解临界载荷和临界应力。
1.1 压杆台架试验
稳定杆连杆两端球铰中心点连线并非完全与连杆中心线重合,即作用在连杆上的轴向压力不可能与轴线完全重合,且载荷不会完全没有弯曲,在台架试验中发现轴向压力尚未到达失稳条件的临界载荷,压杆已达到屈服状态。
根据压杆失稳特性,可设计专用夹具在万能拉压试验台上测试出稳定杆连杆的失稳临界载荷,如图1所示。稳定杆连杆装夹固定方式模拟整车上的装配方式,两端用紧固件紧固在刚度足够大的万能拉压试验台上,沿轴向以10mm/min的速度加载,直至压杆屈服后,记录屈服点的临界载荷。

图1 稳定杆连杆试验台架
1.2 悬架多体系统模型的载荷提取与验证
1.2.1 悬架多体系统有限元模型的建立
研究车型前悬架为麦弗逊悬架,单侧悬架的零部件与运动拓扑关系如图2所示,连接副为Abaqus的连接属性。其中转向节与减振器筒、减振器活塞杆与Top-mount、转向齿条与转向机壳体、转向机壳体与副车架之间为Beam固定连接;转向节与下控制臂、减振器筒与稳定杆连杆、稳定杆连杆与稳定杆、转向节与转向拉杆、转向拉杆与转向齿条之间为球铰Joint连接;Topmount、横向稳定杆、下控制臂与副车架/车身均为衬套Bushing连接,Bushing连接中设置衬套6个方向的非线性刚度;减振器筒与活塞杆通过圆柱副Cylindrical连接,Cylindrical连接中设置缓冲块非线性刚度,并加入考虑弹簧刚度及长度特性的Axial连接副。
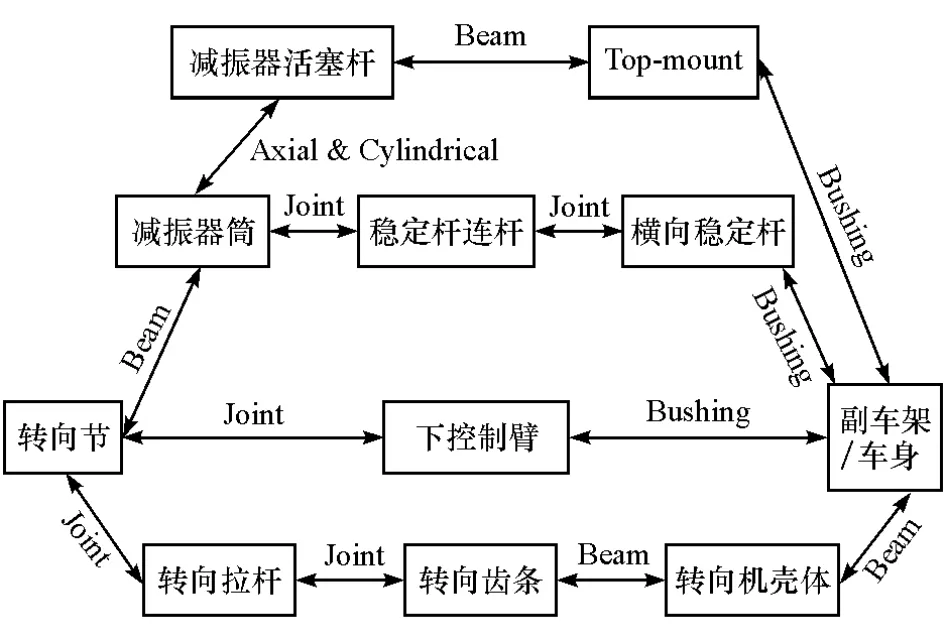
图2 麦弗逊悬架运动拓扑关系(单侧)
基于麦弗逊悬架的拓扑结构,在Abaqus中建立完整的悬架多体系统模型,并将稳定杆连杆、横向稳定杆、稳定杆夹箍的网格模型导入,分析步中考虑几何大变形的非线性求解,最终建立的稳定杆连杆有限元模型如图3所示,悬架模型中非线性参数设置见表1。
图3 基于悬架多体系统的有限元模型
1.2.2 载荷提取与验证
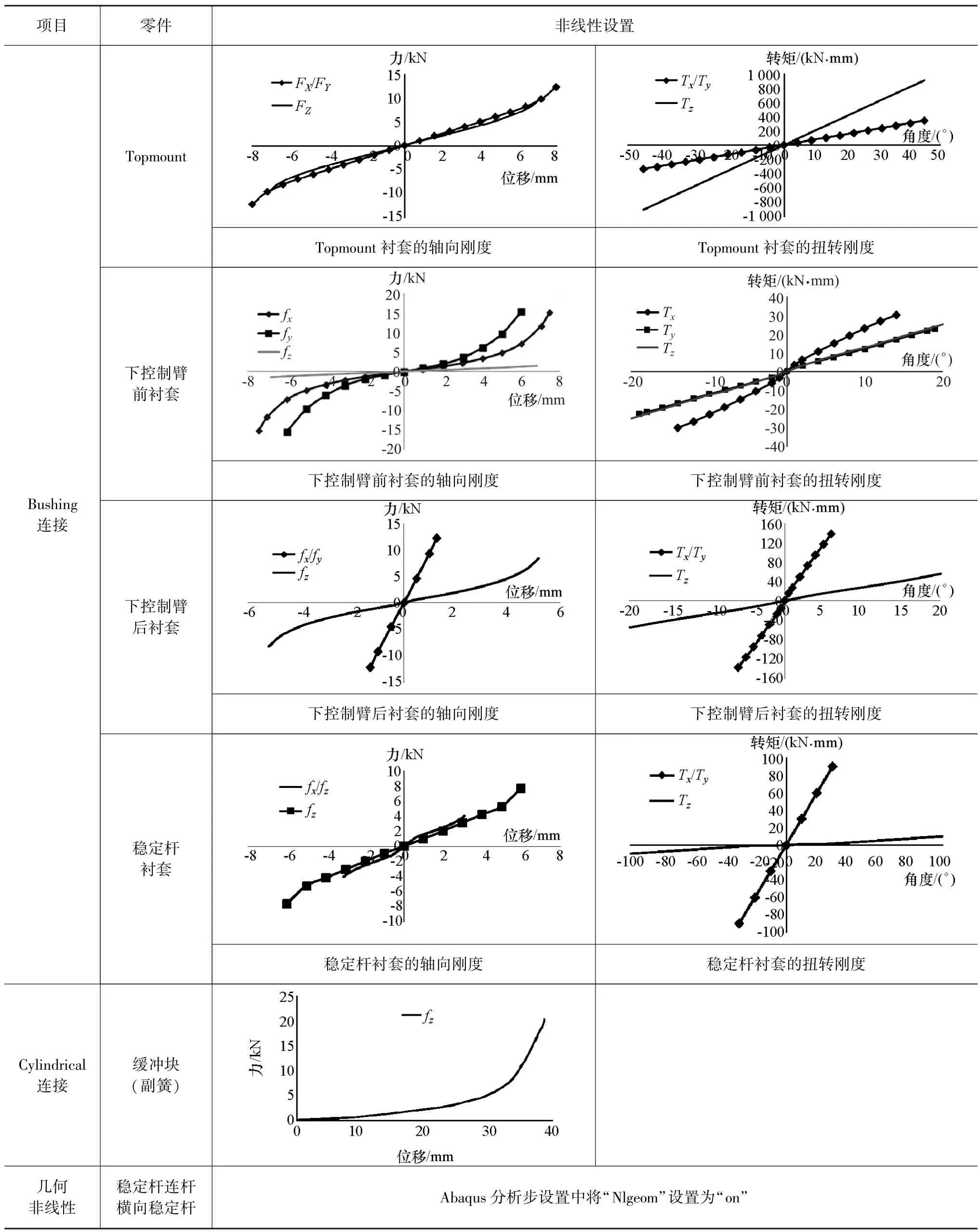
表1 悬架模型的非线性参数
从悬架多体系统可提取任意输入工况下对应的硬点载荷。根据稳定杆连杆的运动和受力特性,其最大载荷工况必然发生在反向轮跳量最大的工况。因此,只要确定了车辆实际行驶过程中的最大反向轮跳量,即可从仿真模型中获得该工况下的最大载荷;并求解出稳定杆连杆有限元模型的最大应力;再根据所使用的材料强度特性,反求该车型该工况下处于临界应力时的稳定杆连杆直径。
本文中通过标定的方法获得稳定杆连杆应变与受力[5]和悬架弹簧应变与车辆轮跳的关系,然后在整车试验场进行应变测试最终获取稳定杆连杆的最大载荷及该载荷下对应的汽车轮跳参数。
根据稳定杆连杆和悬架弹簧的受力特点,应变片贴片方案如图4所示,稳定杆连杆采用消除弯曲影响的全桥电路见图4(a),悬架弹簧采用测量扭转切应变的半桥邻臂电路见图4(b)[8]。

图4 应变测试试验方案
稳定杆连杆的待测应变ε包括轴向拉压应变εP和弯曲应变 εM,即

式中μ 为材料泊松比。 又有:εP=εP1=εP3,εM=εM1=-εM3,因此稳定杆连杆测试方案仅有拉压应变,桥路输出应力值为
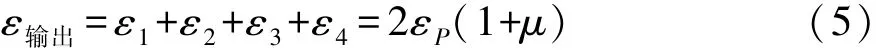
悬架弹簧随悬架行程变化时主要承受剪切作用,应变片相互垂直,故有 ε=ε1=-ε2,即

2 某车型的稳定杆连杆强度分析
某车型稳定杆连杆的示意图如图5所示,杆长300mm,杆径10mm,材料为20#钢,材料屈服强度≥245MPa。分别使用失稳理论、台架试验和悬架多体系统有限元分析3种校核方法进行强度校核。
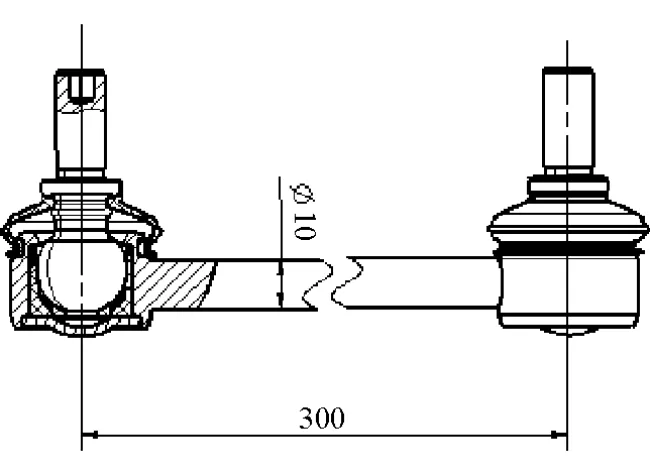
图5 稳定杆连杆
2.1 路谱载荷采集
采集整车道路试验中极限工况下分析车型的稳定杆连杆极限载荷,以进行3种方法获取的临界载荷进行判断。为方便下一步有限元模型的载荷输入,进行稳定杆连杆载荷谱测试时,同步测试对应前悬架的轮跳量。
首先标定测试车辆的稳定杆连杆应变与受力、悬架弹簧应变和车辆轮跳的线性方程。然后在整车道路试验场采集这两个零件不同工况的应变数据,再将其代入标定获取的线性方程,最终得到稳定杆连杆载荷和对应的悬架轮跳。典型工况的测试数据如表2所示。由表可见,极限转向2工况的右侧稳定杆连杆载荷最大,此时压缩载荷为 Froad=1289.3N,对应轮跳为左轮跳 25.6mm,右轮跳-68.4mm。
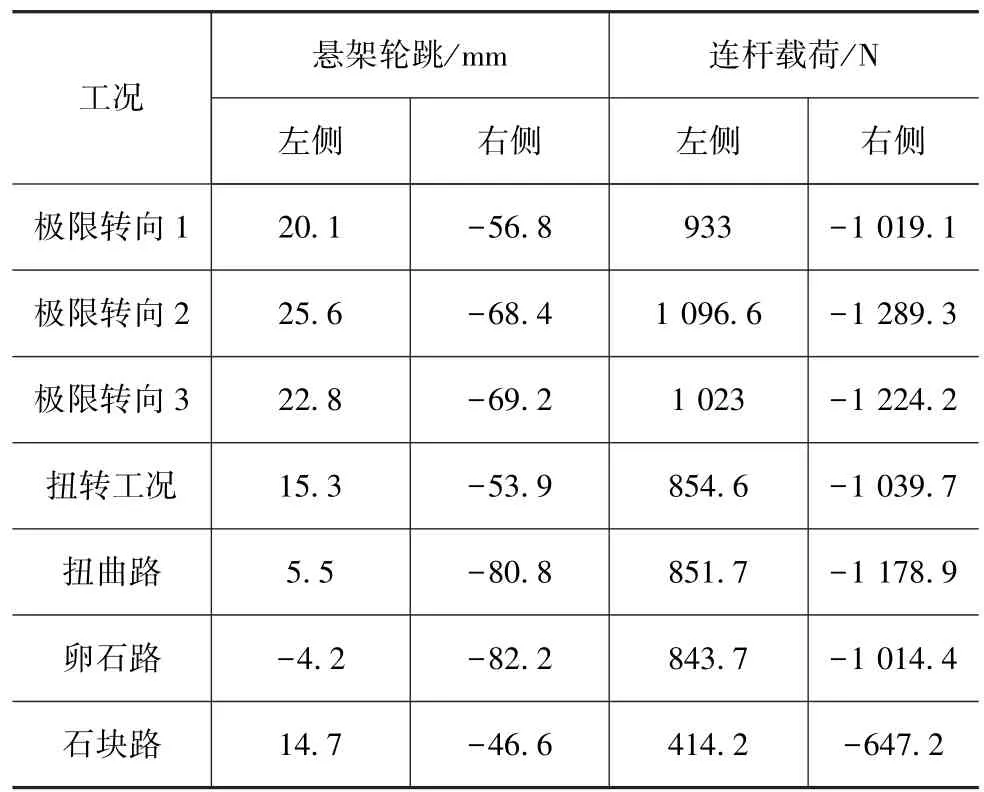
表2 同时刻下悬架轮跳量和连杆载荷
2.2 压杆失稳理论校核
该稳定杆连杆结构满足大柔度杆假设,求得失稳临界压力 Fcr=11070N,临界应力 σcr=141MPa。失稳临界压力Fcr远大于稳定杆连杆道路极限载荷Froad,连杆不会失稳。
2.3 压杆台架试验测试
选取20根该规格的稳定杆连杆进行图1所示的台架试验,当稳定杆连杆到达失稳状态后,记录加载力值,结果如表3所示,稳定杆连杆被压弯的临界载荷均值为Ftest=5880N,试验后连杆状态已永久变形,如图6所示。
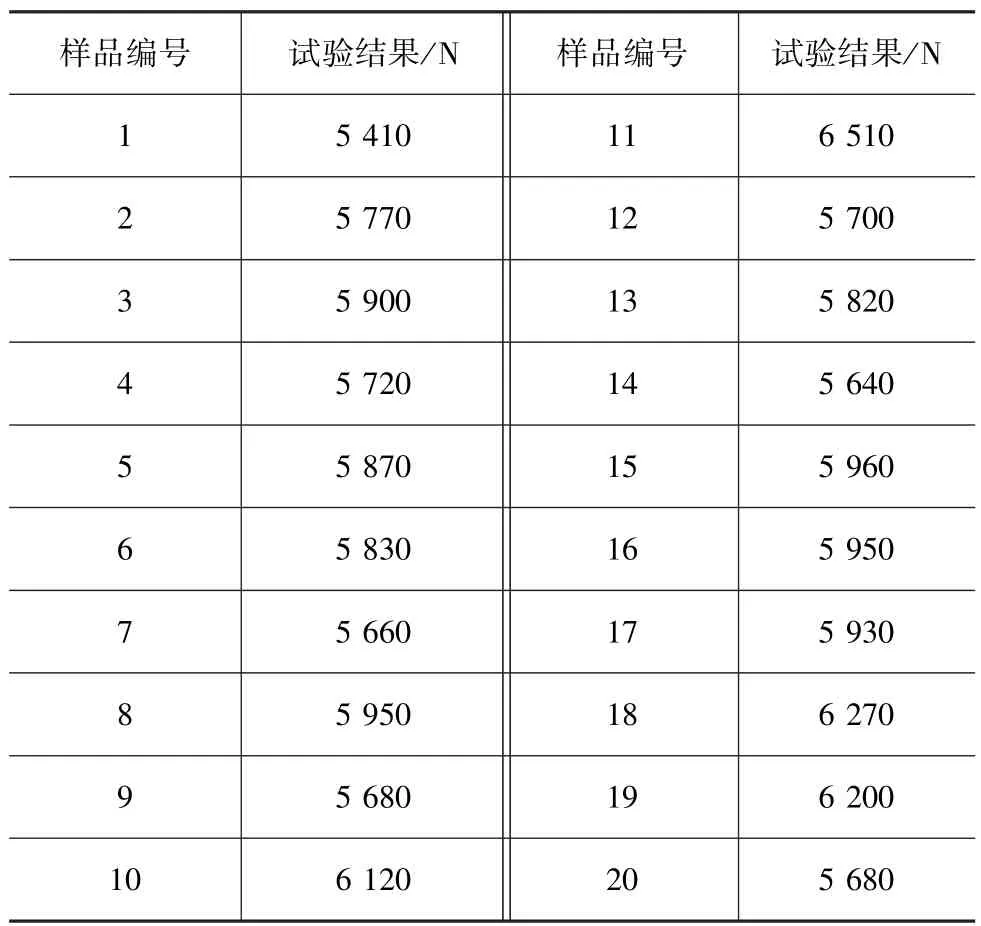
表3 压杆台架试验结果

图6 台架试验后的稳定杆连杆
台架试验临界载荷与道路极限载荷的比为Ftest/Froad=4.56,该连杆强度设计很安全。
2.4 有限元模型校核
将表2极限转向2工况的左上跳量25.6mm和右下跳量-68.4mm施加到已搭建好的该车型稳定杆连杆有限元模型的轮心上,提交求解器进行运算。求解完成后,提取左右稳定杆连杆上下球销点的沿连杆轴线(Z向)的载荷,见表4,其中正号表示沿轴向向上,反之,负号向下,即左稳定杆连杆为受拉,右连杆受压。由表4可见,轴向载荷仿真值与表2实测值非常吻合,精度达93.4%以上,CAE模型结果可表征实车稳定杆连杆载荷和应力情况。
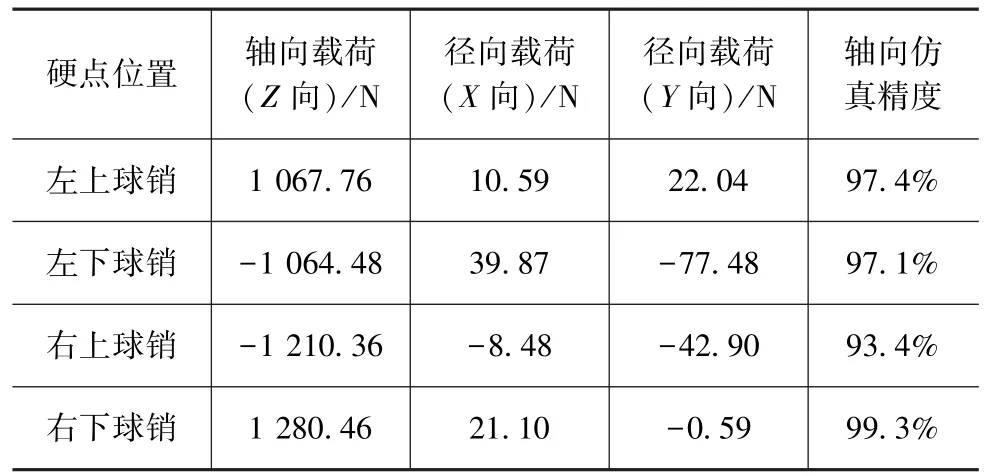
表4 工况极限转向2工况的硬点载荷
此时稳定杆连杆最大应力131.2MPa大于材料屈服σs,强度设计安全,如图7所示。
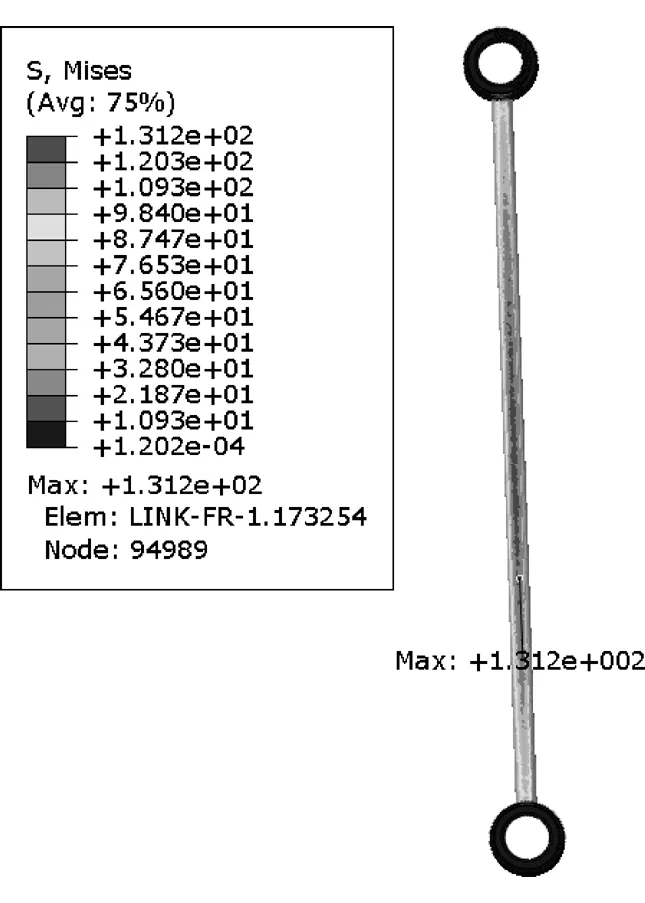
图7 稳定杆连杆应力云图
2.5 小结
通过以上对比分析,3种方法均可判断该车型的稳定杆连杆初始设计方案满足强度要求,但很难判断三者的优劣。
本文中进一步通过减小有限元模型中的连杆杆径,反求稳定杆连杆弯曲时的临界载荷,再与失稳理论和台架试验结果进行比较。
3 基于有限元求解的结果验证
3.1 有限元模型临界载荷求解
初始方案稳定杆连杆的杆径为10mm,最大应力为131.2MPa,通过减小杆径,反算其在相同轮跳下应力能达到材料屈服的杆径。
当杆径为8mm时,此时稳定杆连杆应力244.7MPa,接近材料临界屈服强度245MPa,如图8所示。左右稳定杆连杆硬点载荷见表5,提取右连杆上下球销载荷分别为-1 963.75和1 963.32N。
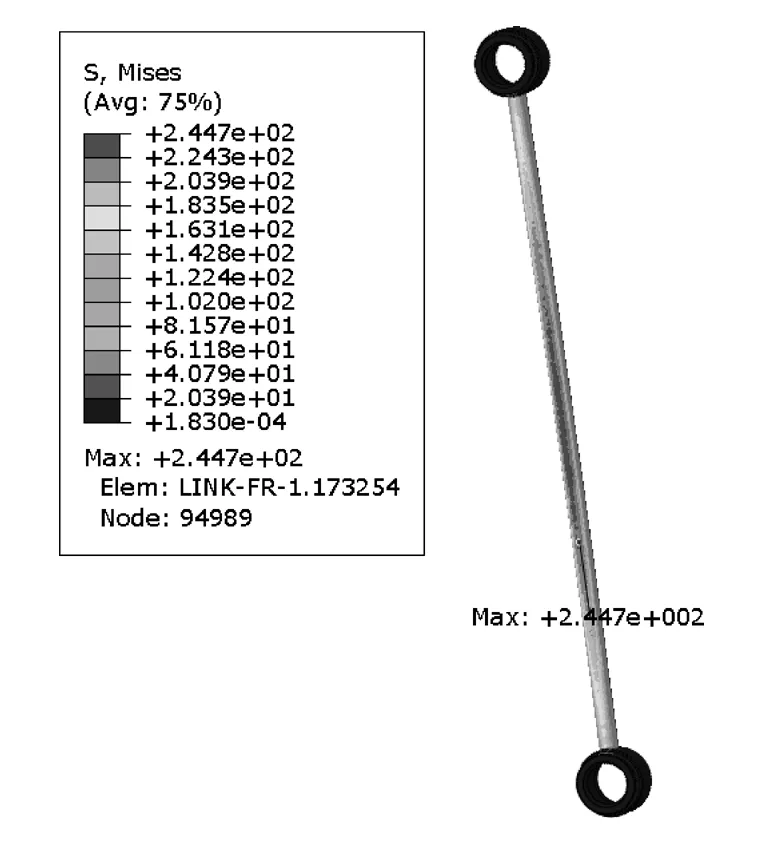
图8 杆径为8mm的稳定杆连杆应力云图
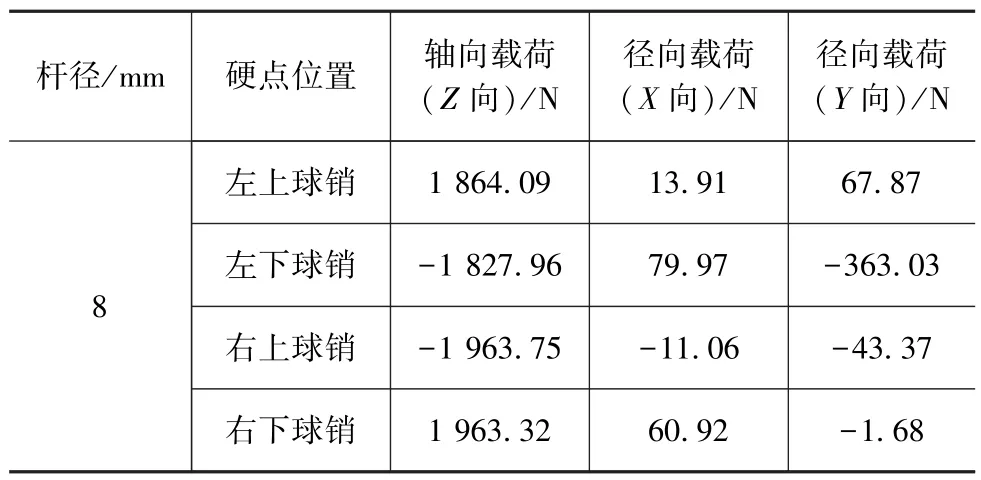
表5 杆径为8mm的硬点载荷
3.2 失稳理论和台架试验校核
3.2.1 压杆失稳理论校核
此时稳定杆连杆参数为:杆径 8mm,长度300mm,得到失稳临界压力和临界应力分别为F′cr=4535.17N,σ′cr=90.27MPa。
3.2.2 台架试验
试制小批量杆径为8mm的稳定杆连杆,选取20根进行压杆台架试验,记录屈服时刻的压力,如表6所示。其临界载荷均值为F′test= 2736.5N。
3.3 实车验证
将杆径为8mm的稳定杆连杆按图4(a)所示贴应变片后进行装车测试,测试结果见表7。由表7可见,最大压缩载荷为极限转向2工况的1 982.4N。且在极限工况3次循环后,稳定杆连杆弯曲,与有限元预测结果完全一致,如图9所示。
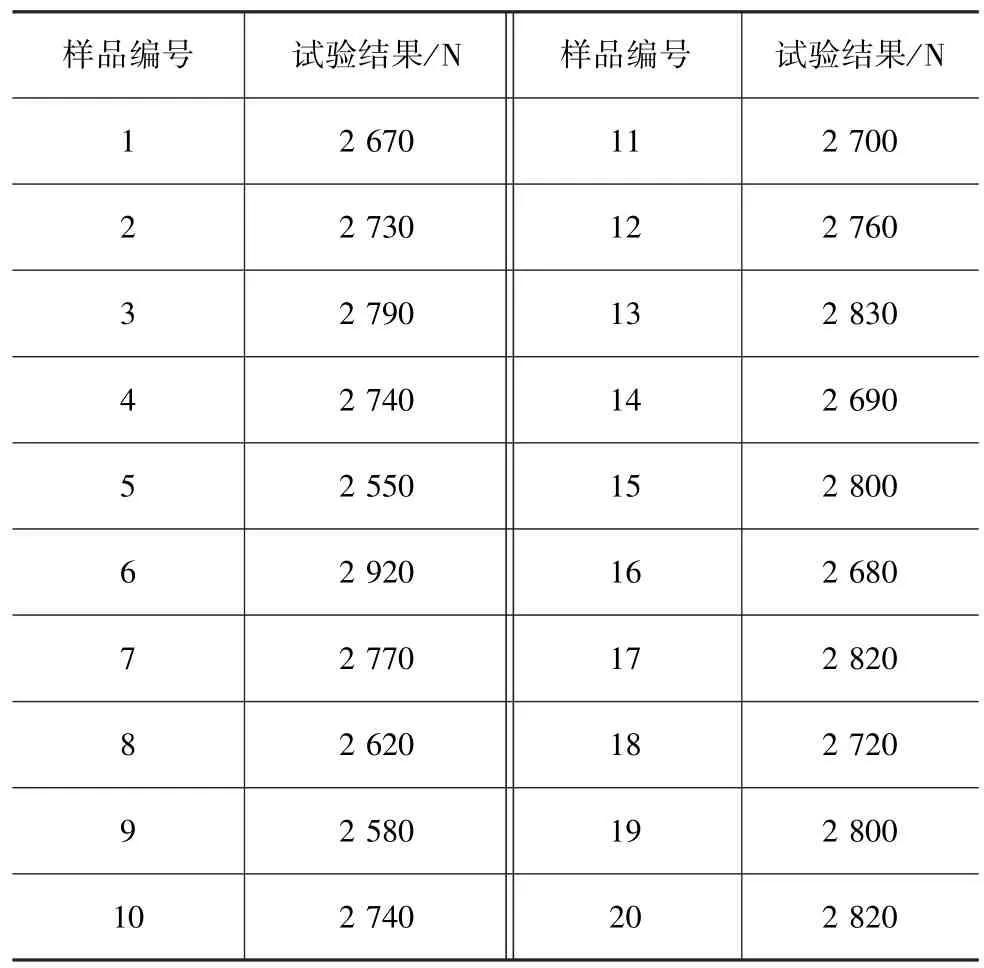
表6 杆径为8mm的台架试验结果
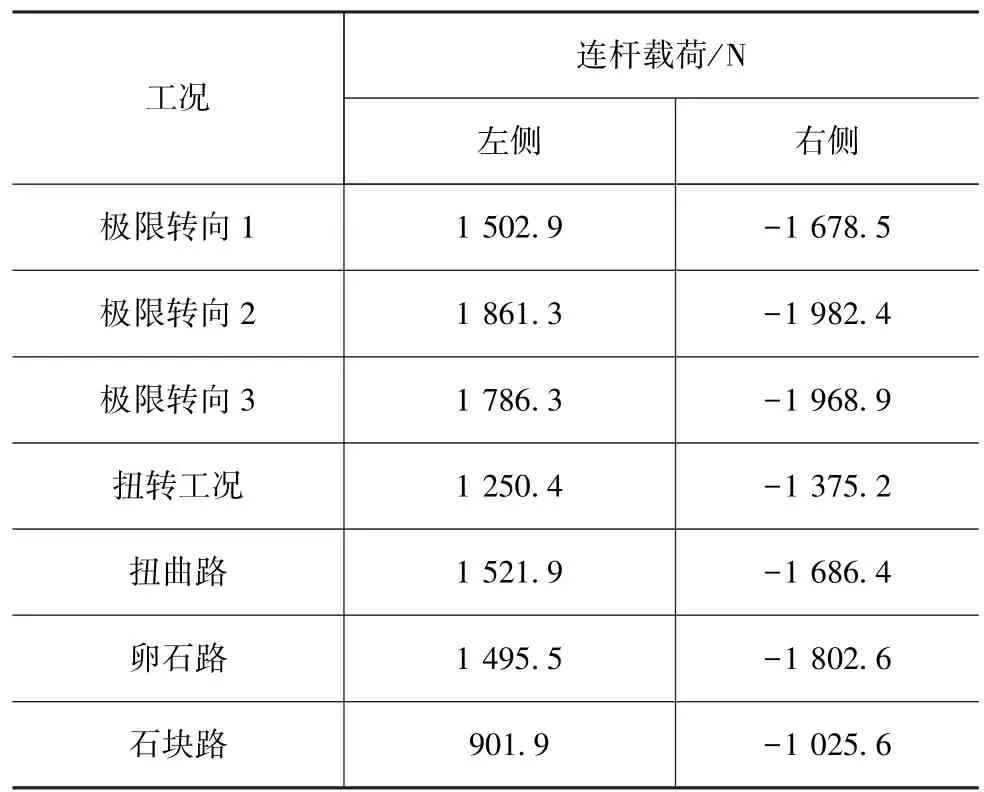
表7 同时刻下悬架轮跳量和连杆载荷

图9 稳定杆连杆弯曲
将3种方法校核结果与实车验证汇总见表8,对比可知,稳定杆连杆的有限元模型与实车验证结果完全一致,即8mm杆径为该车型稳定杆连杆的临界尺寸,无设计安全余量;而相同情况下,失稳理论和台架试验校核结果均未能预测出该杆径下的稳定杆连杆有弯曲风险。
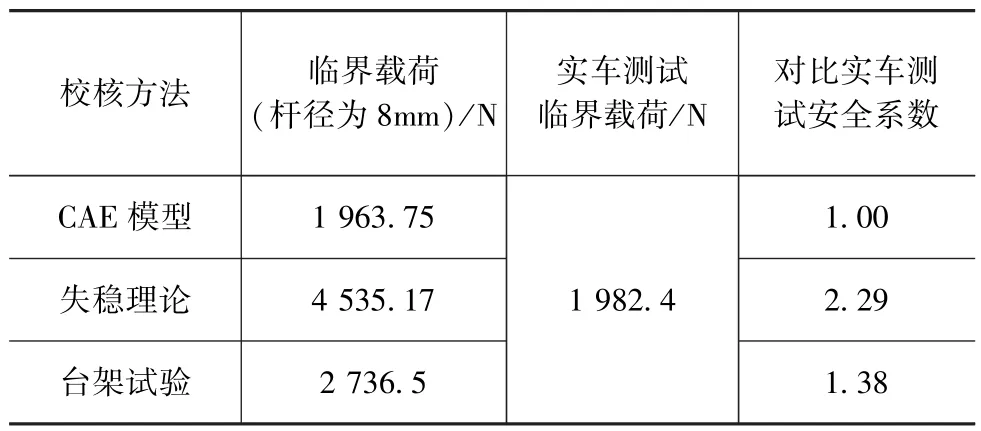
表8 结果汇总
4 结论
提取杆径为10和8mm的有限元模型的连杆两端载荷,其径向载荷都不为零,表明该连杆并非仅存在杆径方向(轴向)的受力。而失稳理论和台架试验都将稳定杆连杆简化为仅承受压缩载荷,与实际受力存在差异。
(1)失稳理论的理想压杆模型忽略了连杆两端的结构形式,且仅承受纯压缩载荷,即圆柱杆在杆径方向受压的模型。本文中的验证结果表明,失稳理论不能直接用于该零件的校核。
(2)压杆台架试验虽然施力位置与实车一致,但亦是将稳定杆连杆简化为受压情况考虑,与实车受力状态有差异,故其强度测试结果存在一定误差。
(3)通过Abaqus建立基于悬架系统非线性特性的稳定杆连杆强度分析模型,充分考虑稳定杆连杆在悬架中的运动和受力状态,可非常精准地校核稳定杆连杆的应力情况。
