插电式混合动力公交车电池配置和能量管理策略协同优化的研究∗

解少博,辛宗科,李会灵,刘 通,魏 朗

(1.长安大学汽车学院,西安 710064； 2.北京理工大学,电动车辆国家工程实验室,北京 100081)

前言

插电式混合动力汽车因可从电网给电池充电，既能发挥纯电动模式下零排放的优势，还可以提升整车的燃料经济性，且在长距离出行时克服了里程焦虑，已受到世界各国研发机构和生产厂商的高度关注[1-2]。

从成本控制的角度来看，动力电池在整车购置成本中占有重要比重。一方面，配置较多的电池，可以更好地发挥电能成本低的优势，从而降低其能耗成本；但另一方面也将使购置成本增大。因此，合理地选配电池并设计能量管理策略对于控制整车的综合成本具有重要意义。

插电式混合动力汽车作为一个多能源系统，如何管理多种能源，使其以最优的模式工作，从而降低能耗，对于降低整个生命周期内的能耗成本尤为重要。在能量管理策略方面，基于规则的电量消耗-电量维持(CD-CS)策略已在实车上得到普遍应用[3]。而基于优化理论的策略，如动态规划(DP)被广泛用于离线优化，且已成为衡量其它能量管理策略的标准[4-5]。此外，还有基于庞特里亚金极小值原理(PMP)的全局优化能量管理策略[6-7]。为更好地面向实时应用，研发人员又提出了等效能耗最小化策略(ECMS)和预测型能量管理策略等方法[8-9]。

文献中大多基于给定电池进行能量管理策略的研究。事实上，如果从用户角度出发，在插电式混合动力汽车的全生命周期内，不仅要考虑整车相比传统车辆的节能成本，同时也须关注电池的购置成本，以达到综合成本的最小化。另外，从能量管理策略的角度来看，PMP方法相比于DP在计算耗时方面有明显的优势，且容易启发出等效能耗最小化策略(ECMS)。

基于上述考虑，本文中针对一款插电式混合动力城市客车(plug-in hybrid electric bus，PHEB)构建了包含电池成本和能耗成本的综合成本最小化优化方法，分析不同行驶里程需求和电池单价对电池配置的影响；同时，基于选择的一组优化电池参数，进行能量管理策略分析，并将PMP策略与DP，ECMS和CD-CS策略进行对比分析。

1 PHEB动力系统与数学模型

1.1 动力系统结构

所研究的PHEB拓扑结构如图1所示，动力系统为串联式结构，发动机和ISG电机组成发动机-发电机单元(EGU)，两个轮边驱动电机分别与定速比减速器连接驱动车轮行驶。

1.2 动力系统模型

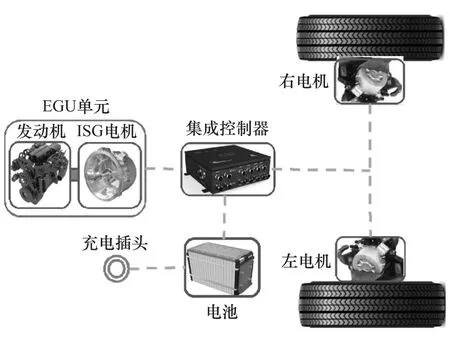
图1 PHEB动力系统结构图

EGU中的发动机为一款天然气发动机，其能耗Map如图2所示。ISG电机为永磁同步电机，通过法兰与发动机直接连接，其效率特性如图3所示。

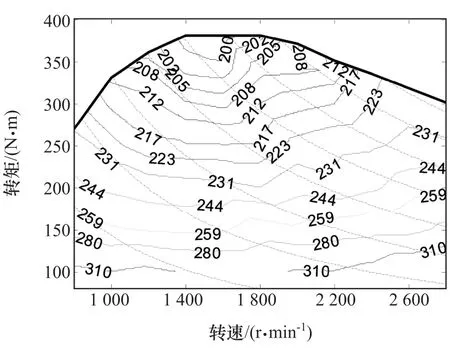
图2 发动机能耗图

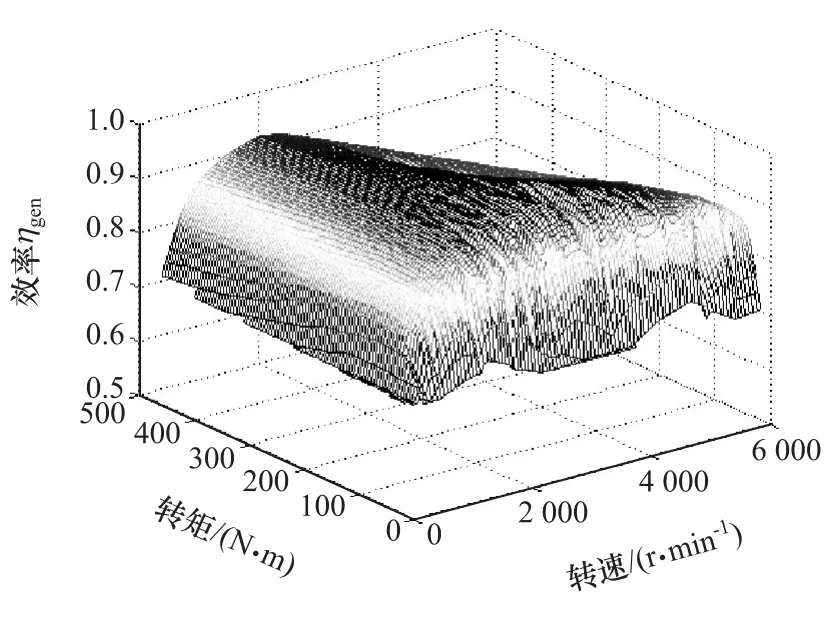
图3 ISG电机效率特性图

双侧轮边电机为永磁同步电机，其效率特性如图4所示。

1.3 电池模型

选择中航锂电生产的磷酸铁锂电池为动力电池，单体电压为3.2V，标称容量为180A·h。电池外特性基于Rint模型得到[10]，即将电池看作由开路电压Uoc和等效内阻Rb串联组成的电路，且两者均为SOC的函数。

图4 轮边电机效率特性图

结合所选电池单体容量，并考虑到本文中主要关注电池电量大小对综合成本的影响，采用串联成组的方式组成电池组。

1.4 整车参数

配置不同电量的电池将影响到整车的总质量，整车质量m可表达为

式中：m0为不包括电池在内的整车质量；Nb为单体电池数量；mcell为单体电池质量，设其能量密度为10kg/(kW·h)。

本文原型车的主要参数如表1所示。

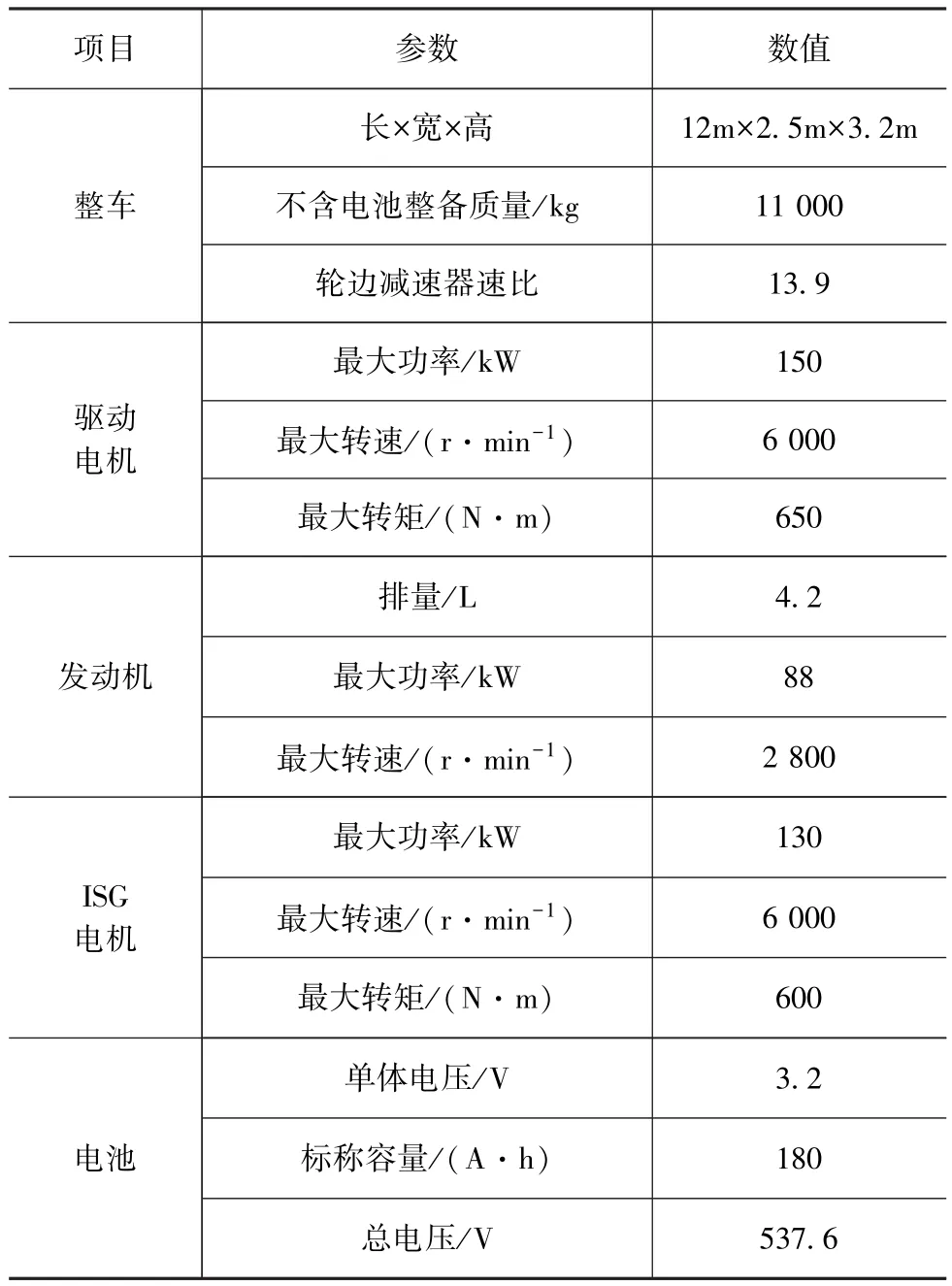
表1 整车和动力部件参数

1.5 整车试验

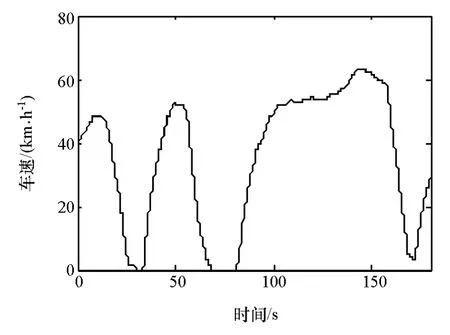
图5 车辆速度

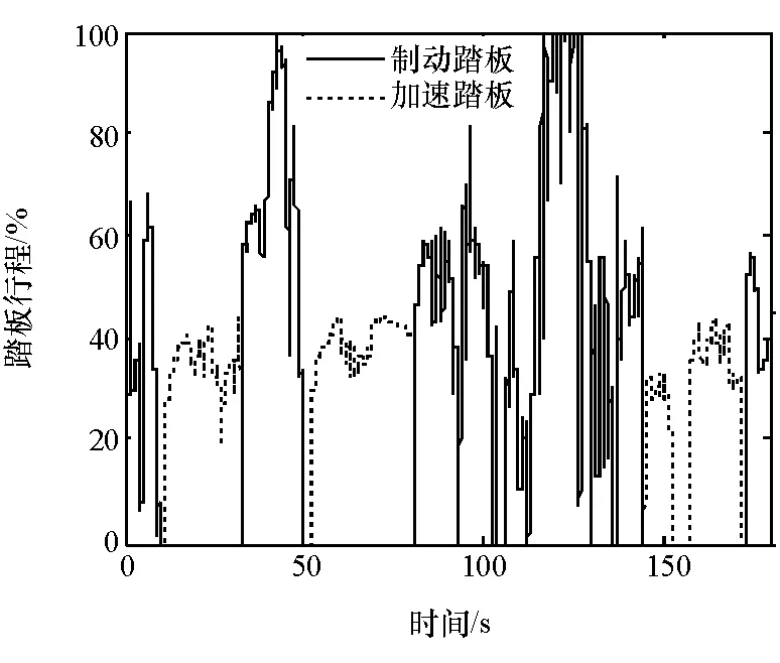
图6 加速和制动踏板行程

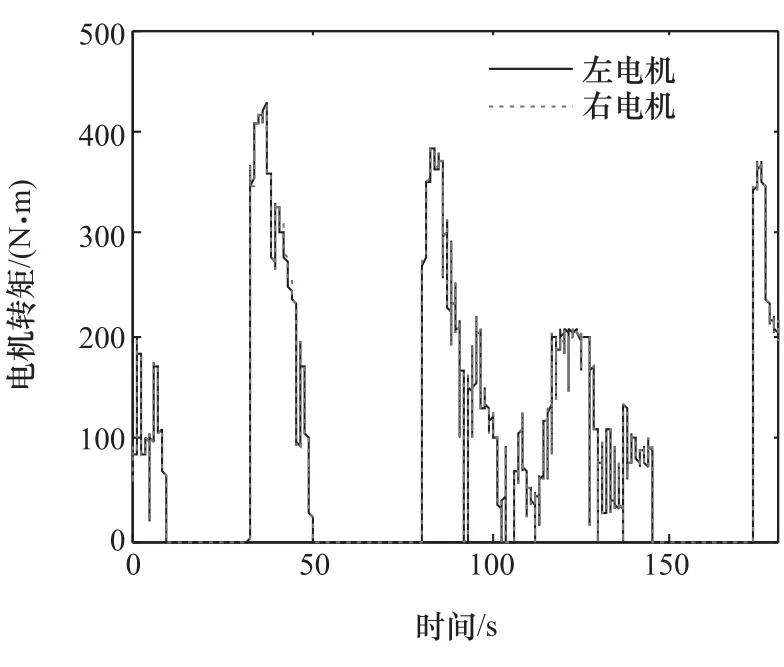
图7 左右电机转矩

本文中的原型车采用了CD-CS策略，对车辆进行实车试验并采集纯电动状态下的试验数据进行分析，车速变化如图5所示。整个行驶过程持续180s，车辆处于不断加、减速运行状态，对应的加速和制动踏板行程如图6所示。两侧电机的转矩输出如图7所示。图8为左右电机、母线和发电机的电流变化，可以看到在纯电阶段发电机组不向外输出电流，而左右电机电流、母线电流和发电机电流四者的代数和为零，即四者维持平衡关系。SOC由初始的65%下降至62%，见图9。计算可知，试验过程消耗的电能为10.451MJ。同时，基于试验车速和初始SOC值，并结合电机、电池等动力传动系统模型和整车模型，在Matlab/Simulink平台仿真得到整个过程的电耗为10.243MJ，即仿真能耗与实车能耗十分接近。

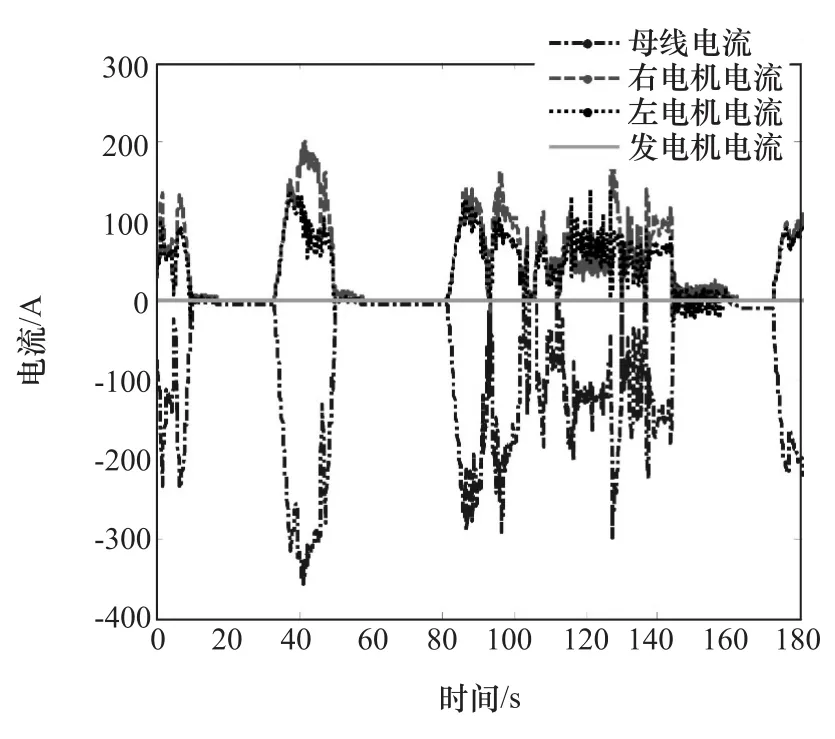
图8 电流变化

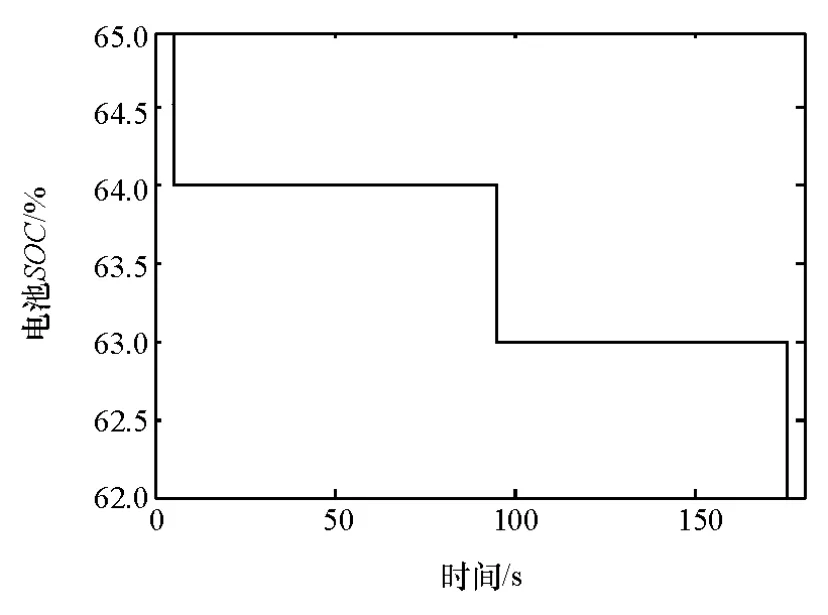
图9 电池SOC变化

2 协同优化模型

2.1 目标函数

整车综合成本涉及配置电池的电量大小、电池的单价、燃料的单价、电价和维修保养成本等多重因素，但考虑到燃料单价、电价和维修保养成本这些因素相对变化不大，本文中主要以全生命周期内的电池购置成本和能耗成本组合而成的综合成本最小化为目标函数，它等效为单次循环工况的能耗成本与等效电池购置成本之和，即目标函数为

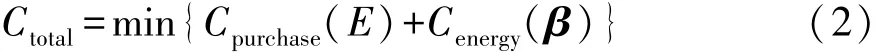
式中：Cpurchase为单次循环工况的等效电池购置成本；Cenergy为单次循环工况的能耗成本；Ctotal为单次循环工况的综合成本。

优化变量为E和β，其中，E表示配置的最优电池度数(即总电量)，β表示在给定工况下EGU输出功率占需求功率的比值序列，为矢量。则最优的电池度数和功率比值序列可表示为

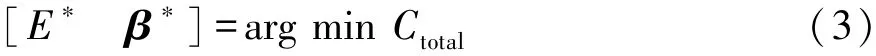
在计算过程中，用电池组数对应电池电能，用EGU输出功率PEGU对应每一时间步长该值与需求功率的比值关系。

单次循环工况的电池等效购置成本可表示为

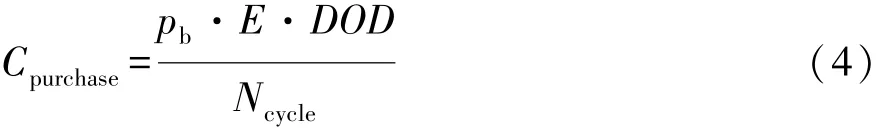
式中：pb为电池单价，元/(kW·h)；E为电池电量，kW·h；DOD为电池的放电深度；Ncycle为电池整个生命周期内的循环次数，计算时设为3 500次。

单次循环工况下的能耗成本为

式中：pe和pf分别为电和天然气的单价；Me和Mf分别为单次循环工况下的电耗和气耗。计算时设天然气和电能的单价分别为4.3元/L和0.8元/(kW·h)。

2.2 协同优化模型

考虑到综合成本涉及到配置电池的度数和基于不同电池度数下的能量管理策略，因此实现综合成本最小化的优化模型结构选择为双环结构，如图10所示。其中，外环为配置不同度数的电池，内环为选定电池度数下的基于PMP方法的能量管理策略。

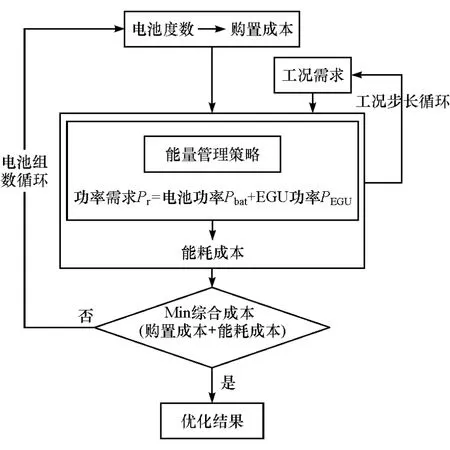
图10 电池配置和能量管理协同优化模型

3 基于PMP的能量管理策略

考虑到PMP算法是一种全局优化策略且其计算效率高于DP算法，因此，对于本文中PHEB的能量管理基于PMP算法进行优化。

3.1 基于PMP的能量优化问题

所研究的PHEB包含动力电池和EGU两种动力源，但考虑电价远低于燃气价格，在此忽略了电池电能的消耗。为使整个工况的能耗成本达到最小值，目标函数可表示为

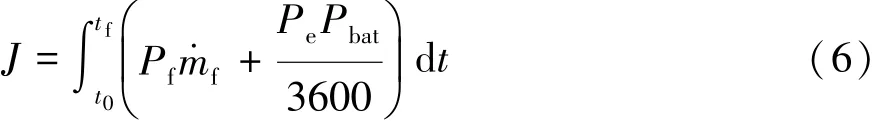
式中：J为总能耗成本，元；t0和tf分别为始末时刻，s；为 EGU 的燃气消耗率，L/s，它是 EGU 输出功率PEGU的函数；Pbat为电池消耗功率，kW。

选择SOC为状态变量，则状态方程为

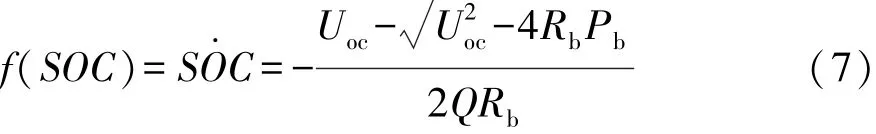
再根据庞特里亚金极小值原理，Hamilton函数可表达为

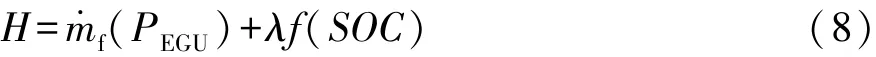
式中：H为Hamilton函数值；λ为协态变量。

可得系统的协态方程为

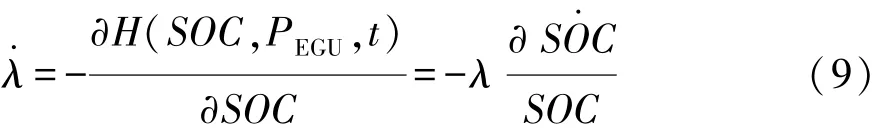
而正则方程为

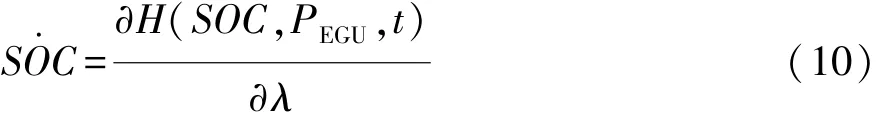
电池SOC的约束条件为

式中SOC0和SOCf分别为行驶工况的SOC始末值。

3.2 数值解法

基于PMP的能耗成本最优化问题可归结为两点边值问题[11]，可以通过打靶法求其数值解。同时采用弦截法进行协态变量的调整，其表达式[13]为

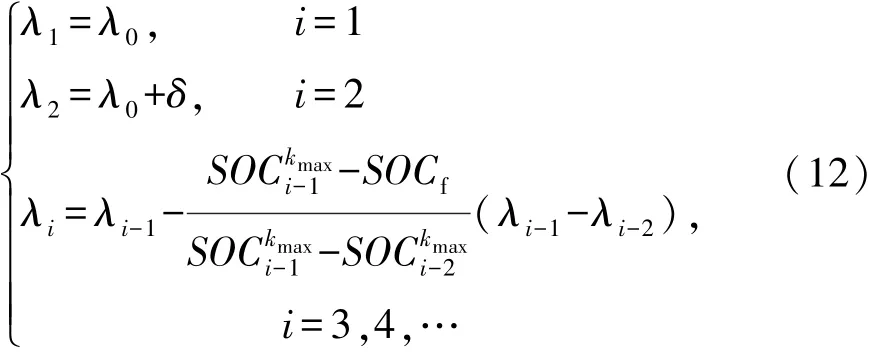
式中：λ0和δ为前两次打靶过程中确定初始协态变量的给定常数；i为打靶序列；kmax为工况长度。

4 综合成本影响因素分析

基于连续的中国典型城市客车运转循环(CCBC)[12]，合成不同的行驶里程需求，共分3种情况：12个 CCBC共计 69.6km；14个 CCBC共计81.2km；16个CCBC共计92.8km。同时，选择电池成组的单体组数为60～160，对应的电池能量范围为34.56～92.16kW·h。考虑到电池的技术水平和市场规模等因素，设电池单价变化范围为900～1 600元/(kW·h)。另外，设电池在使用时的SOC取值区间为0.3～0.8。打靶法中的收敛精度为0.001，协态变量初值λσ和δ分别为4.0和0.01。

当需求行驶里程为12个CCBC约69.6km时，得到的配置电池度数与单次行程综合成本关系如图11所示。由图可知，当电池单价在900～1 100元/(kW·h)时，最佳的电池配置为88.7kW·h；当电池的单价增至1 200元/(kW·h)时，配置的电池最佳度数为86.4kW·h，而当电池单价上升到1 300和1 400元/(kW·h)时，最佳结果分别降至78.3和63.4kW·h；当单价上升至1 500～1 600元/(kW·h)时，选择55.3kW·h的电池能使综合成本降至最低。

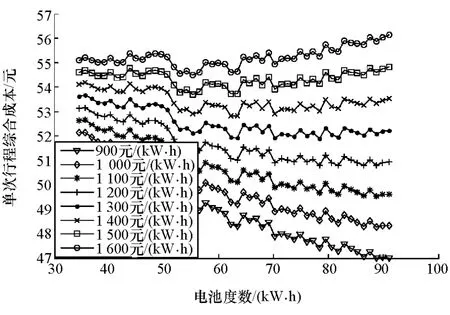
图11 12个CCBC协同优化结果

由图11可知，当电池度数一定时，随着电池单价的上升综合成本不断增加，且曲线右半部分(电池度数大于55kW·h)增加的幅度明显大于左半部分(电池度数小于55kW·h)，当电池单价上涨至1 500元/(kW·h)时，曲线右半部分要高于左半部分，即电池购置成本大幅度提升。而在特定的单价范围如900～1 100元/(kW·h)和1 500～1 600元/(kW·h)，选择的最优电池电量相同，是由于随着电池单价的增加，单次循环的综合成本增加，使曲线整体得到抬升；且随着电池度数的增大，尽管曲线右侧抬升的幅度比左侧要大，但曲线的非凸特征未能使最低点发生变化。

如果行程需求增加至14个CCBC约81.2km时，得到的结果如图12所示。可以看到，当电池单价在900～1 100元/(kW·h)时，最优点为曲线的右端点，即选择最小的电池电量能使综合成本最小；当电池单价上升至1 200～1 400元/(kW·h)时，配置的最佳电池度数为65.7kW·h；当电池单价继续上升至1 500和1 600元/(kW·h)时，最佳电池度数分别降至54.1和51.8kW·h。

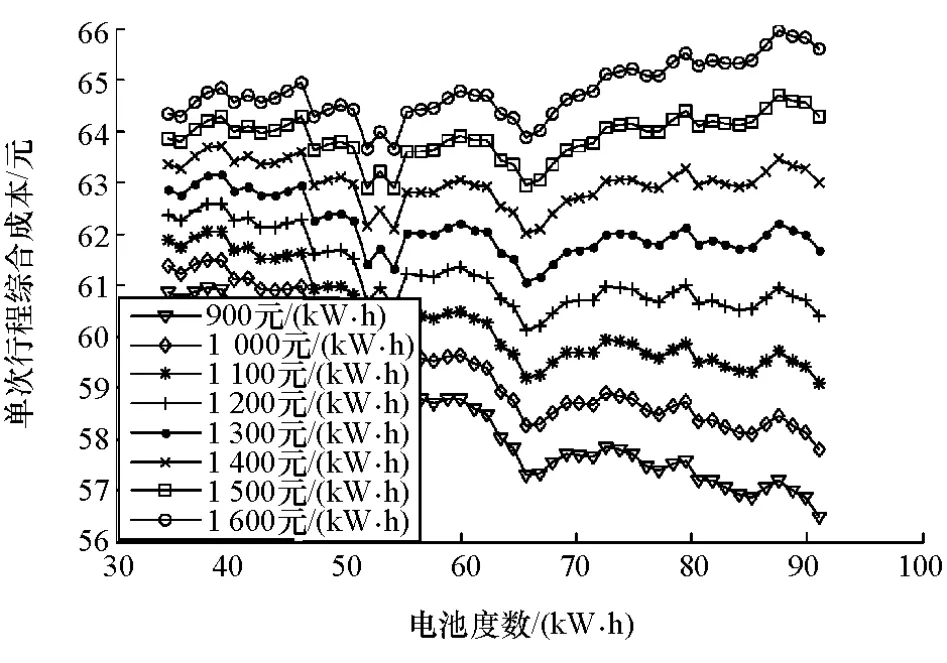
图12 14个CCBC协同优化结果

当需求的行驶里程达到16个CCBC约为92.8km时，计算得到的协同优化结果如图13所示。可以看到：当电池单价为900～1 100元/(kW·h)时，最优的电池度数为86.4kW·h；当电池单价从1 200元/(kW·h)上涨至1 300元/(kW·h)时，最优的电池度数降至69.1kWh；而当电池单价增长至1 400～1 600元/(kW·h)时，最优电池能量下降至51.8kW·h。

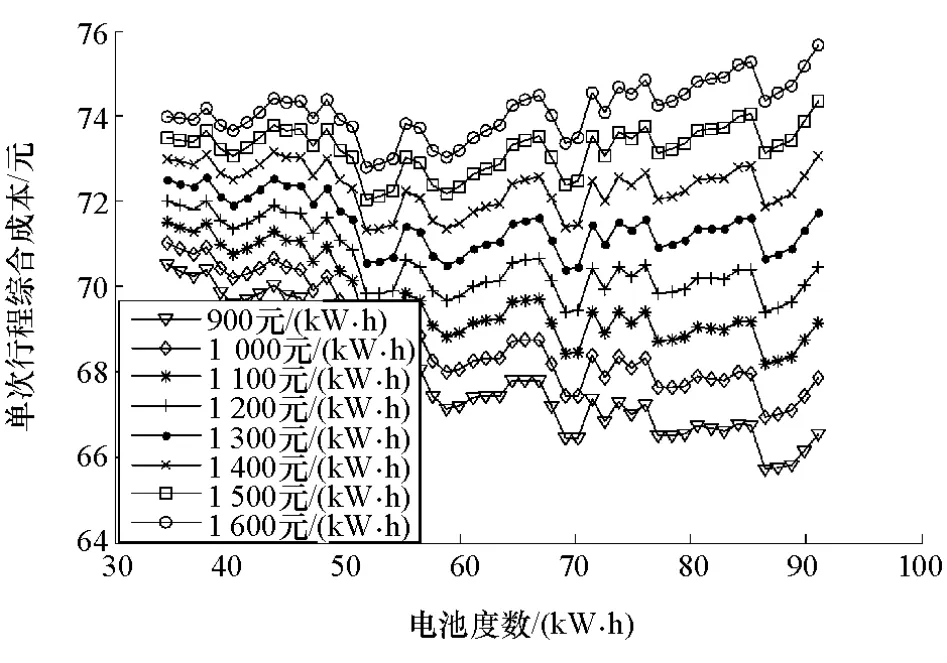
图13 16个CCBC协同优化结果

对比不同里程需求和电池价格的计算结果可以发现：当行程给定，最佳电池电量随着电池价格的上升不断减小；而当价格一定，不同的行程需求则有不同的最优电池配置电量，即电池购置成本和能耗使用成本在不同的里程需求和电池单价条件下始终在进行博弈，需要协同优化才可以找到使综合成本达到最小的电池配置。

5 算例分析和能量管理策略对比

基于特定的行驶里程要求和电池单价(14个CCBC共计81.2km，电池单价1 400元/(kW·h))，进行协同优化计算，得到的最优电池能量为65.7kW·h，对应的电池组数为114，电压为364.8V。

基于计算得到的最优电池配置，分别应用PMP，DP和CD-CS策略进行工况仿真，并进行对比分析。其中，CD-CS策略设定的规则为：当SOC下降至0.30时，EGU开启并向外输出40kW的恒定功率；当SOC上升至0.35时EGU关闭，整车维持在纯电动运行状态。

首先，基于打靶法进行PMP策略的数值求解，得到的SOC轨迹如图14所示。由图可知，共需6次打靶即可达到最优SOC轨迹，可以看到采用的弦截法通过不断调整初始协态变量使SOC终值逐渐接近下边界。由最后一次打靶过程可以得到最优的协态变量轨迹，如图 15所示，协态变量从初值3.974g/h逐渐下降至末值3.888g/h。

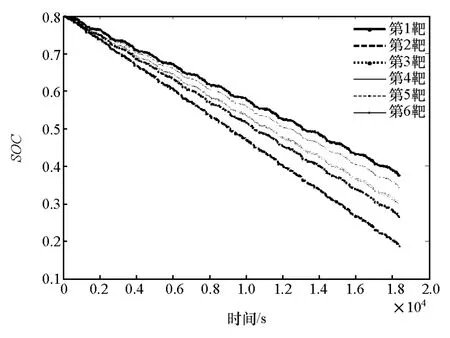
图14 打靶过程的SOC轨迹

基于PMP策略得到的最优协态变量可以启发出EMCS策略的等效能耗转换因子，本文中选择PMP策略的协态变量终值作为等效因子：

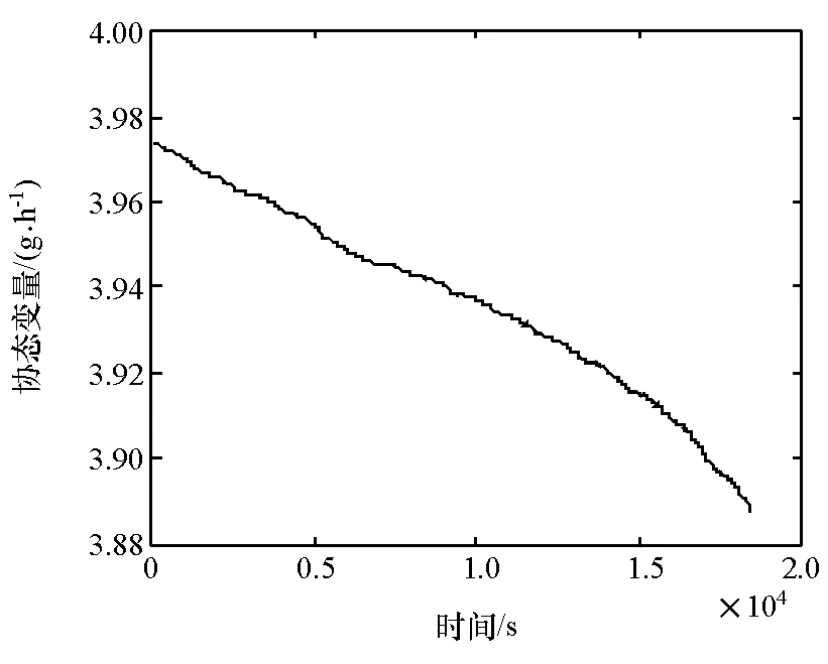
图15 末次打靶中协态变量的变化

PMP，DP，ECMS和CD-CS 4种能量管理策略的定量计算结果如表2所示。可以看到：CD-CS的能耗成本最高；PMP的能耗成本最低。同为全局优化策略，基于PMP的能耗略低于DP的结果，其原因是由于DP在数值计算过程中须对变量进行离散和对累积成本进行估算，这会导致计算精度降低。另外与CD-CS策略相比，基于PMP策略的能耗降低约17.5%。ECMS策略的能耗成本与DP和PMP两种全局优化算法的能耗成本十分接近。

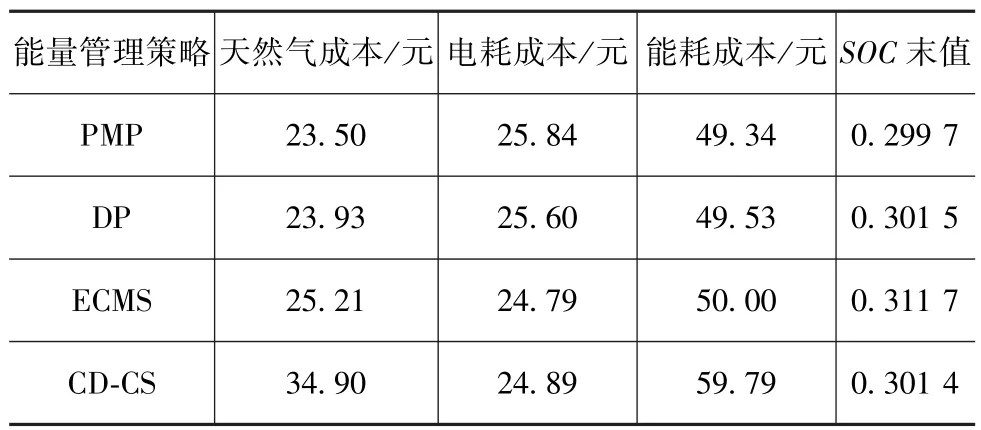
表2 4种能量管理策略能耗比较

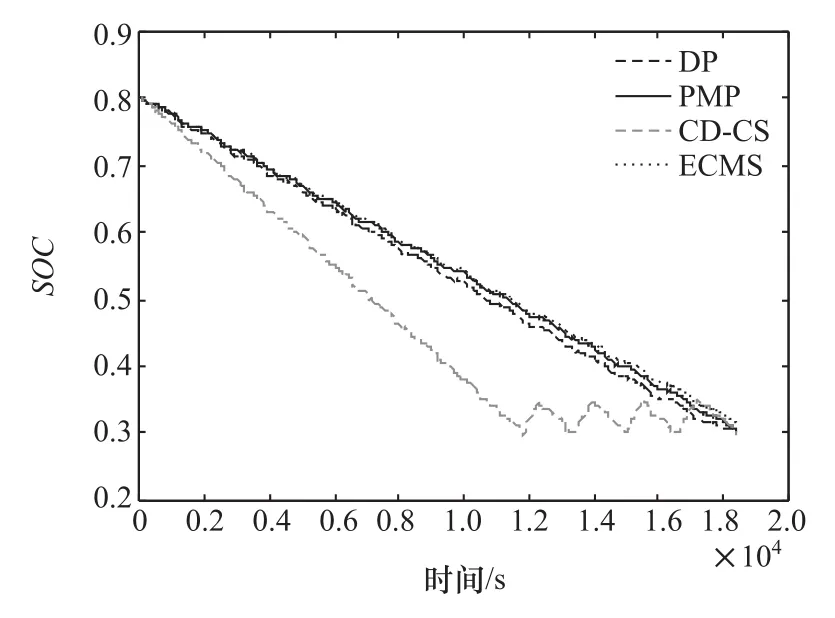
图16 4种能量管理策略的SOC轨迹

图16 给出了4种能量管理策略得到的SOC轨迹。可以看到：基于规则的策略明显划分为电量消耗和电量维持两个阶段；DP和PMP作为全局优化策略，两者所得SOC轨迹存在差异，主要原因是这两种优化算法具有不同的优化机制；由PMP求得的协态变量并得到ECMS策略的SOC轨迹与DP和PMP策略所得轨迹十分接近。

6 结论

针对一款插电式混合动力公交车，以电池购置成本和能耗成本组成的综合成本最小化为目标，进行电池配置和能量管理策略的协同优化研究。构建了考虑电池购置成本和能耗成本的协同优化双环结构，其中外环选择不同的电池电量，内环为基于PMP算法的能量管理策略。基于不同行驶里程需求和电池单价的分析表明，最优的电池能量配置与行驶里程长短和电池单价等因素相关，只有通过协同优化计算才能得到电池电量的最优值。同时，分别应用PMP，DP，ECMS和CD-CS策略进行一组最优电池配置下的工况仿真。结果表明：基于PMP策略的能耗成本与DP接近；与CD-CS策略相比，基于PMP策略的能耗降低约17.5%；ECMS策略的能耗与全局优化算法的能耗十分接近。