平衡轴总成配合间隙对整车动力学的影响∗

黄 康,杨 羊,甄圣超,易 勇

(合肥工业大学机械工程学院,合肥 230009)

前言

汽车整车动力学模型是平顺性和操纵稳定性等研究的重要内容，现今针对汽车整车建模方法有很多，围绕不同的建模方法已有不少研究成果，传统常规的方法有牛顿动力学方法和拉格朗日方程等。文献[1]和文献[2]中运用牛顿动力学方法建立了多自由度整车动力学方程，并验证了其正确性；文献[3]中运用拉格朗日方法，得到了整车模型，对实际工程应用有很高的指导意义；文献[4]中建立了三轴拖车的动力学模型，并用软件仿真和实验测试，验证了模型的可靠性；除了传统方法外，文献[5]中将有限元的思想运用到汽车动力学模型的建立中，将振动结构离散化，采用节点位移法得到系统模型，是一种比较新颖的方法。在整车模型的基础上，人们还对汽车关键零部件对整车动力学性能的影响做了大量的研究。文献[6]中在研究汽车平顺性时，考虑了一种新型轮胎的影响；文献[7]中考虑了汽车橡胶件对平顺性的影响；还有一些研究对悬架的钢板弹簧、橡胶件等关键零部件进行了分析[8-10]，取得了显著的成果。平衡轴总成作为多轴重型汽车悬架的关键部件，在汽车运行过程中起到均载的作用，对汽车竖直方向的动力学特性影响较大。

目前尚未有报道关于多轴重型汽车平衡轴总成中的配合间隙对整车动力学性能的研究。平衡轴的芯轴和板簧座通过弹性金属衬套连接，在长期重载条件下，由于磨损和弹性变形，存在较大的配合间隙，它对整车的振动和冲击影响较大，在建模中考虑其特性具有重要意义。本文中借鉴含间隙机构动力学相关理论[11-15]，对平衡轴配合间隙进行了运动学建模，并代入系统m模型中，得到非线性系统模型，并与理想模型对比，突出其影响特点。

1 考虑配合间隙的平衡轴运动学模型

在三轴重型汽车悬架中，平衡轴总成起到一个铰链的作用，当前、中、后桥输入位移不在同一直线上时，中后桥链接板簧绕铰链中心点旋转，使三轴同时触地，达到平衡载荷的作用。在系统的动力学建模中，当不考虑芯轴与板簧座之间的配合间隙时，平衡轴总成可视为理想铰链，但在实际情况下，芯轴与板簧座之间存在间隙，尤其是采用弹性较大的材料作为衬套时，在重载的情况下，配合间隙较大，对整车的动力学性能影响较大。

货车重载时，通常板簧座中心始终在芯轴中心上方，板簧座内孔表面始终与芯轴外圆表面相切。不考虑芯轴和板簧座的弹性变形，将芯轴和板簧座等效为孔 轴配合，设工作过程中孔转角为ψ，孔与轴配合间隙为e，考虑配合间隙的平衡悬架系统简化模型如图1所示。

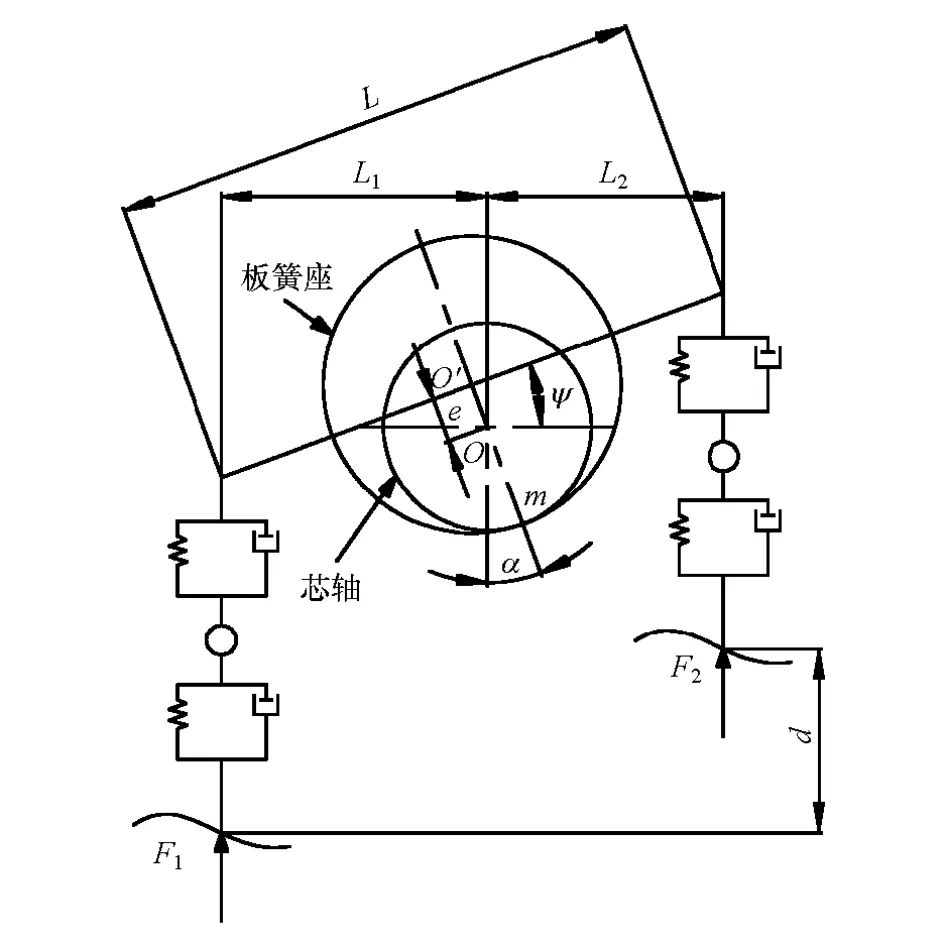
图1 考虑配合间隙的平衡悬架系统简化模型

图中：O为芯轴中心；O′为板簧座中心；α为孔与轴的相对转角，为图中直线OO′与竖直面夹角；m点为芯轴外圆表面与板簧座内孔表面切点；L为平衡轴总成的总长度；L1为中桥与平衡轴中心的距离；L2为后桥与平衡轴中心的距离；d为工作中平衡轴总成左右两侧的高度差。

分析轴与孔相对运动关系时，假设轴固定，孔绕轴相对转动，且不考虑滑动、滚动同时存在的情况，设最大静摩擦力等于滑动摩擦力。当孔向一侧转动(即ψ值增大时)，首先轴和孔在静摩擦力的作用下相对滚动，O′点绕O点作半径为e的圆周运动，当摩擦力达到最大静摩擦力时，ψ继续增大，摩擦力变为滑动摩擦力，O′点相对O点保持静止，α值保持不变。当ψ值达到最大值后孔反向转动时，轴与孔运动关系先后由滑动变为滚动，当处于滚动时O′点绕O点做反向圆周运动，如此循环往复，形成了轴与孔之间的运动学关系，O′的运动轨迹为一圆弧区域。根据孔 轴配合间隙，对一个周期内的运动过程进行讨论，为了使分析简单，对模型进行以下设定：

(1)当初始时间 t＝0时，α和 ψ的初始值都为0；

(2)逆时针转动时ψ值增大，顺时针转动时ψ值减小；

(3)假设轮胎通过的道路为低洼地面，即ψ值先增大后减小；

(4)设ψt表示t时刻ψ的值，由图1可知ψt＝arcsind/L。

根据摩擦学原理，孔与轴的相对转角α的最大偏移角(其中μ为接触表面滑动摩擦因数)为

孔与轴的相对转角α的最小偏移角为

由以上假设条件可以作出ψ角在一个周期内的变化曲线，如图2所示。当孔的转角ψ达到极值时孔的角速度ψ·＝0，在t2时刻ψ达到最大值ψ＝ψmax；在t5时刻ψ达到最小值ψ＝ψmin＝-ψmax。

由图2可以看出，在区间[0，t1]上，轴与孔的相对运动关系为滚动，此时α和ψ的表达式为

在区间[t1，t3]上，轴与孔的相对运动关系为滑动，此时α和ψ的表达式为

在区间[t3，t4]上，轴与孔的相对运动关系为滚动，此时α和ψ的表达式为

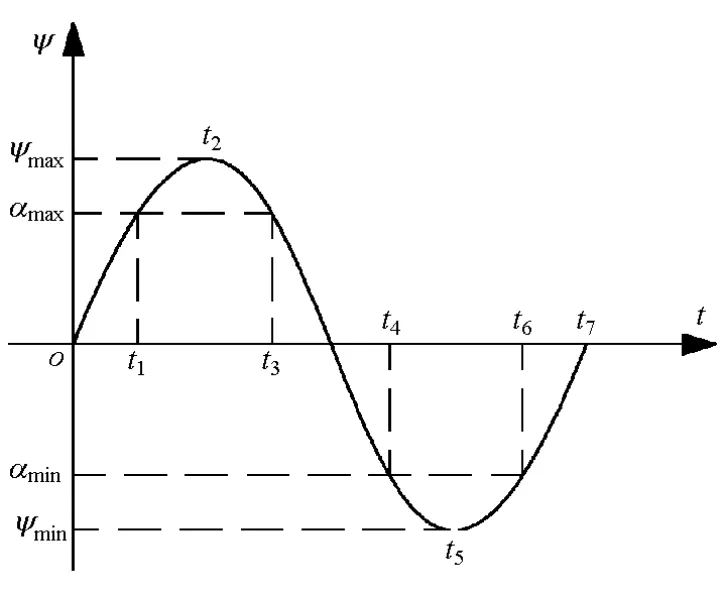
图2 ψ角在一个周期内的变化情况

在区间[t4，t6]上，轴与孔的相对运动关系为滑动，此时α和ψ的表达式为

在区间[t6，t7]上，轴与孔的相对运动关系为滚动，此时α和ψ的表达式为

综合式(3)～式(6)可得

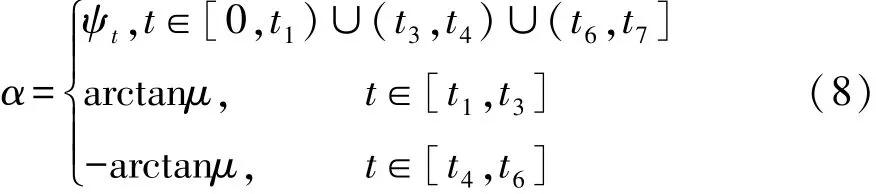
建立了孔 轴配合间隙的运动学模型后，将此模型考虑到整车系统动力学模型中，与理想线型模型相比，此非线性运动学模型在系统中的影响有两方面：一方面表现在孔中心和轴心在竖直方向上的间距变动设为Δx；另一方面表现在孔中心和轴心在水平方向上的间距变动设为Δy。误差的变动情况可表示为

式中：xO′和yO′分别为孔中心竖直和水平方向上的位移；xO和yO分别为轴心竖直和水平方向上的位移。

由式 (8)知 α ∈ [-αmax， αmax]， 故 Δx∈[ecosαmax，e]，Δy∈[-esinαmax，esinαmax]，在整个运动过程中，Δx的变动最大范围为

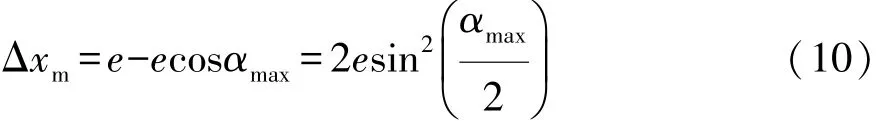
Δy的变动最大范围为

由于滑动摩擦因数很小，αmax值很小，Δxm≪Δym，故孔中心和轴心在水平方向上的间距变动对系统动力学性能的影响远大于竖直方向，在建模时可将竖直方向上的间距变动忽略不计。将含间隙平衡轴机构带入系统，可表示为

2 系统动力学模型的建立

对三轴重型汽车考虑1/2模型，在系统建模时对整车动力学性能影响不大的因素可忽略不计，简化模型如图3所示。使用传统方法建立的重型汽车简化模型，由于驾驶员和座椅质量相对车身质量很小，将汽车轮胎和悬架分别等效简化为对应的刚度和阻尼。图3中各参数符号物理意义如表1所示。

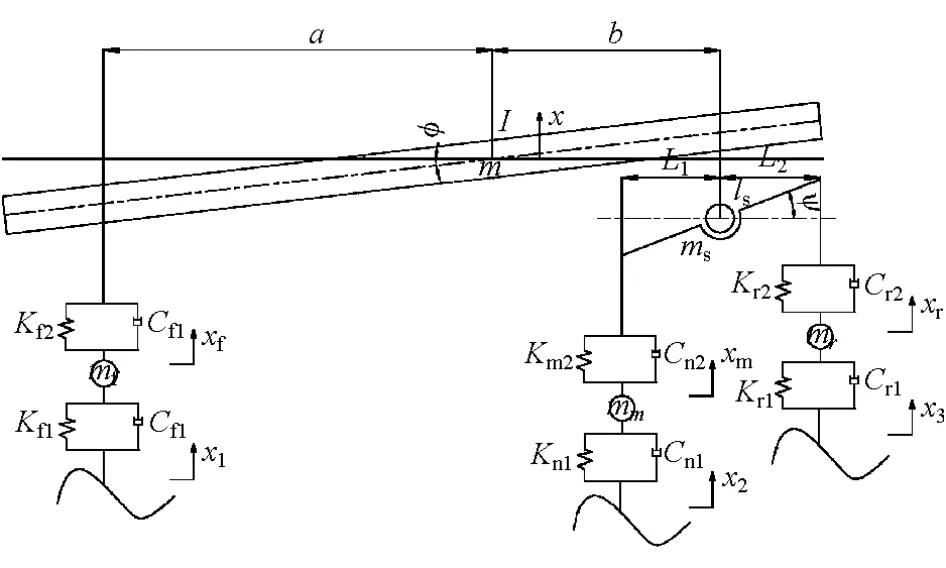
图3 三轴重型汽车1/2简化模型

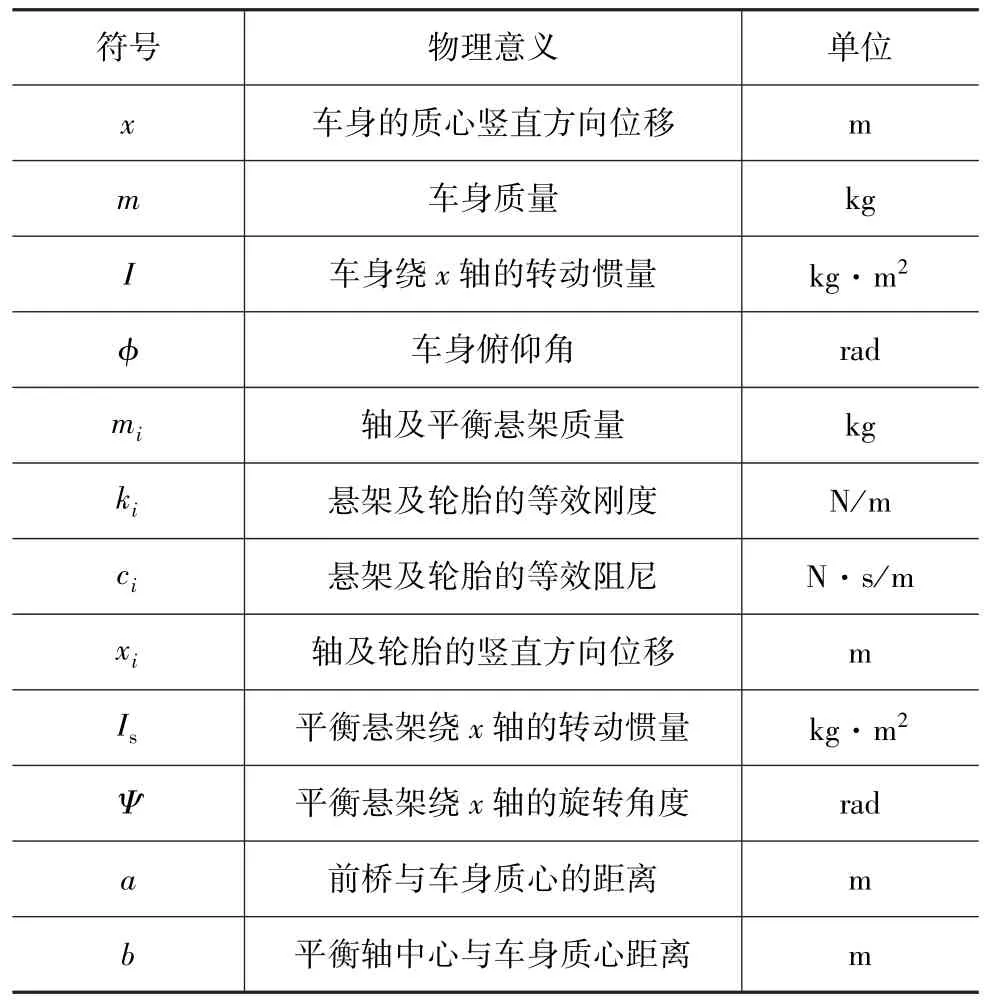
表1 整车悬架动力学模型中各参数符号的物理意义

根据多体动力学理论，系统动力学方程可表示为

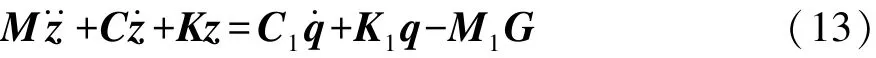
式中：M∈R6×6为系统广义质量矩阵。z∈R6为系统的广义位移；∈R6和∈R6分别为广义输出和加速度；C∈R6×6为系统阻尼矩阵；K∈R6×6为系统刚度矩阵；C1+K1q-M1G为系统输入在轮胎上产出的力及系统重力；q∈R6为路面激励对系统的位移输入；∈R6为系统输入速度；C1∈R6×6为轮胎的等效阻尼矩阵；K1∈R6×6为轮胎的等效刚度矩阵；M1∈R6×6为考虑重力的质量矩阵；G∈R6为重力加速度矩阵。

利用Lagrange原理可求得系统动力学方程中各矩阵为

其中阻尼矩阵C和刚度矩阵K中的各元素为

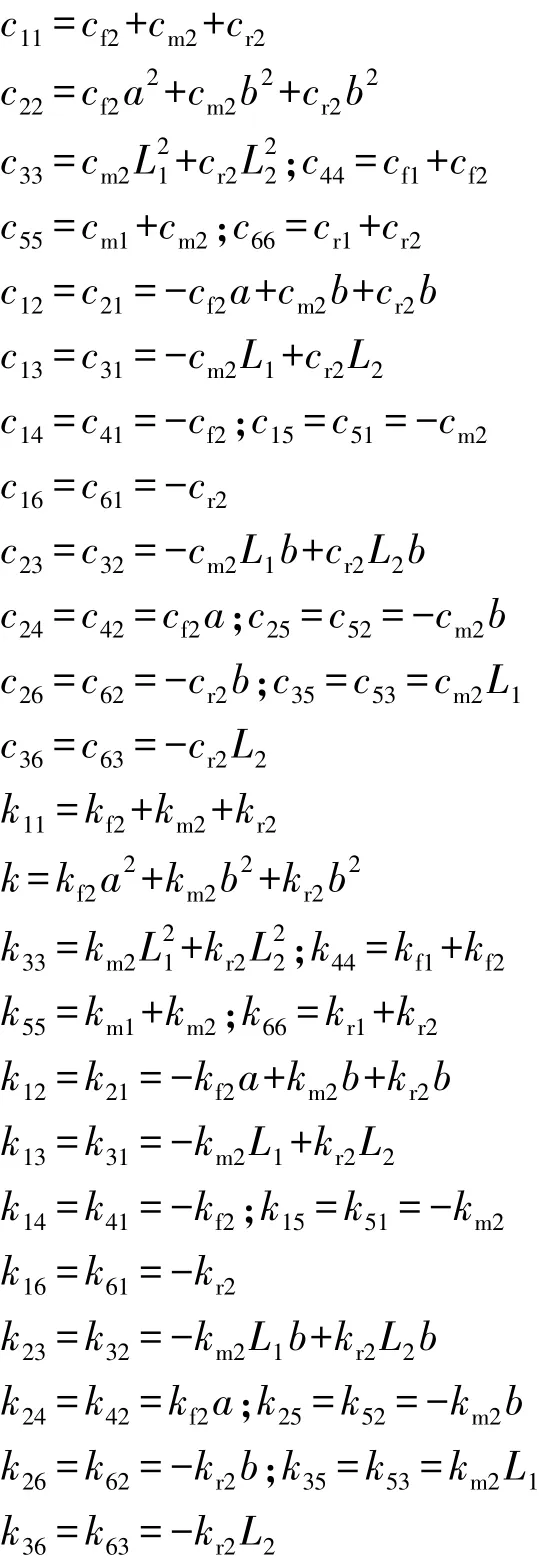
将式(12)中的L1和L2表达式代入式(13)中，就可得到三轴重型汽车系统考虑平衡轴配合间隙的动力学方程。当L＝L＝时，系统模型即为理想12模型。

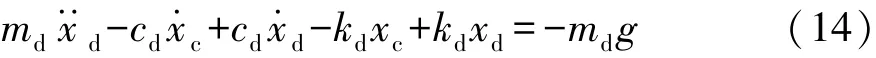
式中：md为座椅与驾驶员总质量；xd为驾驶员位移；cd为座椅下阻尼器阻尼；kd为座椅下弹簧钢度。车身上座椅对应位置位移为

式中ls为座椅到车身前端的距离。

当考虑驾驶员自由度时，简化方程为

3 系统仿真及结果分析

对某一具体汽车，计算参数为：m＝25000kg，mf＝890kg，mm＝ 1400kg，mr＝ 1400kg，ms＝ 200kg，I＝31245kg·m2，Is＝ 3210kg·m2，a＝ 3.15m，b＝1.01m，L＝1.01m，cf1＝3500N·s/m，cf2＝40000N·s/m，cm1＝cr1＝12600N·s/m，cm2＝cr2＝4000N·s/m，kf1＝1100kN/m，kf2＝350kN/m，km1＝kr1＝4400kN/m，km2＝kr2＝1400kN/m，e＝0.015m，μ＝0.15。

将数学模型用Matlab软件进行数值求解，对整车的z向位移进行动力学仿真，通过仿真可预测汽车在各种工况下z向的动态性能。

首先对理想模型进行初始状态的仿真，设置各质点初始位移、速度和加速度均为零，当汽车静止不动时，即路面对各轮胎的激励为零，仿真得到在重力作用下各自由度的运动情况，此时，随时间的变化，振动逐渐减弱，最后静止，各自由度趋于稳定值，可得到系统仿真时自由度的初始边界条件。

下面采用路面激励对模型分析，选择D级路面，前轮、中轮和后轮之间存在的相位差α1和α2可根据车速和车身尺寸算出。仿真车速v＝10m/s，根据GB/T7031—2005规定，生成3个车轮的路面载荷谱，如图4所示。对含间隙的非线性系统模型仿真，得到车身3个自由度的广义位移响应曲线，如图5所示。

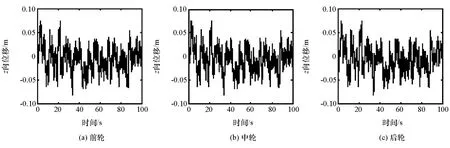
图4 各轮路面激励输入

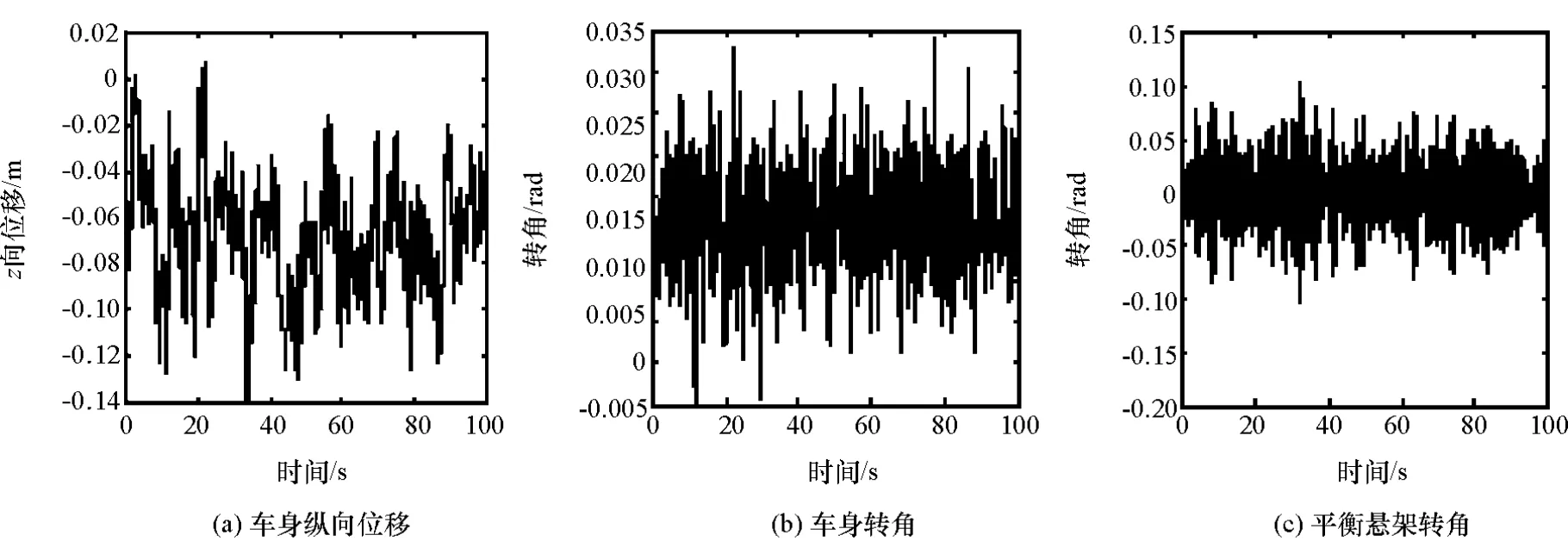
图5 非线性车身3自由度动态响应

由图5可见：汽车在D级路面上运行车身转角变化范围很小，可将sinφ等效为φ；平衡轴转角也在较小范围内变动，只有很少部分时刻达到了ψt，表明平衡轴孔与平衡轴之间运动关系绝大部分时间为滚动。此分析结果可作为汽车弹簧、阻尼和质量分布设计的参考依据。

通过车身纵向位移、转角及车身几何关系，得到驾驶员位置时域内的位移曲线，代入式(9)得到驾驶员运动情况，同时仿真计算理想动力学模型，得到两种模型驾驶员加速度的对比。为了避免初值设置不合理的影响，同时体现出两条曲线的差异，截取仿真时间20-30s，如图6所示。

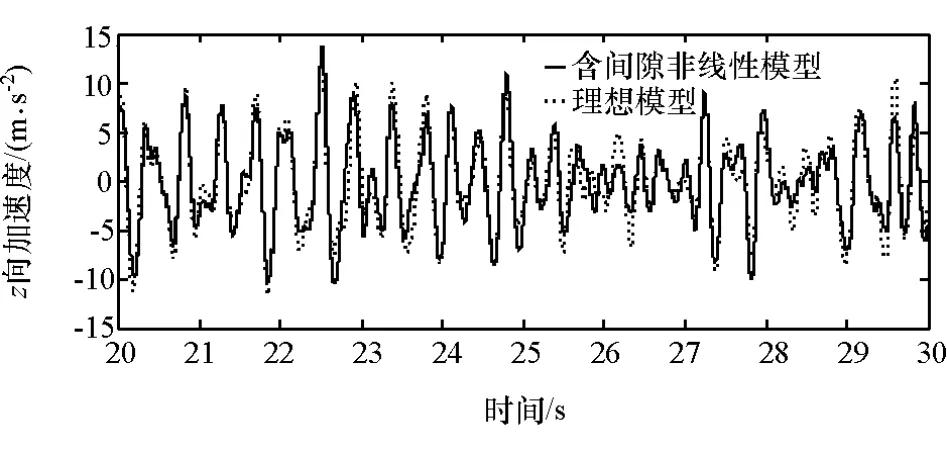
图6 驾驶员时域加速度动态特性

由图6可见，与理想模型相比，当考虑多轴重型汽车平衡轴配合间隙的非线性模型时，驾驶员的加速度特性变化趋势不变，主要差异表现在加速度的变化率方向发生变化的时刻，在大部分时间内，非线性模型加速度的振幅要大于理想模型，表明非线性结构会使车身振动加剧。

4 结论

本文中分析了三轴重型货车平衡轴总成的工作机制，基于摩擦学理论，提出了适用于悬架系统的运动学模型，并代入整车系统中实现了动力学仿真，通过这一应用实例得到以下结论。

(1)通过D级路面激励，得到了车身各自由度和驾驶员的动态特性曲线，为后续研究提供原始数据，如平顺性分析、零部件载荷分析及各零部件的动载荷系数的计算等，还可为汽车弹簧和阻尼器设计提供依据。

(2)通过与理想模型加速度动态特性的对比，突出了平衡轴配合间隙对系统动力学性能的影响，可辅助平衡轴总成的设计。

(3)模型中没有考虑弹性衬套的磨损和变形，实际平衡轴配合间隙要远大于本文中计算数值。平衡轴配合间隙对系统动力学性能的影响要大于本文中分析结果。

(4)本文中初始条件以空载仿真结果为依据，与实际情况有一定的差异，故仿真前0-2s内可能出现振荡情况，但由于阻尼器的存在，振荡的影响很快会消失。