改进希尔伯特-黄变换在电力系统谐波中的应用

李 晨，李 川，姜 飞，张长胜

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

随着电力系统的发展和广泛应用，电能对人们的生产和生活都有不可替代的作用。但是在电力系统中，由于大量电子设备和非线性负载的存在，使相关的电流和电压波形产生较大程度的畸变，即谐波污染[1-3]。近年来，谐波对电网的影响也越来越受到电力部门的重视，国内外的专家、学者均对电力谐波的影响[4-5]、计量[6-7]和抑制[8]进行广泛的研究。1999年，张伏生等人[9]，通过FFT(Fast Fourier Transform，FFT)加窗插值方法提高谐波测量的精度，但都存在一定程度上的频谱泄露和栅栏效应。2012年，房国志等人[10-11]，提出基于FFT和小波包变换的综合检测方法，利用傅里叶变换识别谐波分量，再使用小波包对谐波进行定位和提取，有效的减少了信号提取的运算量，但对于高频信号分辨率较低易造成信号频带混叠现象。

本文针对HHT在进行信号处理时所出现的端点效应问题和模态混叠问题提出了改进方法，采用包络极值延拓法来减少端点“飞冀现象”，通过对原始信号加入白噪声辅助分析来消除模态混叠现象。最后，进行实验仿真。结果表明，改进的希尔伯特-黄变换方法对于暂态扰动信号有更精确的分析和定位。

1 HHT变换原理

希尔伯特-黄变换(Hilbert-Huang Transform，HHT)是1998年Norden E.Huang等人[12]提出的一种经验数据分析方法，并引入Hilbert谱的概念和Hilbert谱的分析方法。HHT是分析非线性非平稳信号的时频分析方法，其中包括两个部分。第一部分为经验模态分解(Empirical Mode Decomposition，EMD)假设任何复杂信号都可以分解为有限数目且具有一定物理定义的固有模态函数(Intrinsic Mode Function，IMF)，并且能够依据信号特点将信号从高到低分解成不同频率的一系列IMF，在自适应获取信号基函数的同时也造成了模态混叠问题。第二部分为Hilbert谱分析(Hilbert Spectrum Analysis，HSA)，将用Hilbert求得的每一阶IMF的瞬时频率和瞬时幅值，既Hilbert谱。IMF需满足两个条件[13-14]：(1) 信号极值点的数量与零点数相等或相差是1；(2) 信号的由极大值定义的上包络和由极小值定义的下包络的局部均值为零，即IMF的上下包络线关于时间轴对称。

1.1 经验模态分解(EMD)

(1) 给定任意信号f(t)，得到信号的极值点(至少两个)，用三次样条插值法分别拟合信号f(t)的极小值和极大值得到上下两条包络线v(t)和u(t)，计算上下两条包络线每点对应的均值mi(t)即mi(t)=[ui(t)+vi(t)]/2；

(2)在每点所对应的fi(t)，用fi(t)减去每点所对应的均值mi(t)得到hi(t)=fi(t)-mi(t)。

用得到的hi(t)检验是否满足IMF的两个条件，若满足则hi(t)为f(t)的第一个IMF即IMF1；若不满足则hi(t)作为原始数据fi(t)重复步骤(1)和(2)得到hij(t)，直到hij(t)满足IMF的两个条件。

(3)将信号f(t)用EMD分解得到的第一个IMF分量c1，r(t)作为新的原始数据得到r(t)=f(t)-c1。

重复步骤(1)、(2)、(3)得到信号f(t)的第2个IMF分量c2，循环n次得到信号f(t)的第n个IMF分量

(1)

式中rn代表函数的平均趋势，是信号的残余分量，其曲线为单调函数或定值。各个IMF分量cn表示了信号的特征尺度，体现非线性非平稳信号的内在模态特征。

1.2 Hilbert谱分析(HSA)

将式(1)中信号的IMF分量ci做希尔伯特谱变换

(2)

得到信号f(t)的解析信号Yi(t)=ci(t)+jHi(t)，由此得到瞬时频率、瞬时相位和瞬时振幅为

(3)

(4)

(5)

所以f(t)的解析信号可表示为

Yi(t)=ci(t)+jHi(t)=ai(t)ejφi(t)=ai(t)ejʃφidt

(6)

以上公式表示了信号f(t)频率、相位和幅值之间的关系。信号f(t)的幅值可以用时间和频率的函数H(ω,t)表示

(7)

对时间进行积分即可得到信号的边际谱

(8)

其中，H(ω,t)是对整个信号的幅值在频率上随时间变化规律的描述；而h(ω)是信号在频率上的总振幅(总能量)。

2 HHT在电力谐波中的应用

基于实际电网中谐波源的不断变化，造成谐波信号的次数、幅值也随之变化。本文采用高次衰减电压突变谐波信号模型f(t)[15-16]。

f(t)=

(9)

其中，设采样频率为3 200 Hz，采样点数N=2 048。在采样周期内，3次谐波在0.06 s处开始衰减幅值由217 V降到87 V，在0.14 s的时候恢复到217 V；9次谐波在0.16 s处开始衰减幅值由93 V降到56 V，在0.24 s恢复到93 V。原始信号波形及其频谱图如图1所示。

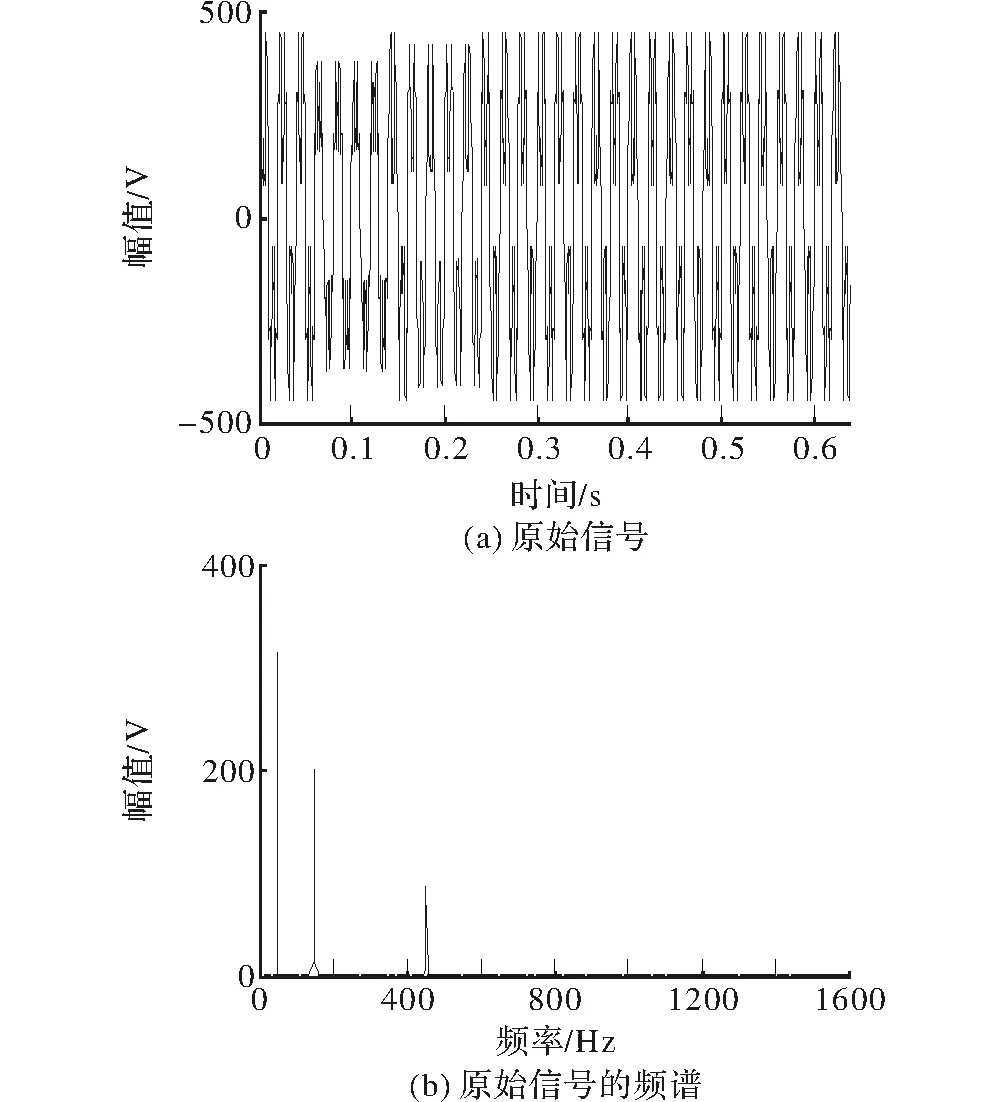
图1 原始信号波形及频谱图

由图1信号的频谱图可知，原始信号中分别包含频率为50 Hz、150 Hz、和450 Hz的基波、3次谐波和9次谐波。

2.1 模态混叠

对信号进行EMD实际就是把信号的频率从高到低的一个分解过程。在分解过程中由于基波幅值分量远大于谐波幅值分量，可能会产生尺度交叉现象，其结果会导致模态混叠现象。如图2所示。

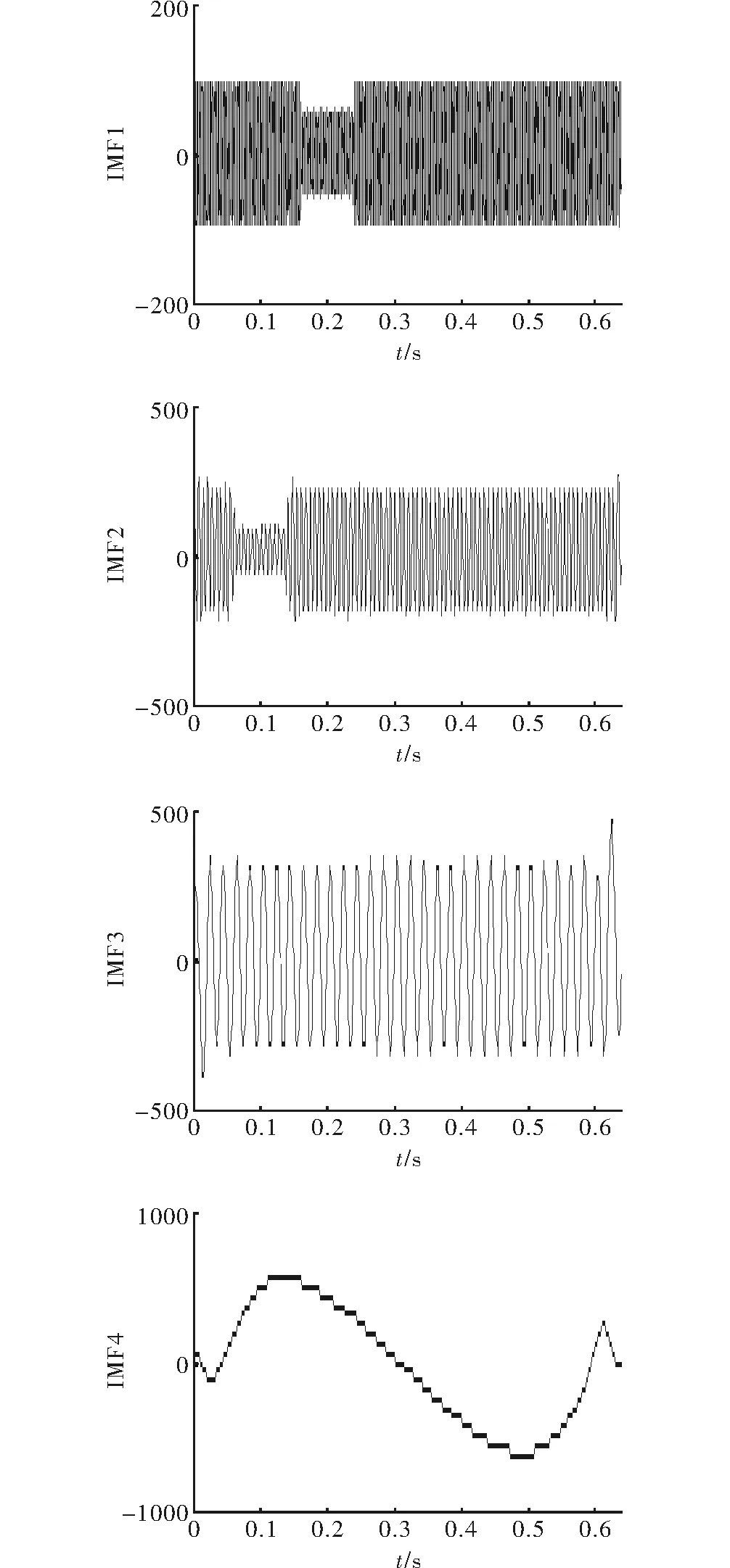
图2 原始信号的EMD分解

由图2可以看出，对原始信号进行EMD分解，生成各个IMF分量，其中IMF1的波形在0.16 s时产生了压降在0.24 s时恢复，IMF2波形在0.06 s时，9次谐波衰减至3次谐波，在0.16 s时恢复。IMF3和 IMF4中两端波形都有变形，在下面IMF的幅频曲线图中更直观的表现出。

2.2 端点效应

对原始信号进行EMD分解后所得到的IMF分量进行Hilbert谱分析时，无法保证端点恰好为极值点。如果在进行Hilbert谱分析时把端点当作极值点处理，则在两端会造成信号的失真，出现明显的“飞冀”现象。可在IMF的瞬时频谱图中清晰的看出，如图3所示。

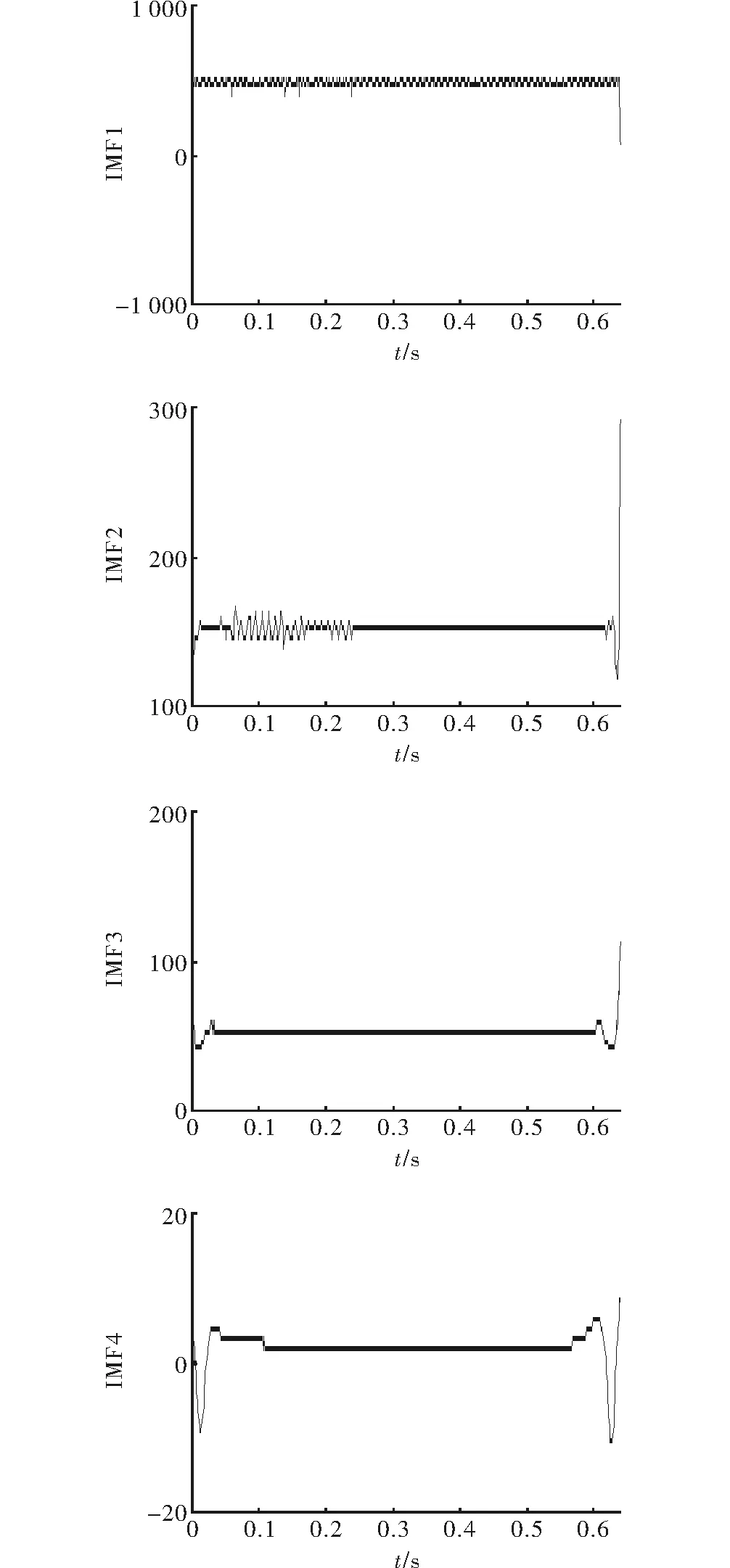
图3 各个IMF的瞬时频率

3 改进HHT的仿真分析

3.1 包络极值延拓法

通过包络极值延拓法来消除分解过程中出现的端点“飞冀”现象。在分解IMF分量时，信号的极值点分别构成上包络线和下包络线。因此为了消除端点现象，依据极值点包络线的特征分别向左右两端进行延拓，同时考虑IMF所需要满足的两个条件，所以分别向左右两端延拓两个极值点。

设有一组信号数据X(T)，其中X(T)中有m个极大值点，有n个极小值点，采样周期为Ts，采样点数为N。

左延拓：设左端的第一个包络波形特征值为l1

(10)

得向左延拓极值的位置和数值分别为

Tm0=Tm1-l1T;Xm(0)=Xm(1)

(11)

Tm-1=Tm1-2l1Ts;Xm(-1)=Xn(1)

(12)

Tn0=Tn1-l1Ts;Xn(0)=Xn(1)

(13)

Tm0=Tm1-2l1Ts;Xn(-1)=Xn(1)

(14)

右延拓：设右端的第一个包络波形特征值为l2

(15)

得向右延拓极值的位置和数值分别为

Tm+1=Tm+l2Ts;Xm(m+1)=Xm(m)

(16)

Tm+2=Tm+2l2Ts;Xm(m+2)=Xm(m)

(17)

Tn+1=Tn+l2Ts;Xn(n+1)=Xn(n)

(18)

Tn+2=Tm+2l2Ts;Xn(n+2)=Xn(n)

(19)

当左右两端的函数值小于邻近端点的极值时，为防止极值在包络线以外，需对其进行特殊处理

Tm0=T1,Xm(0)=X(1);X(1)>Xm(1)

(20)

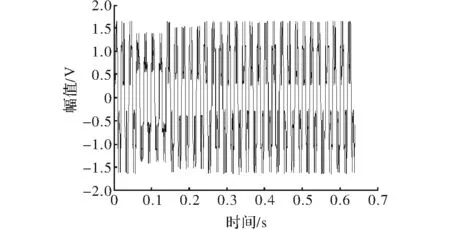
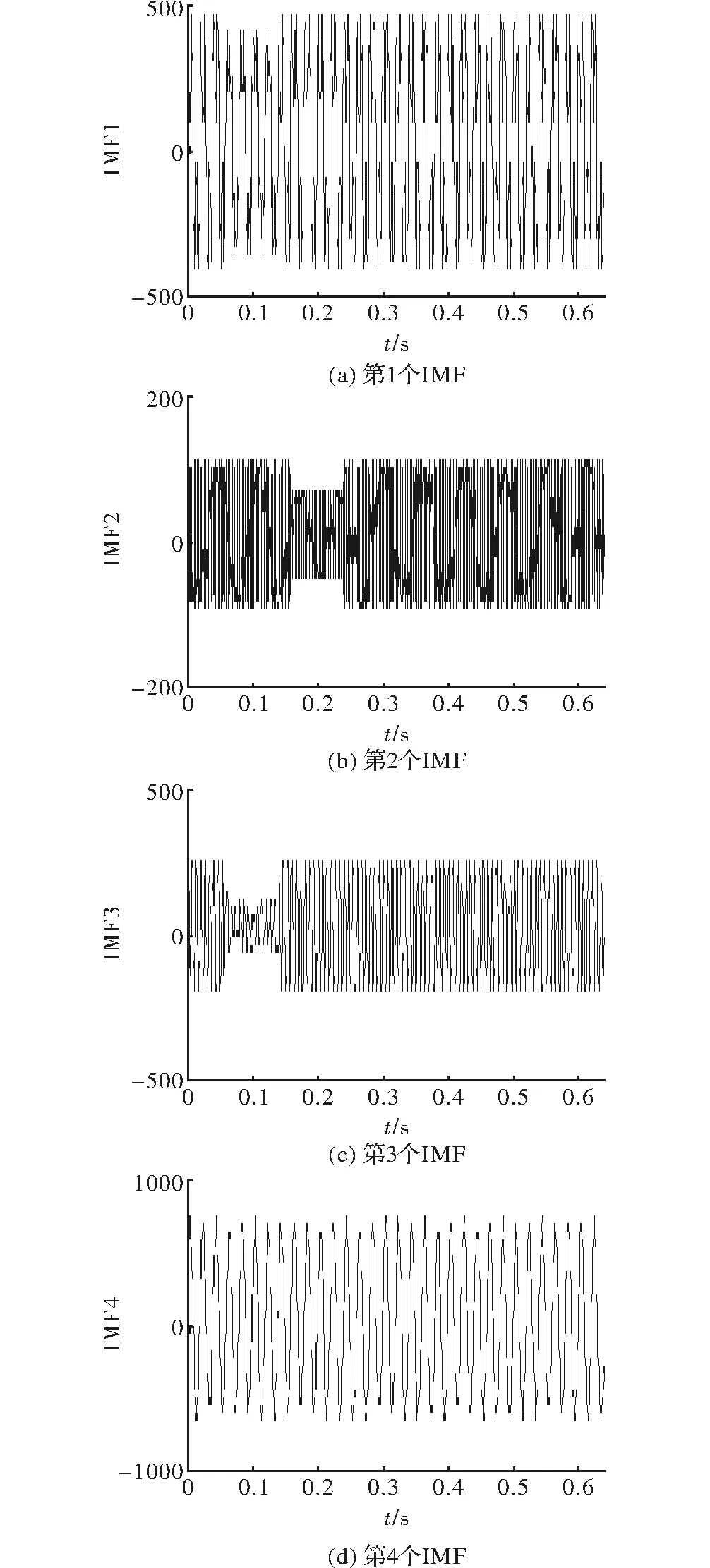
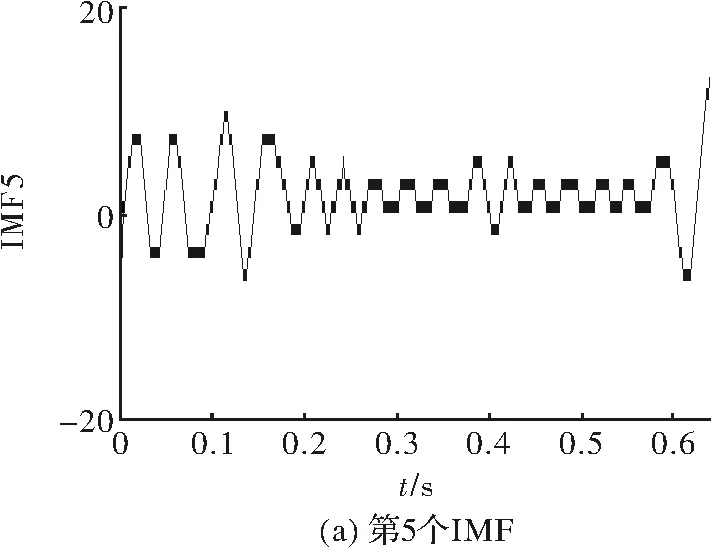
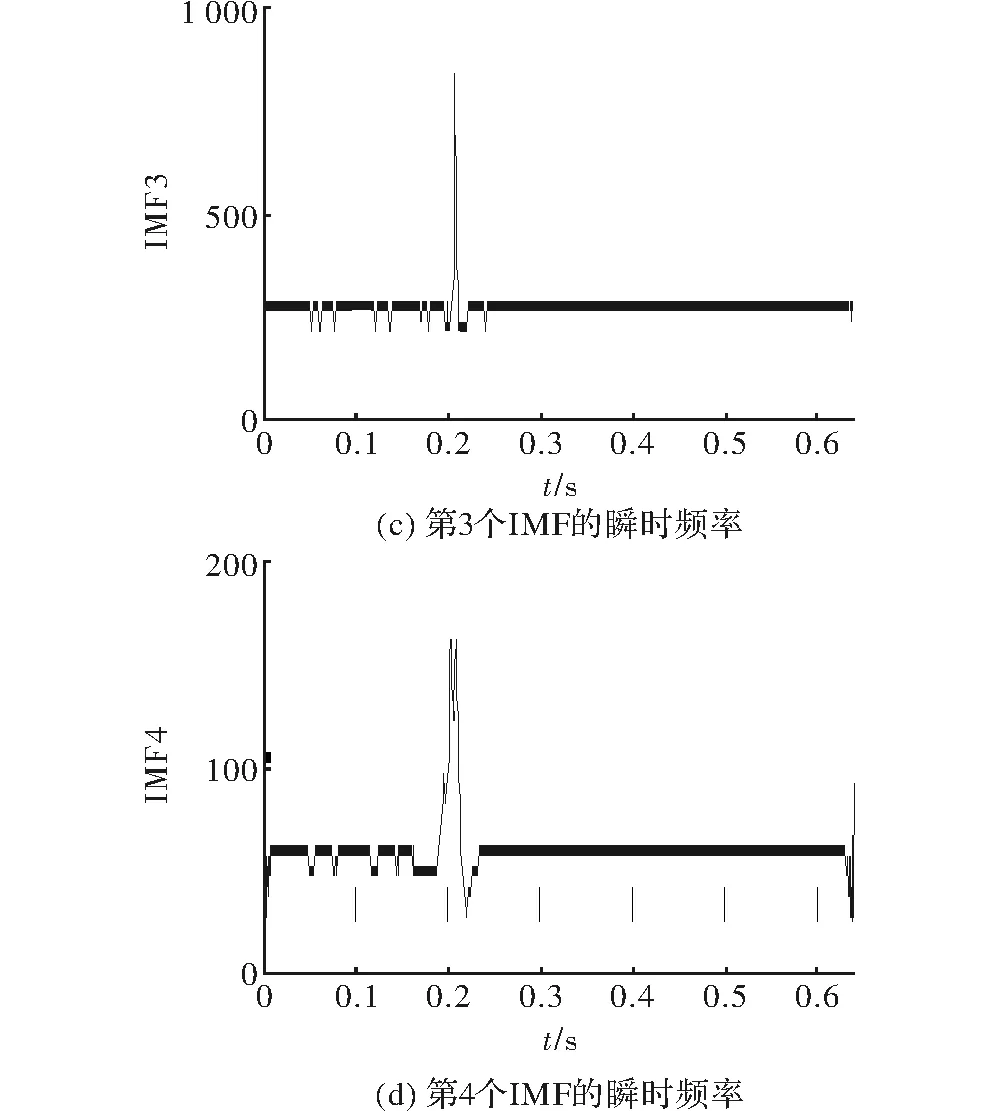
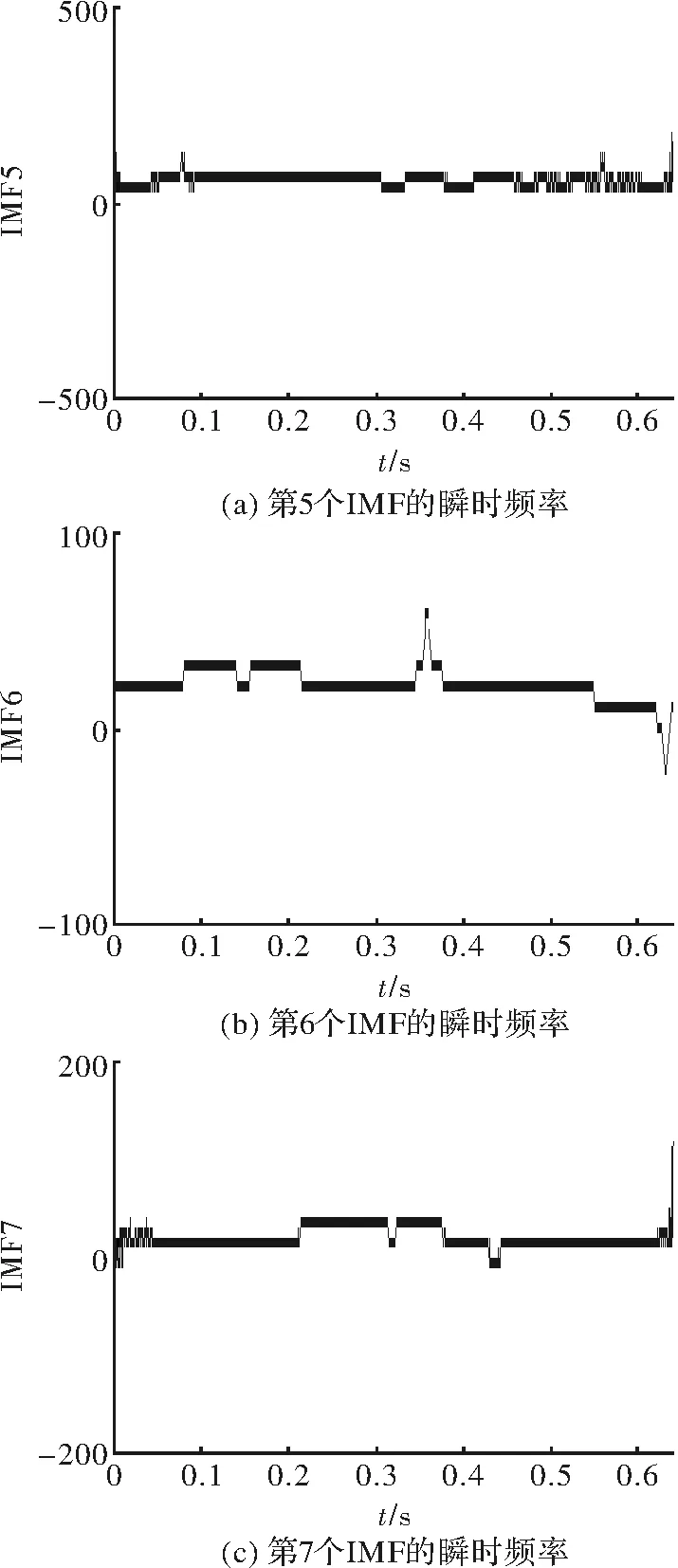
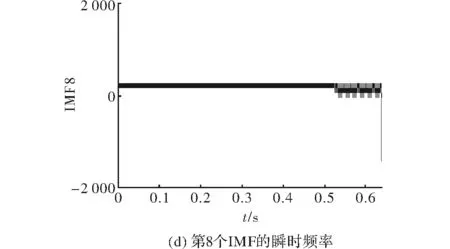
Tn0=T1,Xn(0)=X(1);X(1)

(21)

Tm+1=Tn,Xm(n+1)=X(n);X(n)>Xm(m)

(22)

Tn+1=Tn,Xn(n+1)=X(n);X(n)

(23)

由于分别向左右延拓了4个极值点，最后在进行EMD分解时可以左右两边各去掉几个采样点数以消除延拓对实际信号的影响。

3.2 平均经验模态法

分解时产生的模态混叠现象一方面是和EMD算法有关，另一方面也和原始信号的频率特征有关。当原始信号的时间尺度存在阶跃性变化时，则分解的IMF分量包含不同时间尺度特征分量。针对这一现象，本文采用平均经验模态法来抑制模态混叠现象。在进行EMD分解时相当于一个二阶滤波器组，当信号出现间断点等情况时滤波器无法对信号准确分解。因此采用EEMD方法对信号进行噪声辅助分析，噪声辅助信号方法就是在原始信号中加入白噪声来平滑脉冲干扰，而加入的白噪声对各个固有模态分量的分解并没有影响。白噪声的频谱均匀散落在信号整个时频空间上，由于EEMD能够自适应对信号进行分解，所以不同时间特征的信号会自适应的分布到合适的时间尺度上。并且由于加入的白噪声具有零均值噪声的特性，所以各个固有模态分量在经过多次平均后可消除白噪声。

3.3 改进HHT的仿真

采用改进的HHT算法对式(9)信号模型仿真进行对比。图4为原始信号中加入均值为0、方差为1时正态分布的随机数。

图4 原始信号加噪声

对加入随机白噪声的原始信号进行EEMD分解得到的各个IMF分量，由图5和图6可以看出加入的随机白噪声被很好的分解出来，原始信号中的高次衰减电压突变也得到了很好的处理，IMF2是加入的噪声的余量，其中IMF8的波形接近正弦波形。

图5 信号的IMF1-IMF4分量

图6 信号的IMF5～IMF8分量

图7 信号的IMF1～IMF4的瞬时频率

图8 信号IMF5～IMF8的瞬时频率

由图7和图8可以观察到，在曲线的两端端点“飞冀”问题，可通过包络极值延拓法得到良好的抑制。

4 结束语

本文针对希尔伯特-黄算法在电能谐波分析中出现的端点效应和模态混叠问题，提出用包络极值延拓法和平均经验模态法来改善。利用Matlab建立一个高次衰减电压突变的典型谐波信号模型，对该模型进行仿真。通过改进前后的希尔伯特-黄算法，比较经验模态分解得到的各个IMF分量及其幅频曲线，改进后的希尔伯特-黄算法明显改善了端点效应和模态混叠问题。