基于阻抗边界法的变压器杂散损耗计算与分析

赵 志 刚， 郭 莹， 魏 鹏， 刘 佳， 尹 赛 宁， 杨 凯

(河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室， 天津 300132 )

0 引 言

随着特高压输电系统的迅速发展，变压器的电压等级和安装容量不断提高，变压器的漏磁场强度逐渐增加.漏磁场进入变压器油箱、铁心拉板、铁心夹件等结构件中，导致变压器杂散损耗值增加，对大型电力变压器而言，杂散损耗占据了总损耗的30%～40%，成为变压器损耗中举足轻重的部分.此外，杂散损耗的增加，可能引起不能允许的局部过热，使变压器的使用寿命降低，影响变压器的传输效率和安全稳定运行，对电网造成不可逆的影响[1-5].因此，研发人员从变压器的结构、工艺和材料等方面对变压器进行改进，达到降低漏磁场强度的目的.有效改进变压器性能的根本在于研究和分析漏磁场和杂散损耗的分布规律，从而寻找出可降低结构件漏磁的优化设计方案.

对于电气工程中的杂散损耗问题，在实验研究和数值仿真中都是一个复杂的经典难.在实验研究方面，杂散损耗总是和其他损耗混合在一起，很难将构件中的杂散损耗从总损耗中分离开来[6].传统变压器结构件杂散损耗测量，普遍采用负载损耗总测量值减去空载绕组损耗测量值的方法，其中负载损耗总测量值为绕组损耗与结构件损耗之和[7-8]，该方法忽略了结构件对漏磁场的影响.近些年来，国内学者对传统方法进行了改进，提出了一种测量与仿真结合法，即负载损耗总测量值减去负载绕组损耗计算值，从而可得到变压器结构件的杂散损耗[9-10]，尽管在传统测量方法上有所改进，但却忽略了温度的影响.在仿真计算方面，大多采用有限元方法对其计算，为满足精度要求，需考虑集肤效应等因素，对其进行剖分和分层设置，设置过于精细，会导致仿真时间长，计算成本增加，并不适合工程应用.

本文基于P21-B模型，利用电磁场数值计算软件MagNet，引入一个温度系数因子，提出一种改进的测量与仿真结合法；此外对于计算变压器结构件上的杂散损耗，分别采用传统有限元法和有限元与阻抗边界结合法对模型进行仿真计算，对两种方法得到的结果进行对比，并分析各自的优缺点.

1 实验模型与原理

1.1 实验模型

TEAM Problem 21是以变压器油箱、构件中的杂散损耗问题为研究背景的[7].本文基于P21-B模型对工频(50 Hz)激励电流下导磁钢板中的杂散损耗进行研究.

P21-B模型示意图如图1所示，包含作为激励源的绕组和导磁钢板结构件，其中绕组由2个规格相同、匝数为300匝的导线反向绕制而成，本研究为增大漏磁场强度，两绕组施加反向激励电流；导磁钢板牌号为Q235B，规格为520 mm×360 mm×10 mm.

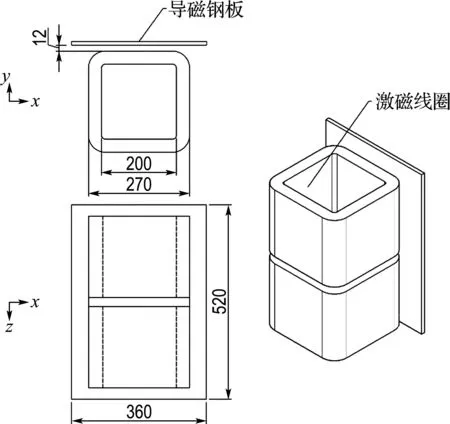
图1 P21-B模型示意图

1.2 实验原理

1.2.1 结构件杂散损耗测量方法

(1)传统测量方法

变压器结构件中的杂散损耗，传统计算方法如下式所示：

Pm-str=Pm-load-Pm-no

(1)

式中：Pm-str为变压器结构件中的杂散损耗，Pm-load是负载损耗总测量值，Pm-no是空载绕组损耗测量值.

而负载条件下，模型的损耗总测量值可表示为

Pm-load=Pm-str+Pm-coil

(2)

式中：Pm-coil为负载绕组损耗测量值.

由于导磁钢板磁导率远大于空气磁导率，在负载工况下，导磁钢板结构件加入，定会导致空间漏磁场的分布改变，造成负载和空载绕组损耗值的不一致，即Pm-no≠Pm-coil，从而影响变压器结构件中杂散损耗的准确分离[8-9].

(2)测量与仿真结合法

针对上述变压器结构件中杂散损耗测量问题，国内学者已提出了一种测量与仿真结合法，如下式所示：

Pm-str=Pm-load-Pc(20)-coil

(3)

式中：Pc(20)-coil为标准温度20 ℃下，负载绕组损耗计算值.

(3)改进的测量与仿真结合法

现有的一些电磁场数值计算软件，给定的材料属性都为标准温度20 ℃时的参数值.因此，软件后处理所得到的绕组损耗计算结果也为标准温度下的绕组损耗计算值.绕组由铜线绕制而成，受温度影响严重，本文引入温度系数因子[11]，对绕组损耗计算值进行修正，如下式所示：

(4)

式中：Pc-coil为实际温度下，负载绕组损耗计算的折算值；θ为绕组实际温度.

Pm-str=Pm-load-Pc-coil

(5)

综合式(4)和(5)，变压器杂散损耗的测量值表示为

(6)

1.2.2 阻抗边界法 阻抗边界法是基于电磁波理论，将导体阻抗边界作为一种边界条件进行有限元求解的方法.由于导磁钢板结构件中的漏磁场透入深度非常小，可忽略导体内的反射波；其透入深度远小于箱壳或结构件的厚度，保证导磁钢板平面仅有法向磁通发生变化，符合阻抗边界法的适用条件[12-13].

变压器油箱的广义波动方程可表示为

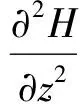
(7)

结合电磁场基本方程

▽×H=σE

(8)

可得关于E的方程：

(9)

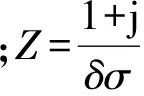
2 测量与仿真

2.1 空载绕组损耗计算

本文基于P21绕组模型，采用整体建模和扁导线精细建模两种方式，如表1所示，对工频激励下的绕组损耗进行研究，以寻求一种可以准确计算变压器绕组损耗的建模方式.

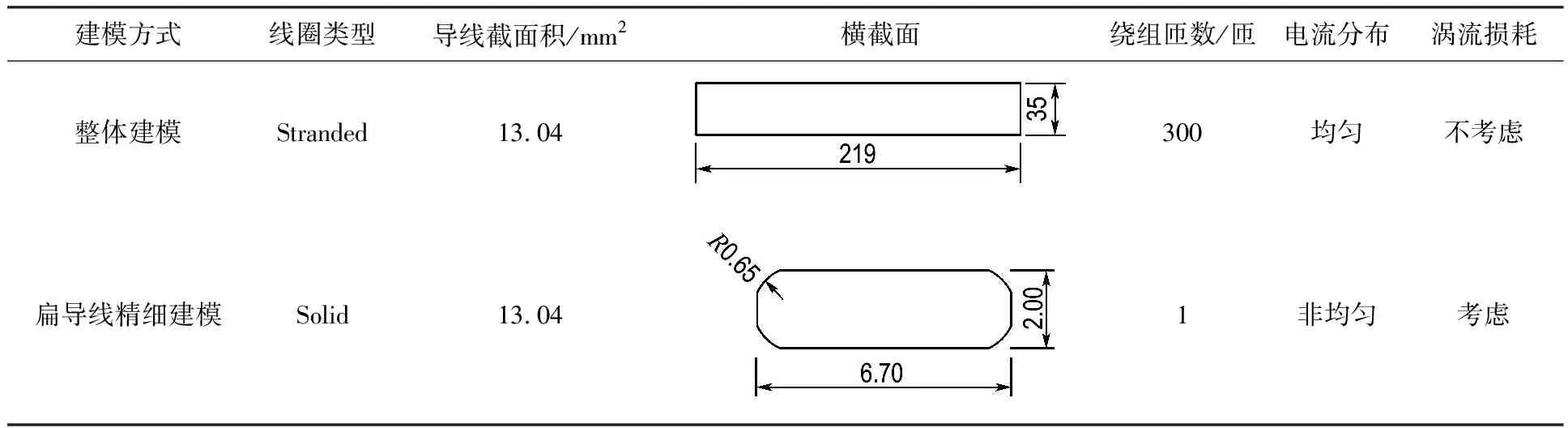
表1 绕组建模方式

整体建模是工程上常用的一种绕组简化建模方式[14-15]，在仿真计算时，仅需设置线圈导线的有效截面积和匝数；而扁导线精细建模，是以实际裸铜线的横截面为构造面进行建模的.两种绕组计算模型如图2所示.

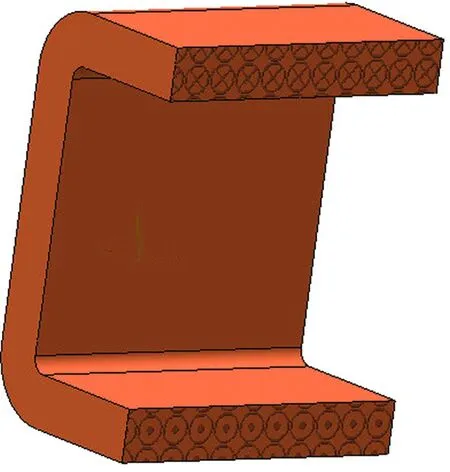
(a) 整体建模

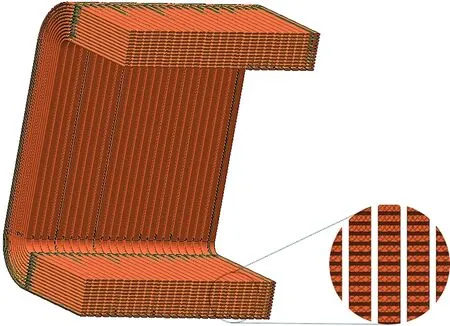
(b) 扁导线精细建模

本文运用三相柱式调压器对工频激励电流下绕组损耗进行测量和仿真计算，所得结果如图3所示.

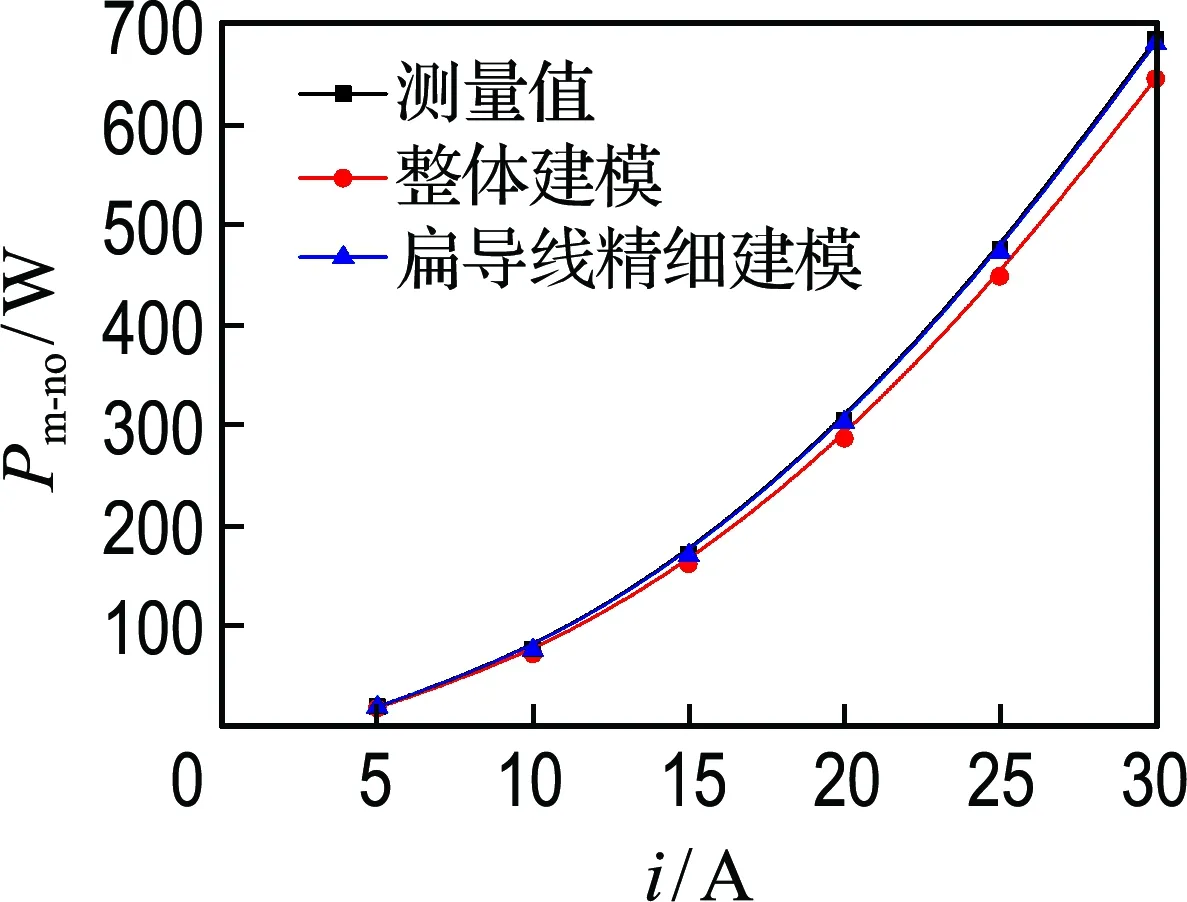
图3 不同激励电流下空载绕组损耗结果

可以得出，传统简化建模由于忽略绕组涡流损耗等影响因素，和实际线圈绕组测量值存在一定误差；而扁导线精细建模，考虑了绕组的涡流损耗和集肤效应影响，与实际测量结果较为吻合.

2.2 负载绕组损耗计算

综上对空载绕组损耗的计算分析，为得到准确的负载绕组损耗计算值，需采用扁导线精细建模方式.为验证负载工况下建模方式的有效性，采用F.W.Bell公司的高斯计(Model 8010 Gaussmeter)对导磁钢板表面(空气中)的法向漏磁通密度进行了测量，如图4所示，沿绕组轴线方向(z方向)共设有25个测试点，高斯计探头厚度为1.52 mm，霍尔元件中心为0.76 mm，因此测量点位于结构件上表面0.76 mm处(x=-0.76 mm).本文对图4所示位置处的磁通密度进行比较，所得不同激励下的磁通密度分布如图5所示.

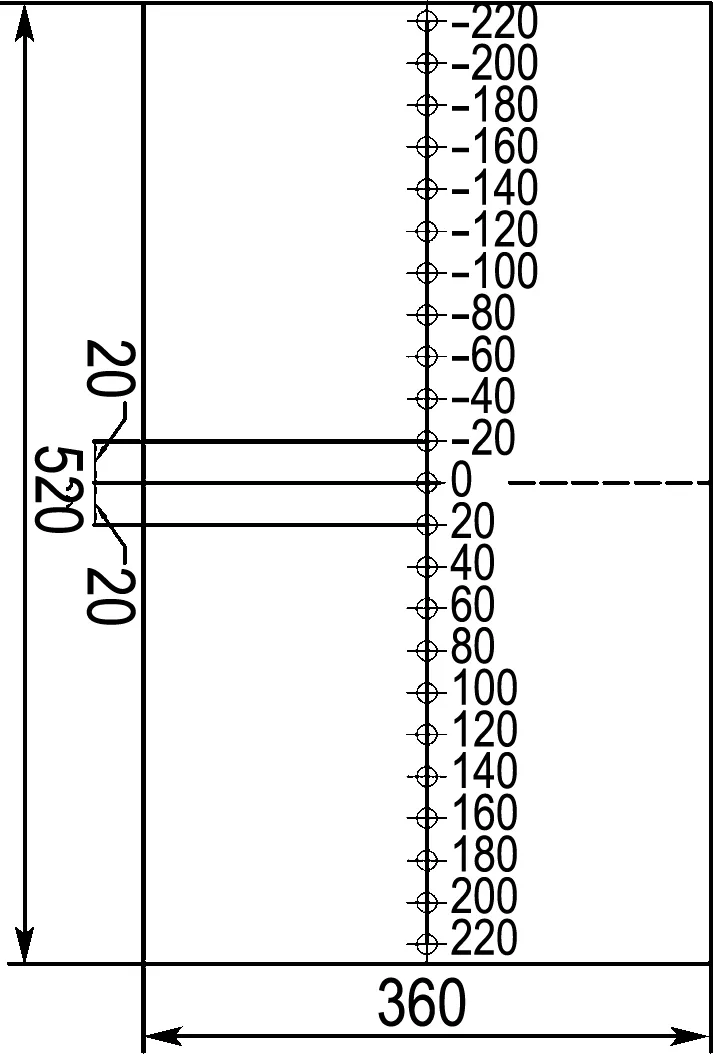
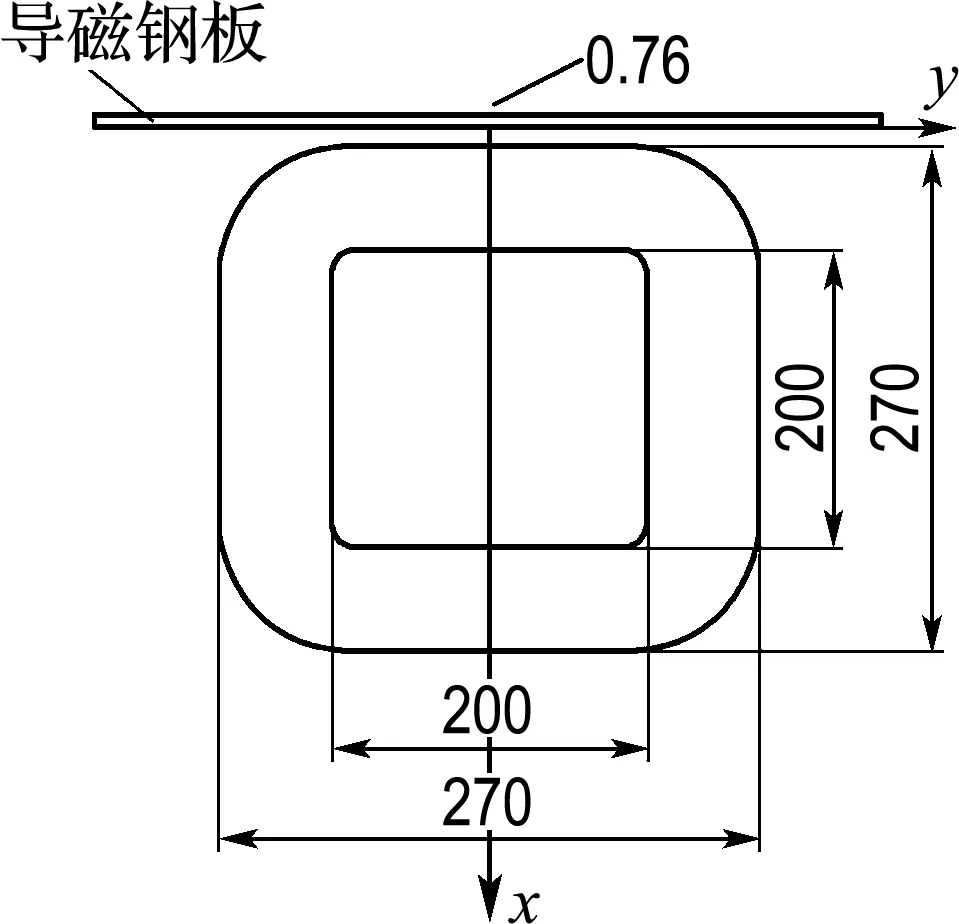
图4 导磁钢板磁通分布测量点

由图5可以看出：导磁钢板表面处的磁通密度分布测量值和计算值近似相等，验证了建模的有效性，从而得到准确的负载绕组损耗计算值，为测量与仿真结合法提供了数据支持.

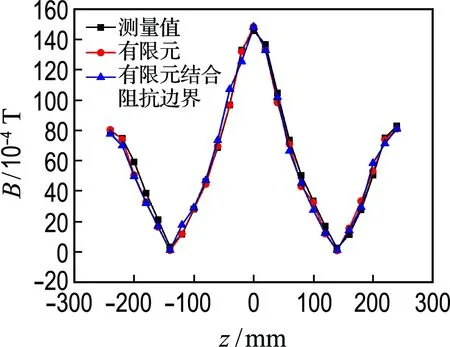
(a) 10 A

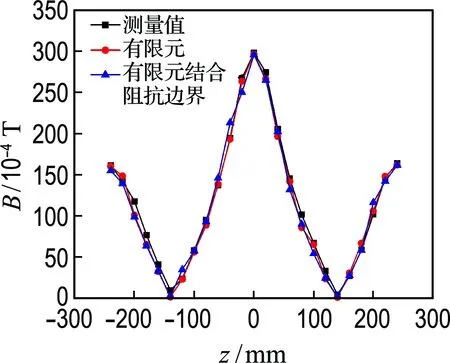
(b) 20 A

图5 导磁钢板空间磁通密度分布(x=-0.76 mm)

Fig.5 Magnetic flux density distribution in magnetic steel plate (x=-0.76 mm)

2.3 导磁钢板结构件损耗

本文分别采用传统测量法、测量与仿真结合法(MEA+SIM)以及改进的测量与仿真结合法(改进MEA+SIM)对变压器导磁钢板结构件进行测量，所得结果如表2所示.通过对数据的对比分析，发现采用测量与仿真结合法，相较于传统测量法，测量精度有所提高，但仍存在一定差距，而引入温度系数因子得到的改进的测量与仿真结合法，可以获得更为准确的导磁钢板杂散损耗的测量结果，因此，本文采用改进的测量与仿真结合法作为实验测量值.

对于变压器导磁构件的杂散损耗仿真计算，基于工程电磁场数值计算软件MagNet，分别采用传统有限元法(FEM)和有限元与阻抗边界结合法(FEM+IB)对模型杂散损耗进行计算，所得结果如表3所示.

由表3分析可得：传统有限元法和有限元与阻抗边界结合法所得损耗结果误差均在4%以内，满足工程所需的精度要求.

本文还对两方法的网格数和求解时间进行了对比，所得数据如表4所示.

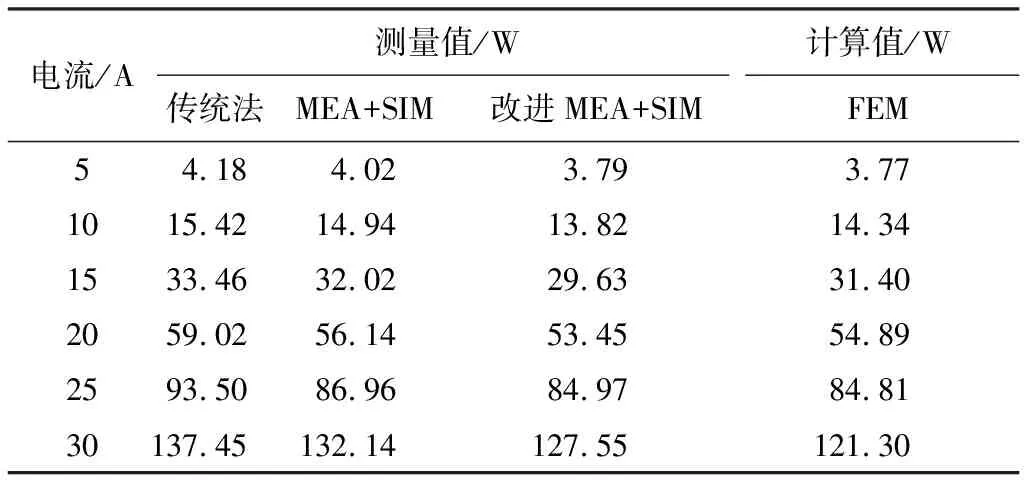
表2 导磁钢板杂散损耗测量值

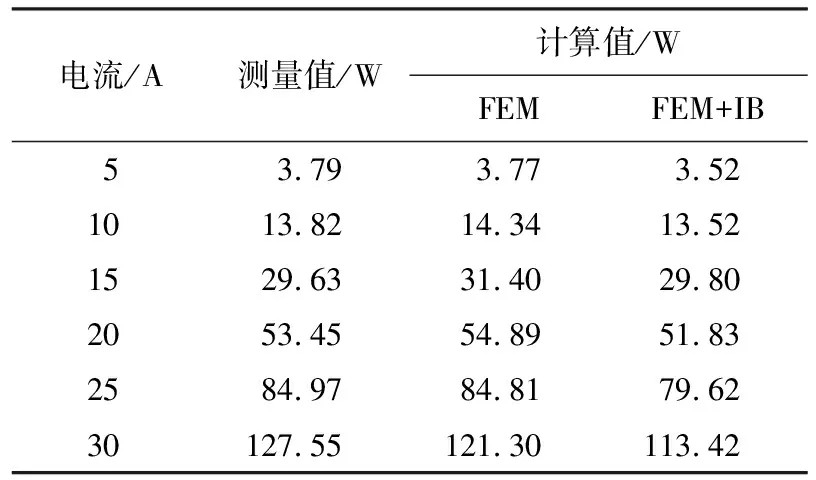
表3 导磁钢板杂散损耗计算值

表4 网格剖分数与求解时间

通过表4对比发现，传统有限元法为保证求解结果的准确性，需要对模型进行分层加密处理，网格数较多，而有限元与阻抗边界结合法不需对结构件进行分层剖分处理，不受频率和集肤效应的影响，操作较为简单，并可减少70%～80%的求解计算时间，减少计算成本，节省计算资源，更适合工程应用.

由图6磁通密度云图对比可以看出，两方法所得到导磁钢板表面的磁通密度分布基本相同，表明采用有限元与阻抗边界结合法计算导磁钢板杂散损耗的有效性.

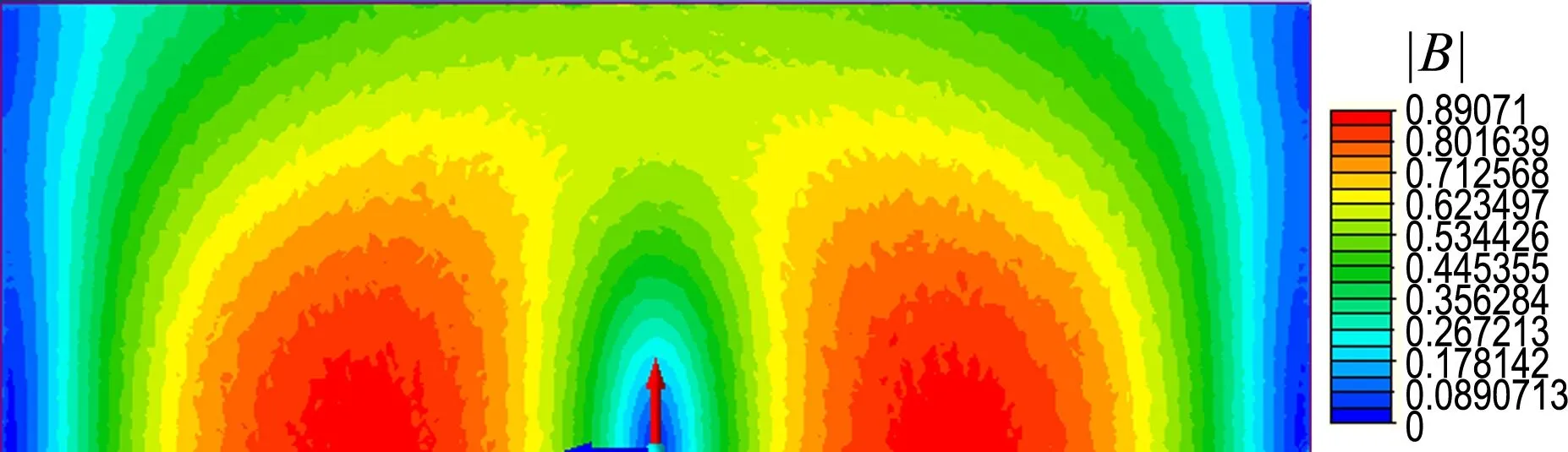
(a) 传统有限元法

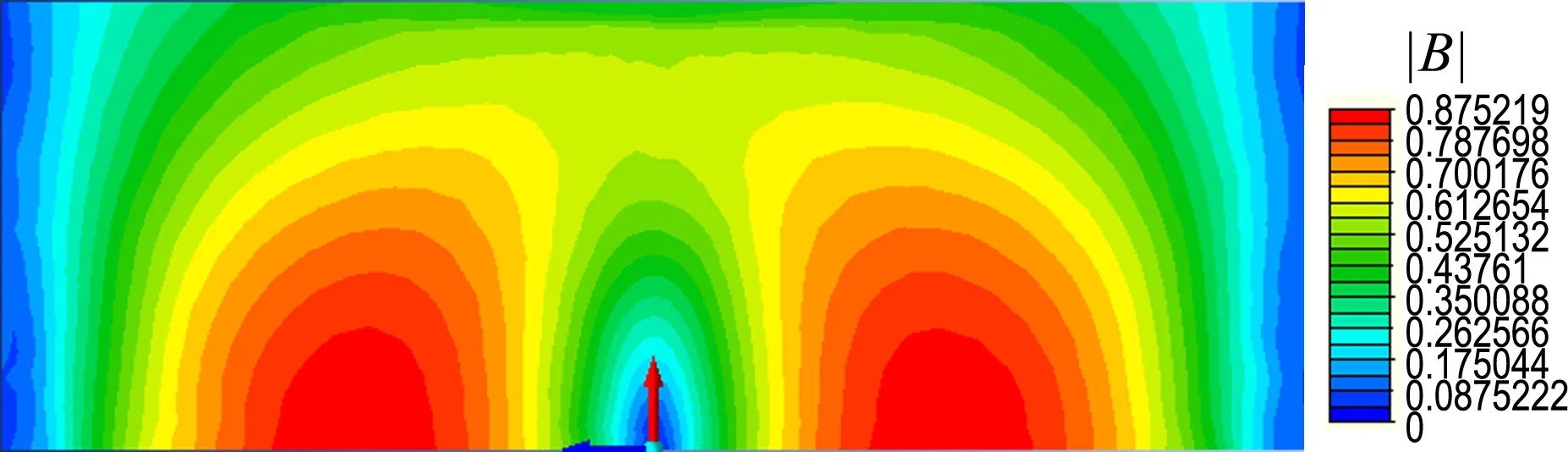
(b) 有限元与阻抗边界结合法

图6 导磁钢板表面磁通密度云图

Fig.6 Shaded plot of magnetic flux density on surface of magnetic steel plate

3 结 论

(1)采用可以考虑绕组涡流损耗和集肤效应的扁导线精细建模方式，能得到更为准确的绕组损耗计算结果.

(2)引入温度系数因子得到改进的测量与仿真结合法，可以获得更为准确的导磁钢板的杂散损耗测量结果.

(3)传统有限元法和有限元与阻抗边界结合法相比，在满足计算精度要求的同时，有限元与阻抗边界结合法可降低有限元网格数，大幅度减少计算成本，节约计算时间，更适合工程应用.