正整数不含分部量2有序分拆的一些恒等式

郭 育 红

(河西学院 数学与统计学院， 甘肃 张掖 734000 )

0 引 言

在整数分拆理论中，MacMahon[1]第一次定义了正整数的有序分拆，即把正整数n表示成一些正整数的有序和，其中每一项叫该分拆的分部量.如果不考虑分部量的顺序就是无序分拆.例如，4的有序分拆有4，3+1，1+3，2+2，2+1+1，1+2+1，1+1+2，1+1+1+1共8个，而4的无序分拆有5个：4，3+1，2+2，2+1+1，1+1+1+1.有序分拆也可以表示成向量的形式.例如，上述4的8个有序分拆可记为(4)，(3 1)，(1 3)，(2 2)，(2 1 1)，(1 2 1)，(1 1 2)，(1 1 1 1).

分拆恒等式一直是分拆理论中很有趣的一部分内容，也一直是分拆理论的研究热点之一.最近几年，许多学者在研究整数分拆恒等式时，不仅考虑正整数不同类型的分拆数之间的关系，比如，在无序分拆的研究中，有Euler恒等式[1-2]以及相关的一系列恒等式.在有序分拆的研究中，关于分部量为奇数的分拆、分部量是1或2的分拆、分部量大于1的分拆之间也有丰富的分拆恒等式[3-5].而且，学者们也考虑了分部量出现的不同类型的频数带来的分拆恒等式.

2015年，Munagi等[6]在有序分拆中考虑了分部量出现的频数问题，给出了关于正整数的In-place有序分拆的几个恒等式.其还将有序分拆的分部量λ给出两种形式，分别表示成λ、λ*.同时将分拆恒等式中偶分部量、奇分部量出现In-place偶数次推广到一般的k次，k≥2，得到了更为宽泛的结果.

所谓正整数的有序分拆中分部量λ出现In-placej次是指在该分拆中，分部量λ连续出现j次.例如，分拆(2 2 2 2 3 4 4 5 5 6 6 2 2 3 1)就是一个偶分部量出现In-place偶数次的有序分拆.

2003年，Chinn等[7]讨论了正整数不含分部量2的有序分拆，给出了一系列计数结果，同时还给出了正整数不含分部量2的有序分拆数的一些组合性质.设正整数不含分部量2的有序分拆数为C≠2(n)，则C≠2(n)满足递推关系：C≠2(0)=C≠2(1)=C≠2(2)=1，C≠2(n)=2C≠2(n-1)-C≠2(n-2)+C≠2(n-3).他们还指出在文献[8]给出的序列中：若用a(n)表示没有孤立的1的二进制序列数，则C≠2(n)=a(n+1)，a(n)的初始值：a(0)=0，a(1)=a(2)=a(3)=1.

本文在文献[6-7]的基础上，探讨正整数n不含分部量2的有序分拆中的In-place恒等式，得到关于分部量1出现In-place偶数次、偶分部量出现In-place偶数次的几个分拆恒等式.同时，研究推广情形.另外，还讨论正整数不含分部量2的有序分拆中，奇分部量有两种形式的分拆数的生成函数及递推关系，并给出递推关系的组合双射证明.

1 已知定理

定理1[9]设n≥1，正整数n的偶分部量出现偶数次的无序分拆数等于正整数n不含分部量≡2(mod 4)的无序分拆数.

定理2[6]设n≥1，正整数n的偶分部量出现In-place偶数次的有序分拆数等于正整数n不含分部量≡2(mod 4)的有序分拆数.

定理3[6]设n≥1，正整数n的奇分部量出现In-place偶数次的有序分拆数等于正整数2n的奇分部量有两种形式的有序分拆数.

2 主要结果

首先给出正整数n不含分部量2的有序分拆中关于分部量1的In-place有序分拆的一个恒等式.

定理4正整数n的不含分部量2的有序分拆中，分部量1出现In-place偶数次(≠0)的分拆数等于n的分部量大于1，且含分部量2的有序分拆数.

反之，对于正整数n的分部量大于1，且含分部量2的有序分拆，将分部量2分拆成(1 1)，其余分部量不变，于是得到n的不含分部量2，且分部量1出现In-place偶数次(≠0)的分拆.

□

例1取n=6，则6的不含分部量2，且分部量1出现In-place偶数次(≠0)的有序分拆有3个：(1 1 4)，(4 1 1)，(1 1 1 1 1 1)；同样，6的分部量大于1，且含分部量2的有序分拆有3个：(2 4)，(4 2)，(2 2 2).

进一步推广定理4，得到下面的结论.

定理5对于正整数l≥2，正整数n的不含分部量l，分部量1出现In-placel的倍数次(≠0)的有序分拆数等于n的分部量大于1，含分部量l的有序分拆数.

证明证法类似于定理4，故略去.

下面给出一个例子来说明该恒等式.

例2取n=10，l=3，则10的不含分部量3，分部量1出现In-place 3的倍数次的有序分拆有11个：(1 1 1 4 1 1 1)，(4 1 1 1 1 1 1)，(1 1 1 1 1 1 4)，(1 1 1 5 2)，(5 1 1 1 2)，(5 2 1 1 1)，(2 5 1 1 1)，(1 1 1 2 5)，(2 1 1 1 5)，(1 1 1 7)，(7 1 1 1).

同样，10的分部量大于1，且含分部量3的有序分拆有以下11个：(3 4 3)，(4 3 3)，(3 3 4)，(3 5 2)，(5 3 2)，(5 2 3)，(2 5 3)，(3 2 5)，(2 3 5)，(3 7)，(7 3).

在定理2、3中，同样考虑正整数n不含分部量2，得到了下面关于In-place有序分拆的两个恒等式.

定理6正整数n的不含分部量2，偶分部量出现In-place偶数次的有序分拆数等于n的不含分部量4，且分部量不是≡2(mod 4)的有序分拆数.

证明类似于Munagi-Sellers在文献[6]中的证法.对于正整数n的任何一个不含分部量4，且分部量不是≡2(mod 4)的有序分拆，做如下变换：将4k型(k>1)的分部量分拆成(2r2r)，这里r>1，其余分部量保持不变.于是，得到正整数n的不含分部量2，偶分部量出现In-place偶数次的有序分拆.反之，在正整数n的不含分部量2，偶分部量出现In-place偶数次的任意一个有序分拆中，奇分部量保持不变，将偶分部量按照从左向右的顺序每两个合并在一起，就得到4k型的分部量，由于分拆不含分部量2，于是就得到n的不含分部量4，且分部量不是≡2(mod 4)的有序分拆.

□

定理7正整数2n的不含分部量4，奇分部量出现In-place偶数次的有序分拆数等于n的不含分部量2，奇分部量有两种形式的有序分拆数.

仍沿用Munagi-Sellers的记号，将奇分部量λ的两种形式记为λ、λ*.

证明类似于Munagi-Sellers在文献[6]中的证法.对于正整数n的任何一个不含分部量2，奇分部量有两种形式的有序分拆，做如下变换：将每个偶分部量μ变成2μ，把没有带*号的奇分部量λ变成2λ，把带*号的奇分部量λ*变换成“λ，λ”.因为n的分拆不含分部量2，于是就得到了正整数2n的不含分部量4，奇分部量出现In-place偶数次的有序分拆.显然，上述变换是可逆的.

□

将定理7做自然的推广，就得到下面的结论：

定理8对于偶数l≥2，正整数2n的不含分部量2l的有序分拆中，奇分部量出现In-place偶数次的分拆数等于n的不含分部量l，奇分部量有两种形式的有序分拆数.

证明证法类似于定理7，故略去.

下面给出一个例子来说明定理8中的对应关系.

例3取n=3，l=2，则6的不含分部量4，奇分部量出现In-place偶数次的有序分拆有10个：(6)，(3 3)，(2 2 2)，(2 2 1 1)，(2 1 1 2)，(1 1 2 2)，(2 1 1 1 1)，(1 1 2 1 1)，(1 1 1 1 2)，(1 1 1 1 1 1).同样，3的不含分部量2，奇分部量有两种形式的有序分拆有以下10个：(3)，(3*)，(1 1 1)，(1 1 1*)，(1 1*1)，(1*1 1)，(1 1*1*)，(1*1 1*)，(1*1*1)，(1*1*1*).

在定理7中涉及正整数n的奇分部量有两种形式的有序分拆数，下面考虑正整数n的不含分部量2，奇分部量有两种形式的有序分拆数.考虑其生成函数.

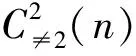
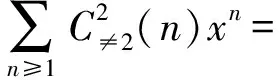
(x4+x6+…))j=

即有下面定理：

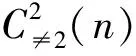
由定理9不难得到下面关于正整数n的不含分部量2，奇分部量有两种形式的有序分拆数的递推关系，有下面的结论.

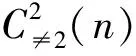
给出该递推关系的组合双射证明.

证明将正整数n的不含分部量2，奇分部量有两种形式的有序分拆分成两类：

(A)右端分部量是1或1*；

(B)右端分部量是t或h*，其中t>2是整数，h>3是奇数.

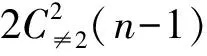
对于(B)类中的任一分拆，用(t-2)或(h-2)*分别代替t或h*，就得到n-2的相应分拆.反之，对于n-2的任一个不含分部量2，奇分部量有两种形式的有序分拆β，设其右端的分部量是r(r≠2)或s*，s是奇数，用(r+2)或(s+2)*分别代替r或s*，就得到n的右端分部量不是1或1*的相应分拆.

□

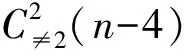
3 结 语

在整数分拆理论中，分拆恒等式的研究一直是研究热点，而对带约束条件正整数有序分拆恒等式的探讨还不是很深入.本文主要研究了正整数n不含分部量2的有序分拆中的分部量1出现In-place偶数次、偶分部量出现In-place偶数次的分拆恒等式，得到了几个有趣的分拆恒等式.另外，还讨论了正整数n不含分部量2的有序分拆中，奇分部量有两种形式的分拆数的生成函数，并给出了该分拆数的递推关系的组合双射证明.这些结果在理论上进一步丰富了整数分拆恒等式，同时也为寻找整数分拆恒等式的组合双射提供了一些方法.