截流钢筋石笼起动流速计算方法研究
2018-07-23汪淼,周宜红,杨忠勇,刘潋,汪庆元,张淑梅
汪 淼, 周 宜 红, 杨 忠 勇, 刘 潋, 汪 庆 元, 张 淑 梅
(1.三峡大学 水利与环境学院, 湖北 宜昌 443002;2.武汉大学 水资源与水电工程科学国家重点实验室, 湖北 武汉 430072;3.长江勘测规划设计研究院, 湖北 武汉 430010 )
0 引 言
截流是标志着水利水电工程进入主体工程施工的重要节点,也是工程建设中至关重要的环节之一,它的成败直接影响着工程的工期和造价.在戗堤合龙时,如何减少抛投料的损失、增加其有效性,是整个截流过程的核心.在一些大型工程截流中,钢筋石笼常常替代了混凝土抛投块体.钢筋石笼制作简单、取材方便,降低了工程成本,同时有着较好的稳定性及透水性,减小了截流难度,发挥了巨大作用.

该公式中的稳定系数K,因包含了拖曳力系数CD、上举力系数CL、摩擦因数f等对块体起动能力有重要影响的因素,导致其取值范围较大、计算结果有一定偏差.
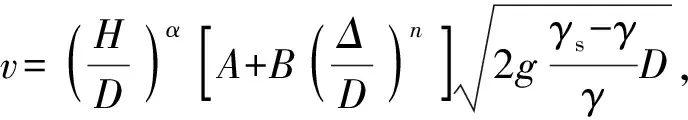
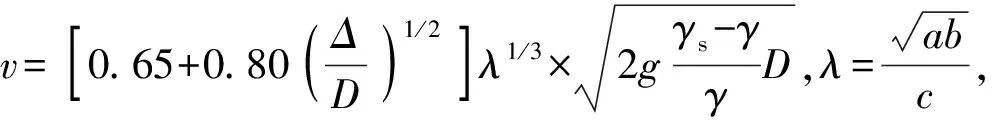

叶恩立所提出的公式较好地解决了采用化引直径D替代钢筋石笼几何尺度以及底部摩擦力的相关问题,但该公式忽略了上举力系数CL对起动流速的影响.对于计算底面积相对较大的钢筋石笼而言,其所受上举力较大,忽略CL会对起动流速的计算造成一定偏差.
针对上述分析,本文从单个截流钢筋石笼的起动机理着手,推导其起动流速计算公式;通过水槽模型试验,得出(λ,Re*,CD)与(λ,Re*,CL)分布云图,提出起动流速计算公式和CD、CL分布云图二者结合的钢筋石笼起动流速计算方法.
1 理论分析
以水体中的单体钢筋石笼为例,其受力如图1所示.Fd为迎水面推力,Fl为上举力,Fz为摩擦阻力,G为钢筋石笼有效重力.

图1 钢筋石笼受力分析
其中,各个力的表达式如下:
(1)
(2)
Fz=f(G-Fl)
(3)
G=(γs-γ)Vs
(4)
Vs=l1l2l3(1-n)
(5)
式中:vd为钢筋石笼高度内的平均流速,Ad为钢筋石笼迎水面面积,Al为钢筋石笼底面面积,Vs为钢筋石笼体积,n为钢筋石笼空隙率.
钢筋石笼起动临界条件为Fd=Fz,即
(6)
由此可知,计算出钢筋石笼起动流速的关键在于能否确定CD、CL的取值.

(7)
为获取CD、CL与λ和Re*的定量关系,文中采用不同尺寸、不同扁度系数的单体钢筋石笼,在3种摩擦因数的基面上进行钢筋石笼起动流速试验,并根据相关数据绘制出(λ,Re*,l1CD+fl3CL)分布云图.通过3幅云图对应的方程求解两个未知数CD、CL,即采用最小二乘法求出最优解,由此绘制(λ,Re*,CD)与(λ,Re*,CL)的分布云图.
2 模型试验及分析
模型试验按1∶50的比尺在有机玻璃水槽中进行.水槽长10 m、宽0.50 m、深0.75 m.试验基面分为有机玻璃基面(f=0.28)、光滑水泥板基面(f=0.48)、粗糙水泥板基面(f=0.69).下列试验成果数值均为原型值.
2.1 试验钢筋石笼规格
查阅实际工程中钢筋石笼规格及相关试验研究[6-7],本文试验块体选用六面体钢筋石笼,分为正六面体钢筋石笼、条形六面体钢筋石笼和扁形六面体钢筋石笼.所有钢筋石笼的容重均为19.60 kN/m3.正六面体钢筋石笼选用不同体积的试验块体,规格如表1所示.
试验采用的条形、扁形六面体钢筋石笼与原型边长为2 m的正六面体钢筋石笼同体积,并以此为参照对象进行尺寸变换,分为两种情况:(1)对于条形六面体钢筋石笼,保持中轴不变,改变长轴与短轴尺寸.(2)对于扁形六面体钢筋石笼,使长轴与中轴同步变化,保持其所在面为正方形,改变短轴尺寸.条形和扁形六面体钢筋石笼规格如表2、3所示.
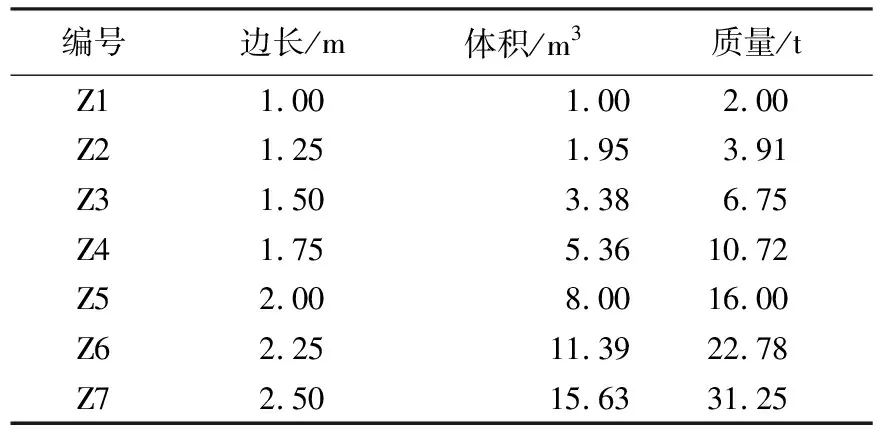
表1 正六面体钢筋石笼规格

表2 条形六面体钢筋石笼规格

表3 扁形六面体钢筋石笼规格
2.2 试验程序
将试验块体放置于水槽中的试验基面,保持来流量不变,通过尾门调节下游水位,直至试验块体开始滑动,且滑动一段又能停止下来,测量钢筋石笼高度内的流速.
试验中对于条形六面体钢筋石笼而言,在水流的作用下,钢筋石笼总是以相对稳定的形式保持自身的稳定.因此,本试验中所有条形六面体钢筋石笼摆放方式均为中轴b与短轴c所在面为迎水面,长轴a沿水流方向,短轴c垂直于试验基面的方式摆放.
2.3 试验成果及分析
在3种不同摩擦因数条件下,经过多次试验,对钢筋石笼所在高度内的流速取平均值,并进行相关试验数据处理.不同规格的单体钢筋石笼起动流速变化规律见图2~4.
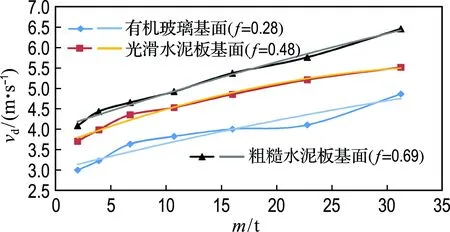
图2 正六面体钢筋石笼起动流速随质量的变化规律
Fig.2 Relationships between incipient velocities and mass of regular hexahedron rock-filled steel cages

图3 条形六面体钢筋石笼起动流速随扁度系数的变化规律
Fig.3 Relationships between incipient velocities and flattening coefficients of bar hexahedron rock-filled steel cages
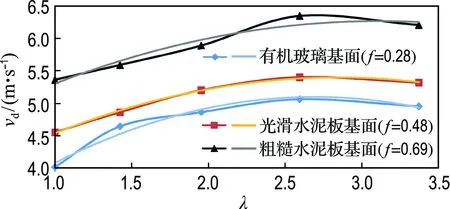
图4 扁形六面体钢筋石笼起动流速随扁度系数的变化规律
Fig.4 Relationships between incipient velocities and flattening coefficients of flat hexahedron rock-filled steel cages
根据图2~4中的变化规律,试验结果表明:(1)在同一摩擦因数条件下,正六面体钢筋石笼的起动流速随着质量的增加而增大;条形六面体钢筋石笼在一定扁度系数λ范围内,随着扁度系数的增加,起动流速增大并趋于稳定;扁形六面体钢筋石笼随着扁度系数λ的增加,起动流速增大,超过一定扁度系数后,起动流速减小.应当注意,扁形六面体钢筋石笼B3、B5之间存在最优扁度系数λ0可使同容重、同体积的钢筋石笼起动流速达到最大.由于本试验所采用模型比尺为1∶50,B3、B4、B5试验块体各边长尺寸已相差甚微,通过制作更多尺寸的钢筋石笼并结合试验验证找出最优扁度系数λ0较为困难,但可知对于扁形六面体钢筋石笼而言,λ0取值范围为1.95<λ0<3.37.(2)在同一摩擦因数条件下,同容重、同体积的条形、扁形六面体钢筋石笼的起动流速比正六面体钢筋石笼起动流速大.(3)底面摩擦因数越大,钢筋石笼的起动流速越大;摩擦因数的改变对钢筋石笼的起动流速有着显著影响,如f=0.48条件下的16 t钢筋石笼起动流速与f=0.28条件下的31.25 t钢筋石笼起动流速相当.
通过对相关数据进行处理,可绘制出3种摩擦因数f=0.28、f=0.48、f=0.69条件下(λ,Re*,l1CD+fl3CL)的分布云图,如图5所示.
在计算CD、CL时,一般采用任意两种摩擦因数条件下的(λ,Re*,l1CD+fl3CL)分布云图,可对CD和CL进行求解,但是为排除两组试验所产生的偶然误差,选用3种摩擦因数的试验数据,能够对所计算的CD、CL取值进行拟合,所得出的值将更加准确.
计算CD和CL所采用的数学方法主要为插值法和最小二乘法.
通过程序编写与计算,利用图5对CD与CL进行求解,绘制出(λ,Re*,CD)与(λ,Re*,CL)的分布云图,如图6、7所示.
由图6、7可知,拖曳力系数CD与上举力系数CL的取值均在0.2~0.6,符合取值范围要求.
CD的取值变化较小,一般在0.2~0.4.随着扁度系数λ的增加,CD的取值呈现下降趋势;部分超过0.4的取值主要集中在扁度系数λ=1、沙粒雷诺数Re*=106.94附近.CD的分布规律也反映出正六面体钢筋石笼所受拖曳力的影响相较于条形、扁形六面体钢筋石笼更为明显,不利于钢筋石笼在水体中的稳定.

(a) 有机玻璃基面(f=0.28)

(b) 光滑水泥板基面(f=0.48)

(c) 粗糙水泥板基面(f=0.69)
图5 (λ,Re*,l1CD+fl3CL)分布
Fig.5 Distribution of (λ,Re*,l1CD+fl3CL)

图6 (λ,Re*,CD)分布

图7 (λ,Re*,CL)分布
CL的取值变化较大,一般在0.2~0.5.在扁度系数λ一定时,随着沙粒雷诺数Re*的增加,CL的取值呈现上升趋势.在Re*一定时,随着λ的增加,且在1.0~1.5,CL的取值基本保持不变;随着λ继续增加,CL的取值呈现下降趋势.结合前文分析可知,当钢筋石笼λ较小时,上举力Fl受上举力系数CL影响相对明显;而当钢筋石笼λ较大时,Fl受钢筋石笼底面面积影响较大.
3 计算方法精度验证

为验证钢筋石笼起动流速计算公式及(λ,Re*,CD)、(λ,Re*,CL)分布云图的精度,采用另一组规格的钢筋石笼在水槽中进行试验.试验基面选取有机玻璃基面(f=0.28),并将计算值与试验值进行对比,对该起动流速计算方法进行精度验证.
验证所用钢筋石笼规格仍选取原型边长为2 m 的正六面体钢筋石笼规格作基准,进行等体积的尺寸变换,保持中轴与短轴同步变化,改变长轴尺寸.验证所采用的钢筋石笼规格如表4所示.

表4 计算方法精度验证所用钢筋石笼规格
根据式(6)及图6、7,得出该组钢筋石笼起动流速计算值vd,绘制vd与对应扁度系数λ的关系曲线,同时绘制试验值曲线,如图8所示.
由图8可看出,验证所采用钢筋石笼的起动流速计算值与试验值基本吻合.
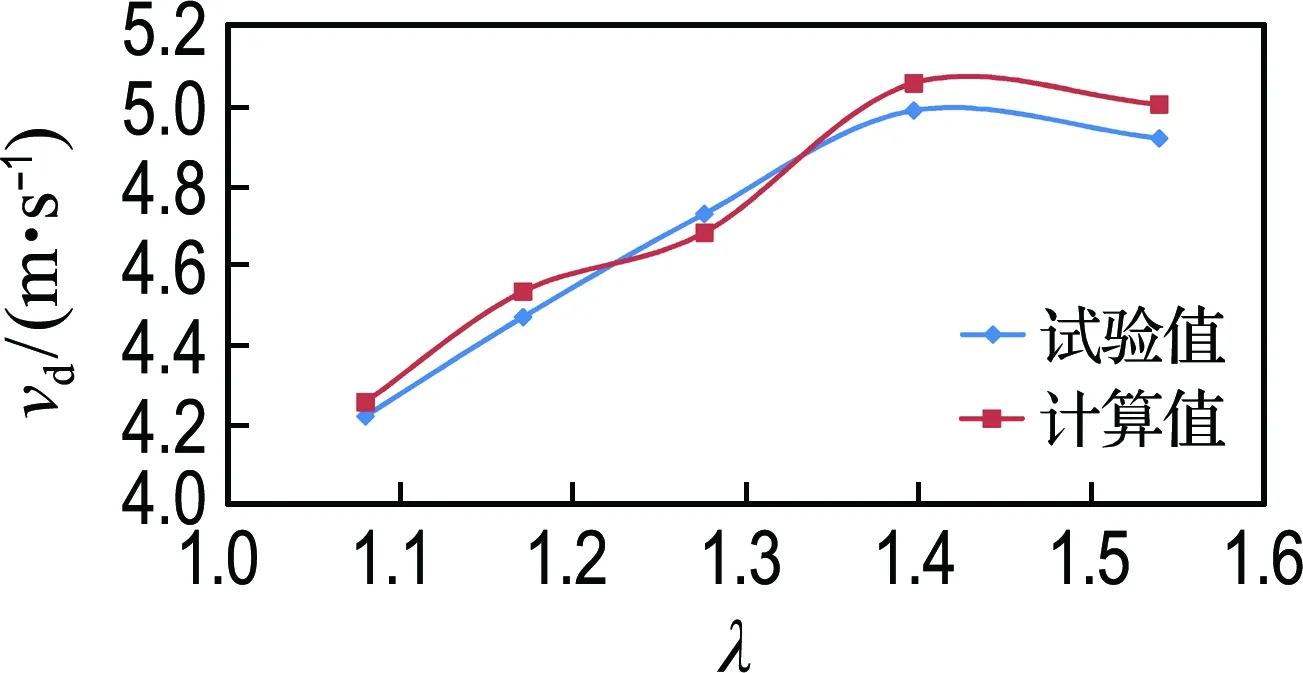
图8 不同规格钢筋石笼起动流速计算值与试验值对比
Fig.8 Comparison between incipient velocities of calculation and test for different sizes of rock-filled steel cages
4 结 论
(1)适当增加钢筋石笼扁度系数有利于钢筋石笼在水体中的稳定,但过度增加其扁度系数将导致钢筋石笼过于扁平,不利于稳定.
(2)底面摩擦因数越大,钢筋石笼的起动流速越大;且摩擦因数的改变对钢筋石笼的起动流速有着显著影响.
(3)拖曳力系数CD的取值一般在0.2~0.4,上举力系数CL的取值一般在0.2~0.5.
