新型箔片动压气体轴承气膜承载力研究
2018-07-23任晓乐董小瑞张学清刘思蓉靳嵘
任晓乐,董小瑞,张学清,刘思蓉,靳嵘
(1.中北大学 能源动力工程学院,太原 030051;2.中国北方发动机研究所,天津 300000)
箔片动压气体轴承由于在一些超高温、超低温等极端环境条件下可保持高速、高精度、无污染等优势,在工业涡轮机械方面引起极大地关注[1]。在箔片动压气体轴承发展的过程中,承载力有限是当前制约轴承向更高转速、更高精度发展的瓶颈。由于箔片结构的变化是影响轴承承载力变化的重要因素之一,研究人员设计了结构多样、形式各异的箔片结构来提高轴承的承载能力[2-3]。箔片动压气体轴承结构地发展以波箔型径向气体轴承地发展最为广泛,其承载力不断提高,但较为成熟的第3代波箔型轴承承载力也只是刚性表面圆轴承承载力的0.85~0.95[4]。
国内外学者对箔片轴承的承载特性进行了大量较为系统的研究。文献[5]分别建立箔片轴承的二维、三维结构研究箔片刚度变化、气弹耦合变形对轴承静态承载力的影响。文献[6]研究了箔片结构阻尼和刚度对轴承承载力的影响,通过设定承载系数,将结构刚度和承载力联系起来建立数值方程,为提高承载力奠定数学基础。文献[7]通过建立定常可压缩Reynolds方程与波箔变形方程等组成的控制方程,采用有限差分法研究不同箔片结构参数对轴承承载特性的影响, 为箔片结构设计提供参考依据。文献[8]通过建立简单的可压缩Reynolds方程和弹性边界变形条件来研究轴承长径比、轴承间隙对轴承承载力的影响。文献[9]研究了分离式波箔型轴承的承载能力,比整体式波箔型轴承的承载能力有很大提升。
现设计一种综合波箔型气体轴承中平箔片和波箔片2种类型的箔片结构,考虑气体的可压缩性,采用FLUENT软件模拟箔片动压轴承的二维、三维流场,得到轴承的气膜压力分布,并计算轴承的承载力。以相同条件下表面为刚性的360°圆轴承的承载压力作为对比,研究新型箔片动压气体轴承的箔片结构参数对承载能力的影响。
1 模型建立与理论分析
1.1 计算模型的建立
典型箔片动压气体轴承主要由轴承外壳、波箔片、平箔片3部分组成[10],其结构如图1所示。波箔片为轴、平箔片提供刚性支承,平箔片为轴承内表面提供柔性支承。

图1 典型箔片动压气体轴承
考虑到典型箔片动压气体轴承中平箔片与波箔片加工条件和安装环境的复杂性,设计一种集合平箔片和波箔片优点的箔片结构。综合波箔片在箔片轴承结构中出现的位置、形状以及各项结构参数,设计3种轴承,结构如图2所示。图2a为覆盖整个圆周表面的波纹箔片与平箔片的耦合箔片,称为全波箔片轴承;图2b为覆盖圆周上表面的波纹箔片与平箔片的耦合箔片,称为上波箔片轴承;图2c为覆盖圆周下表面的波纹箔片与平箔片的耦合箔片,称为下波箔片轴承。

图2 3种轴承结构
波箔片结构的可变参数包括波高、波宽、波数。波高取值为0.1~0.9 mm。箔片轴承的主要参数见表1。

表1 箔片轴承结构参数
1.2 理论分析
对于轴向长度有限的径向气体轴承,将气体连续性方程、动量传递方程、Newton黏性定律以及Reynolds方程联立求解得到可压缩气体的Reynolds方程为[11]559
(1)
式中:p为气膜压力;h为气膜厚度;μ为动力黏度;U为气体沿x方向的速度。
箔片轴承的边界条件设置为
(2)
式中:pa为环境压力。
求解Reynolds方程、计算轴承性能时需对方程进行量纲一化处理,(1)式可化为[12]537
(3)
式中:φ,λ分别为沿轴承周向、轴向量纲一的坐标;H为量纲一的气膜厚度;P为量纲一的气膜压力;Λ为轴承数;ω为转子的角速度。
箔片轴承的气膜承载力为
(4)
式中:Wx,Wy分别为轴承水平、垂直方向上的气膜承载力;θ为转子的偏位角。
2 数值求解
为便于求解,将θ设置为0,轴承的气膜承载力全部设为垂直于水平面的分力。由于润滑气体在一维流动(二维模型)研究中不设置进出口边界,而在二维流动(三维模型)研究中设置进出口边界,导致一维流动与二维流动气膜承载特性有所不同,故将网格划分后的二维、三维模型分别导入FLUENT中计算,并与刚性表面圆轴承的承载力进行比较。网格划分模型如图3所示。

图3 网格划分模型
在FLUENT中进行仿真计算,将环境压力设为常压,气膜流场中的气体设为理想气体。选用基于密度的求解器求解N-S方程与能量方程。轴的转速设为典型工况30 000 r/min,其他边界设为不可滑移的固定边界,表面温度设为27 ℃。
根据Reynolds数的求解方程
(5)
式中:υ为润滑气体的流速,m/s。由此可得:在气膜厚度小于0.802 mm的情况下,Reynolds数小于4 000;而刚性表面圆轴承的气膜厚度最大处为0.038 mm,为保证相同的计算前提,故选用层流模型。求解收敛的标准除能量外设为1×10-4次,并通过监视轴表面压力的变化作为收敛的第2标准。
3 结果与分析
3.1 二维轴承模型气膜承载力
波宽为8°时不同箔片结构的轴承二维承载力对比如图4所示。以刚性表面圆轴承的承载力作为评价基准,由图可知:随着波高的增加,全波箔片轴承与上波箔片轴承的承载力不断减小,并出现承载力为负的情况;下波箔片轴承的承载力增速较快,波高达到0.5 mm以上时,承载力缓慢下降。
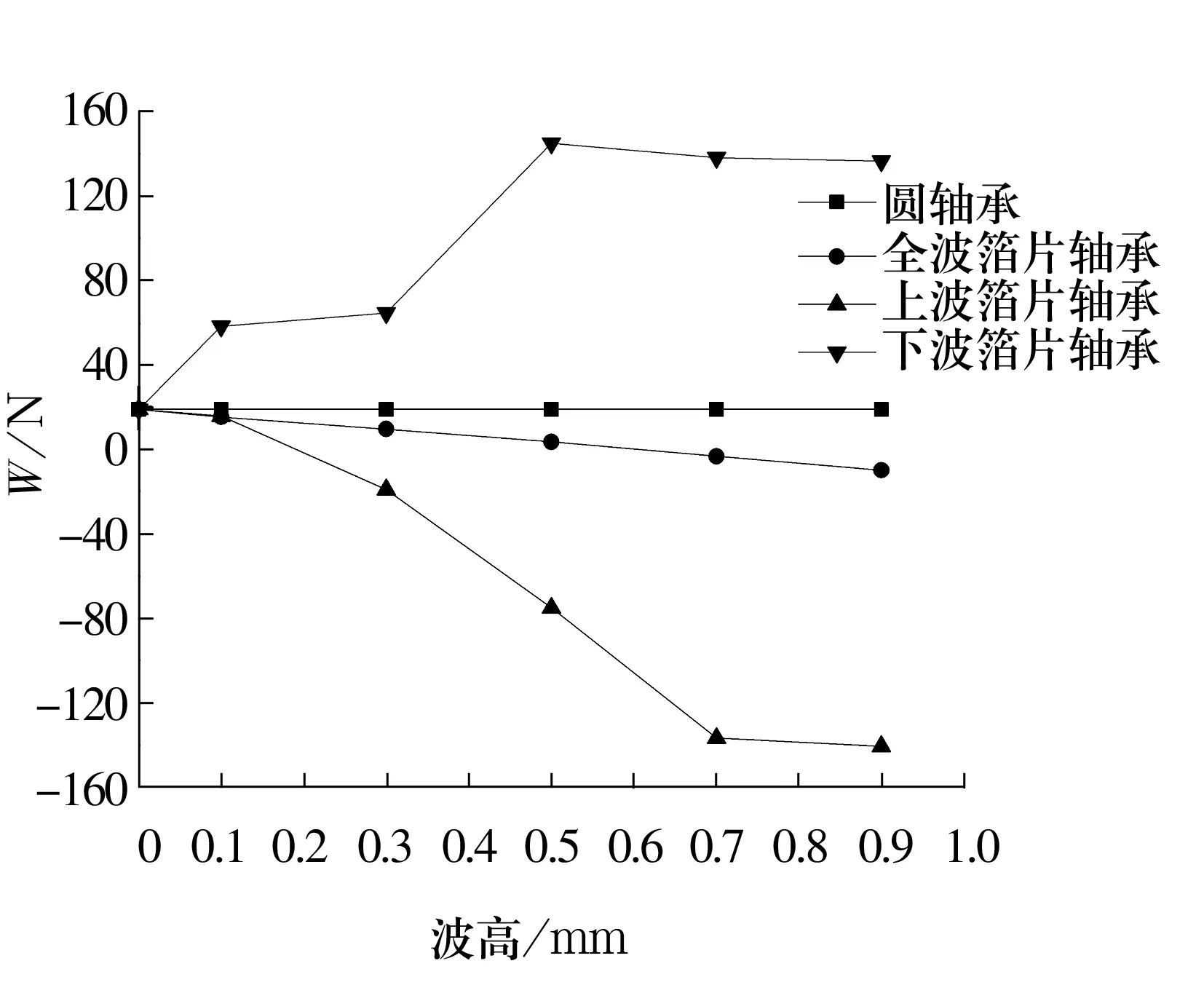
图4 不同轴承的二维承载力对比
上下箔片轴承二维气膜压力分布图如图5所示。由图可知,在气膜正压处气体流量增加,气膜压力增大;而气膜负压处气体量减少,气膜压力减小。因此气膜压力为正处为转子边界提供了更高的承载力,而气膜压力为负处对转子边界的承载力减小。

图5 轴承二维气膜压力分布图
3.2 下波箔片轴承气膜承载力
由于下波箔片轴承结构的气膜承载力明显大于其他结构,为进一步研究其对气膜承载力的影响,在不改变波数的前提下,研究波宽分别为4°,6°,8°下气膜承载力随波高的变化情况,如图6所示。
由图6可知:

图6 不同波宽的下波箔片轴承承载力对比
1)波高小于0.5 mm时,轴承承载力随波高的增加快速提高;波宽为4°时,波高大于0.7 mm后,轴承承载力随波高的增加缓慢下降;波宽为6°,8°时,波高大于0.5 mm后,轴承承载力随波高的增加出现缓慢下降。这是因为波宽越大,轴承的气膜流场变化区域越大,气膜压力分布变化越明显,而在波高增大到一定程度后,气体运动速度减小,气膜压力反而有减小的趋势。
2)波高小于0.6 mm时,波宽越大,轴承承载力越大;波高大于0.7 mm后,4°波宽的下波箔片轴承承载力略大于6°,这是因为此时4°波宽的下波箔片轴承的箔片结构接近半圆或大于半圆,导致气膜压力分布增大。
当轴承的偏位角θ设置为0时,此时圆轴承左、右半部分分别为气膜正压、负压最大区,而波宽为8°的下波箔片轴承气膜承载力较大,无法确定是左半部分的结构改变对轴承气膜承载力影响更大,因此该结构分别只保留左、右半部分波形(图2c)进行研究,即左、右半部分下波箔片轴承波数为8。
不同波数下轴承的气膜承载力如图7所示。由图可知,左、右半部分波形的下波箔片轴承承载力随波高的变化情况相似,说明左、右分布的波形对轴承承载力影响不大,这是因为其提供的气膜压力大部分用于抵消转子与轴承的摩擦力。

图7 不同波数下波箔片轴承承载力对比
3.3 三维轴承模型的气膜压力
对箔片轴承建立三维模型进行分析可以得到气膜在轴向、径向、周向的流体规律,计算分析得到的承载力变化情况更贴近实际工况。
对于长度为2 mm的短轴承,更加适应当前微型透平机械的发展方向。将箔片轴承进、出口处设置为环境压力,只考虑轴承与转子之间流体气膜的动力特性情况,计算轴承的气膜承载力。
3种轴承的三维承载力对比如图8所示。由图可知,上波箔片轴承的三维气膜承载力优于其他几种类型结构,该结果与箔片轴承二维分析中上波箔片轴承的气膜承载力最高的结果类似。而在三维流场分析中,气膜承载力相比二维流场小很多。这是由于所研究的轴承是短轴承,设置两端进、出口压力相等后,由于气体流速很快,在轴向方向上的气膜压力并不会比环境压力大很多,因此轴承所能提供的承载力也不会很大,符合转子低速旋转时气体轴承承载力低的规律。

图8 不同轴承的三维承载力对比
刚性表面圆轴承与下波箔片轴承三维气膜压力分布的对比如图9所示。由图可知,刚性表面圆轴承的气膜压力最大、最小值在气膜厚度最小处的两边;在改变箔片结构后,下波箔片轴承气膜压力分布更均匀,最大值出现在转子下半部分多个部位,使得气膜对转子边界的压力大部分作用在垂直向上的位置,根据理论分析中气膜承载力的求解公式,压力分布越大,轴颈的承载力越大,由此可知下波箔片轴承气膜承载力大于刚性表面圆轴承的承载力。

图9 轴承三维气膜压力分布图
3.4 小结
综上可得:在一般情况下,下波箔片轴承的气膜流场对转子提供的承载力大于其他类型的箔片轴承。
4 结论
1)以箔片结构中箔片的波高、波宽、波数为变量,控制计算参数相同,下波箔片轴承的气膜承载力明显优于其他轴承。
2)对于下波箔片轴承,在波数一定的情况下,波宽越大,轴承气膜流场特性与承载特性越好。箔片的分布状态对轴承气膜特性的影响较大,箔片布满下半圆的箔片轴承气膜承载特性优于箔片只分布于左、右下半圆的箔片轴承。
3)箔片轴承的二维、三维气膜流场动力特性规律基本相似,相同结构参数下,下波箔片轴承提供的承载力远大于其他类型的箔片轴承。
