矩形静压推力轴承表面平面度与粗糙度的综合分形模拟

张美红，董皓，赵晓龙，刘波，张君安

(西安工业大学 机电工程学院，西安 710021)

1 引言

矩形静压推力轴承是根据气体润滑技术开发的精密机械元件，加工精度较高[1]。为从理论上分析此类轴承的润滑性能，模拟其下表面微观轮廓(图1)是关键性的第1步。

图1 矩形静压推力轴承下表面模型

目前，分形几何作为一种新的数学理论，已被广泛应用于表面微观形貌的研究[2-3]。文献[4]基于分形学中的Weierstrass-Mandelbrot函数建立了粗糙表面的分形模型，即M-B模型；文献[5]提出了用于描述自然界随机分形的分数布朗模型；文献[6-7]则基于分形插值理论提出了分形插值曲面模型，利用曲面上的部分信息和特征拟合出曲面的整体形态。

为模拟矩形静压推力轴承下表面的真实轮廓形貌，结合轴承表面特征，利用分形插值曲面法对其表面平面度和粗糙度进行综合分形模拟，为计算静压止推轴承的润滑性能奠定基础。

2 矩形静压推力轴承表面特征

尽管矩形静压止推轴承的表面加工精度很高，但从微观角度，其表面形貌仍然由许多凸峰和凹谷组成，相邻2个波峰或2个波谷之间的距离很小，肉眼难以区分。其中粗糙度轮廓波峰之间的距离通常小于1 mm，表面波纹度的波距通常为1～10 mm，几何形状轮廓(平面度误差)的波距通常大于10 mm，且三者总是同时存在同一个表面。另外，矩形静压推力轴承表面多采用研磨的加工方式，研磨过程中会不同程度地出现边缘塌边现象[8]，从而使平面度误差变大。因此，需要模拟一个同时具有平面度和粗糙度特征的轴承表面。

表面微观形貌模拟通常有M-B模型、分数布朗模型以及分形插值模型。用10 mm×10 mm作为采样区域，采样间距为0.1 mm时，通过M-B模型、分数布朗模型所形成的表面轮廓如图2所示。从图中可以看出，对于这2种模型，参数一旦确定，表面形貌也唯一确定，且都表征的是表面粗糙度。分形插值模型则是利用曲面上的部分信息拟合出曲面的整体形貌，因此原始曲面形貌的变化会导致分形插值后曲面的几何形状也发生变化，且压缩比的变化也会导致表面粗糙度的变化。基于同一原始曲面，选取不同的压缩比α时得到的具有不同维数的粗糙表面形貌如图3所示。

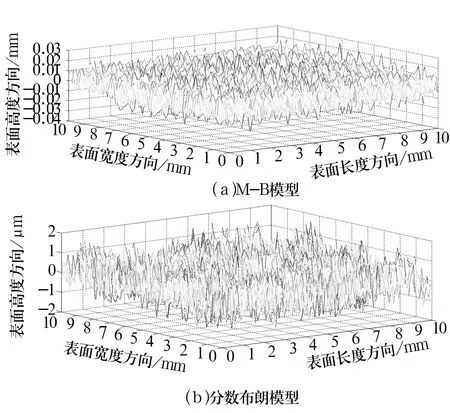
图2 表面轮廓的模拟

因此，结合轴承表面特征及3种模型所模拟表面形貌的相互比较，选定分形插值模型来模拟矩形静压推力轴承下表面的微观形貌。

3 矩形静压推力轴承表面模拟实例

3.1 原始曲面的建立

将轴承下表面平面度测量数据作为插值前的原始数据。传统的平面测量为消除塌边情形对结果的影响，在测量400 mm×400 mm的表面平面度时会在上下左右边缘各留5 mm，共测25个点。为模拟塌边情形，在传统测量数据的基础上另外测量了轴承表面边缘的多组数据，结果见表1。基于表1中数据，需要进行插值的矩形静压推力轴承原始曲面如图4所示，很明显可以看出轴承表面边缘有塌边现象。

图4 矩形静压推力轴承原始曲面

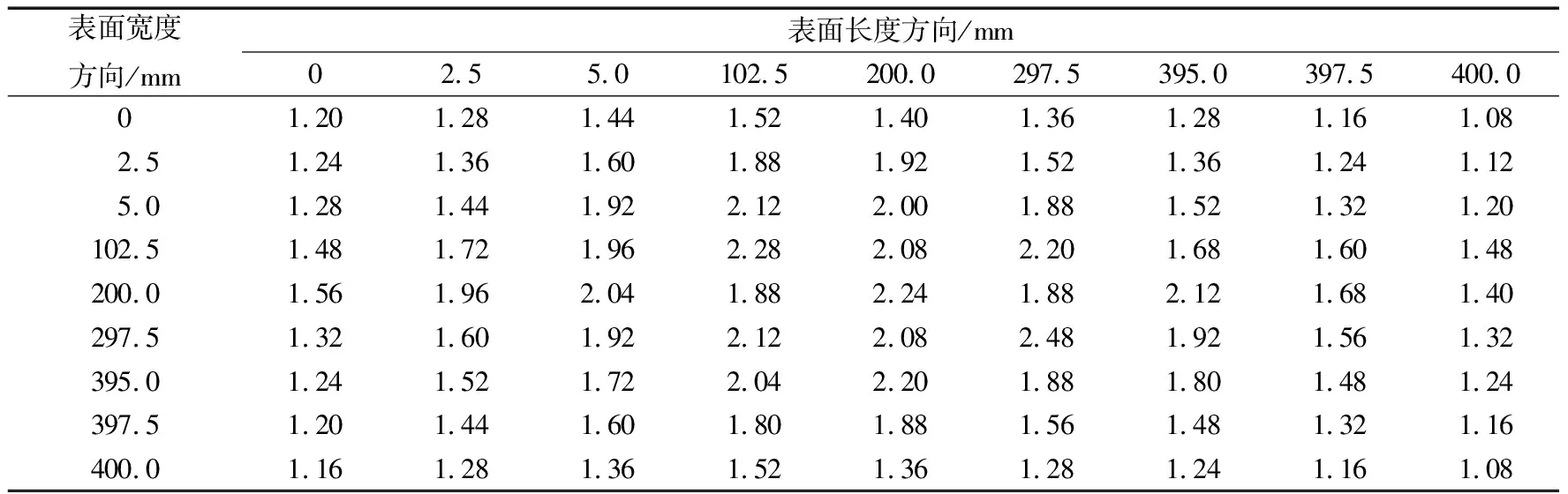
表1 矩形静压推力轴承下表面平面度测量数据

3.2 表面形貌的分区域插值模拟

如果将原始曲面进行整体分形插值，由于分形理论中自相似性特征的存在，分形插值后的表面形貌中间部分也会出现塌边情形，与实际情况不符。因此采用分区域插值，即将原始曲面分为如图5所示的9个区域，分别为中间部分、4个边缘以及4个边角，各区域的原始曲面如图6所示。

图5 矩形静压推力轴承下表面的区域划分

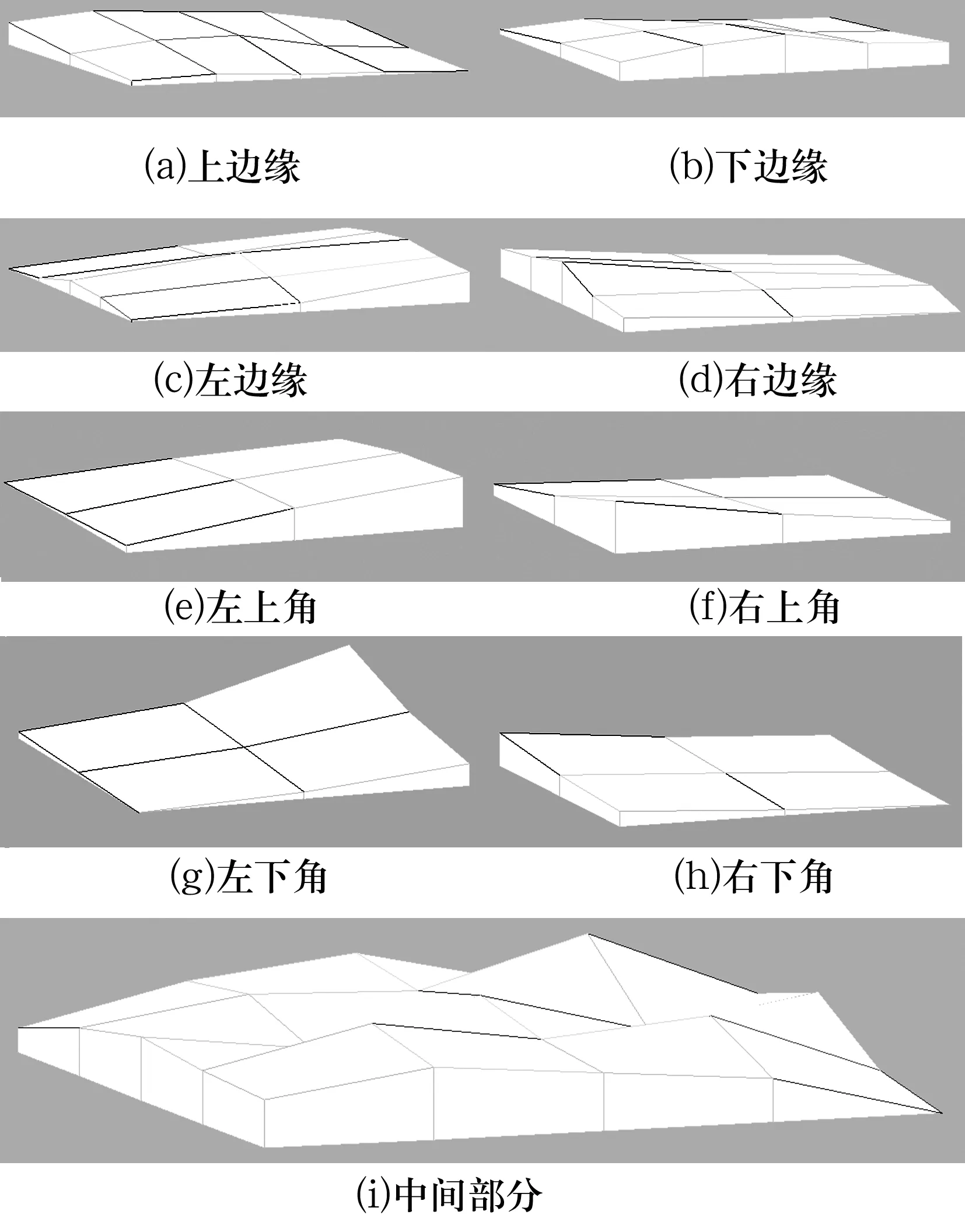
图6 各区域的原始曲面

基于分形插值曲面数学理论，运用MATLAB将9个区域同时进行插值绘制出第1次插值后的曲面如图7所示。

对于同一组插值数据，选取不同的垂直因子α值(压缩比)，就可得到具有不同分形维数的粗糙表面。从图7可以看出：垂直因子越小，平面度特征越明显；垂直因子越大，表面越粗糙，随着垂直因子的增大，粗糙度特征越来越明显。

在第1次插值的基础上，反复迭代从而得到不同程度的静压推力轴承分形插值曲面，垂直比例因子α=0.3时第2次及第3次插值所生成的曲面如图8所示。

从图7b和图8可以看出，当垂直因子一定时，随着插值次数的增大，粗糙度特征越来越明显。且平面度(几何形状)特征和粗糙度特征可以同时显现出来，完成了对静压推力轴承表面粗糙度和平面度的综合模拟。

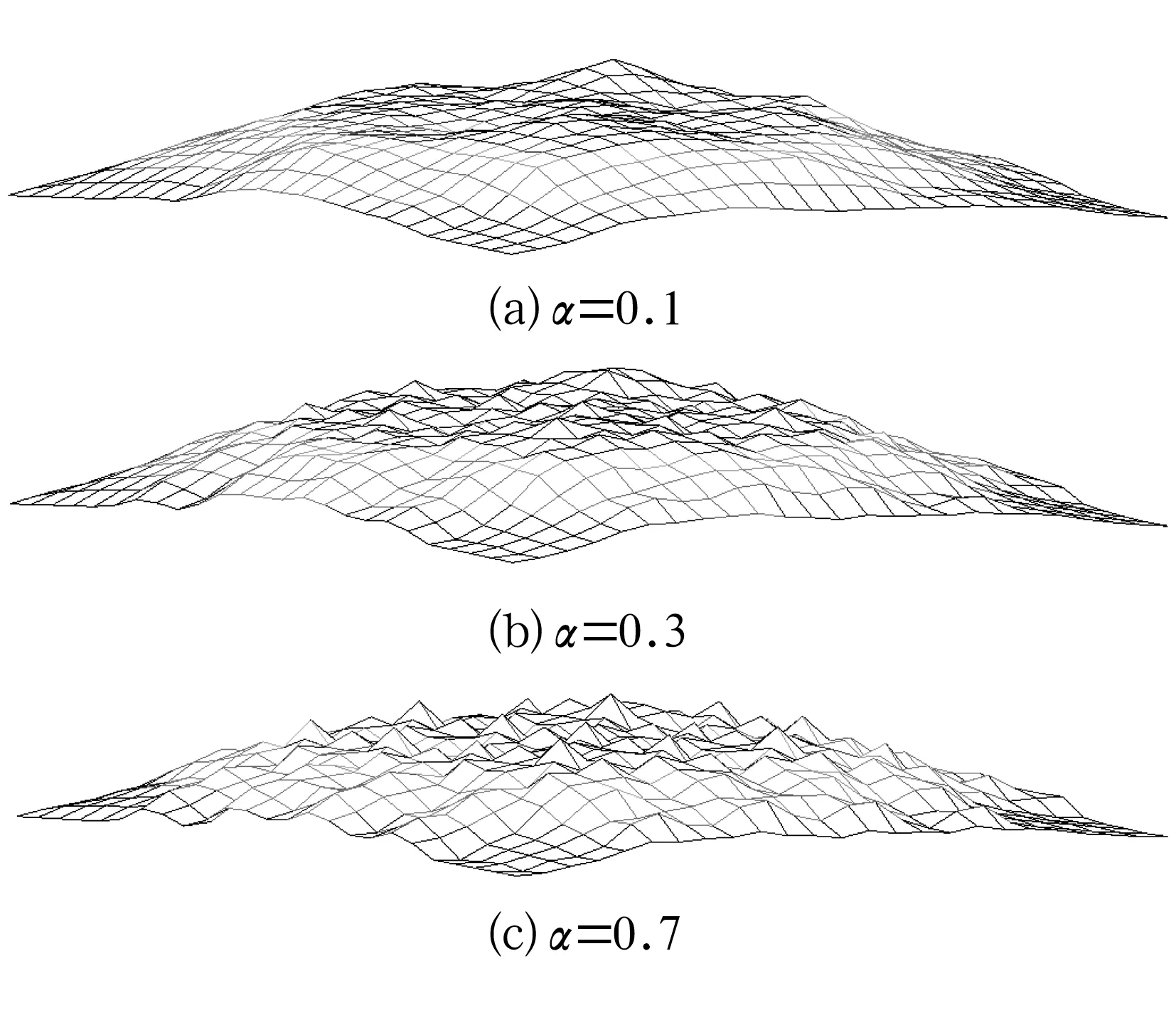
图7 第1次插值后轴承下表面轮廓形貌

图8 轴承下表面分形插值曲面(α=0.3)

为验证该方法对矩形静压推力轴承表面边缘塌边情形的模拟是否符合实际情况，与利用电子水平仪[9]得到的轴承下表面平面度检测结果(图9)进行了对比。从图中可以看出，轴承边缘确实出现塌边情形，说明结合平面度测量数据将原始数据进行分区域插值模拟出的边缘塌边符合真实情况。

图9 轴承下表面平面度仿真图

4 结束语

基于分形几何学，结合矩形静压推力轴承的表面特征，选取分形理论中的分形插值模型对轴承下表面的微观形貌进行了数值模拟，研究发现：

1)利用分形插值模型模拟出的轴承下表面形貌能够同时反映出平面度及粗糙度特征。

2)将原始曲面数据进行分区域插值模拟可以避免轴承表面中间部分出现塌边的情形，模拟结果接近轴承表面真实形貌。