输送带跑偏对驱动滚筒可靠性和优化设计的影响

2018-07-23樊智敏尹兆明马秋艳

橡胶工业 2018年7期

樊智敏，尹兆明，马秋艳

（1.青岛科技大学机电工程学院，山东青岛 266061；2.青岛市技师学院轨道交通学院，山东青岛 266229）

带式输送机作为重要的散装物料输送设备，因结构简单、可靠性强、维护方便、费用低廉而被广泛应用于煤矿、石油、化工等领域。带式输送机工作时，以输送带作为牵引和承载构件，输送带由与驱动滚筒间的摩擦力驱动。驱动滚筒是带式输送机的重要构件，其运行的安全稳定性在整个输送机系统中具有举足轻重的作用[1]。带式输送机由于在制造、安装和使用等方面存在一些问题，使输送带经常出现跑偏现象[2]。输送带作为柔性元件在动力学上表现为显著的粘弹性，在工作过程中存在粘弹性、大位移和大变形的耦合作用，能改变驱动滚筒的受力情况，导致其传动精度下降，并加快其疲劳损坏[3-4]。目前，驱动滚筒设计一般采用许用应力法、经验公式法和类比法，忽略输送带跑偏的影响，并常常通过增大安全倍数提高可靠性，这不仅会增大驱动滚筒的结构尺寸、质量和制造成本，而且使其可靠性与优化设计的计算结果存在较大误差[5]。

本工作以带式输送机驱动滚筒为研究对象，利用SolidWorks软件建立驱动滚筒实体模型，将其导入到Ansys Workbench有限元分析软件中，对比分析输送带在正常运行工况和跑偏工况下驱动滚筒的受力情况及驱动滚筒设计变量对目标函数的灵敏度等，研究输送带跑偏对驱动滚筒可靠性和优化设计的影响，为驱动滚筒优化设计和可靠性提高提供科学依据，避免设计的盲目性。

1 驱动滚筒受力分析

输送带跑偏是带式输送机运行过程中最常见的现象，导致输送带跑偏的原因很多，本研究以驱动滚筒轴线偏移引起的跑偏为例进行分析。驱动滚筒作为带式输送机的主要受力构件，不仅承受自身重力、输送带张力和轴端输入转矩，还承受与输送带简的摩擦力作用。

1.1 输送带跑偏时驱动滚筒的周向受力

在输送带跑偏工况下，驱动滚筒圆周方向上的受力如图1所示。

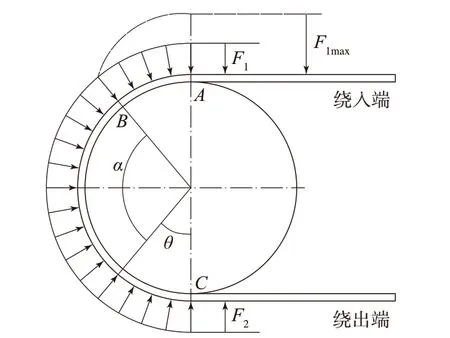
图1 驱动滚筒周向受力分析

本工作主要研究驱动滚筒的应力应变情况，假设驱动滚筒上输送带张力不存在静止弧，滑动弧占满整个围包角[6]。由带式输送机的传动理论和欧拉公式可知，在包角α范围内，输送带上任意一点张力（Fθ）为

式中，F2为输送带绕出端的张力，N；μ为输送带与驱动滚筒之间的摩擦因数；θ为输送带与驱动滚筒分离点至绕出的弧度，rad。

驱动滚筒在θ处单位表面受到输送带对其产生的面压力（Pθ）为

式中，b为输送带宽度，mm；d为驱动滚筒直径，mm。

驱动滚筒在θ处单位表面受到的摩擦力（fθ）为

1.2 输送带跑偏时驱动滚筒的轴向受力

在输送带跑偏工况下，驱动滚筒轴线方向上的受力如图2所示。输送带与驱动滚筒之间的张力（P）可分解为使输送带横向移动的轴向力（P1）和使输送带纵向运行的驱动力（P2）。

图2 驱动滚筒轴向受力分析

式中，φ为驱动滚筒轴线偏移角。

由式（4）知，轴向力的大小由输送带与驱动滚筒之间的张力和驱动滚筒轴线偏移角度决定。当轴向力不小于输送带与驱动滚筒之间的极限摩擦力时，输送带会出现跑偏现象；当轴向力小于该极限摩擦力时，输送带虽不会出现跑偏现象，但在驱动滚筒上一直存在轴向力的作用。

2 输送带跑偏对驱动滚筒可靠性的影响

2.1 驱动滚筒的几何参数和材料参数

以某型号等截面双端驱动滚筒为例进行分析。主要构件的尺寸参数（mm）为：筒体长度1 600，带宽 1 400，辐板间距 1 200，筒壳外直径 1 670，筒壳厚度 38，辐板内直径 695，辐板厚度 60，轮辐内直径 495，轮辐宽度 170，轴总长度 2 566，轴承宽度 500，轴端外直径200。载荷参数为：合力 1 200 kN，扭矩 280 kN·m，带速 0.3 m·s-1，摩擦因数 0.3，包角

180°，跑偏时轴向力 300 kN，正常运行时轴向力为零。筒壳、滚筒轴、轮辐和轮毂的钢材牌号分别为Q235，45#，ZG25和ZG25；滚筒轴的弹性模量为1.93×105MPa，其他3个部件均为2.0×105MPa；筒壳和滚筒轴的泊松比为0.28，轮辐和轮毂为0.30；密度均为7.85 Mg·m-3。

2.2 驱动滚筒模型的建立

输送带跑偏时，驱动滚筒受力情况比较复杂，为提高计算效率，需在有限元分析之前对带式输送机虚拟样机进行简化处理：（1）将构件的倒角、圆角、孔、槽、凸台等特征进行压缩；（2）假设整个驱动滚筒的焊缝工艺合格；（3）简化轴承，用等效约束代替；（4）将一些不影响整体结构性能的小零件如密封圈、螺母、起吊螺栓等压缩掉；（5）输送带在驱动滚筒筒壳的整个围包弧上无滑动现象，圆周力的传递符合欧拉公式[7-9]。

根据驱动滚筒主要零部件参数，结合简化处理结果，运用SolidWorks三维软件对驱动滚筒进行建模。将创建好的模型导入到Ansys Workbench有限元分析软件中，根据驱动滚筒的材料属性定义，对驱动滚筒模型进行网格划分，如图3所示。

图3 驱动滚筒的网格模型

2.3 两种工况下驱动滚筒应力应变对比分析

根据驱动滚筒在正常运行和跑偏两种工况下的受力情况施加约束和载荷，并对其应力应变情况进行对比分析。

2.3.1 位移变形分析

驱动滚筒位移变形对比如图4所示。

图4 驱动滚筒位移变形对比

由图4可知，带式输送机驱动滚筒在两种工况下运行时，驱动滚筒的最大变形均出现在输送带与筒壳接触的中心部位。输送带在正常工况下运行时，驱动滚筒筒壳的最大变形量为0.149 mm，两侧的变形量呈对称分布。输送带在跑偏工况下运行时，驱动滚筒筒壳的受力情况发生变化，整体变形量相对较大，筒壳的最大变形量为0.233 mm，且输送带跑偏一侧的变形量相对较大，呈不均匀分布。对比两种工况下驱动滚筒的位移变形情况可知，输送带跑偏不仅会使驱动滚筒筒壳的最大变形量增大，还能使其分布范围扩大，且输送带跑偏一侧筒壳的变形量相对较大。

2.3.2 等效应力分析

驱动滚筒等效应力分布对比如图5所示。

由图5（a）可知，输送带在正常工况下运行时，驱动滚筒筒壳的最大应力出现在两侧辐板与筒壳的接触处，其值为18.915 MPa，且两侧应力大小呈对称分布。由图5（b）可知，输送带在跑偏工况下运行时，在输送带跑偏一侧筒壳与辐板接触处和轮毂与辐板接触处的应力相对较大，其最大值为28.845 MPa。对比可知，输送带跑偏时，在驱动滚筒上产生的最大应力值较大，且输送带跑偏一侧的整体应力值明显高于另一侧，说明输送带跑偏不仅能使驱动滚筒的最大应力增大，而且还能使其出现的位置发生改变。

图5 驱动滚筒等效应力分布对比

2.4 轴向力对驱动滚筒应力应变分布的影响

由式（4）可知，驱动滚筒的偏移角度不同，与输送带间产生的轴向力值也不相同。通过分析得到轴向力变化对驱动滚筒最大应力和最大变形量的影响，如表1所示。

由表1可知，随着轴向力的增大，驱动滚筒最大应力和最大变形量的值也逐渐增大。轴向力小于100 kN时，驱动滚筒最大变形量的变化幅度较小；轴向力大于100 kN时，其变化幅度增大，且随着轴向力的增大，驱动滚筒上最大变形量的分布范围也逐渐扩大。轴向力小于450 kN时，驱动滚筒最大应力的变化幅度较小；轴向力大于450 kN时，其变化幅度相对较大，且随着轴向力的增大，驱动滚筒上出现最大应力的位置也逐渐发生变化。轴向力较小时，驱动滚筒的最大应力出现在两侧辐板与筒壳的接触处；随着轴向力的增大，驱动滚筒上出现最大应力的位置转移到输送带跑偏一侧辐板与筒壳的接触处；当轴向力增大到一定值后，驱动滚筒的最大应力同时出现在输送带跑偏一侧辐板与筒壳和轮毂的接触处。

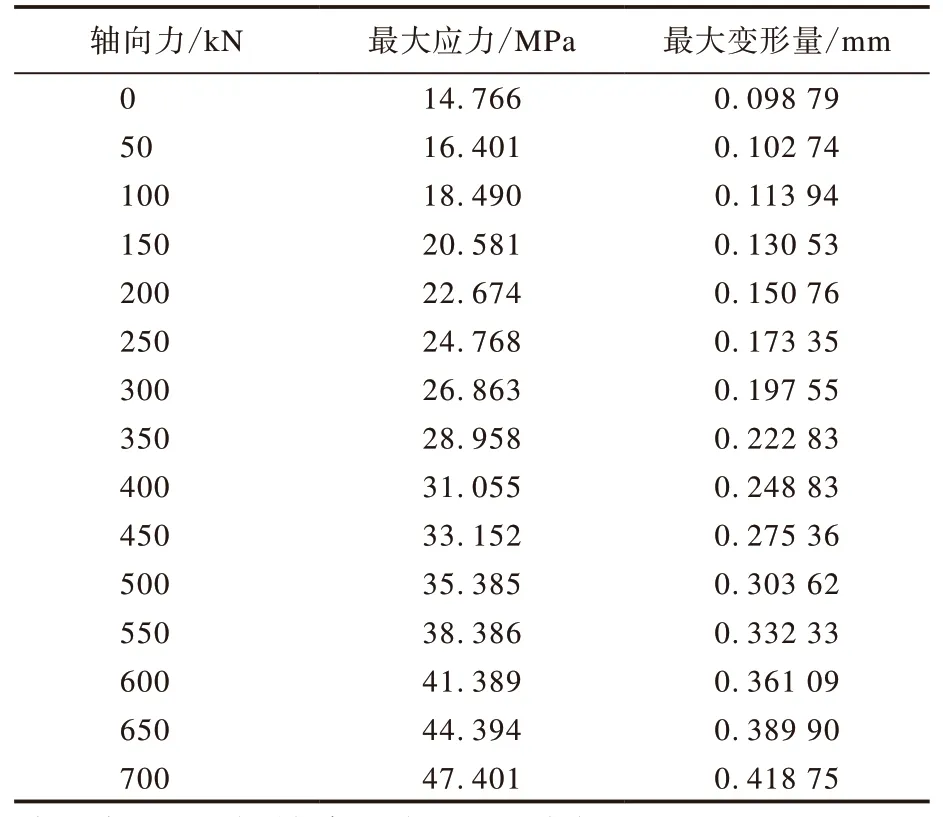
表1 轴向力对驱动滚筒最大应力和最大变形量的影响

3 输送带跑偏对驱动滚筒优化设计的影响

在正常运行工况下，由于输送带的物理特性，其与驱动滚筒间始终存在较小的轴向力，使其产生小幅偏移，影响相关零部件的使用寿命。因此，在对驱动滚筒进行优化设计时需要考虑输送带跑偏的影响。

3.1 两种工况下的灵敏度对比

通过对驱动滚筒应力应变的有限元分析可知，输送带跑偏会对驱动滚筒筒壳、轮毂和辐板的应力应变产生较大的影响，因此选取驱动滚筒辐板厚度、辐板间距、筒壳厚度和轮毂宽度为设计变量，以驱动滚筒的最大变形量、最大应力和质量为目标函数。辐板厚度、辐板间距、筒壳厚度和轮毂宽度的初始值（上限/下限，mm）分别为60（70/50），1 200（1 500/900），38（44/32）和170（190/150）。

在灵敏度分析中，设计变量对目标函数灵敏度的绝对值越大，对目标函数的影响越大。灵敏度为正值，表示参数增大时目标函数值相应增大；灵敏度为负值，表示当参数减小时目标函数值相应减小[10]。通过分析得到两种工况下驱动滚筒所选设计变量对目标函数的灵敏度，如表2所示。

表2 设计变量对目标函数的灵敏度

对比可知，在输送带跑偏工况下，各设计变量对驱动滚筒最大应力和最大变形量的灵敏度影响明显增强，对质量的灵敏度无变化，说明输送带跑偏影响所选设计变量对驱动滚筒最大应力和最大变形量的灵敏度，而对质量的灵敏度无影响。此外，在两种工况下，辐板厚度和筒壳厚度对驱动滚筒目标函数灵敏度的影响相对较大，因此在对驱动滚筒进行优化设计时，可选取辐板厚度和筒壳厚度为主要设计变量。

3.2 设计变量参数变化对目标函数的影响

由两种工况下驱动滚筒设计变量对目标函数灵敏度的对比分析可知，无论输送带跑偏与否，驱动滚筒设计变量对质量的灵敏度是相同的。因此，仅考虑主要设计变量（筒壳厚度和辐板厚度）对驱动滚筒最大应力和最大变形量的影响。

（1）单个设计变量对驱动滚筒目标函数的影响分别如表3和4所示。

由表3和4可以看出，驱动滚筒的最大变形量和最大应力在两种工况下随筒壳厚度和辐板厚度增大的变化趋势相似。在一定范围内，随筒壳厚度和辐板厚度的增大，驱动滚筒的最大变形量均逐渐减小，且在输送带跑偏工况下的变化幅度较大，而驱动滚筒的最大应力均先增大后减小，但两种工况下的变化幅度相差不大。由此可见，输送带跑偏使驱动滚筒的最大变形量和最大应力增大，且在输送带跑偏工况下，随筒壳厚度和辐板厚度的增大，最大变形量的变化幅度较大，最大应力的变化幅度与正常运行工况相差不大。

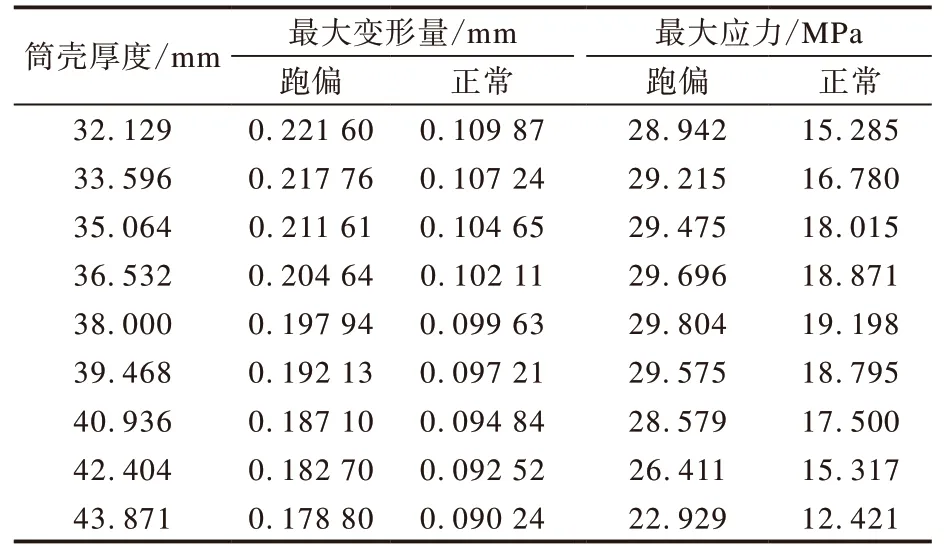
表3 筒壳厚度对驱动滚筒应力应变的影响

表4 辐板厚度对驱动滚筒应力应变的影响

（2）两个设计变量同时变化对驱动滚筒目标函数的影响如图6和7所示。

图6 输送带正常运行工况下筒壳厚度和辐板厚度对驱动滚筒应力应变的影响

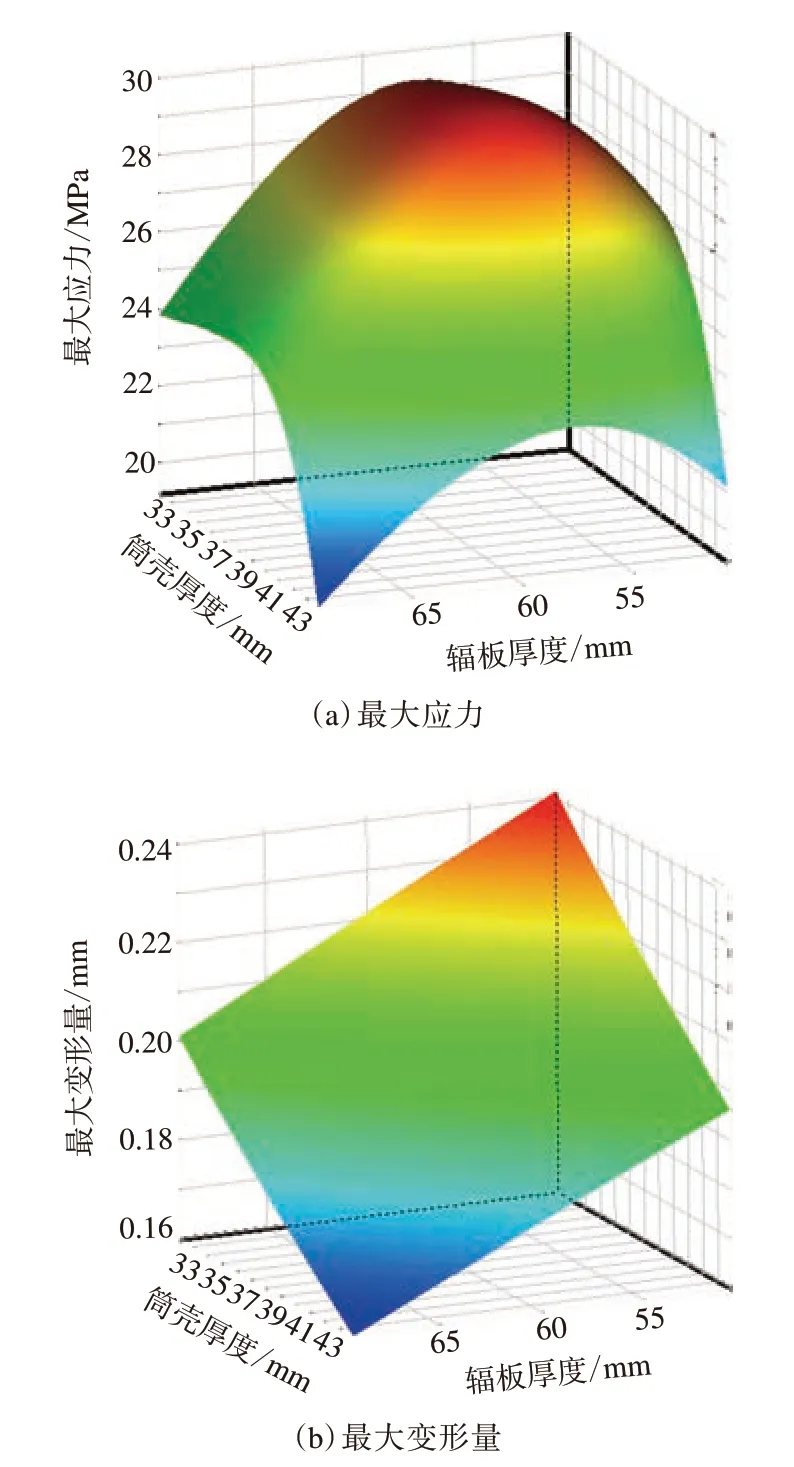
图7 输送带跑偏工况下筒壳厚度和辐板厚度对驱动滚筒应力应变的影响

由图6和7对比可知，在两种不同工况下，同时改变辐板厚度和筒壳厚度会对驱动滚筒最大应力和最大变形量产生不同影响。相对正常运行工况，在输送带跑偏工况下，两设计参数同时改变，驱动滚筒的最大应力和最大变形量均增大，其分布范围也发生改变，最大应力的分布范围扩大，最大变形量的分布范围缩小。此外，仅改变某一设计变量，易使驱动滚筒产生应力集中，加速驱动滚筒的损坏。可见，输送带跑偏会改变设计变量对驱动滚筒应力应变的影响。因此，对驱动滚筒进行优化设计时，不仅应考虑多个设计变量的综合影响，还应考虑运行过程中输送带跑偏的影响。