巧妙转化 灵活变通——从“化归法”专题习题课说起

☉江苏省常熟市尚湖高级中学 孙 丹

“化归”即转化，是在分析、解决数学问题的时候采用某种数学方法对问题进行变换，使之转化进而达到解决的一种方法.实际上，化归思想已经渗透到了高中数学内容的方方面面，数学离不开化归思想，比如将未知量向已知量转化，现实问题向数学模型转化，复杂问题向简单问题转化等.可以说，化归思想是解决数学问题的有效方法，也是一种应用极广的数学思维方式.

最近，笔者听了一高三习题课，主题就是“化归与转化”.授课老师结合一系列的练习题向学生讲解了这一思想方法的常用情形，引导学生认识与掌握这一思想方法.个人认为教学效果显著，现从以下几点进行论述.

适用情形一：追本溯源，复杂函数简化处理

【教师】同学们，高中阶段我们学习的函数很多，有反比例函数、一次函数、二次函数、指数函数、对数函数等，这些基本的函数类型就是大家处理复杂函数的题根，题根能给我们的解答过程提供化归的方向.因此，同学们在遇到一些复合函数时可以尝试将其向题根转化，变成初等函数，问题也就迎刃而解了.下面我们以具体的练习进行说明.

【案例展示】已知f（x）=cos2x-sinx，求函数f（x）的值域.

【教师提问】同学们，拿到这道题，大家有什么思路？

【学生甲】f（x）涉及到了正弦函数与余弦函数，首先需要统一，可以把cos2x转化为1-2sin2x，函数f（x）也就变成了-2sin2x-sinx+1.

【教师提问】没错，这是比较合理的处理方法，之后要怎么求解函数f（x）的值域呢？直接用三角函数的内容？

【学生乙】可以换元处理，令a=sinx，原函数也就变成了f（a）=-2a2-a+1，根据三角函数的值域可以知道a的取值范围为［-1，1］.二次函数值域的求解就很容易了，结合图像（如图1）我们就知道值域为

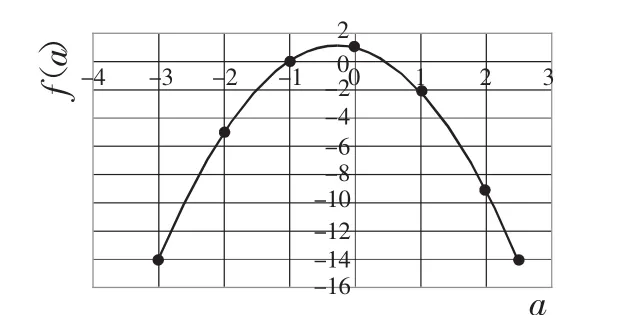
图1

【评析】二次型函数、高次函数等都是常考题型，这些函数看起来形式复杂，难度很大，其实归根结底就是对二次函数的考察，只要进行一定的转化处理，进行变量代换，明确新的变量的取值范围，结合二次函数的相关性质，问题很容易解决.

适用情形二：不等式转化为函数

不等式是高中数学的重要内容，也是高考的必考内容.对于不等式的考查往往不会局限在这个单一的知识点上，而是与其他内容相结合，形成更为复杂的综合题，这些综合题对学生的解题方法、思维、能力的要求更高.解题时，学生需要将题目还原成一个个知识点，逐步解决，这个过程也是“化归思想”的体现.下面以不等式转化为函数为例进行说明.

【案例展示】已知x的取值范围为［-1，2］时，不等式a≥x2-2x-1恒成立，求实数a的取值范围.

【教师提问】在x的取值范围内，a≥x2-2x-1恒成立，这个条件说明了什么？

【学生甲】无论x取什么值，a都要比x2-2x-1取到的值大.

【教师提问】怎么把这个条件转化成数学语言呢？

【学生乙】在x∈［-1，2］的范围内，a大于等于x2-2x-1的最大值.

【教师提问】没错，这么一来，这道不等式问题就转化成了函数问题.哪位同学在黑板上解答一下.

【学生丙板书】设f（x）=x2-2x-1=（x-1）2-2，

因为x的取值范围为［-1，2］，

所以在x=-1时，f（x）max=2，

所以a∈［2，+∞）.

【评析】不等式反映的是不同变量之间的相互制约关系，是一种变量之间的内在联系.不等式与函数的单调性、有界性等性质之间具有较强的联系，因此在处理不等式时将其转化为函数问题是一种合理并且有效的解决方法.

适用情形三：立体几何代数化

【案例展示】已知：在三棱柱ABCA1B1C1中，AA1C1C是一个正方形，边长为4，与面ABC相垂直.AB=3，BC=5.

求解：二面角A1-BC1-B1的余弦值是多少？

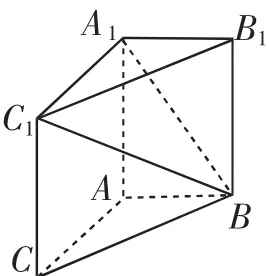
图2

【教师提问】在解决这个问题前，同学们先思考一下，怎样求解二面角？

【学生甲】作两个面交线的垂线，构造三角形.

【教师提问】那这道题用常规方法可以做吗？

【学生甲】有点麻烦，做出来我也不知道对不对.

【教师提问】考试时，答题之前同学们要认真审题，看清每个已知条件，看已知条件满不满足你们选用的方法.这道题如果选用常规方法，计算量显然太大，解答过程也不严谨，很容易会扣过程分.我给同学们提供一个思路，在平面几何中，遇到计算题我们会建立平面坐标系，借助向量进行运算，那么这里应该怎么处理？

【学生乙】建立空间坐标系，用空间向量算.

【教师提问】那乙同学你上来解答一下.

【学生乙板书】由AC2+AB2=BC2，

得AB⊥AC.

又面AA1C1C⊥面ABC，

A1A⊥AC，

所以A1A⊥AB.

所以A1（0，0，4），B（0，3，0），

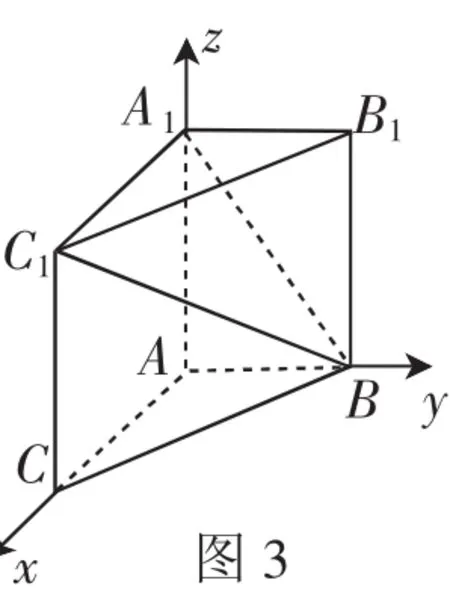
图3

设平面A1BC1的法向量为m=（x1，y1，z1），平面B1BC1的法向量为n=（x2，y2，z2）

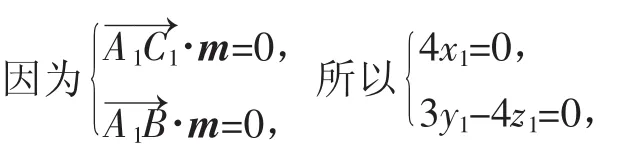
令m=（0，4，3）.

【评析】在解决几何中的计算时，借助向量运算的手段能使得解题过程更为清晰准确.可以说，向量是用代数方法解决几何问题最有效的方法.在立体几何中也是这样，只要建立起适当的空间坐标系，那么立体几何中的所有运算都可以转化为代数问题进行解决.

适用情形四：定点定值转化为恒等式

在高中数学内容体系中，解析几何是教学的重点，也是难点.以圆锥曲线为例，对于这一部分的知识内容，相当一部分学生不能理解圆锥曲线相关内容所蕴含的数学思想以及数学方法，拿到题目就是套公式进行计算，而不是仔细审题，联系其他知识点进行转化.许多同学在解决圆锥曲线计算题时都会遇到计算量巨大的问题，有同学表示算到最后不知道自己算的是什么，式子越算越复杂，就是求不出结果.下面以具体教学案例为说明.

【教师提问】同学们，在解决解析几何问题时，大家要养成将已知条件量化的习惯，寻找题目表达出来的各种数量关系.哪位同学来说一下题目中能提炼出哪些数量关系？

【学生】根据题干信息可以知道A点的坐标为（-a，0），F的坐标为（-c，0）.P为圆O上的动点，设其为（x，y）.假设=u，所以有关系式：

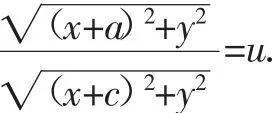
因为P在圆O：x2+y2=b2上，

所以满足a2+b2-u2（b2+c2）+（2a-2u2c）x=0，

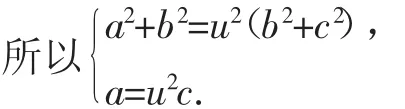
【教师提问】你继续算下去，看能不能得到最终结果.

【评析】在高考中，有关圆锥曲线计算结果恒为定值或者图形恒过定点是常考题型，这类题目如果用常规方法进行计算是很复杂的，显然命题人考核的重点并不是计算，而是数学思想的应用.因此，同学们要熟练掌握化归的思想方法，善于把这类问题转化为关于某个变量的恒等式问题，进而简化代数运算.

这节习题课后，笔者认识到“化归”这一思想方法能有效实现由实际问题向数学问题、复杂问题向简单问题、陌生问题向熟悉问题等的转化.当然，要做到这种变通，就需要学生具备较强的解题能力，而解题能力的关键就是基础理论知识.因此在日常的教学过程中，教师要强化基础训练，引导学生掌握好常规的思维方法.在这个基础上引导学生进行化归思维方法训练，做到举一反三，触类旁通，提升数学解题能力.J