一道平几题的多解剖析

☉江苏省高邮市第一中学 沈红梅

【例题】（石家庄市2018届高中毕业班教学质量检测（一）·16）如图1所示，平面四边形ABCD的对角线交点位于四边形的内部，AB=1，BC=2 ，AC=CD，AC⊥CD，当∠ABC变化时，对角线BD的最大值为______.

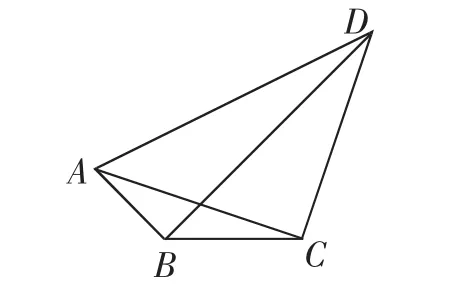
图1

解题思路：（1）建立不同三角形内的边角关系，得到相应的解析式来求解最值；（2）将整个平面图形放在平面直角坐标系中，通过坐标建立关系式；（3）将所要求解的边长转化为边AC的函数关系，结合函数思想来确定相应的最值问题；（4）通过垂直作辅助线，利用三角形相似建立关系式来处理；（5）以静制动，将不在一起的条件创新性地放在一起来处理；（6）将四边形的对角线与四条边通过托勒密不等式建立关系来处理.下面我们具体讨论这六种解法.

思路方向1：解三角形思维是此类问题中最常见的解题方法，也是考虑问题中最易想到的基本方法.设出相应的角，通过三角形的转化，利用不同三角形间的边角关系，再利用正弦定理和余弦定理来转化与处理，结合三角恒等变换，通过三角函数的图像与性质来确定相应的最值问题.本解法的关键是转化与化归，运算时要有耐心，认真细致.

解法1（解三角形法）：设∠ABC=α，∠ACB=β，

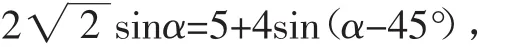
则当α=135°时，BD2有最大值9，BD取得最大值为3.故填3.

思路方向2：涉及平面几何比较难处理时，经常可以考查建系，通过平面直角坐标系的建立，结合解析几何来转化，也是解决此类问题中比较常见的方法之一.巧妙建立平面直角坐标系，把点A放在单位圆上，引入三角参数，结合平面向量的坐标运算以及模的运算，结合三角恒等变换，通过三角函数的图像与性质来确定相应的最值问题.本解法巧在建系，以运算代说明.

解法2（建系法）：以B为坐标原点，BC所在直线为x轴建立平面直角坐标系xBy，则C（，0），设∠ABC=α，则A（cosα，sinα），

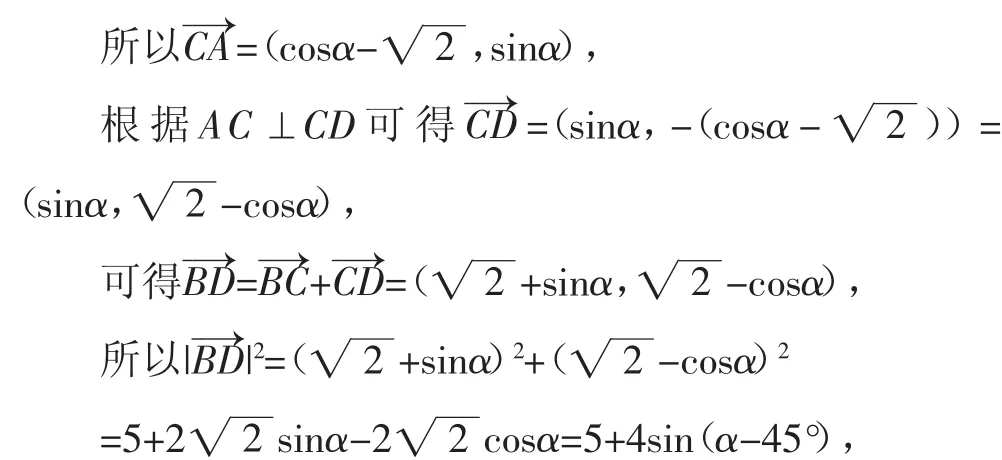
思路方向3：涉及平面几何比较难处理时，经常可以转化为函数，利用函数与方程的关系来处理，这也是解决此类问题中比较常见的方法之一.设AC=CD=x，结合余弦定理求解cos∠ACB的值，通过同角三角函数基本关系式可得sin∠ACB的值，把BD2表示成参数x的关系式，结合函数与方程的思维，利用判别式确定对应的取值范围，进而确定BD的取值范围即可.本解法在得到BD2=2+后，由于判断函数的最值问题的处理方法多样，所以可以利用函数与方程法处理，也可以结合导数法来处理，还可以通过三角换元思维来处理等.

综上所述:中西医结合对甲状腺功能亢进症患者进行治疗能够明显改善甲状腺功能,且临床疗效良好,安全性高,不良反应发生率低,值得广泛推广。

在△ABC中，由余弦定理可得AB2=AC2+BC2-2AC·

则当α=135°时，|B—→D|2有最大值9，BD取得最大值为3.故填3.BC·cos∠ACB，即1=x2+2-2xcos∠ACB，解得cos∠ACB=，结合同角三角函数基本关系式可得sin∠ACB=

在△BCD中，由余弦定理可得

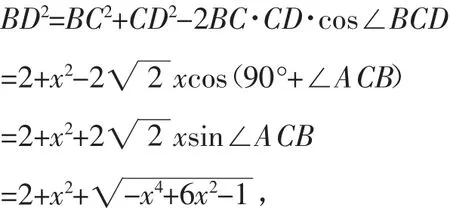
思路方向4：通过过点A、D作BC边上的垂线，把斜三角形问题转化为直角三角形问题，利用直角三角形中的边角关系以及勾股定理来转化，结合三角恒等变换，通过三角函数的图像与性质来确定相应的最值问题.辅助线法在实战中应用广泛，往往可以起到出其不意的效果.

解法4（辅助线法）：设∠ABC=α，如图2，作AE⊥BC，DF⊥BC，

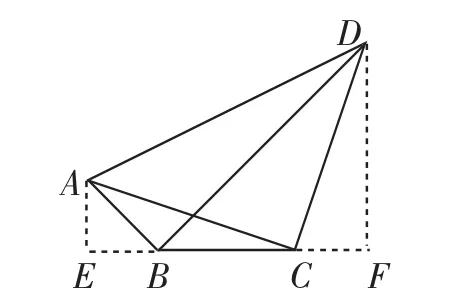
图2

由AC=CD，AC⊥CD，可得Rt△ACE≌Rt△CDF，

所以DF=CE=EB+BC

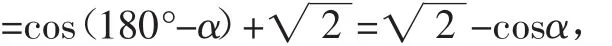
CF=AE=sin（180°-α）=sinα，

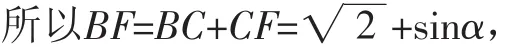
则BD2=BF2+DF2

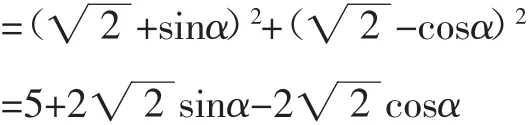
=5+4sin（α-45°），

因此当α=135°时，BD2有最大值9，BD取得最大值为3，故填3.

思路方向5：通过将△ABC绕点C顺时针旋转90°，先结合旋转后对应的边角关系，再利用平面几何的相关知识求解对应的边长问题，最后结合图形，以动制静来处理相应的最值问题.本解法思维巧妙，借助初中平面几何的相关知识来解决高中问题，回归本源.有时采用初中平面几何的知识来解决一些高中的相应数学问题，可以使得问题解决起来更流畅、快捷.

解法5（平几法）：如图3，将△ABC绕点C顺时针旋转90°，

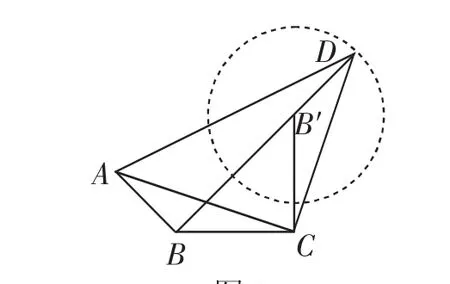
图3

因为AC=CD，AC⊥CD，则旋转过后点A与点D重合，记点B旋转至点B′，

则B′D=1，即点D在以点B′为圆心，半径为1的圆周上，

结合图形可得BD≤BB′+B′D=2+1=3，当且仅当B，B′，D三点共线且点B′在线段BD上时等号成立，故填3.

思路方向6：（托勒密不等式法）本解法涉及凸四边形的对边、对角线等的关系问题，考虑利用特殊的几何定理：托勒密不等式（凸四边形的两组对边乘积和不小于其对角线的乘积，当且仅当四点共圆或共线时等号成立）来处理.处理巧妙，过程简单快捷.本解法涉及的托勒密不等式不属于课本知识，所以学生不易掌握，只是作为一个课外的拓展解法来处理.

解法6：设AC=CD=a，

由托勒密不等式（凸四边形的两组对边乘积和不小于其对角线的乘积，当且仅当四点共圆或共线时等号成立）可得AD·BC+AB·CD≥AC·BD，

通过从多个不同角度来处理，巧妙地把该题的底蕴充分挖掘出来，多角度出发，多方面求解，真正实现对数学知识的融会贯通，充分展现知识的交汇与综合，达到提升能力、拓展应用的目的，进而真正达到在学中“悟”，在“悟”中不断提升解题技能的目的.正如我国著名数学家苏步青先生说过：“学习数学要多做习题，边做边思索，先知其然，然后知其所以然.”J