少一些直接切入，多一些启发和引导——高中数学课堂三种常见现象的分析和对策

☉浙江省温岭市新河中学 郭小剑

高效教学并不等于教师的全盘包办，在教学中，很多教师的操作太过直接，自顾自地跑在问题探索的最前沿，这显然无助于学生的发展和提升，以下是我们教学中亟待改变的常见现象.

一、直接点出学生的错误

数学教育家波利亚有关教学行为总结出“教师十诫”，其中的最后一条是“提供建议，而不是强迫接受”，他在进一步的说明中强调，教师针对学生的错误思路或答案不能直接说“这是错的”，如果教师经常这样操作，将导致学生会在心理上对老师和数学产生一种憎恶.

例1已知f（x）=asin2x+cos2x（a∈R）的函数图像有

学生将函数化归为正弦函数，并表示出对称轴的一般表达式，再结合已知条件确定a的取值，这一解题思路是正确的，但是学生的解答也存在着一些问题，即忽视了a的取，则α应该是一、三象限角，因此对应的正余弦取值应该是同号的，即

在日常教学中，如果遇到这样的情况，很多教师往往一针见血地点出学生的错误，这固然是一种效率极高的操作，但是却在一定程度上挫伤了学生数学学习的兴趣，也让学生失去一次自主发现错误、自行探索真理的机会，这当然无助于学生学习效率的提升.

一般来讲，如果教师不进行提示，学生不会对a的取值情况展开检验，但是如果直截了当地提示学生进行检验，这又是对学生自主思考权力的一种剥夺.

应对策略：面对上述尴尬局面，笔者认为我们可以指导学生探寻不同解法，由此让学生对比出最终答案的差别，自然也就会自发地探求出问题的所在.

二、直接将巧妙方法提供给学生

波利亚的教育理论指出，教师要尽可能地为学生提供发挥主动意识的机会，强调教师不能一下子将所有的秘密全部揭示出来，要尽量让学生自己在探索中发现问题解决的方案.事实上，我们的教学中，很多老师无法做到上述要求.

现象呈现：学生处理时往往会采用这样的思路：

上述方法运算量非常大，而且存在一定的技巧性，很多学生开始的思路正确，但是在运算时陷入僵局.特别是步骤（*），很少有学生能够将分母展开并通过配方让k更加集中.事实上，本题更加巧妙的处理是采用极坐标，即将上述方法中的斜率k变成角.实际教学中，很多教师是直接将方法提供给学生，但是这样的操作必然会剥夺学生学习数学的乐趣.

应对策略：本题的处理关键是对学生进行启发：为什么不能根据步骤（*）的表达式完成求解呢？由于A与B之间特殊的关系，如何对动点A进行刻画可以避开k取零的情形？实践中，我们发现学生在启发下成功地调整思路，用极坐标来表示动点A（ρ1cosθ，ρ1sinθ），B（-ρ2sinθ，ρ2cosθ）.这样即可得到：

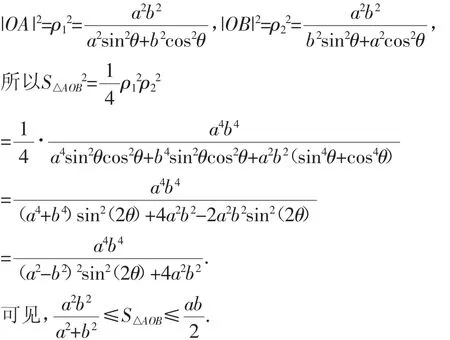
如果教师只是片面地追求讲题效率，直接将作答的方法灌输给学生，而没有给予学生足够的时间进行自主思考和探索，没有对学生予以耐心的启发，学生也只能是暂时性接受到一个问题的答案，至于方法、思想等内容很难浸润学生的内心，所以教师要善于通过启发性的问题引导学生展开探索，由此引导学生实现问题的解决.

三、直接替代学生完成数学问题表征

问题表征是在理解问题的基础上，发现问题结构，并在头脑中构思问题空间的过程，这对问题解决相当重要.在高中数学课堂上，一旦遇到难度较大的问题，很多教师会逐字逐句地阅读问题，并通过列表作图的方式来帮助学生进行问题表征，甚至将解题方法的框架全部为学生搭建好.

例3 已知某数列{an}的每一项都是正整数，对于n=1，2，3，…，有

如果存在m∈N*，当n＞m，且an为奇数时，an恒等于常数p，请确定p的值.

现象呈现：学生在处理上述问题时难度很大，其主要原因是在问题表征上遇到障碍.就数列问题来讲，通常应该将初始项作为已知条件提供出来，但是本题却没有，因此这里的数列可以视为一“抽象数列”.本题的情境指出：若an是奇数，则an+1=3an+5，此时这必然是一个偶数；当an是偶数时，可以将因数中的2提出来，则存在一个最大正整数k，使得an=2kb，此时b是奇数，而an+1=b，由此可知问题所给的数列实际上有着奇偶相间的特点，我们再将条件“如果存在m∈N*，当n＞m，且an为奇数时，an恒等于常数p”这一条件表征为“设an为奇数，则an+1=3an+5为偶为奇数且与an相等”，这样即可很容易地完成对an的确定，即对p值的确定.

以上表征过程难度较大，很多教师直接替代学生完成这一过程，长此以往，学生将形成依赖心理，当再次遇到此类难题，还是很难完成表征.

应对策略：教师在教学中不宜替代学生完成问题的解读过程，而应该通过一些启发性的问题来诱导学生，比如提出以下问题：（1）假设an为一个特殊的偶数，则k如何取值，可以让an+1为奇数？（2）请思考这个数列的各项有何特点？

面对问题，学生要积极发掘和分析题目中的信息，有时单一化的角度很难完成对问题的正确表征，我们要培养学生从多个角度来实现问题表征，以此来提升学生的问题分析能力.