一道函数试题的多解剖析

☉江苏省宜兴第一中学 邵丽霞

例 （2018届江苏省南通、扬州、泰州、淮安、徐州、宿迁二模·14）已知a为常数，函数，则a的所有值为______.

分析：本题的问题背景是给出函数f（x）的最小值，进而确定相应参数的所有取值，当中隐含着函数的基本性质（奇偶性、最值等），而如何根据条件切入、采用哪种方法与知识点来确定函数的最值点是解决问题的关键，也是不同种解法的主要依据.

思路分析1：由题意可得函数（fx）为奇函数，通过对函数（fx）求导，结合导函数为零得到，根据题目条件确定a＞0，进而由f（′x）＞0可得（a-1）［a-（a+1）x2］＞0，通过对参数a分0＜a＜1与a＞1进行分类讨论，根据函数对应定义域下的单调性与单调区来确定最值，进而求解参数的取值.

解法1（导数法1）：由题意知，函数（fx）为奇函数，对其求导得

那么由f′（x）＞0可得（a-1）［a-（a+1）x2］＞0.

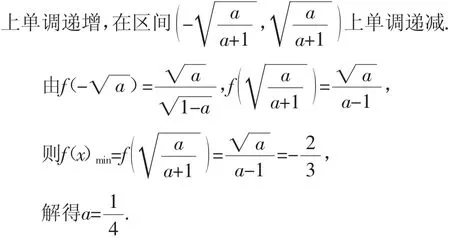
（2）当a＞1时，函数f（x）的定义域为［-1，1］，

思路分析2：通过对函数f（x）求导，结合导函数为零确定函数的极值，亦即最值，从而建立相应的方程，进而结合方程的求解来确定参数的所有值问题.只是求导较为烦琐，运算要细心.

解法2（导数法2）：对函数f（x）求导可得

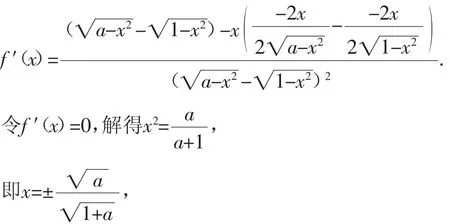
思路分析3：通过对函数f（x）奇偶性的判定，结合奇函数的性质确定最值范围，通过对函数f（x）求导，结合导函数为零确定函数的极值，亦即最值，从而建立相应的方程，进而结合方程的求解来确定参数的所有值问题.

解法3（导数法3）：由于f（x）为奇函数，

思路分析4：通过对函数f（x）奇偶性的判定，结合奇函数的性质确定最值范围，利用平面向量的构造，结合数量积的性质建立相应的不等式，利用不等式的性质确定函数取最值时等号成立的条件，结合方程的求解来确定参数的所有值问题.

解法4（平面向量数量积法）：由于f（x）为奇函数，

思路分析5：通过对函数f（x）奇偶性的判定，结合奇函数的性质确定最值范围，利用柯西不等式及不等式的性质确定函数取最值时等号成立的条件，结合方程的求解来确定参数的所有值问题.

解法5（柯西不等式法）：由于f（x）为奇函数，

思路分析6：通过对函数f（x）奇偶性的判定，结合奇函数的性质确定最值范围，利用三角形的构造，通过三角形面积公式的转化，结合三角函数的图像与性质来确定函数取最值时等号成立的条件，结合方程的求解来确定参数的所有值问题.

解法6（三角形面积法）：由于f（x）为奇函数，

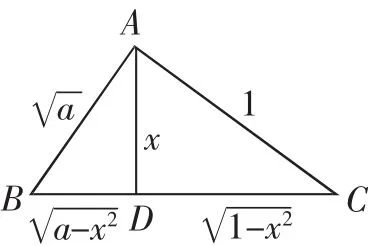
图1

分析：解法1、2、3利用导数法来处理，是解决函数最值问题中最常见的思维方式，只是解法1结合参数加以分类讨论，过程烦琐，操作起来比较繁杂；而解法2直接求解；解法3先探讨函数的性质后再求导，总的来说，求导过程比较复杂，运算量比较大；解法4中根据函数解析式的特点，通过平面向量的构造并结合数量积的性质，使问题得以转化和解决；解法5中也是根据函数解析式的特点，从柯西不等式的角度入手，同样可以达到解决问题的目的；解法6构造巧妙，利用三角形面积公式并结合三角函数的图像与性质来确定最值，构造直观，只是不容易想到.

通过深入观察，多向思维，巧妙拓展，看似平常的一道函数的最值问题，却独具匠心，可以从不同角度、不同方式加以切入，多知识点交汇与融合，充分体现命题者“以能力为主”、“在知识网络的交汇点处设计试题”的命题本色，以平常心考查能力与数学素养.H