锚杆钻机机械臂设计及动力学仿真分析
2018-07-23黄庆学孟文俊马立峰
张 君,黄庆学,孟文俊,马立峰
(1.太原科技大学 a.机械工程学院,b.太原重型机械装备协同创新中心,太原 030024;2.中国煤炭科工集团太原研究院有限公司,太原 030006)
煤矿以井工开采为主,需要在井下开掘大量巷道。为了保证巷道畅通和围岩稳定,迫切需要安全、高效和快速的巷道支护施工技术。煤矿巷道支护经历了木支护、砌碹支护、型钢支护到锚索联合支护的漫长过程[1]。国内外的实践经验表明,锚杆支护是煤巷经济、有效的支护技术。尽管目前锚杆支护已开始使用车载锚杆钻机,钻孔工艺已实现液控自动运行,但是拆、装钻杆,上锚杆和药卷,铺网等工序仍需人工手动作业,操作人员体力消耗较大;此外可呼吸性粉尘、铺网时操作人员处于空顶区等危险因素严重威胁着他们的生命安全。为了提高锚护速度,改善操作人员安全性,减少其工作强度,就必须实现拆、装钻杆,上锚杆和药卷,铺网等工序动作的全自动化。机械臂代替人工的简单且重复性工作已经是该行业的发展趋势,同时机器人学的进步和应用是本世纪自动控制最有突出的成就,是当代工业领域最高意义的自动化[2-5]。文献[6]指出在机器人结构设计中均基于pieper法则,各大机器人公司普遍采用关节坐标机器人来设计工业机器人。DAHLQUIP,KAUFMANN et al[7-8]对机器人手腕做了大量的研究,并且申请了相关专利。文献[9]中指出在工业机器人机构学中,国内外学者大多数采用D-H坐标系来建立机器人的运动模型,通过结构设计参数来确定工业机器人各关节连杆的D-H参数,依据机器人的运动学方程来确定机器人的运动状态。FENTON et al[10]用旋量法与矢量积法相结合来求解雅克比矩阵,该解法对自由度较高的机器人更加有效。PIPER et al[11]提出在实际运算中较为实用的方法——旋量法和微分法结合求解雅克比矩阵。文献[12-13]表明在机器人动力学研究中,拉格朗日方程法可以通过系统系统能量的变化推导串联型机械人的动力学方程,同时也可以通过计算机辅助编程,解决高自由度冗杂参数,轻松求解动力学方程。文献[14-17]指出市面上动力学软件都是基于拉格朗日方法建立模型的。MURPHY et al和JAIN et al建立了PUMA56的动力学模型,为后学研究提供参考。STAICU et al[18-19],TSAI et al[20]应用虚工原理对Bendix手腕关节计算出了驱动力矩随时间变化的曲线,提供了伺服电机的选型。CHEN[21]采用了拉格朗日方法建立了柔性机械臂的动力学模型。上述文献都没有提到井下锚杆钻车机械臂的设计和动力学仿真分析的关键点和难点,参考资料较少,存在一定的空白点。为了满足煤炭企业锚杆支护工作强度,提高支护操作安全性、减人增效等的需求,追踪支护设备国际先进水平,非常有必要开展锚杆钻机机械臂的设计工作和动力学仿真工作。为实现锚杆钻车的全自动化、智能化提供理论支撑和技术储备。
根据锚杆钻车机械臂的实际需求建立了三维立体模型,并且在机械臂满足运动学理论的前提下,用拉格朗日方法推导出机械臂的动力学方程。为了考察锚杆钻机机械臂在实际工作状况下是否能满足受力需要,是否对整机的稳定性有一定的影响,故将机械臂的三维虚拟样机模型导入多体动力学软件ADAMS中进行不同工况下进行动力学仿真,去验证在4个极限姿态下,机器臂的受力情况均能满足实际需求。最后选取最恶劣的工况,运用仿真软件Ansys Work Bench对伸缩臂承受的扭转力较大处进行静强度校核,以保证机械臂的强度要求。
1 机器臂设计
机械臂三维模型均在Solidworks2010中建立,整个机构的构成如图1所示。该机械臂由底座、升降油缸、回转杆、升降油缸II、伸缩臂套筒、回转马达及减速器等构成,每个执行机构都可以单独安装并且完成相应的测试实验。该机械臂的姿态变化是靠两个不同的油缸伸缩动作来实现的,包括两臂的各自长度和相对角度的变化,锚杆臂端能实现准确空间位姿定位和点对点的高效工作。升降油缸安装在回转杆和底座之间,升降油缸的伸缩实现了回转杆之间角度的变化。升降油缸II安装在伸缩套筒和回转杆之间,升降油缸II的伸缩实现了伸缩臂套筒与回转杆之间相对角度的变化。伸缩臂套筒主要由内套筒和外套筒两部分组成。自动臂架和伸缩臂套筒之间设有回转马达和减速器,用来实现伸缩臂套筒与回转马达和减速器的相对角度的变化。

图1 机械臂三维模型Fig.1 3d mechanical arm model
2 机械臂动力学方程推导
在推导机械臂动力学方程前,根据图1做适当的简化,即回转杆为连杆1,伸缩臂套筒为连杆2.回转杆与底座之间的角度为θ1,回转杆与伸缩臂套筒之间的角度为θ2.如图2所示,连杆d1和d2的转角分别为θ1和θ2,关节2和3的相应力矩分别是M1和M2,连杆d1和d2的质量分别是m1和m2.依据拉格朗日方程建立机械手动力学方程,推导如下:
E=EK-EP.
(1)
(2)


图2 机械臂数学简化模型Fig.2 Mechanical arm simplified mathematical model
连杆1的动能和势能为:
(3)
EP1=-m1gd1cosθ1.
(4)
连杆2的动能和势能为:
(5)
EP2=-m2gd1cosθ1-m2gd2-cos(θ1+θ2) .
(6)
两个连杆的总动能和总势能分别为:
(7)
EP=EP1+EP2=-(m1+m2)gd1cosθ1-m2gd2cos(θ1+θ2) .
(8)
将两个连杆的总动能和总势能的表达式式(7)-式(8)代入拉格朗日推导式中得:

(9)
对E求偏导数和导数:

(10)

(11)
(12)
(13)
(14)
(15)
将相应各导数和偏导数都代入拉格朗日方程动力学方程中得:

(16)
(17)
3 机械臂动力学仿真
机器臂动力学方程推导是虚拟样机仿真实验的前提和基础。目前多刚体建模方法主要有2种,即矢量力学分析法和分析力学方法[22-23]。分析力学方法以拉格朗日方程为主,该方法采用广义坐标系。ADAMS全名为机械系统动力学自动分析,该软件是美国机械动力公司开发的虚拟样机分析软件,其建模过程基于拉格朗日方法[24-31]。ADAMS从20世纪90年代进入中国以来,广泛应用于机械制造、航空航天、铁道、兵器、石油化工、汽车交通等领域。运用虚拟样机技术,可以大大简化机械产品的设计开发过程,大幅度缩短产品开发时间和降低产品费用,能够提高产品的系统性能,获得最优化的设计产品。机械臂模型中的各个零件特性参数是根据物理样机实际设计需要设置的,对各关节施加相应的运动约束副,并观察各连杆在运动极限状态下的力矩变化,检验机械臂设计的合理性。文中考察钻架在恒定外负载作用下,通过调整2个油缸之间的行程看是否能实现钻架在整个工作空间的所有工作位置,找到整机在不同姿态下打锚杆时的受力最恶劣工况,查看该工况下油缸受力变化及伸缩臂受力状况。
3.1 数字化模型建立
将锚杆钻车工作平台上不影响主体强度的部分零部件(包括钻架、销轴、挡销板、内套筒压板等)进行适当简化,压缩焊缝倒角和螺纹小孔(见图3).运用Solidworks三维软件对零部件进行虚拟装配和全局干涉检查,可以有效降低各零部件间的相互干涉和配合错误率,同时对零件赋予质量属性,避免了在ADAMS中进行模型修改等繁琐操作,确定各零部件装配无干涉后导入到ADAMS环境下,进行参数设置和约束条件施加。具体操作为在底座与大地之间施加固定副;底座与回转杆之间施加球副;钻架升降油缸和钻架升降油缸II的缸筒之间施加球副;回转杆与钻架升降油缸活塞杆之间施加球副;回转杆与伸缩臂外套筒之间施加球副;2个油缸缸筒与缸杆之间均施加平移副。在臂架上施加重力载荷;内套筒减速器安装板上施加远程力,作用点在钻箱中心,方向垂直向下,大小为3.5×104N.仿真时间4 s,仿真步长0.001.具体仿真参数设置如表1所示。

图3 输入模型Fig.3 Input model
3.2 仿真结果分析
仿真时间1 s时,钻架升降油缸完全伸出,钻架升降油缸II完全收缩,此时模型姿态见图4.从0~1 s的仿真过程中可以观察出升降油缸在逐渐伸出过程中,整体模型的受力变化。

表1 仿真设置Table 1 Simulation settings

图4 仿真时刻1 s时模型姿态及受力情况Fig.4 Simulation time 1s model attitude and force situation
仿真时间2 s时,钻架升降油缸完全伸出,钻架升降油缸II也完全伸出,此时模型姿态如图5所示。从1~2 s的仿真过程中可以观察出当钻架升降油缸保持最长、钻架升降油缸II逐渐伸出的过程中,整体模型的受力变化。仿真时刻3 s时,钻架升降油缸完全收缩,钻架升降油缸II仍完全伸出,此时模型姿态如图6所示。从2~3 s的仿真过程中可以观察出当钻架升降油缸II保持最长,同时钻架伸缩油缸逐渐收缩过程中,整体模型的受力变化。
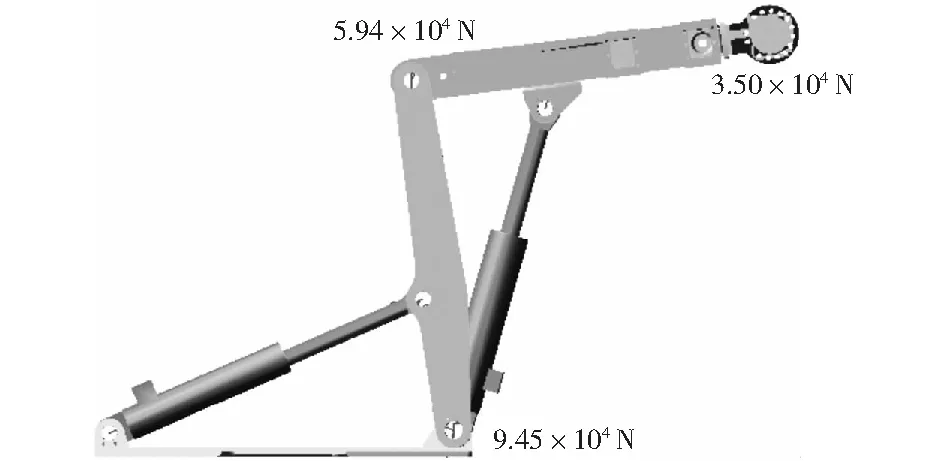
图5 仿真时刻2 s时模型姿态及受力情况Fig.5 Simulation time 2 s model and stress distribution
仿真时间4 s时,钻架升降油缸完全收缩,钻架升降油缸II也完全收缩,此时模型姿态见图7.从3~4 s的仿真过程中可以观察出当钻架升降油缸保持最短、钻架升降油缸II逐渐收缩的过程中,整体模型的受力变化。
由图8仿真结果表明,钻架升降油缸在3 s时受力最大,峰值达到20.8×104N.钻架升降油缸II在初始时刻受力最大,峰值达到18.4×104N.

图6 仿真时刻3 s时模型姿态及受力情况Fig.6 Simulation time of 3 s model attitude and force situation

图7 仿真时刻2 s时模型姿态及受力情况Fig.7 Model attitude and force situation of 2 s at simulation time

图8 仿真过程中钻架升降油缸和钻架升降油缸II受力变化情况Fig.8 In the process of simulation drill rack lifting oil cylinder and drill lifting oil cylinder II stress changes
由图9仿真结果表明,伸缩臂外套筒在3 s时受弯矩最大,峰值达到2.19×107N·mm.伸缩臂受力最大时刻为初始时刻,峰值达到1.67×105N·mm.机械臂油缸受力变化仿真结果如表2所示。
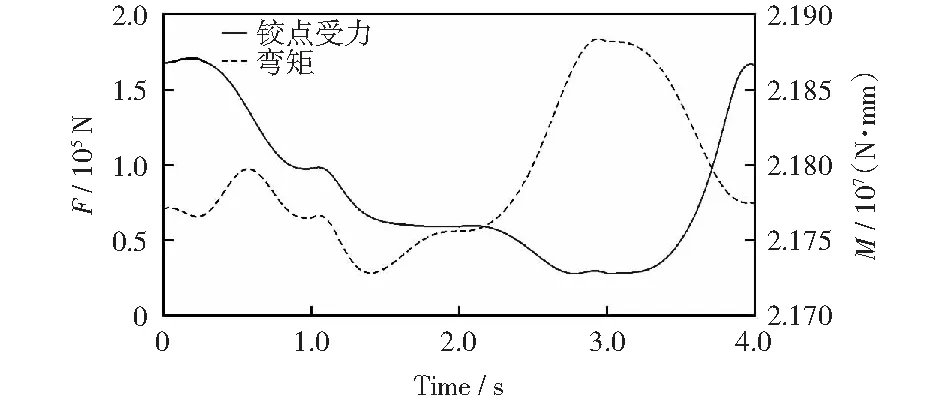
图9 仿真过程中伸缩臂外套筒下端铰点的受力和弯矩图Fig.9 In the simulation process, the force and bending moment of the lower end of the sleeve of the telescopic arm are shown
3.3 伸缩套筒强度分析
由于在仿真时刻3 s时,升降油缸受力超过该油缸的许用极限抗压力1.9×105N,故需进一步考察作用3.5×104N外力下产生的扭矩对伸缩套筒强度的影响。将三维模型导入Ansys Work Bench环境中进行仿真。输入模型及描述,将伸缩臂上不影响主体强度的部分零部件进行适当简化,压缩焊缝倒角和螺纹小孔。设置材料属性参数,弹性模量为2×105MPa,泊松比为0.3;采用国际标准单位制单位;网格划分单元类型为Solid;采用以六面体为主的网格单元,网格大小为0.010 m;内套筒筒体和与内套筒接触的压块网格局部细化,细化大小为0.005 mm.将外套筒后端铰点及下侧油缸铰点固定作为支撑工况的边界条件;在减速器安装面施加远程力及钻架自重力,远程力作用点位于钻架钻箱中心处,大小为3.5×104N,用来模拟钻架打钻力。内套筒与8个压块之间施加摩擦系数0.2.仿真计算结果表明,支撑工况下的伸缩臂套筒最大应力为619.5 MPa,最大值出现负载一侧的竖直压块上,应力云图如图10所示。

表2 机械臂油缸受力变化仿真结果Table 2 Mechanical arm dynamics simulation results

图10 伸缩臂套筒应力Fig.10 Telescopic arm sleeve stress
由图11可知,伸缩臂套筒的最大变形为4.1 mm,最大值出现在内套筒上位于负载一侧的减速器安装面上。

图11 伸缩臂套筒变形Fig.11 Deformation of telescopic boom sleeve
由图12可知,外套筒受力最大为445.5 MPa,位置在下侧油缸耳座根部焊缝交叉点处。该处存在一定的应力集中。

图12 外套筒受力Fig.12 Outer sleeve force
由图13可知,内套筒受力最大为410 MPa,位置为内部油缸耳孔外沿处。该极值为一个尖点,存在应力集中。抛开尖点,其他部位最大应力为315.9 MPa.

图13 内套筒受力Fig.13 Inner sleeve force
由图14可知,8块内套筒压板受力不均匀,最大受力为靠近负载一侧的竖压板,极值为619.5 MPa,位置为与内套筒接触的边线上一点。该极值为一个点,存在应力集中。抛开该点,其他部位最大应力为390 MPa.由计算结果分析可知,当伸缩臂在3.5×104N外力作用下扭转时,受力较大的零部件为内套筒压块和内套筒。伸缩套筒受扭静强度仿真结果如表3所示。由于伸缩臂在动力学仿真3 s时承受的扭转力较大,通过对其进行扭转静强度校核,仿真结果表明伸缩套筒受扭静强度满足设计要求。

图14 内套筒压板受力Fig.14 Inner sleeve pressure plate
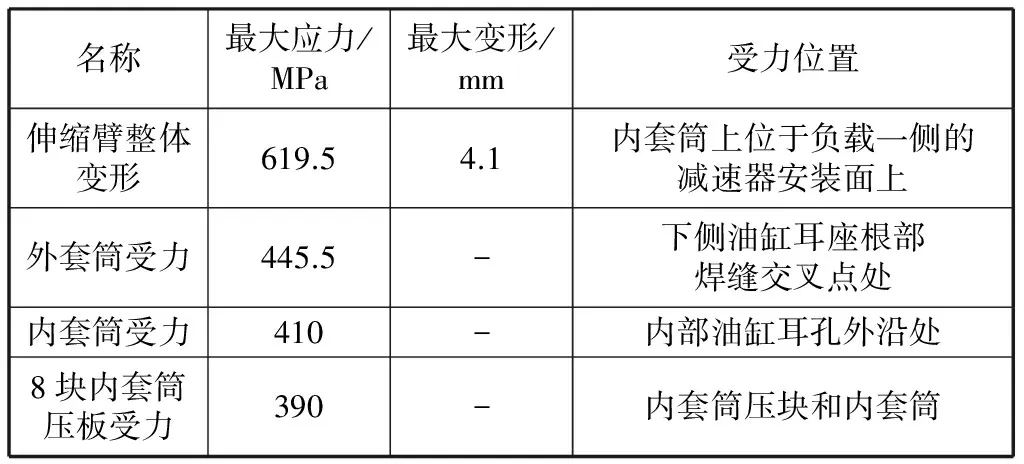
表3 伸缩套筒受扭静强度仿真结果Table 3 Simulation results of torsional static strength of telescopic sleeve
4 结论
1) 针对锚杆钻机机械臂设计及机械臂油缸动力学分析问题展开了研究。基于机器臂设计运动学理论,推导出锚索钻机机械臂动力学方程。
2) 完成了机器臂的虚拟样机模型的建立和与多体动力学Adams软件的无缝链接,进行了动力学仿真,观察在4个极限姿态工况下机器臂油缸受力的情况。结果表明,在时刻3 s时,钻架升降油缸完全收缩,钻架升降油缸II仍完全伸出,此时钻架升降油缸在3 s时受力最大,峰值达到2.08×105N.
3) 由于在仿真时刻3 s时,升降油缸受力超过该油缸的许用极限抗压力1.9×105N,故需要运用Ansys Work Bench对伸缩臂承受扭转力较大处进行扭转静强度校核,才能满足机械臂动力学要求。
