LONG-TIME DYNAMICS OF THE STRONGLY DAMPED SEMILINEAR PLATE EQUATION IN RN∗
2018-07-23AzerKHANMAMEDOVSemaYAYLA
Azer KHANMAMEDOVSema YAYLA
Department of Mathematics,Faculty of Science,Hacettepe University,Beytepe 06800,Ankara,Turkey
E-mail:azer@hacettepe.edu.tr;semasimsek@hacettepe.edu.tr
Abstract We investigate the initial-value problem for the semilinear plate equation containing localized strong damping,localized weak damping and nonlocal nonlinearity.We prove that if nonnegative damping coefficients are strictly positive almost everywhere in the exterior of some ball and the sum of these coefficients is positive a.e.in Rn,then the semigroup generated by the considered problem possesses a global attractor in H2(Rn)×L2(Rn).We also establish the boundedness of this attractor in H3(Rn)×H2(Rn).
Key words Wave equation;plate equation;global attractor
1 Introduction
In this article,our main purpose is to study the long-time dynamics(in terms of attractors)of the plate equation

with initial data
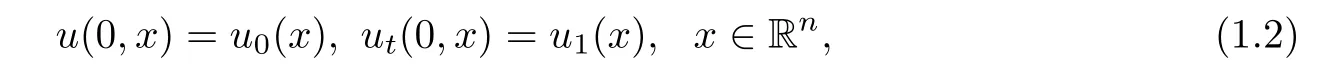
where γ >0, λ >0,h ∈ L2(Rn)and the functions α (·), β (·),f(·),and g(·)satisfy the following conditions:

The problem(1.1)–(1.2)can be reduced to the following Cauchy problem for the first order abstract differential equation in the space


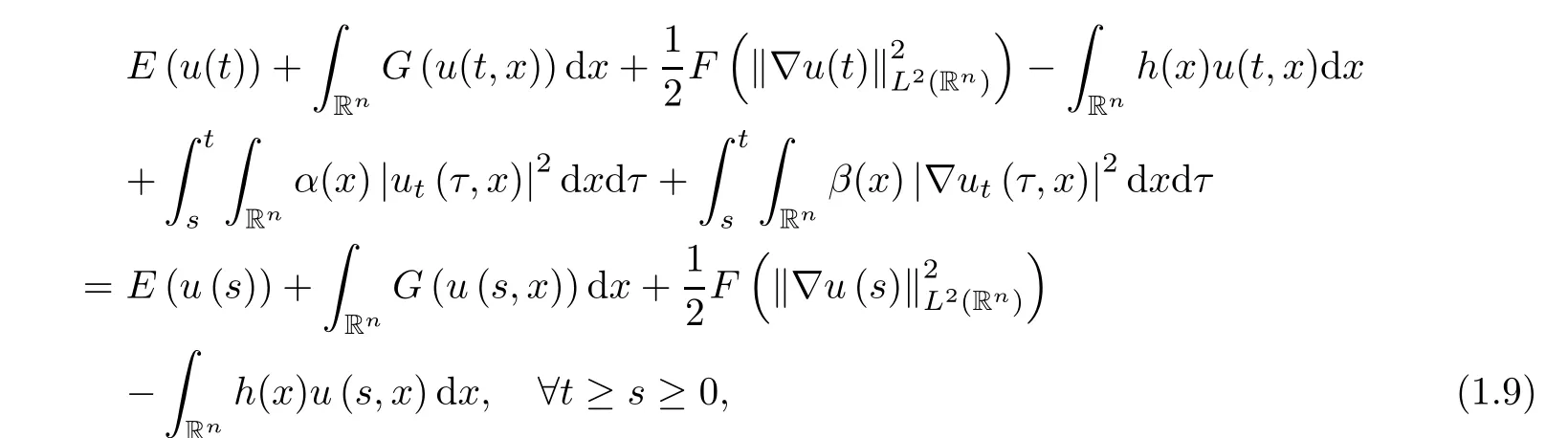
Thus,because of Theorem 1.1,the problem(1.1)–(1.2)generates a strongly continuous semigroup{S(t)}t≥0in H2(Rn)× L2(Rn)by the formula(u(t),ut(t))=S(t)(u0,u1),where u(t,x)is a weak solution of(1.1)–(1.2)with the initial data(u0,u1).
Attractors for hyperbolic and hyperbolic like equations in unbounded domains have been extensively studied by many authors over the last few decades.To the best of our knowledge,the first works in this area were done by Feireisl in[3,4],for the wave equations with the weak damping(the case γ=0,β≡0,and f≡1 in(1.1)).In those articles,the author,by using the finite speed propagation property of the wave equations,established the existence of the global attractors in H1(Rn)×L2(Rn).The global attractors for the wave equations involving strong damping in the form−∆ut,besides weak damping,were investigated in[5,6],where the authors,by using splitting method,proved the existence of the global attractors in H1(Rn)×L2(Rn),under different conditions on the nonlinearities.Recently,in[7],the results of[5,6]have been improved for the wave equation involving additional nonlocal nonlinear term in the formFor the plate equation with only weak damping and local nonlinearity(the case γ=1,β≡0,and f≡0 in(1.1)),attractors were investigated in[8,9],where the author,inspired by the methods of[10,11],proved the existence,regularity,and finite dimensionality of the global attractors in H2(Rn)×L2(Rn).The situation becomes more difficult when the equation contains localized damping terms and nonlocal nonlinearities.Recently,in[12,13],the plate equation with localized weak damping(the case β ≡ 0 in(1.1))and involving nonlocal nonlinearities asandwere considered.In these articles,the existence of global attractors was proved when the coefficient α(·)of the weak damping term is strictly positive(see[12])or,in addition to(1.3),is positive(see[13])almost everywhere in Rn.However,in the case when α(·)vanishes in a set of positive measure,the existence of the global attractor for(1.1)with β≡0 remained as an open question(see[12,Remark 1.2]).On the other hand,in the case when α ≡ 0 and even β ≡ 1,the semigroup{S(t)}t≥0generated by(1.1)–(1.2)does not possess a global attractor in H2(Rn)×L2(Rn).Indeed,if{S(t)}t≥0possesses a global attractor,then the linear semigroup??decays exponentially inand because of Hille-Yosida Theorem(see[1,Remark 5.4]),the necessary condition iR⊂ρ(A)holds.This condition is equivalent to the solvability of the equation(iµI−A)(u,v)=(y,z)in H2(Rn)×L2(Rn),for every(y,z)in H2(Rn)×L2(Rn)andµ∈R.Choosingand y=0,we haveand∆(∆u−iu)=z.If the last equation for every z∈L2(Rn)has a solution u∈H3(Rn),then denoting ϕ= ∆u−iu,we can say that the equation∆ϕ=z has a solution in H1(Rn),for every z∈L2(Rn).However,the last equation,as shown in[6],is not solvable in H1(Rn)for some z∈L2(Rn).Hence,the necessary condition iR⊂ρ(A)does not hold.Thus,in the case when α ≡ 0 and β ≡ 1,the problem(1.1)–(1.2)does not have a global attractor,and in the case when β ≡ 0 and α(·)vanishes in a set of positive measure,the existence of the global for(1.1)–(1.2)is an open question.
In this article,we impose conditions(1.3)–(1.5)on damping coefficients α(·)and β(·),which,unlike the conditions imposed in the previous articles dealing with the wave and plate equations involving strong damping and/or nonlocal nonlinearities,allow both of them to be vanished in the sets of positive measure such that in these sets,the strong damping and the weak damping complete each other.Thus,our main result is as follows.
Theorem 1.2Under the conditions(1.3)–(1.8),the semigroupgenerated by the problem(1.1)–(1.2)possesses a global attractor A in H2(Rn)×L2(Rn)and A=Mu(N).Here,Mu(N)is unstable manifold emanating from the set of stationary points N(for definition,see[14,359]).Moreover,the global attractor A is bounded in H3(Rn)×H2(Rn).
The plan of this article is as follows:In the next section,after the proof of two auxiliary lemmas,we establish the asymptotic compactness of{S(t)}t≥0in the interior domain.Then,we prove Lemma 2.4,which plays a key role for the tail estimate,and thereby we show that the solutions of(1.1)–(1.2)are uniformly(with respect to the initial data)small at infinity for large time.This fact,together with the asymptotic compactness in the interior domain,yields the asymptotic compactness of{S(t)}t≥0in the whole space,and by applying the abstract result on the gradient systems,we establish the existence of the global attractor(see Theorem 2.6).In Section 3,using the invariance of the global attractor,we show that it has an additional regularity.
2 Existence of the Global Attractor
We begin with the following lemmas.

where B(0,r)={x∈Rn:|x| ProofFirstly,we have where Applying[15,Corollary 4],it can be seen that the sequenceis relatively compact in??for every ε>0,T>0,and r>0.So, and then,for the first term on the right hand side of(2.1),we obtain Let us estimate the first term on the right hand side of(2.4).Using integration by parts,we have By the conditions of the lemma and the definition of fε,it follows that is bounded in W1,∞(0,∞).Then,considering(2.2)in(2.5),we get Taking into account(2.3),(2.4),and(2.6)in(2.1),we obtain which yields the claim of Lemma 2.1,as ε>0 is arbitrary. Lemma 2.2Assume that condition(1.7)holds.Also,let the sequencebe weakly star convergent inand the sequencebe bounded inThen,for every r>0 and φ ∈ L∞(B(0,r)), ProofWe have Let us estimate the first two terms on the right hand side of(2.7).Applying integration by parts,we get By the conditions of Lemma 2.2,we obtain for every ε>0 and T>0.Hence,taking into account(1.7),we get Then,passing to the limit in(2.8)and using(2.10),we obtain Now,for the last two terms on the right hand side of(2.7),considering(2.9),we get Hence,considering(2.11)–(2.12)and passing to the limit in(2.7),we obtain the claim of the lemma. ? Now,we can prove the asymptotic compactness of{S(t)}t≥0in the interior domain. Theorem 2.3Assume that conditions(1.3)–(1.8)hold and B is a bounded subset ofThen,every sequence of the formwheretk→∞,has a convergent subsequence in H2(B(0,r))×L2(B(0,r)),for every r>0. ProofWe will use the asymptotic compactness method introduced in[16].Considering(1.3),(1.6),(1.7),and(1.8)in(1.9),we have Because of the boundedness of the sequencein H2(Rn)×L2(Rn),by(2.13),it follows that the sequenceis bounded inThen,for any T ≥1,there exists a subsequencesuch that tkm≥T,and Now,taking into account(1.4)in(1.9),we find By(1.1),we have Taking into account(1.3),(1.6),(1.8),(1.9),(2.13),and(2.15)in(2.17),we obtain Now,by(1.1),we have Thus,considering(2.14),(2.15),and(2.18),and passing to the limit in(2.20),we obtain Then,taking into account(2.14),(2.15),(2.21),Lemma 2.1,and Lemma 2.2,and passing to the limit in(2.22),we find Thus,by the definition of vm,inequality(2.23)yields Passing to the limit as T→∞in(2.24),we obtain which gives Consequently,by passing to the limit asin(2.25),we deduce and To establish the tail estimate,we need the following lemma. Lemma 2.4Let conditions(1.3)–(1.6)hold and B be a bounded subset of H2(Rn).Then,for every ε>0,there exist a constant δ≡ δ(ε)>0 and functions ψε∈ L∞(Rn),ϕε∈ C∞(Rn),such that 0≤ ψε≤ min?1,δ−1β?a.e.in Rn,0≤ ϕε≤ 1 in Rn,supp(ϕε)⊂ {x ∈ Rn:α(x)≥ δ a.e.in Rn},and for every u∈B,where fδis the function defined in the proof of Lemma 2.1. ProofLet A0={x∈B(0,r0):α(x)=0}and??It is easy to see that Ak+1⊂Ak,and.Hence,So,for δ>0,there exists kδsuch that As Akδis a measurable subset of B(0,r0),there exists an open setsuch thatand Then,setting ϕδ:=1− ηδ,we haveand supp(ϕδ) ⊂ By(2.28)–(2.30),we obtain Now,by(1.5),it follows that Hence,by Lebesgue dominated convergence theorem,there exists λδ>0 such that which yields and consequently The last inequality,together with the differentiability of the function f,yields(2.27). ? Now,let us prove the following tail estimate. Theorem 2.5Assume that conditions(1.3)–(1.8)hold and B is a bounded subset of H2(Rn)× L2(Rn).Then,for any ε>0,there exist T ≡ T(B,ε)and R ≡ R(B,ε)such that for every t≥ T,r≥R,and ϕ ∈B. ProofLet(u0,u1) ∈ B and(u(t),ut(t))=S(t)(u0,u1).Multiplying(1.1)withintegrating the obtained equality over Rn,and taking into account(2.13),we get Now,let us estimate the last term on the left hand side of(2.33).By Lemma 2.4,we have Moreover,for the last term on the right hand side of(2.34),using the definition of fδand the properties of ψεand ϕε,we obtain Considering(2.34)and(2.35)in(2.33),we obtain Summing(2.36)and(2.37),applying Young inequality,and choosing ε and µ small enough,we obtain where ci(i=7,8)are positive constants.Denoting we get So,considering(2.39)in(2.38),we have Furthermore,applying Young inequality and taking into account(1.9),we have Therefore,considering(2.41)in(2.40),we get which completes the proof of Theorem 2.5. Now,we are in a position to prove the existence of the global attractor. Theorem 2.6Let conditions(1.3)–(1.8)hold.Then,the semigroup{S(t)}t≥0generated by the problem(1.1)–(1.2)possesses a global attractor A in ProofBy Theorem 2.3 and Theorem 2.5,it follows that every sequence of the formwhereand B is bounded subset ofhas a convergent subsequence in H2(Rn)×L2(Rn).As,by(1.6)and(1.8),the set N,which is the set of stationary points of{S(t)}t≥0,is bounded in H2(Rn)×L2(Rn),then to complete the proof,it is enough to show that the pair?S(t),H2(Rn)×L2(Rn)?is a gradient system(see[14]). Now,for(u(t),ut(t))=S(t)(u0,u1),let the equality hold,where Then,considering(1.3)and(1.9),we have for t≥0.Taking into account(1.5),from the above equalities,it follows that and consequently, for t≥0.So, We start with the following lemma. Lemma 3.1Let the condition(1.7)hold and K be a compact subset of H2(Rn).Then for every ε>0 there exists a constant Cǫ>0 such that for every u1,u2∈K. Thus,(3.2)and(3.3)give us(3.1).? Theorem 3.2The global attractor A is bounded in ProofLet ϕ ∈A.As A is invariant,there exists an invariant trajectory such that(u(0),ut(0))=ϕ(see[18,p.159]).Now,let us define Then,by(1.1),we get Multiplying(3.4)by vtand integrating the obtained equality over Rn,we find Taking into account Lemma 3.1 in the last inequality,we obtain for any ε>0.Moreover,by(2.13),we have Then,considering(3.6)in(3.5),we get Now,let us estimate the first term on the right hand side of(3.7).By(2.13)and(3.6),we have for any ε>0,where fεis the function defined in the proof of Lemma 2.1.Considering(3.8)in(3.7),we obtain Multiplying(3.10)and(3.11)by δ2and δ,respectively,then summing the obtained inequalities with(3.9),choosing ε >0 and δ>0 sufficiently small,and applying Young inequality,we obtain where As δ>0 is sufficiently small,there exist constants c>0, ec>0 such that Taking into account(3.13)in(3.12),we obtain which yields Passing to the limit as s→−∞ and considering(3.13),we get Using the definition of v,after passing to the limit as σ → 0 in the last inequality,we find Considering(3.14)in(1.1),we obtain Thus,the last inequality,together with(3.14),yields which completes the proof of Theorem 3.2.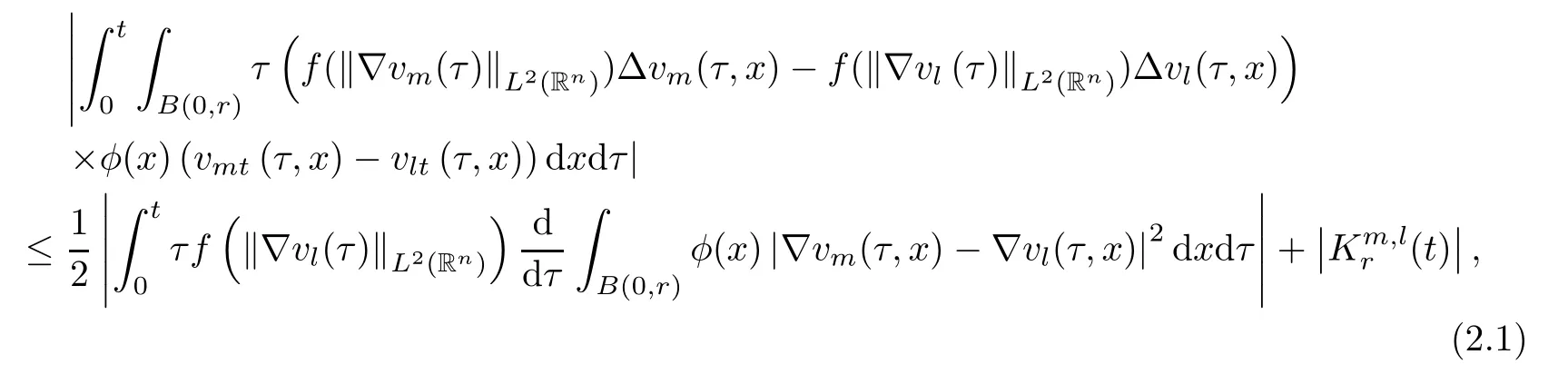
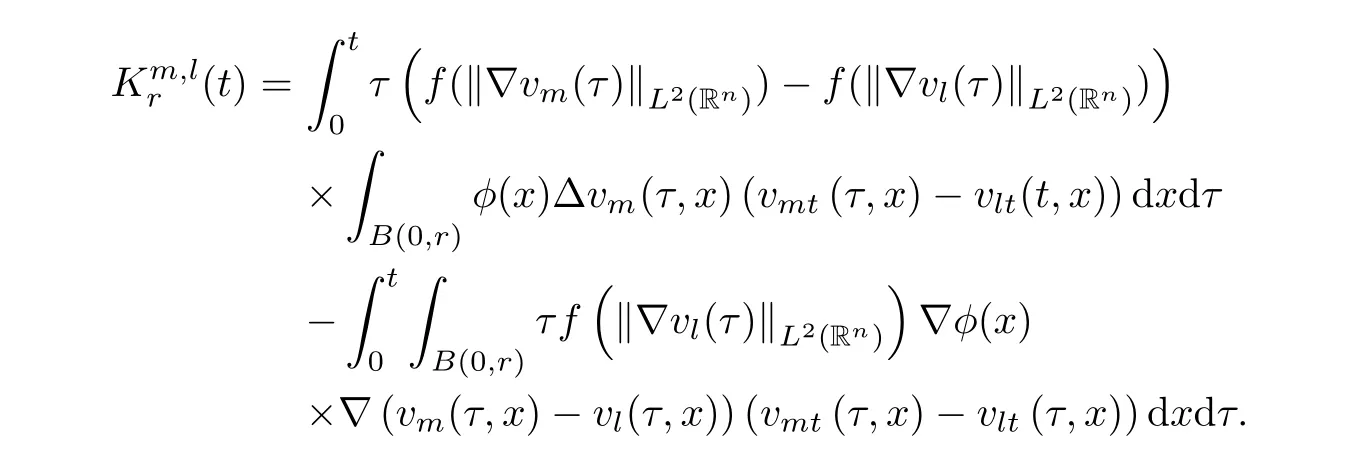
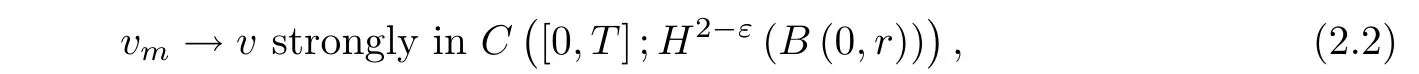
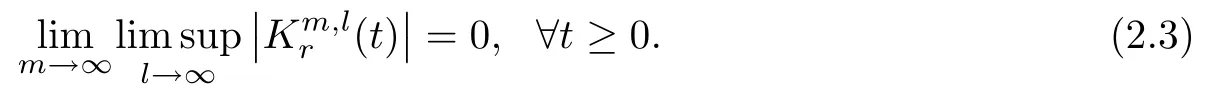

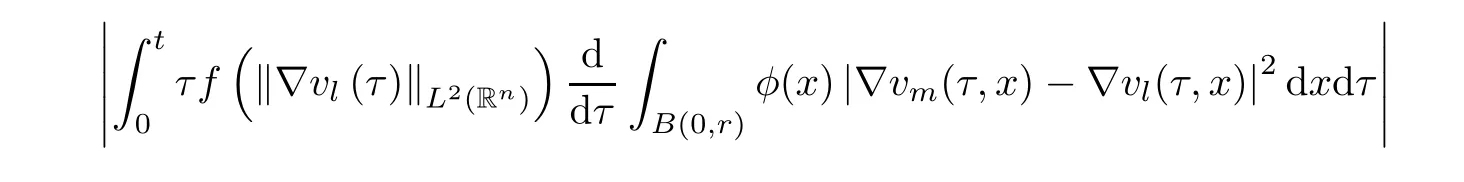
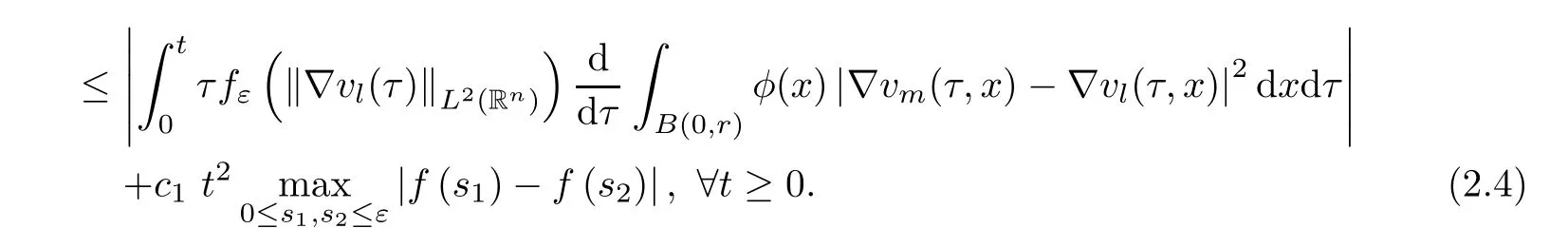

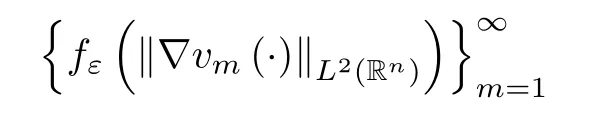



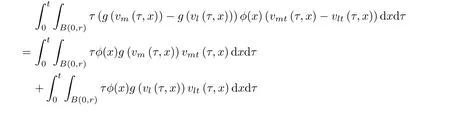
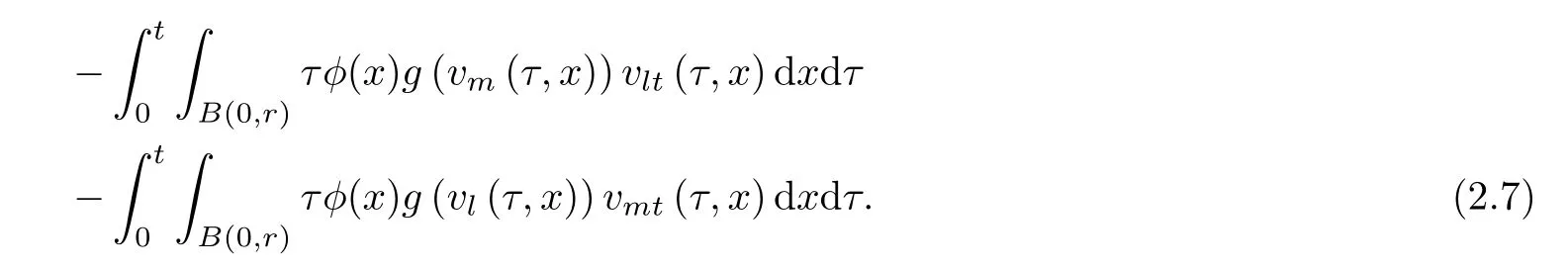
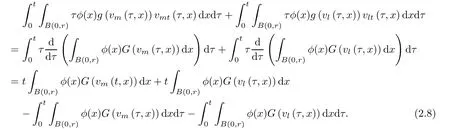
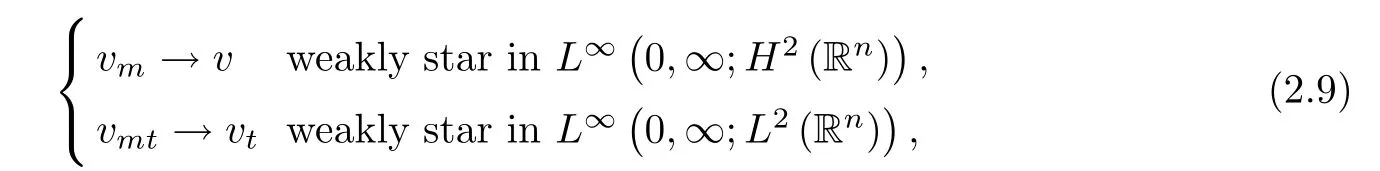
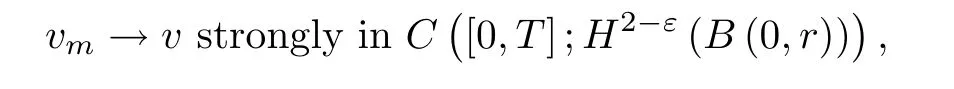
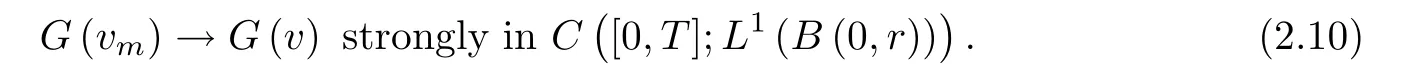




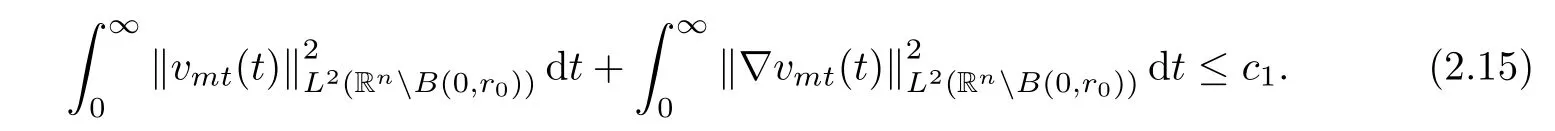
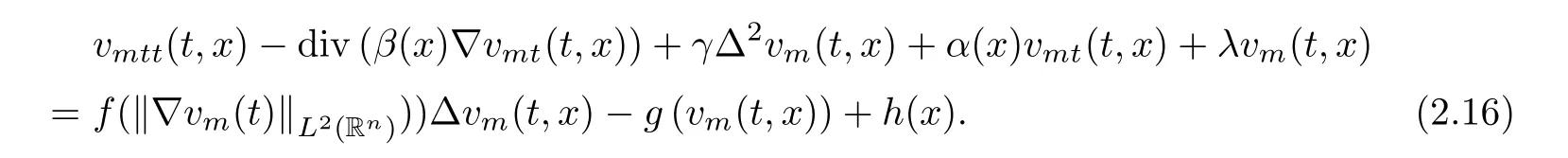
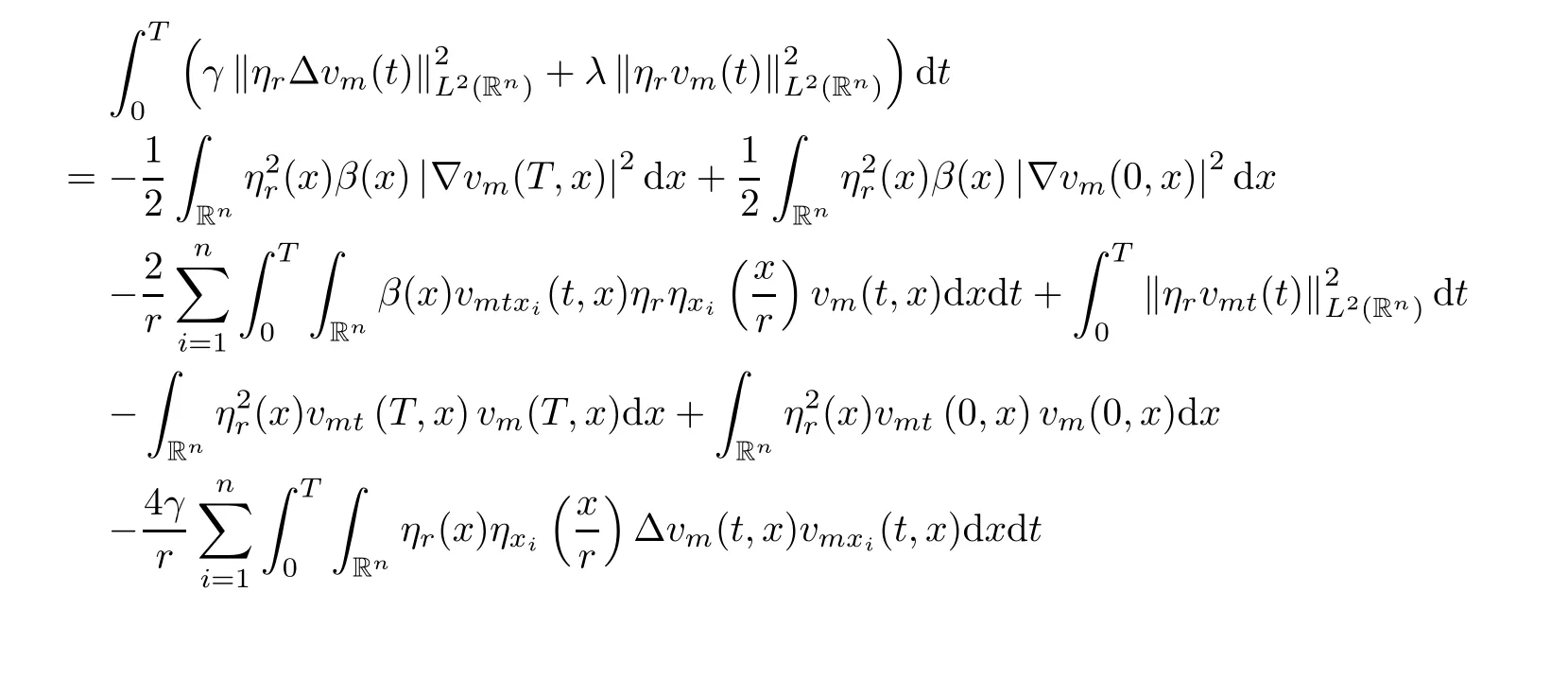
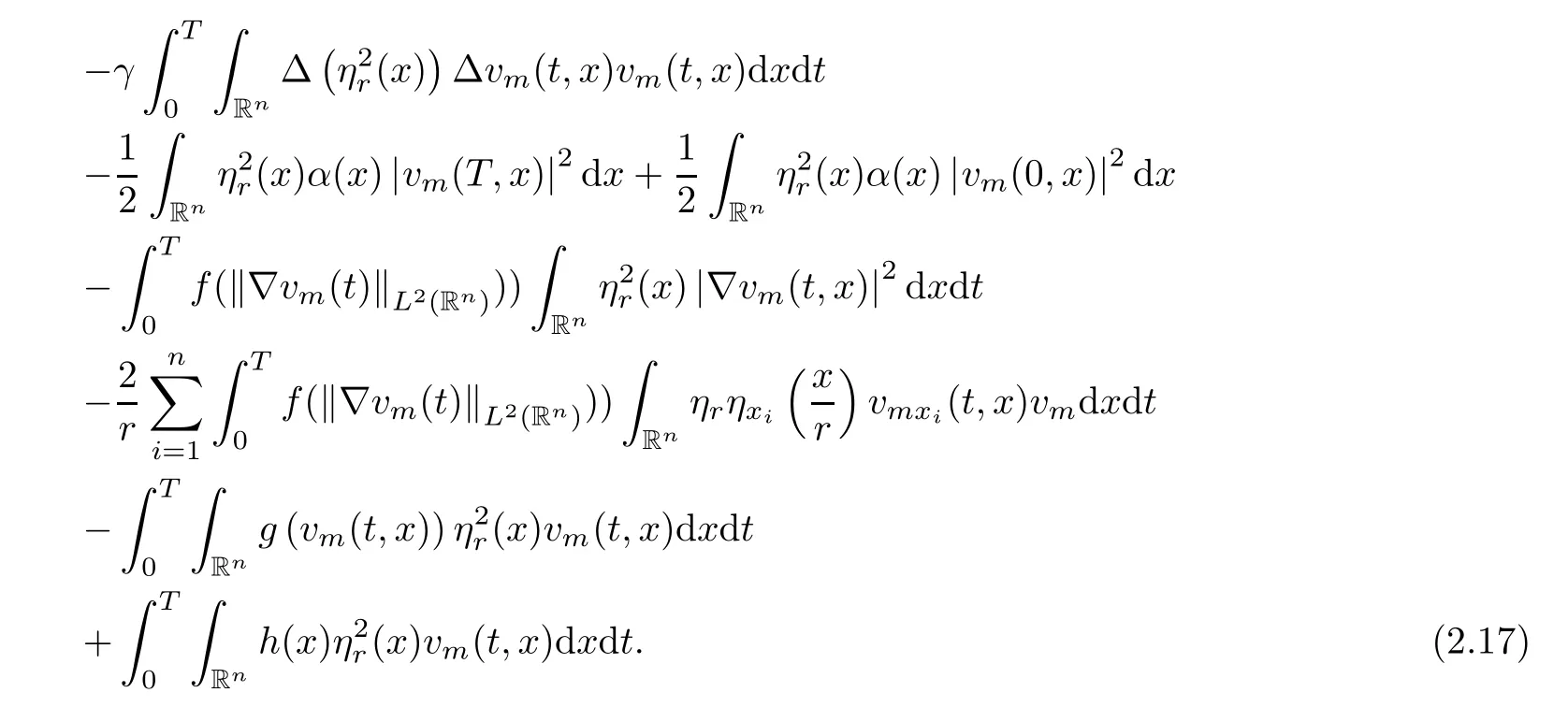









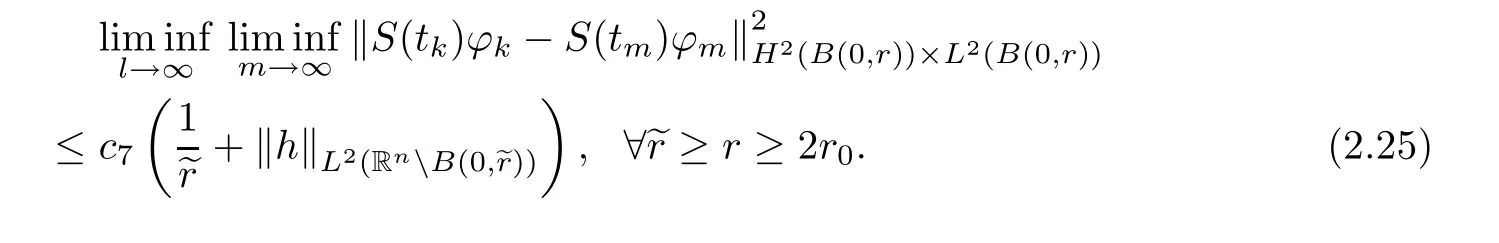

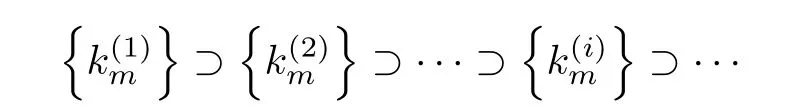
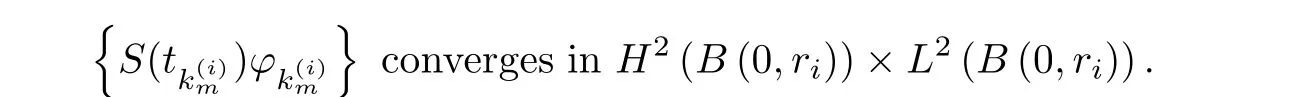
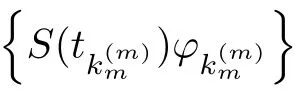




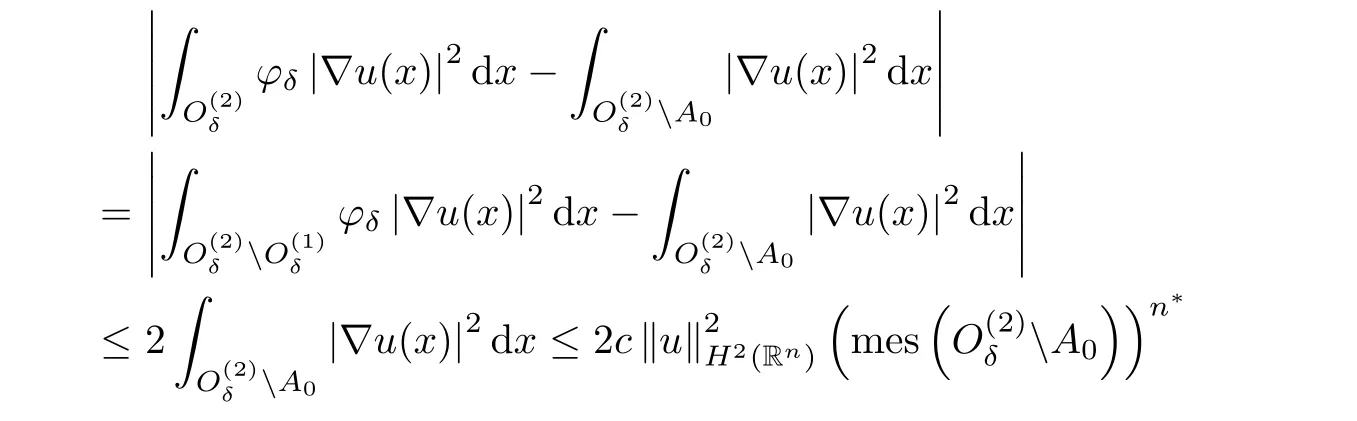

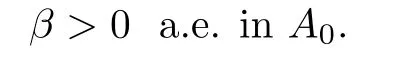
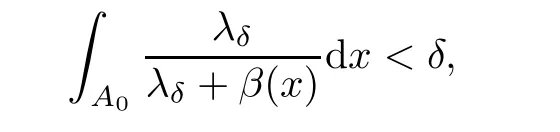
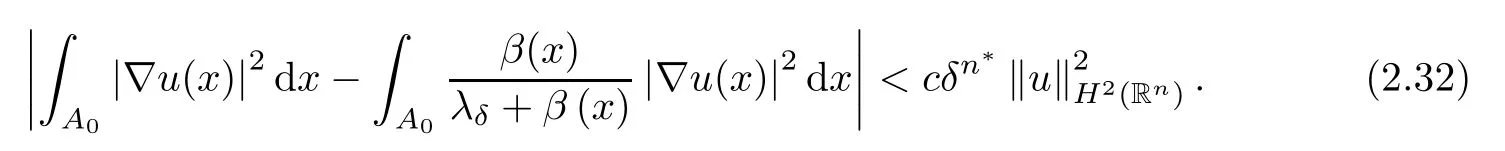
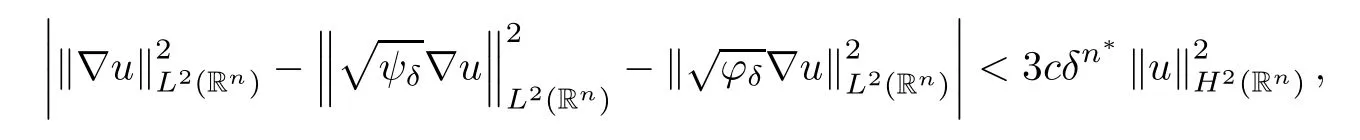
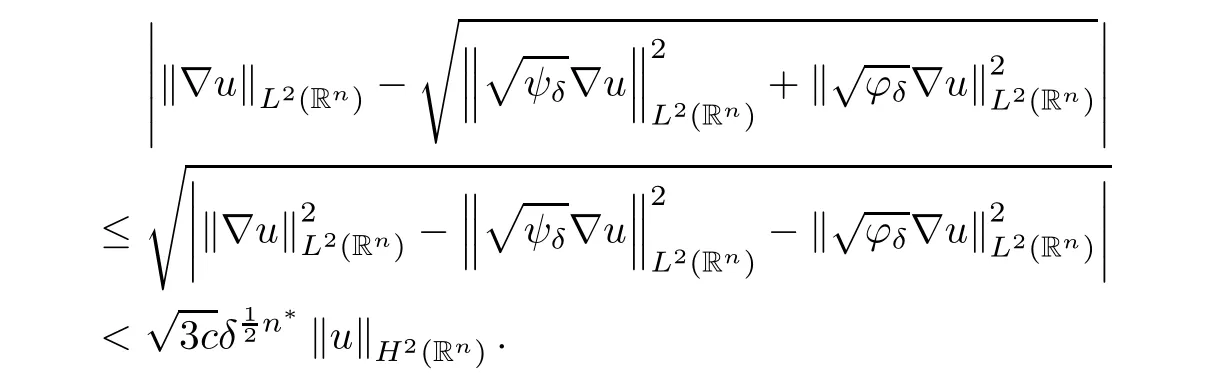
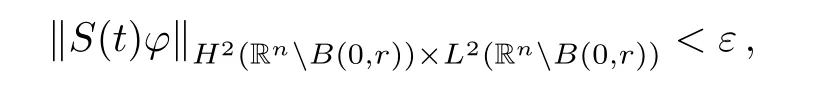
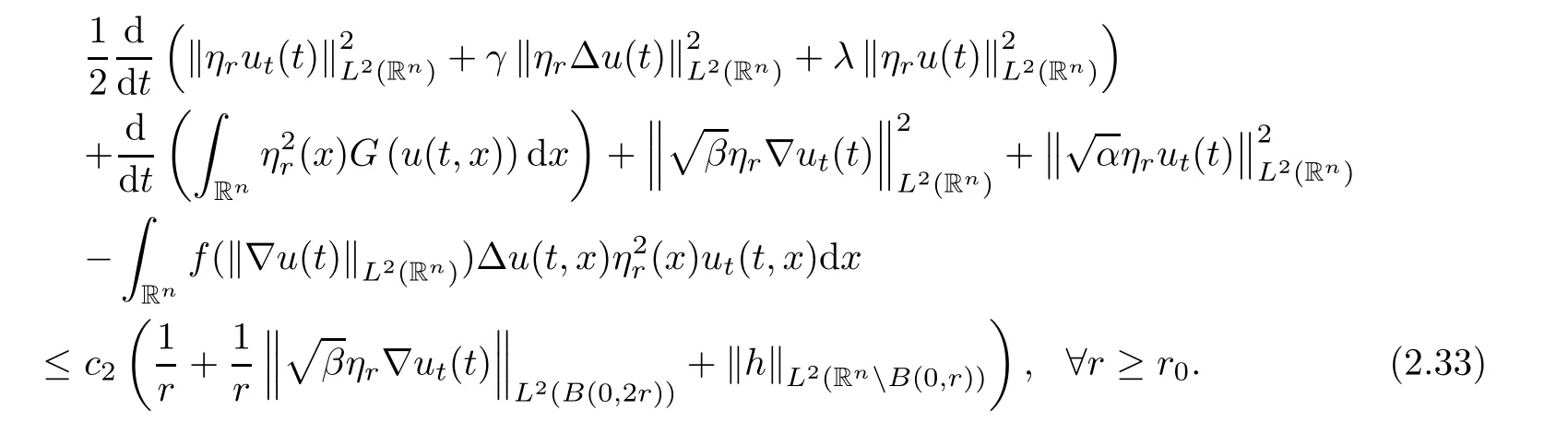
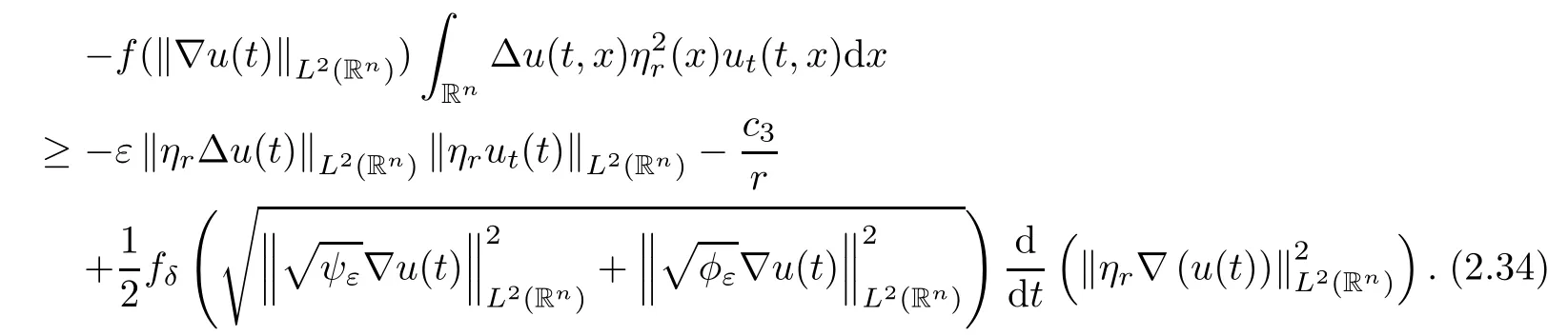


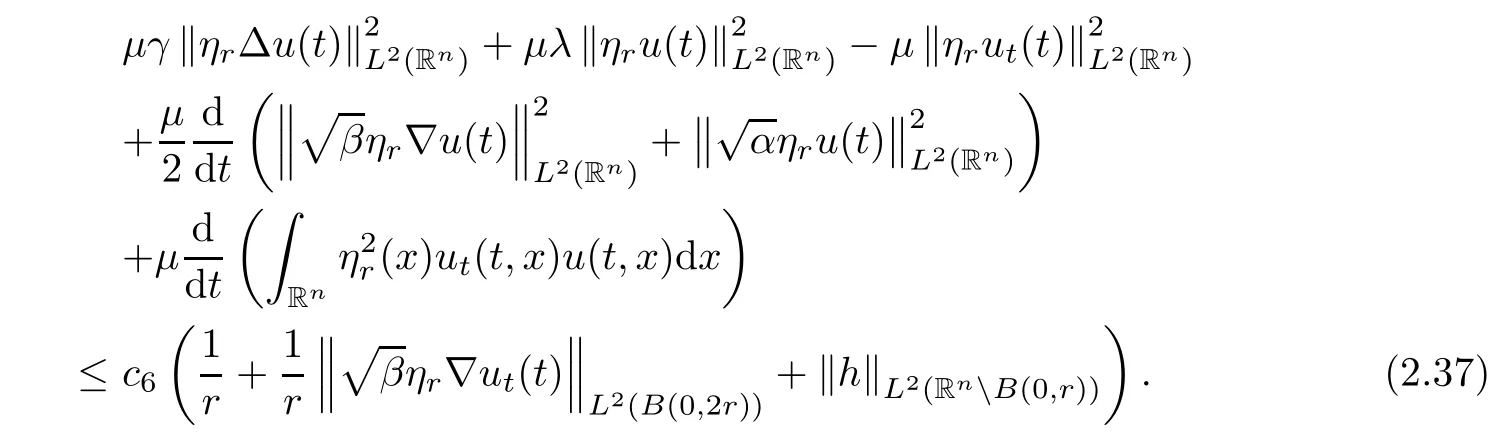
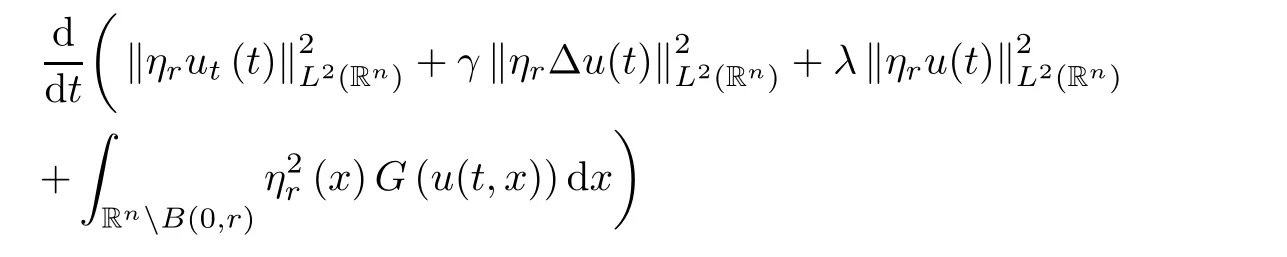

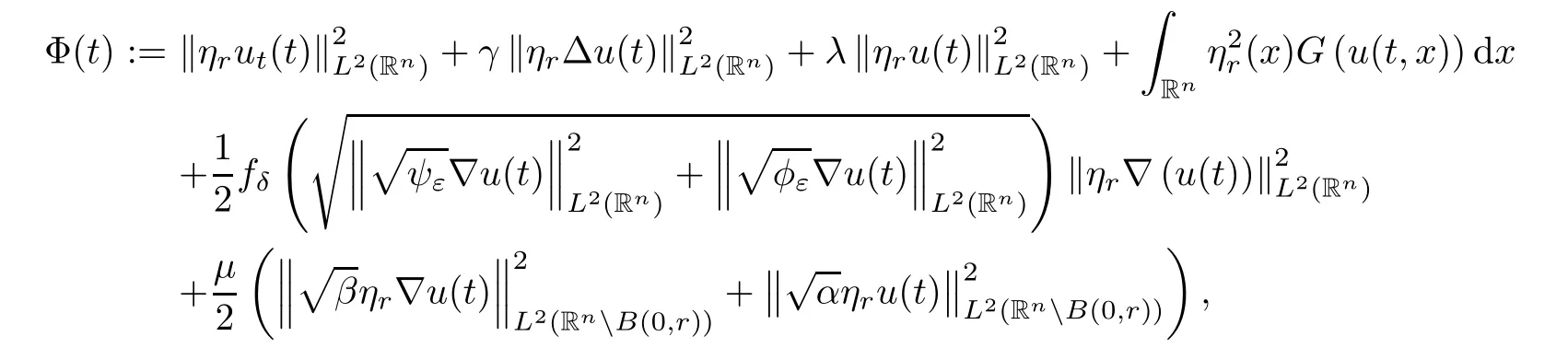

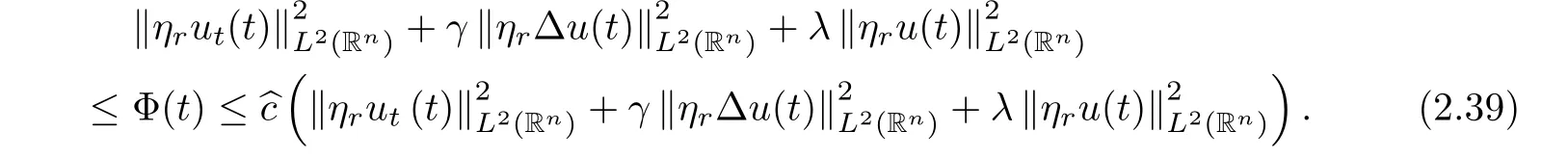
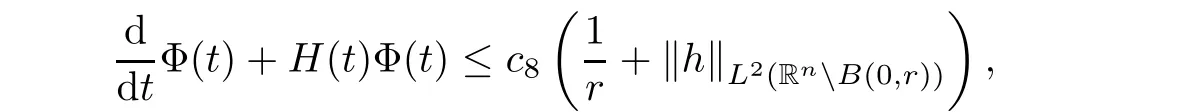
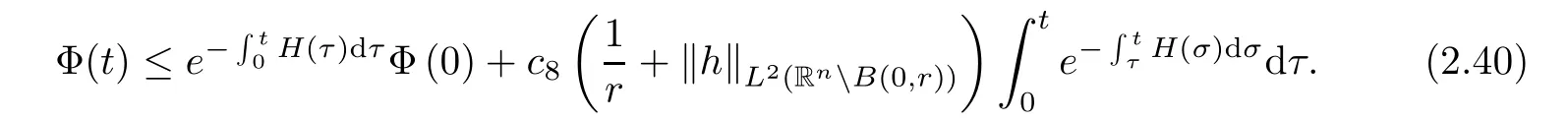

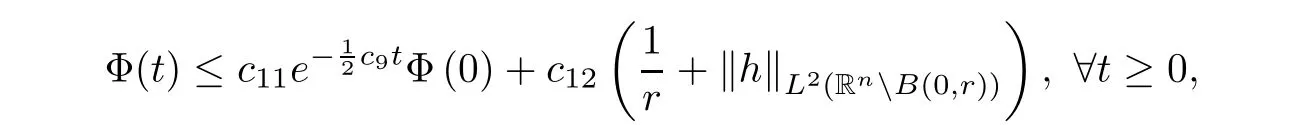


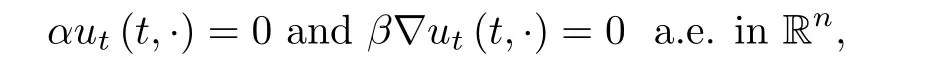
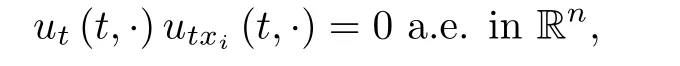

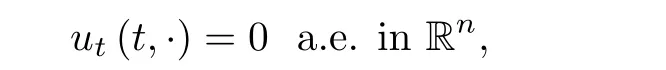

3 Regularity of the Global Attractor
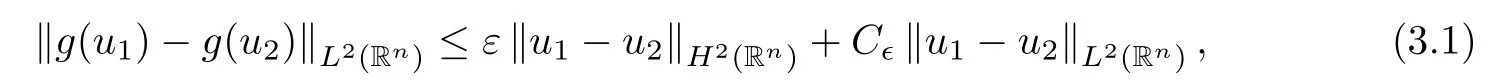

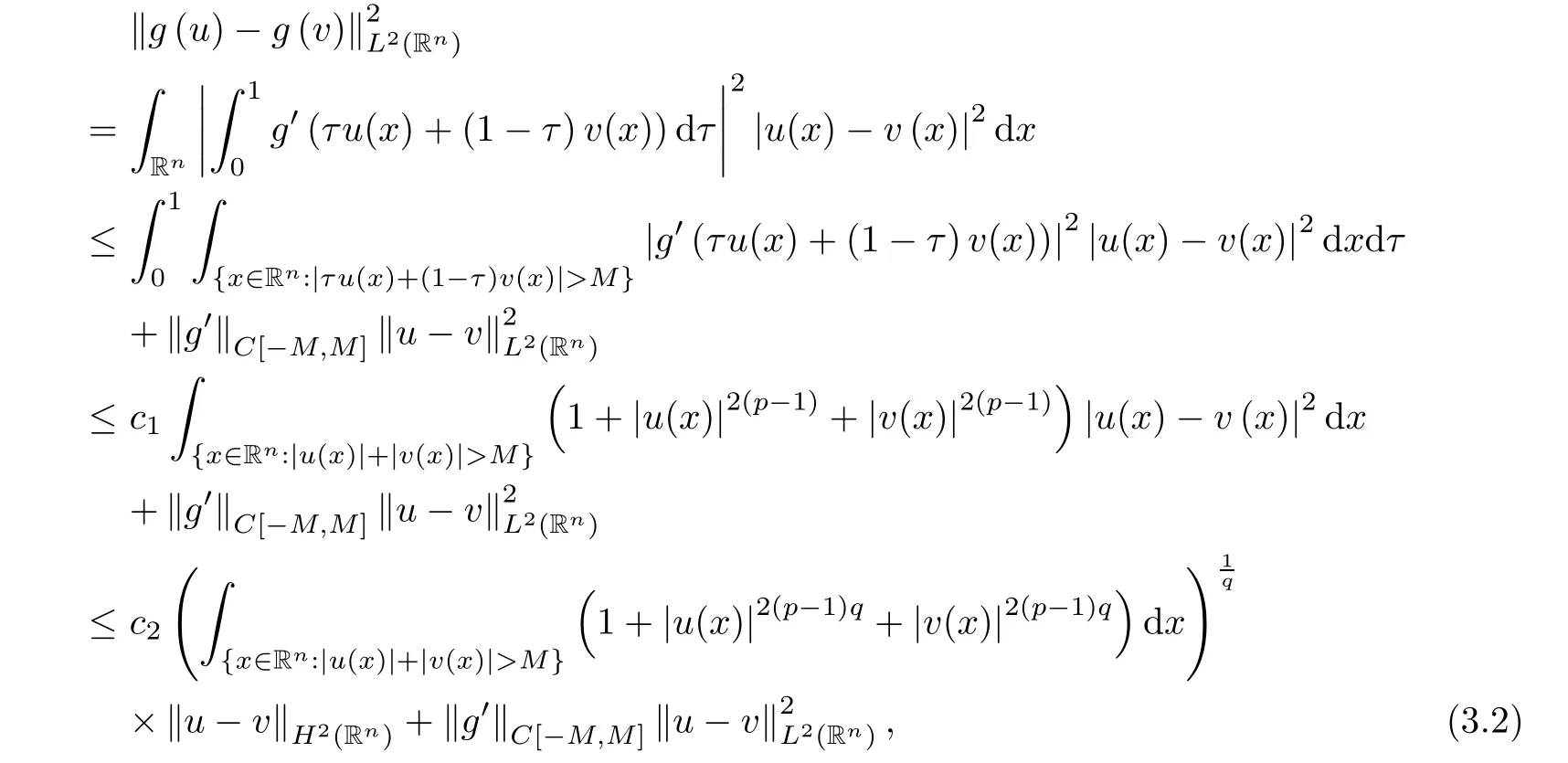
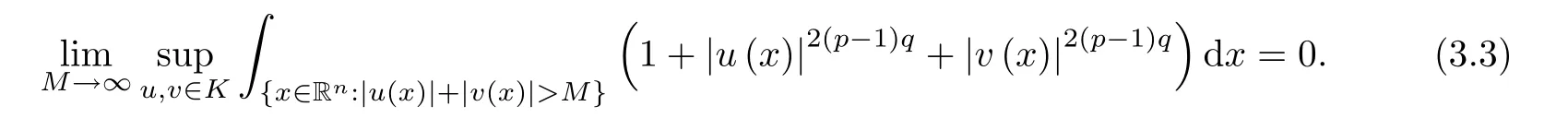
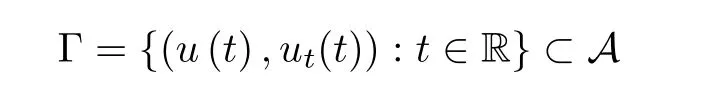
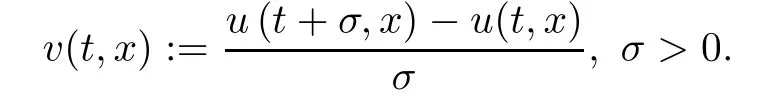
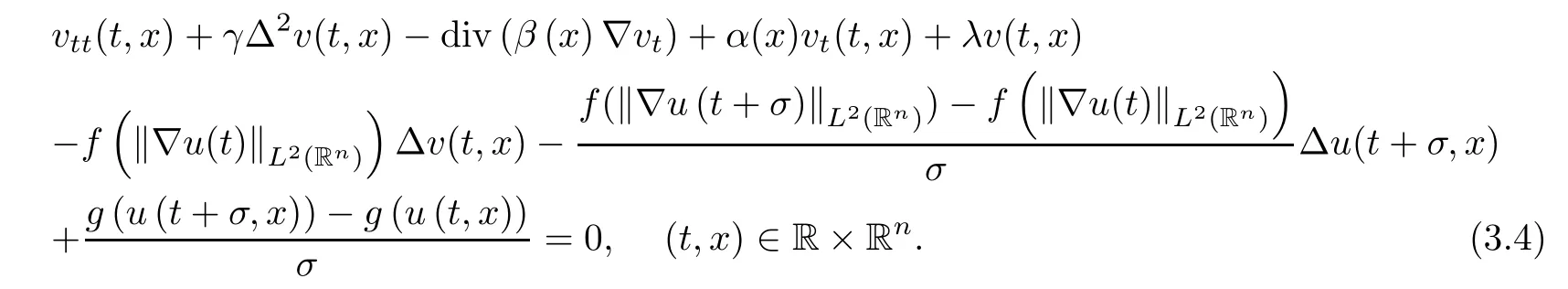
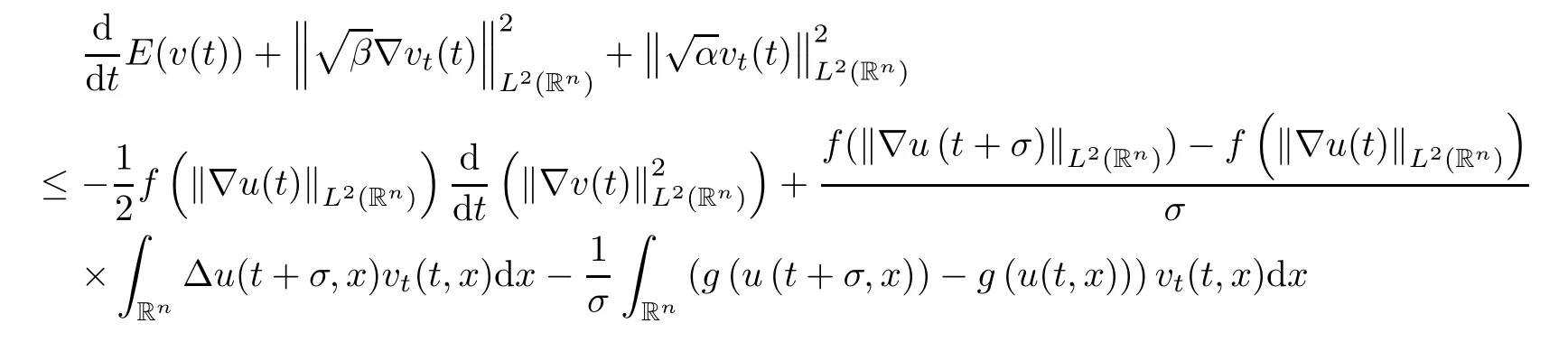

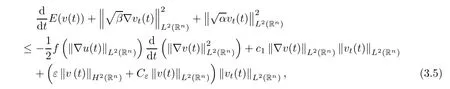
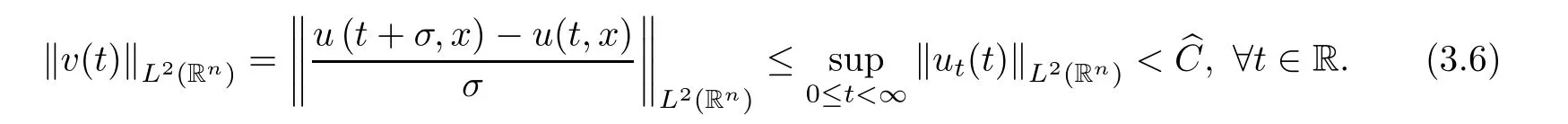

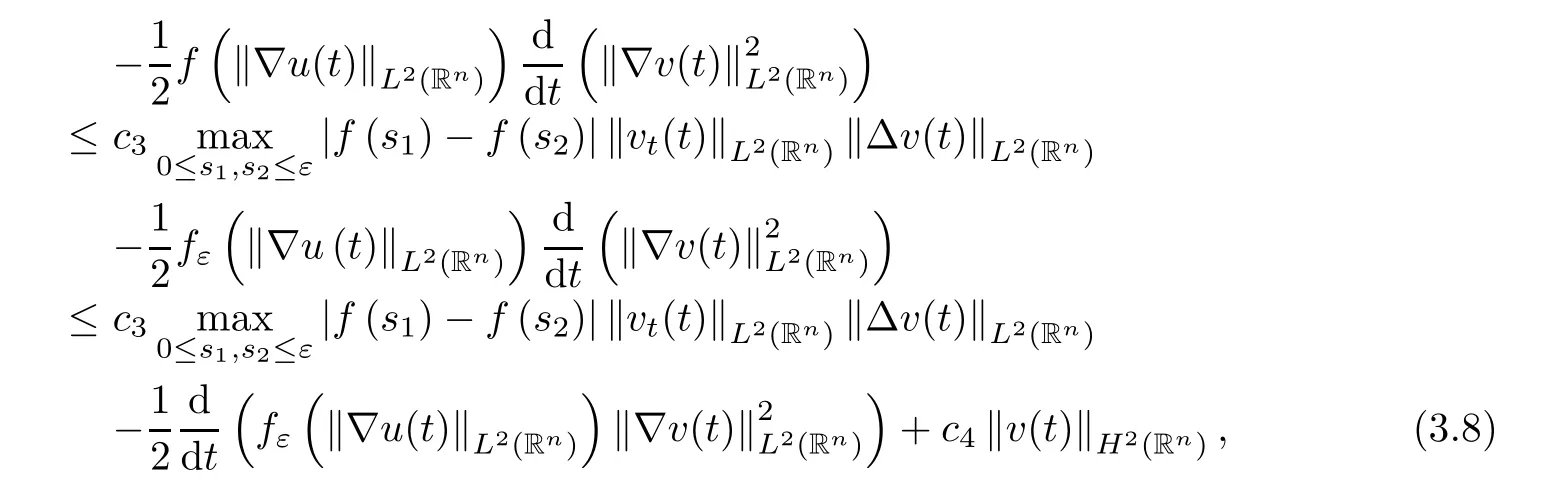

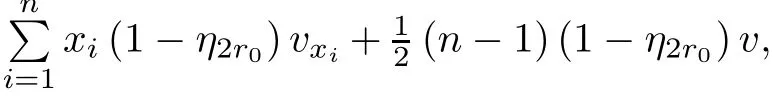
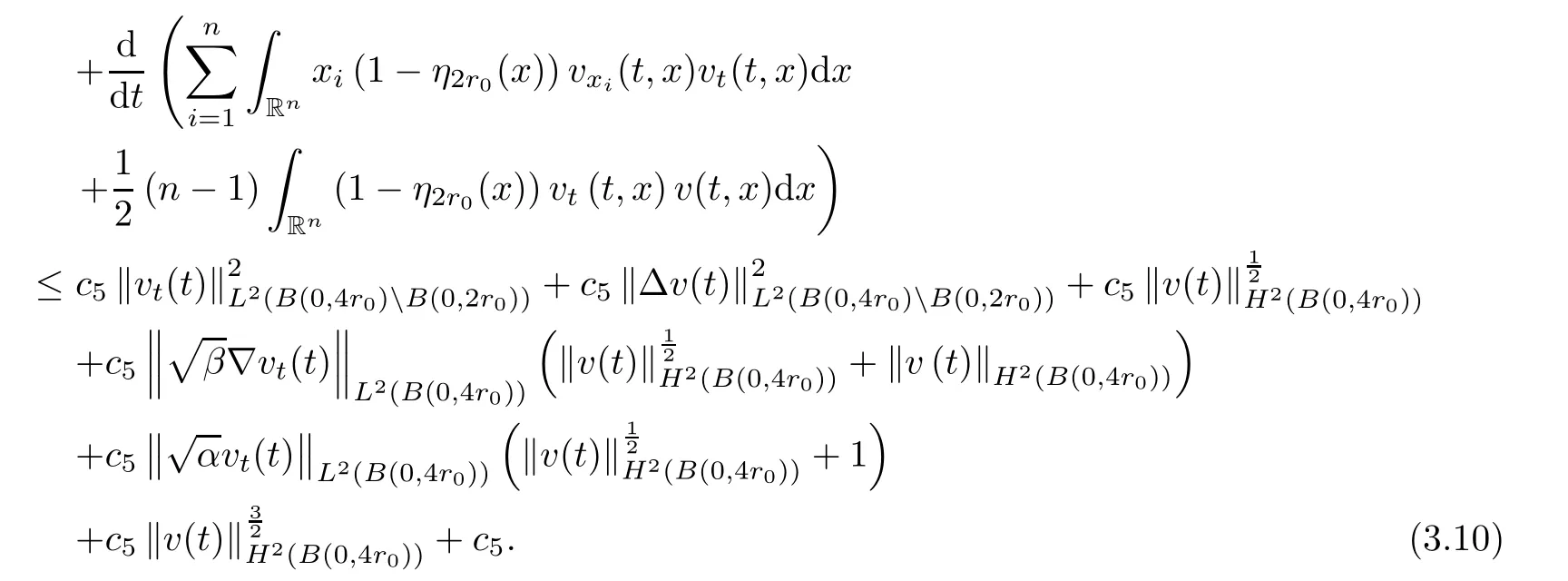
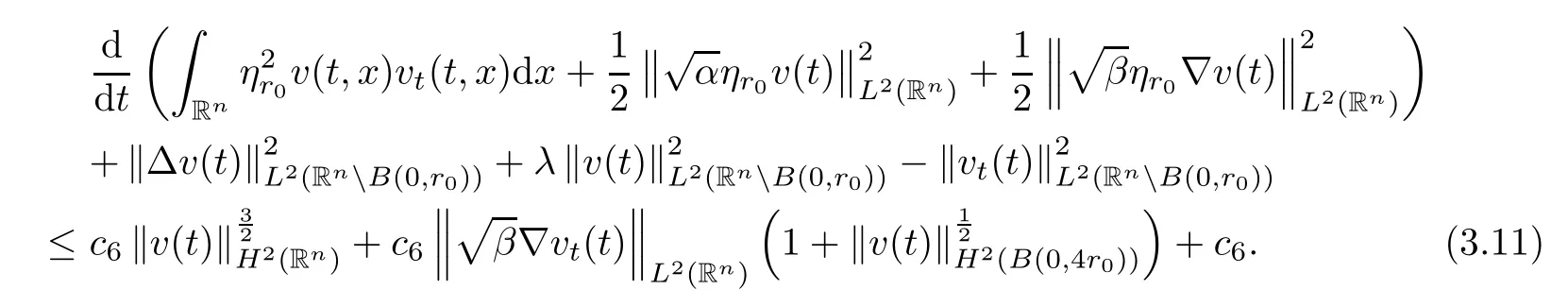
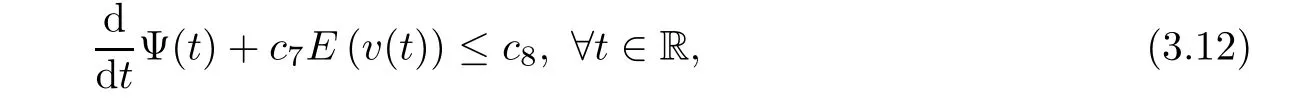
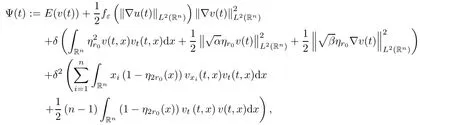

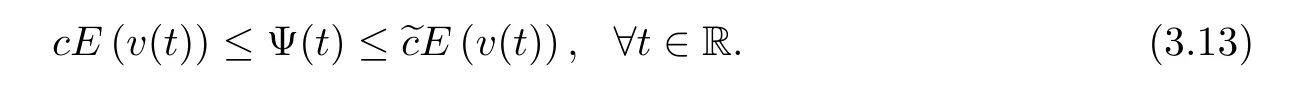

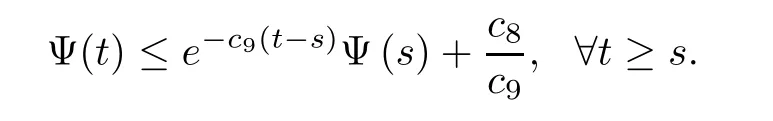
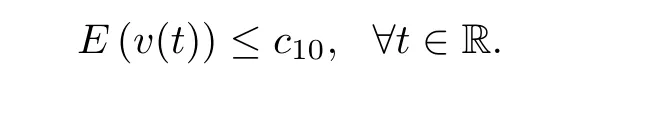


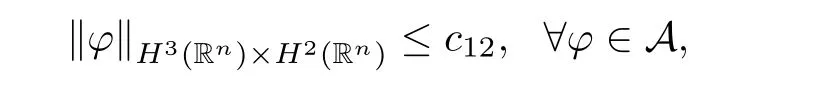
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- HELICAL SYMMETRIC SOLUTION OF 3D NAVIER-STOKES EQUATIONS ARISING FROM GEOMETRIC SHAPE OF THE BOUNDARY∗
- INITIAL BOUNDARY VALUE PROBLEM FOR A NONCONSERVATIVE SYSTEM IN ELASTODYNAMICS∗
- STABILITY OF TRAVELING WAVES IN A POPULATION DYNAMIC MODEL WITH DELAY AND QUIESCENT STAGE∗
- NONLINEAR STABILITY OF VISCOUS SHOCK WAVES FOR ONE-DIMENSIONAL NONISENTROPIC COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH A CLASS OF LARGE INITIAL PERTURBATION∗
- A GENERALIZATION OF GAUSS-KUZMIN-LÉVY THEOREM∗
- THE EVENTUALLY DISTANCE MINIMIZING RAYS IN MODULI SPACES∗
