THE EVENTUALLY DISTANCE MINIMIZING RAYS IN MODULI SPACES∗
2018-07-23FeiSONG宋飞YiQI漆毅GuangmingHU胡光明
Fei SONG(宋飞)Yi QI(漆毅)Guangming HU(胡光明)
LMIB,School of Mathematics and Systems Science,Beihang University,Beijing 100191,China
E-mail:songfei19860810@163.com;yiqi@buaa.edu.cn;18810692738@163.com
Abstract The eventually distance minimizing ray(EDM ray)in moduli spaces of the Riemann surfaces of analytic finite type with 3g+n−3>0 is studied,which was introduced by Farb and Masur[5].The asymptotic distance of EDM rays in a moduli space and the distance of end points of EDM rays in the boundary of the moduli space in the augmented moduli space are discussed in this article.A relation between the asymptotic distance of EDM rays and the distance of their end points is established.It is proved also that the distance of end points of two EDM rays is equal to that of end points of two Strebel rays in the Teichmüller space of a covering Riemann surface which are leftings of some representatives of the EDM rays.Meanwhile,simpler proofs for some known results are given.
Key wordsAugmented Teichmüller space;augmented moduli space;Strebel differential;EDM ray
1 Introduction
Let Xg,pbe a Riemann surface of genus g with p punctures(3g−3+p>0).Denote by Teich(Xg,p)and M(Xg,p)Teichmüller space and moduli space of Xg,p,respectively.
Two holomorphic quadratic differentials q and q′on[Y,f]∈ Teich(Xg,p),or two measured foliations F(q)and F(q′)are called topologically equivalent,if there is a continuous self-mapping ϕ of Y homotopic to the identity mapping,which maps leaves of F(q)to leaves of F(q′)and its restriction to Y − Γqis a homeomorphism of Y − Γqonto Y − Γq′,where Γqand Γq′are the sets of all critical points and critical trajectories of q and q′,respectively.Two holomorphic quadratic differentials q and q′are called similarly equivalent if they are topologically equivalent and the sets of subscripts of non-zero coefficients in the representation of measured foliations

are coincide.Furthermore,if there exists λ>0 such that

where

the quadratic differential q and q′are called modularly equivalent.Here,i(f∗(Gj),V(q))andare intersection numbers ofandwith the measured foliation V(q):=F(−q)and V(q′):=F(−q′),respectively.
It is known that every Teichmüller geodesic ray r starting at some point[Y,f]∈Teich(Xg,p)is induced by some holomorphic quadratic differential q on[Y,f].A ray r is called Strebel if q is a Strebel differential[2].It is proved in[7]that every Strebel ray r has a limit r(∞)on the boundary of Teich(Xg,p)in the augmented Teichmüller spaceDenote bythe Teichmüller distance between the end points r(∞)and r′(∞)of r and r′.
Given two Teichmüller geodesic rays r and r′in Teich(Xg,p),there are three possible situations as follows:They are called bounded if there is M>0 such thatM for any t≥ 0;they are called divergent if the conditionas t→ ∞;and they are called asymptotic if there is a choice of initial points of r and r′such that
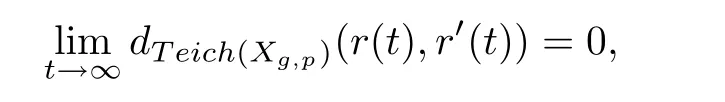
or equivalently,there is a∈R such that

The following theorem is an important result for any two given Strebel rays.
Theorem A([2]) Suppose that r and r′are Strebel rays in Teich(Xg,p)starting at r(0)=[Y,f]and r′(0)=[Y′,f′]with the initial unit norm holomorphic quadratic differentials q and q′on Y and Y′,respectively.Let F(q) ∈ MF(Y)and F(q′)∈ MF(Y′)be the corresponding measured foliations of q and q′,respectively.Ifare similarly equivalent,then

Otherwise,
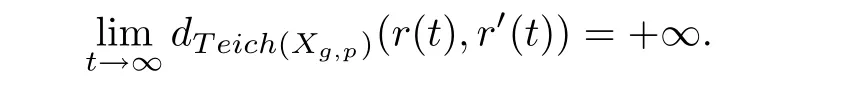
Motivated by Theorem A,we introduce a notion of weakly similar equivalence of measured foliations and obtain the following result about moduli spaces.
Theorem 1.1Suppose that[r]and[r′]are EDM rays in M(Xg,p)starting at[r](0)={Y,f}and[r′](0)={Y′,f′}with the Strebel differentials q and q′on Y and Y′,respectively.Let F(q)∈ MF(Y)and F(q′)∈ MF(Y′)be the corresponding measured foliations of q and q′,respectively.Ifandare weakly similarly equivalent,then
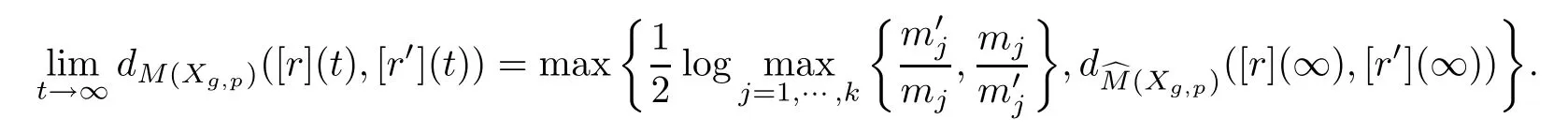
Otherwise,
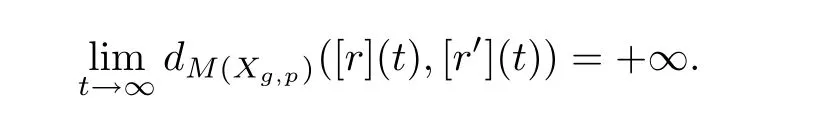
Let Xg=Xg,0.It is known that every holomorphic finitely unramified coveringof a compact Riemann surfaceonto a compact Riemann surface Xgwith genus g≥2 induces an isometric embeddingBecause of Theorem 4.1,we can compare the distance of the end points of two EDM rays in M(Xg)and the end points of two Strebel rays inwhich are the images of representatives of the EDM rays by Φπ.
Theorem 1.2Suppose that[r]and[r′]are EDM rays in M(Xg)starting at[r](0)={R,f}and[r′](0)={R′,f′}with the Strebel differentials q and q′on R and R′,respectively.Let F(q) ∈ MF(R)andbe the corresponding foliations q and q′,respectively.Ifandare weekly modularly equivalent,then there exist two representatives r ∈ [r]and r′∈ [r′]such that
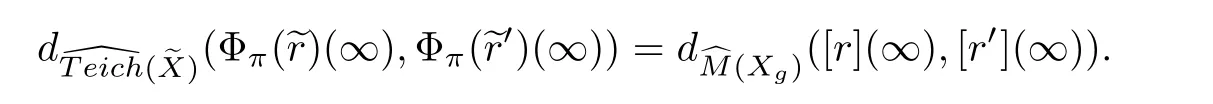
2 Preliminaries
Let Xg,pbe a connected and finite analytic type Riemann surface of genus g with p punctures(3g−3+p>0).A marked Riemann surface modeled on Xg,pis a tuple(Y,f),where Y is a Riemann surface andis a quasiconformal mapping.Two marked Riemann surfaces(Y1,f1)and(Y2,f2)are Teichmüller equivalent if there exists a conformal mapping h:Y1→Y2such that h is homotopic toThe Teichmüller space Teich(Xg,p)can be defined as
Teich(Xg,p)={[Y,f]:(Y,f)is a marked Riemann surface modeled on Xg,p},
where[Y,f]is the Teichmüller equivalence class containing(Y,f).There is a natural complete metricon Teich(Xg,p)called Teichmüller metric,which is defined as
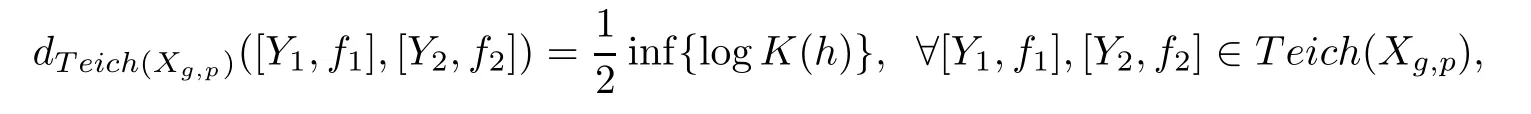
where the in fimum takes over all quasiconformal mappings h:Y1→ Y2homotopic toand K(h)is the maximal dilatation of h(for the details,see[6,12,16]).
The mapping class group Mod(Xg,p)is defined as the group of homotopic equivalent classes of orientation-preserving homeomorphism of Xg,p.Two orientation preserving homeomorphisms φ,ϕ :Xg,p→ Xg,pare equivalent if φ ◦ ϕ−1is isotopic to the identity map on Xg,p.As Mod(Xg,p)acts ondiscontinuously and isometrically,we naturally obtain the quotient space M(Xg,p)as the equivalence classes of Teich(Xg,p)by the action of Mod(Xg,p).Here,denote{Y,f}by a element of M(Xg,p).We call M(Xg,p)the moduli space of Xg,p.And it has the induced metric
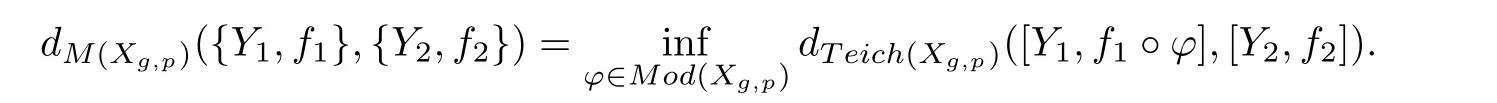
The augmented Teichmüller spaceis composed by all equivalence classes[Y,f]of marked Riemann surfaces and marked noded Riemann surfacesA marked noded Riemann surfacemodeled on Xg,pconsists of a noded Riemann surface[7]and a deformationHere,a deformation is a mapping which contracts some disjoint loops on Xg,pto points(the nodes of)and which is a homeomorphism except these loops.Two marked noded Riemann surfacesandare equivalent if there exists a biholomorphic mappingsuch that h is homotopic toA homeomorphismis called bi-holomorphic if its restriction to every component ofis bi-holomorphic onto a component of
There is a naturally general metricon augmented Teichüller spaceThe distance of two points inmay be∞.It is well-known thatis the partial compactification of the Teichmüller space Teich(Xg,p).The subset ofconsisting of all equivalence classes containing marked noded Riemann surfaces is called the boundary of the augmented Teichmüller spaceWe refer[1,2]for more details on the augmented Teichmüller space.
The orbit space

is called the augmented moduli space of Xg,p.It is proved in[1]that the moduli spacewith the quotient topology is compact.
It is well-known that for two points[Y1,f1]and[Y2,f2]in Teich(Xg,p),there exists an unique geodesic segment which connects[Y1,f1]and[Y2,f2].There is an equivalent description that for a quasiconformal map f:Y1→Y2,there exists an unique Teichmüller mapwhich is homotopic toThe Beltrami differentialµf0can be represented bywhere q is some integrable holomorphic quadratic differential on Y1and 0≤k<1[16].
A holomorphic quadratic differential q[15]on a Riemann surface Xg,pis the form gdz2in every coordinate neighborhood(U,z),where g is a holomorphic function on U.It is called integrable if the normRRis finite.In this article,the quadratic differential is represented as the integrable holomorphic quadratic differential.A smooth path z=γ(t)on Xg,pis a horizontal trajectory of q ifAll horizontal trajectories of q are sorted into three types:critical trajectories,which are horizontal trajectories joining critical points of q;closed trajectories;recurrent trajectories,which are horizontal trajectories dense on the subsurface of Xg,psurrounded by critical trajectories.Here,critical points of a holomorphic quadratic differential q are zeros or first order poles at a puncture of q.A holomorphic quadratic differentialon the surface Xg,pis called Strebel differential,if its non-closed trajectories cover a set of measure zero[13].There exist the special Strebel differentials with only onecylinder[14].
Let(F,µ)be the measured foliation on a compact Riemann surface Xg,p.Here,F is represented as the foliation andµis transverse measure.Denote by S the set of all homotopy classes of non-trivial and non-peripheral simple closed curves on Xg,p.The intersection number of any measured foliation(F,µ)and any α ∈ S is defined as follows:
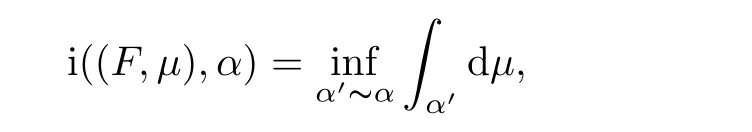
where the in finimum is taken over all simple closed curves α′homotopic to α.Two measured foliations(F1,µ1)and(F2,µ2)are called equivalent if
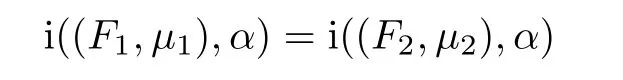
holds for all α ∈ S.Let[F,µ]be the equivalent class of(F,µ)and let MF(Xg,p)be the set of all equivalent classes of measured foliations on Xg,p(for detail,see[6]).
Every quadratic differential q on Xg,phas a natural parameter z=x+iy except finite number of zeros and one order poles.The measured foliation F(q)=(F,µ)of q is the horizontal foliation of q with transverse measureµ=|dx|,where the leaves of F(q)are locally defined by y=constant.It is proved by Hubbard and Masur[8]that every element[F,µ]incontains a measured foliations on Xg,pinduced by an unique quadratic differential q on Xg,p.
For a given holomorphic quadratic differential q on a Riemann surface Xg,p,let Γqbe the set of all critical points and critical trajectories of q.Then,the set Xg,p−Γqare composed by two kinds of domains:annuli which are swept out by closed homotopic trajectories of q,or minimal domains which are made up of ergodic recurrent trajectories of q(for details,see[9]).If q has an annulus A in Xg,p−Γq,the restriction to A of the measured foliation F(q)of q can be represented as F(q)|A=bγ,where γ ∈ S is a simple closed curve,and b>0 is the vertical length of A.If there is a minimal domain M in Xg,p−Γq,the restriction to M of F(q)can be written as F(q)=bβ,where β is an ergodic curve.Therefore,the measured foliation F(q)of q can be written as

where Gjare simple closed curves or ergodic curves which are not homotopic to each other and the intersection number of any two curves is 0,and bi>0 when Giis simple,bi≥0 when Giis ergodic.If a quadratic differential is Strebel if the measured foliation F(q)of q can be written as

where Gjare simple closed curves[13].In[17],the generalised modulus of Gjis given as follows:
where i(Gj,V(q))is the intersection number of Gjwith the measured foliation V(q):=F(−q).
The measured foliations F(q)and F(q′)of quadratic differentials q and q′are called topologically equivalent,if there is a continuous mapping of Xg,ponto Xg,phomotopic to the identity mapping of Xg,psuch that the restriction of ϕ to Xg,p−Γqis a homeomorphism of Xg,p−Γqonto Xg,p−Γq′and maps leaves of F(q)to leaves of F(q′).They are called similarly equivalent if q and q′are topologically equivalent and the sets of subscripts of non-zero coefficients in the representation of measured foliations
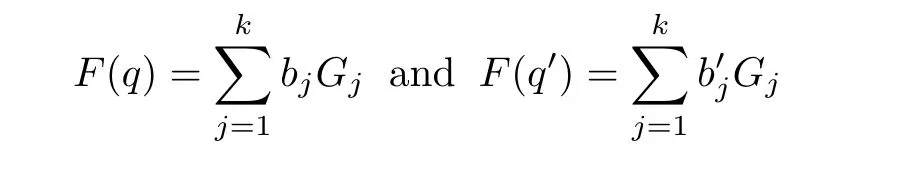
are coincide.
It is clear that every homeomorphism f:Xg,p→Y induces a homeomorphism
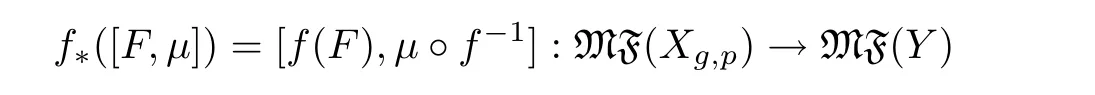
which preserves transverse measures and i(f∗(µ),f∗(ν))=i(µ,ν)for any
Let F(q)and F(q′)be the measured foliations of quadratic differentials q and q′on[Y,f]andrespectively.Ifandare similarly equivalent,then the measured foliations can be represented as

Consequently,
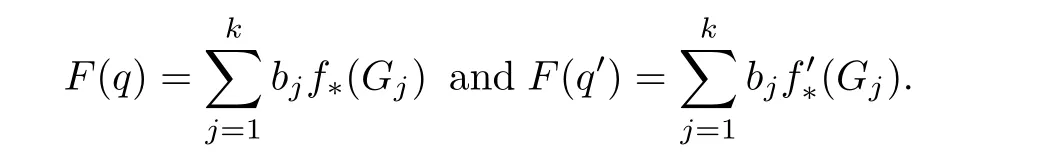
Two quadratic differential q and q′are called modularly equivalent if there exists λ >0 such that

where
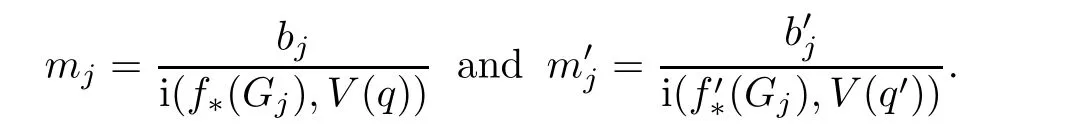
3 Asymptotic Relationship Between Strebel Rays in Teich(X)
The relationships between Strebel rays are important in the study of Teichmüller space.Some notions and known results on the relationships between Strebel rays are recalled,and simple proofs of some known results are also given in this section.
It is clear that a geodesic ray r starting at[Y(t),f(t)]is deduced by the mapping
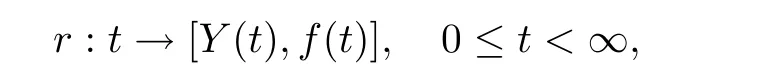
where the Beltrami differentialA ray r is called Strebel if q is a Strebel[3].Two Teichmüller geodesic rays r,r′on Teich(Xg,p)are called bounded if there is M>0 such thatfor any t≥ 0.They are called divergent if the conditionasholds.They are asymptotic[10]in Teich(Xg,p)if there is a choice of basepoints r(0),r′(0)so that

in other words,for the given rays r(t),r′(t),there is a ∈ R such that
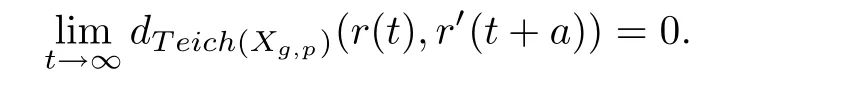
The boundary behavior of Strebel rays on Teichmüller space is also known.Let any Strebel rayin Teich(Xg,p)start at r(0)=[Y,f]with the initial Strebel differential q on Y.It converges to a pointinas t→ ∞ [7].
Let ri(i=1,2)be the Strebel ray in Teich(Xg,p),which starts atwith the initial Strebel differentials qion Yi.If the pull-back measured foliationsandare similarly equivalent,then the measured foliations are written aswhere γjare simple closed curves.There exists a homeomorphismhomotopic to identity.The mappingmaps the core curves f1(γj)to the core curves f2(γj).Set r1(∞)=andLetbe the components ofandsuch thatfor λ=1,···,Λ.The Teichmüller distance between r1(∞)and r2(∞)is defined by

where the in fimum ranges over all quasiconformal mappingssuch that hλis homotopic to.Otherwise,
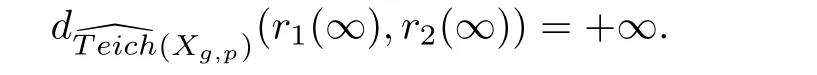
Now,we give some corollaries of Theorem A below,which are of independent meanings.One of them is already known but the proof here is new and the others are new.
Corollary 3.1Let r,r′be the Strebel rays on Teich(Xg,p)starting at r(0)=[Y,f],r′(0)=[Y′,f′]with the initial unit norm holomorphic quadratic differentials q,q′on Y,Y′,respectively.The measured foliationsandare corresponding to q,q′,respectively.Suppose thatare modularly equivalent.Then,there exists b∈R such that the equation
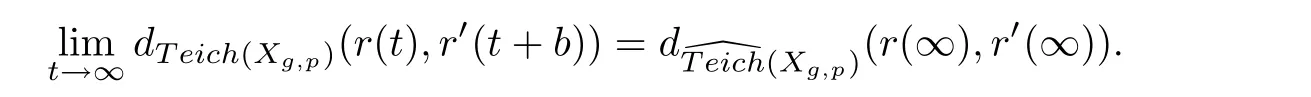
ProofAs the measured foliationsare modularly equivalent,by Theorem A,we obtain the following equation

The module of every cylinder of Strebel differential stretches δ times or shrinks δ times,when the Strebel differential occurs deformation by Teichmüller deformation.Therefore,there exists the quadratic differentials q′(b)at the point r′(b)(b ∈ R)such that λ is equal to 1.Therefore,
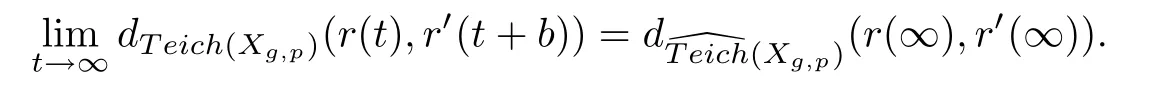
Corollary 3.2([3]) For any two Strebel rays r and r′,they are asymptotic if and only if r,r′are modularly equivalent and r(∞)=r′(∞).
ProofBy definition,it is obvious that r and r′are modularly equivalent and r(∞)=r′(∞)if they are asymptotic.On the other hand,by Corollary 3.1,if r and r′are modularly equivalent,then

Thus,r(∞)=r′(∞)tells us that r and r′are asymptotic. ?
Corollary 3.3For any two one-cylinder Strebel rays r and r′,if they are asymptotic,then r(∞)=r′(∞).Conversely,for a Riemann surfacewith 1 node P,if there exist two one-cylinder Strebel rays r,r′which converge tothey are asymptotic.
ProofIf two one-cylinder Strebel rays r,r′are asymptotic,by Corollary 3.2,then r(∞)=r′(∞).Conversely,for a Riemann surfacewith 1 node P,there exists the one-cylinder Strebel ray r starting at r(0)=[Y,f]which has the initial unit norm Jenkins-Strebel differential q with the same core curve γ homotopic to the puncture P on Y by[5].So,we getwith.If there exists the equation r(∞)=r′(∞),then γ is homotopic to γ′.Because the rays r,r′are modularly equivalent,they are asymptotic. ?
4 Asymptotic Relationship Between EDM Rays in M(Xg,p)
In this section,we discuss the asymptotic relationship between EDM rays in the moduli space M(Xg,p).First,we recall the notion of eventually distance minimizing ray and introduce the definitions of weakly similar equivalence and weakly modular equivalence for quadratic differentials.

Two quadratic differentials q and q′on Y ∈ M(Xg,p)are called weakly similarly equivalent if there is a continuous self mapping ϕ:Y →Y of Y onto itself,which maps leaves of F(q)to leaves of F(q′)and its restriction to Y − Γqis a homeomorphism of Y − Γqonto Y − Γq′,and the measured foliations F(q)and F(q′)of q and q′can be represented as

respectively,where ϕ(Gj)is homotopic tofor j=1,···,k.
Two quadratic differential q and q′on Y ∈ M(Xg,p)are called weakly modularly equivalent if they are weakly similarly equivalent and there exists λ>0 such that

where

Two EDM rays[r]and[r′]in M(Xg,p)are called bounded if there is M>0 such that
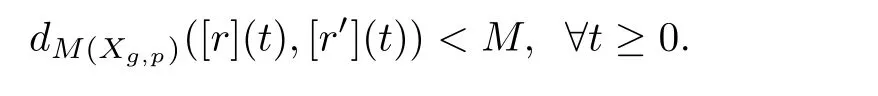
They are called divergent if

They are called asymptotic if there is a choice of basepoints[r](0)and[r′](0)so that

equivalently,there is a∈R such that


Now,we can state one of our main results.
Theorem 4.1Suppose that[r]and[r′]are EDM rays in M(Xg,p)starting at[r](0)={Y,f}and[r′](0)={Y′,f′}with the Strebel differentials q and q′on Y and Y′,respectively.Letandbe the corresponding measured foliations of q and q′,respectively.Ifandare weakly similarly equivalent,then
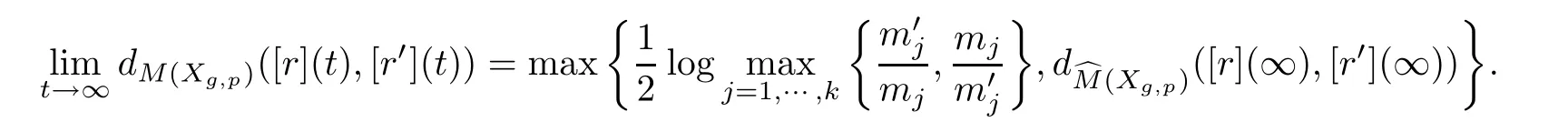
Otherwise,
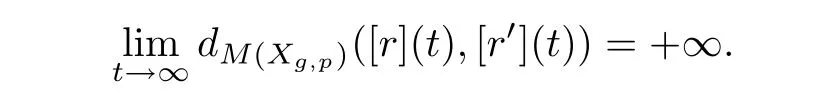
ProofIfandare weakly similarly equivalent,then there is a continuous mapping ϕ of Xg,ponto itself,which maps leaves ofto leaves ofand its restrictionis a homeomorphism,such thatandcan be represented as

where ϕ(Gj)is homotopic to,for j=1,···,k.
The mapping ϕ can be decomposed by a representational element ψ ∈ Mod(Xg,p)and a continuous mapping φ of Xg,ponto Xg,psatisfied with ϕ = φ ◦ ψ,where ψ(Gj)is homotopic tofor j=1,···,k and φ is homotopic to the identity mapping.As the modular group is discrete,there is a uniform bound of the order of any group stabilizing any point of Teich(Xg,p).Therefore,there are finite Strebel rays r in the equivalent class of[r].
Let r1be a representative element of a EDM ray[r]in M(Xg,p).For any representative r2of the EDM ray[r],there exists a element[η]∈ Mod(Xg,p)such that a representative element η of[η]makes η∗◦r1(t)=r2(t)for all t≥ t1,where t1is sufficient lager positive number.If[r]and[r′]are weakly similarly equivalent,we can choose two representative elements r1andof[r]and[r′],respectively.There are two conditions when we choose the representative elements r1andIn the first case,r1andare not similarly equivalent,then
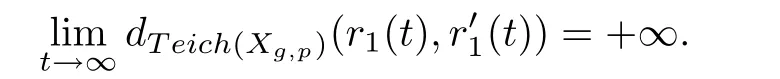
In the second case,r1andare similarly equivalent,andis finite.It is easy to be obtained that the limit metric of the second case is the minimal,therefore,

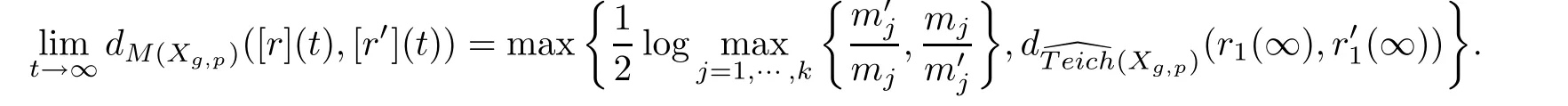
As
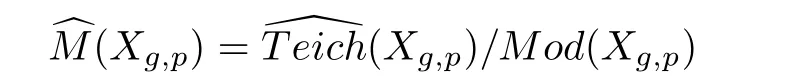

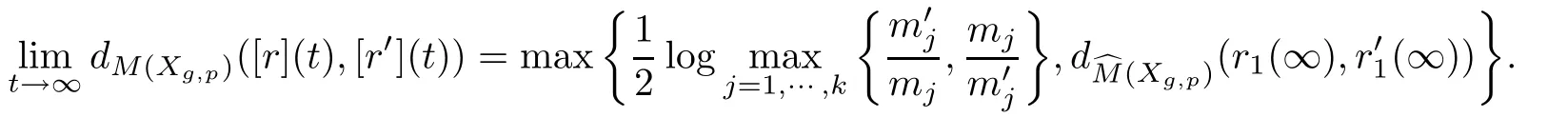
On the other hand,for any two representations r1andof[r]and[r′]are not similarly equivalent in Teich(Xg,p),the equation
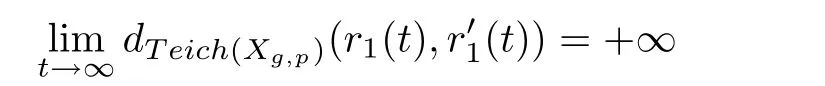
holds.By the definition of the metric of M(Xg,p),we obtain

By Theorem 4.1,we deduce the following corollary 4.2,which can derive a result of Farb and Masur[5]easily.
Corollary 4.2Suppose that[r]and[r′]are EDM rays in M(Xg,p)starting at[r](0)={Y,f}and[r′](0)={Y′,f′}with the Strebel differentials q and q′on Y and Y′,respectively.Letandbe the corresponding measured foliations of q and q′.Ifandare weakly modularly equivalent,then there exists b∈R such that

ProofIfare modularly equivalent in M(Xg,p),then by Theorem 4.1,we have

By the definition of modular equivalence,we haveAs t varies continuously when the rays go closer to the boundary of moduli space M(Xg,p).We can choose b∈R such that the EDM ray r′in bλ =1 holds for each cylinder.Therefore,we obtain
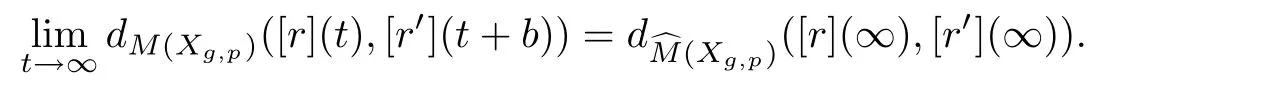
Corollary 4.3([5]) For any two EDM rays[r],[r′],they are asymptotic if and only if[r],[r′]are weakly modularly equivalent and[r](∞)=[r′](∞).
ProofIf they are asymptotic,by the definition,it is obvious that r and r′are modularly equivalent and r(∞)=r′(∞).On the other hand,by Corollary 4.2,if r and r′are modularly equivalent,there exists b∈R such that

And it is easy to be get that r and r′are asymptotic by r(∞)=r′(∞).
5 The Relation of the Distance Between End Points of EDM Rays in M(Xg,0)and End Points of Strebel Rays in
Suppose that Xg=X(g,0)is a compact Riemann surface with genus g>2.Letbe a compact Riemann surface which is the finitely unramified covering surface of X(g,0)with holomorphic covering mappingFor every marked Riemann surface(Y,f)of Xg,there is marked Riemann surfacesuch that the following diagram

are commutative.So,we can define a mappingof the space of marked Riemann surfaces of Xginto that ofby sending(Y,f)to,which induces a mapping
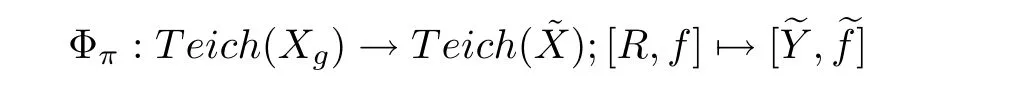
naturally.
By the lifting theorem of maps,we have the following Lemma 5.1,which is parallel to that by Kra in terms of fundamental groups of Riemann surfaces.
Lemma 5.1([11]) If the mappingis the finitely unramified holomorphic covering mapping as above,then π can induce a naturally isometric embedding Φπ:Teich(Xg) →
ProofAs Xgis a compact Riemann surface,the covering transformation group G of the upper half-plane H over Xgis finitely generated Fuchsian group and is of the first kind.The mappingis the finitely unramified covering,therefore the covering transformation groupof the upper half-plane H overis a finite index subgroup of G.From[11],we know there exists a naturally isometric embedding?
Now,we prove that the images of Strebel rays in Teichmüller space Teich(Xg)under isometric embedding Φπare Strebel rays inPrecisely,we prove that the lifts of Strebel differentials in Teich(Xg)are still Strebel differentials in.This is the following Lemma 5.2.
Lemma 5.2A holomorphic quadratic differentialon the surface Y is Strebel differential if and only if the lifting differentialof q on the surfaceis Strebel differential.
ProofIt is well known that the trajectory of holomorphic quadratic differential is closed or dense. Suppose that q is a strebel differential on the compact Riemann surface Y ∈Teich(Xg).We consider the case that α :[0,1] → Y satisfied with α(0)= α(1)=p0is a closed trajectory of q.For an arbitrary lifting pointofis the lifting curve of α with the initial pointandis another lifting point of p0.The curveis a lift of α with the initial point.As the covering degree is finite,the curve must go back toafter finite times and is the simple closed curve.We can see that the pre-image set of α are the combination of disjoint and closed curves.So,the pre-image set of the closed trajectories of holomorphic quadratic differential q are closed trajectories onFrom the definition of Strebel differential,we know its non-closed trajectories cover a set of measure zero.The pre-image set of the set of non-closed trajectories of q are finite superposition of the set of non-closed trajectories of q.So,the measure of the set of non-closed trajectories ofis zero.We prove that the lift of the Strebel differential q is Strebel differential.
Then,we obtain the connection of the similar equivalence between the quadratic differentials on the bottom surface and the quadratic differentials on the lifting surface as follows:
Lemma 5.3Let q and q′be two holomorphic quadratic differentials on Y and Y′,respectively.If the pull-back measured foliationsandare similar equivalence and they are represented asthen for the holomorphic mappingthe measure foliations of the lifting quadratic differentialsandandare similar equivalence and their pull-back measured foliations can be written asAnd we setandfor j=1,···,k and i=1,···,nj.Then,it follows thatandi=1,···,nj.

The following result tells that the quality of modular equivalence remains unchanged with the process of lifting:
Corollary 5.4The measured foliations of two holomorphic quadratic differentials q on Y and q′on Y′are modularly equivalent.Then,the lifting quadratic differentialsonandonare modularly equivalent.
ProofIf the measured foliations of q,q′are modularly equivalent,so there exists λ >0 such thatfor any j=1,···,k by the proof of Lemma 5.3.It is also easy to knowfor any i=1,···,nj,j=1,···,k.So,the quadratic differentialsare modularly equivalent by the proof of Lemma 5.3. ?
Here,denote by Mπ(Xg)the quotient spaceBy Lemma 5.1,the spaces Teich(Xg)and Φπ(Teich(Xg))are isometric isomorphism.And the following lemma gives the relationship betweenand Mod(Xg).Denote by πg(Xg,x0)andthe fundamental groups of Xgandfixed the initial points.As there exist some elements in the modular group Mod(Xg)which can not be lifted ontobe the elements in the subgroup of[4],the EDM rays in M(Xg)may not be embedded in Mπ(Xg).However,we have the following lemma.
Lemma 5.5([4]) If the mappingis a finite-sheeted,un-branched covering.For any homeomorphism f:Xg→Xg,there exists k≥1 such that fkhas a lift on
Thanks to Lemma 5.5,we obtain the following result.
Lemma 5.6For any element[f]∈Mod(Xg),there exists k≥1 such thatis an elementwhereis a lift of fk.
ProofIt is easy to get the result by Lemma 5.5.The detail of the proof is omitted. ?
Corollary 5.7For any two representational Strebel rays r1,r2of[r]∈M(Xg)(We say two Strebel rays are equivalent if there is a element[η] ∈ Mod(Xg)and t1>0 such that[η]∗◦ r1(t)=r2(t)holds for all t ≥ t1),there exists k ≥ 1 such that the raysand Φπ(r2)are equivalent,that is,they are two representational Strebel rays of an element in Mπ(Xg).
ProofFor any two representational Strebel raysthere is a element[η]∈ Mod(Xg)and t1>0 such thatholds for all t ≥ t1.As there exists k≥1 such thatis an elementLemma 5.6,using the commutative diagram as follows:

we get

Next,we can compare the distance between the end points of of two EDM rays in M(Xg)and the end points of two Strebel rays in Teich(eX)as follows.
Theorem 5.8Let[r],[r′]be EDM rays in M(Xg)starting at[r](0)={R,f},[r′](0)={R′,f′}with the Strebel differentials q and q′on R and R′,respectively.The measured foliationsare corresponding to q,q′,respectively.Ifare weakly modularly equivalent in M(Xg,0),there exist two representational elements r and r′such that the rays Φπ(r)and Φπ(r′)satisfy with the equation

ProofThe measured foliationsare weakly modularly equivalent in M(Xg),therefore,according to Corollary 4.2,there exists b∈R such that the equation
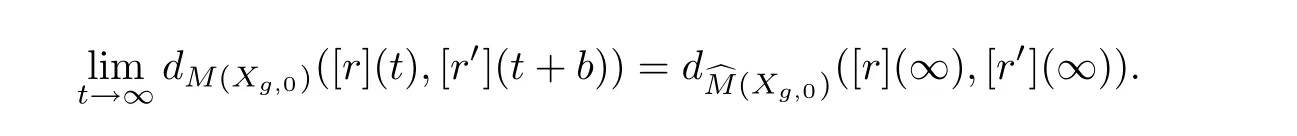
From the proof of Theorem 4.1,there exist two representational elements r and r′of[r]and[r′]such that
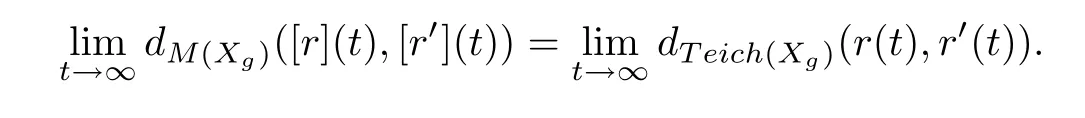
Therefore,the equation

holds.According to Lemma 5.1,we get the equation

As the measured foliations of r and r′are modularly equivalent in Teich(Xg),according to Corollary 5.4,the measured foliations ofandinducing the raysandare modularly equivalent in.From Corollary 3.1,it holds that

Therefore,

Corollary 5.9For a representational elementwith one node,suppose that there exist two one-cylinder Strebel EDM rays[r],[r′]converging toThen,there exist two representational elements r and r′such that the Strebel rays Φπ(r)and Φπ(r′)satisfy with
ProofAs[r],[r′]converge tothe EDM rays[r](∞)=[r′](∞).As two one-cylinder Strebel EDM rays[r],[r′]converge to˙Y,they are weakly modularly equivalent in M(Xg,0).Therefore,they are asymptotic.According to Theorem 5.8,there exist two representational elements r and r′such that the Strebel rays Φπ(r)and Φπ(r′)satisfy with the equation

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- HELICAL SYMMETRIC SOLUTION OF 3D NAVIER-STOKES EQUATIONS ARISING FROM GEOMETRIC SHAPE OF THE BOUNDARY∗
- INITIAL BOUNDARY VALUE PROBLEM FOR A NONCONSERVATIVE SYSTEM IN ELASTODYNAMICS∗
- LONG-TIME DYNAMICS OF THE STRONGLY DAMPED SEMILINEAR PLATE EQUATION IN RN∗
- STABILITY OF TRAVELING WAVES IN A POPULATION DYNAMIC MODEL WITH DELAY AND QUIESCENT STAGE∗
- NONLINEAR STABILITY OF VISCOUS SHOCK WAVES FOR ONE-DIMENSIONAL NONISENTROPIC COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH A CLASS OF LARGE INITIAL PERTURBATION∗
- A GENERALIZATION OF GAUSS-KUZMIN-LÉVY THEOREM∗
