A BOUNDARY SCHWARZ LEMMA FOR PLURIHARMONIC MAPPINGS FROM THE UNIT POLYDISK TO THE UNIT BALL∗
2018-07-23LingLI李灵HongyiLI李红裔DiZHAO赵迪
Ling LI(李灵)Hongyi LI(李红裔)Di ZHAO(赵迪)
LMIB,School of Mathematics and Systems Science,Beihang University,Beijing 100191,China
E-mail:normalee 2013@163.com;hylbuaa@163.com;zdhyl2010@163.com
Abstract In this article,we present a Schwarz lemma at the boundary for pluriharmonic mappings from the unit polydisk to the unit ball,which generalizes classical Schwarz lemma for bounded harmonic functions to higher dimensions.It is proved that if the pluriharmonic mapping f∈P(Dn,BN)is C1+αat z0∈Er⊂∂Dnwith f(0)=0 and f(z0)=w0∈∂BN for any n,N ≥ 1,then there exist a nonnegative vector λf=(λ1,0,···,λr,0,···,0)T ∈ R2n satisfyingfor 1≤ i≤ r such that whereand are real versions of z0and w0,respectively.
Key words Boundary Schwarz lemma;pluriharmonic mapping;unit polydisk;unit ball
1 Introduction
As one of the most famous results in complex analysis,the Schwarz lemma[1–10]has drawn much attention in recent years,especially in several complex analyses.Some commonly known results,such as Schwarz lemmas for holomorphic mappings corresponding to the unit ball and polydisk[1,2,13,14],the boundary Schwarz lemma for holomorphic mappings between unit balls[3],and the Schwarz-Pick type estimates of pluriharmonic mappings in the unit polydisk[4],play important roles in the field of Schwarz lemma research.For example,as an indirect extension of results in[1],authors in[5]presented a Schwarz-Pick lemma for the modulus of holomorphic mappings between p-balls.With the popularity of Schwarz lemma,furthermore,some extended results associated with boundary Schwarz lemma have also been presented based on different mappings and domains,such as pluriharmonic mappings between unit balls[6],and Schwarz lemma at the boundary of strongly pseudoconvex domain in Cn[7].Theories on strongly pseudoconvex are also hot topics discussed like Schwarz lemma.Specially in[11,12],discussions about peak function are really similar to the results of boundary Schwarz lemma.However,so far as we know,there is no discussions about boundary Schwarz lemma presented for the pluriharmonic mappings from the polydisk to the unit ball,and that is the most direct reason for us to write this article.

And Cα(V)represents the set of all functions f on a bounded domain V ∈Cnfor which

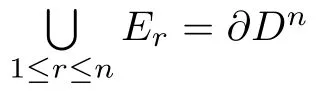
Classical Schwarz lemma[1]states that for every holomorphic mapping of D into itself satisfying the condition f(0)=0,it holds that

which implies

holds for every holomorphic mapping g of D into itself.In[2],the result of boundary Schwarz lemma for holomorphic mappings on D is described as follows.
Theorem 1.1([8]) Let f be the self-holomorphic mapping of D.If f is holomorphic at z=1 with f(0)=0 and f(1)=1,then f′(1)≥ 1.
Specially,Liu et al[2]presented the result of Schwarz lemma for holomorphic mappings from the unit polydisk Dnto the unit ball BNat the boundary,which is described in the following theorem.
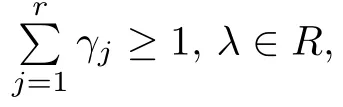

For the harmonic mappings of D into itself,there are also some interesting results closely related to Schwarz lemma.
Theorem 1.3([6]) If f is a harmonic mapping of D into itself,and f(0)=0,then
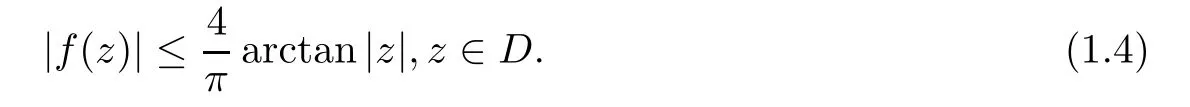
Theorem 1.4([6]) If f is a harmonic mapping of D into itself,then

Apparently,Theorem 1.4 is a generalized version of Theorem 1.3,where the condition f(0)=0 is removed.
In[4],Chen et al presented the Schwarz-Pick type estimates of arbitrary order partial derivatives for bounded pluriharmonic mappings defined in the unit polydisk.
Theorem 1.5([4])Let f∈P(Dn,D),then

where α =(α1,···,αn)is a multi-index with αj>0,j ∈ {1,···,n}.
Theorem 1.6([4]) Let f∈P(Dn,BN)for n,N≥1,then

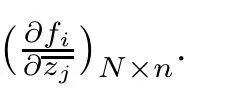
Specially,if we add the condition that f(0)=0,then

When n=N=1,(1.8)is equivalent to(1.4).
Inspired by[2,4,6],but mainly by[2],we consider the boundary Schwarz lemma for pluriharmonic mappings from the unit polydisk to the unit ball in this work.
As Dnand BNare equivalent to the unit polydisk D2n⊂R2nand the unit ball B2N⊂R2N,respectively,we consider the real version of this problem.For z=(z1,···,zn)T∈ Cnwith zj=xj+iyjfor 1 ≤ j ≤ n,denote z′=(x1,y1,···,xn,yn)T∈ R2nas the real version of z.
Referring to[3],where Liu et al presented the boundary Schwarz lemma for holomorphic mappings between unit balls of different dimensions,and by Theorem 1.6,we get the following boundary Schwarz lemma for pluriharmonic mappings in P(Dn,BN).
Theorem 1.7Let f∈P(Dn,BN)with f(0)=0 for n,N≥1.For a given z0∈∂Dn,assume z0∈Erwith the first r components at the boundary of D for some 1≤r≤n.If f is C1+αat z0and f(z0)=w0∈ ∂BN,then there exist a nonnegative vector λf=(λ1,0,···,λr,0,···,0)satisfyingfor 1≤ i≤ r such that
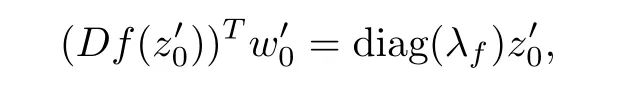
2 Proof of Theorem 1.7
The following lemma plays a significant role in the proof of our main result.
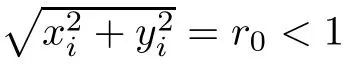
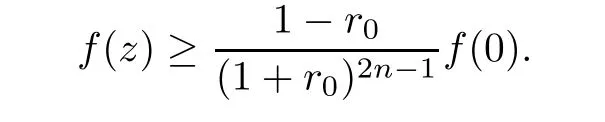
ProofAccording to the description of Theorem 3.1 in[6],it holds that for a nonnegative function f defined on the unit ball B2nin R2n,if f is continuous on the ball and harmonic on its interior,then for any point z′=(x1,y1,···,xn,yn)Twith|z′|=r0<1,we have


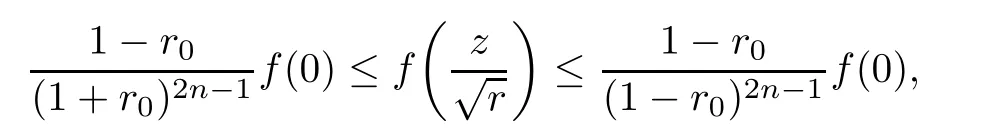
from which we have
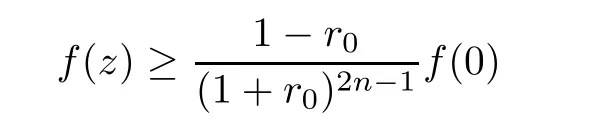
when applying the maximum modulus principle.
In the following,we will prove Theorem 1.7 by the following five steps.
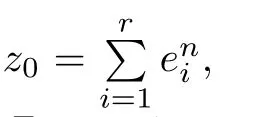

which gives that

Letting xi→1−and referring to[2],we can derive
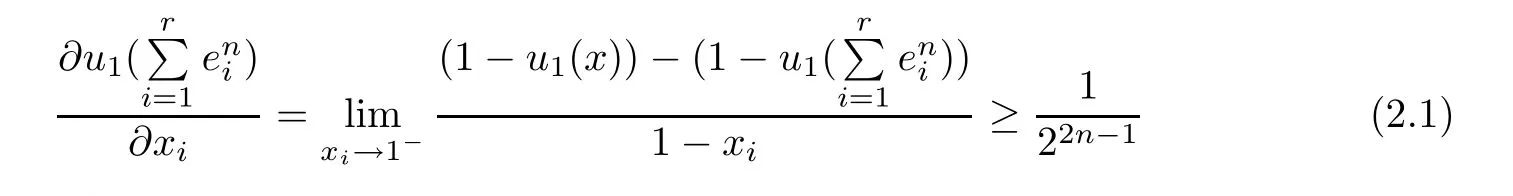
for 1≤i≤r(r≤n).

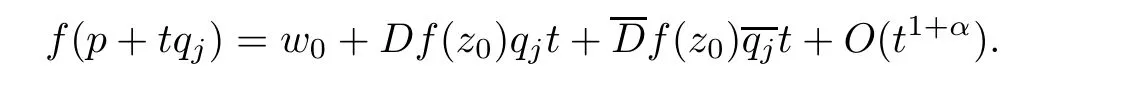
By the special case of Theorem 1.6,when f(0)=0,
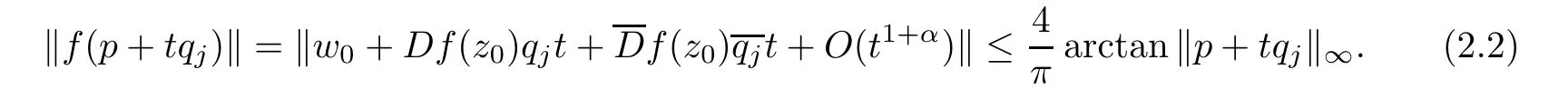
Considering that
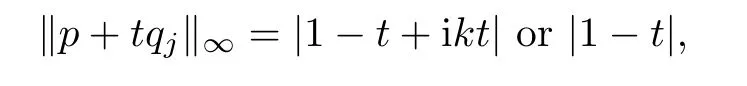
and it is not difficult to derive
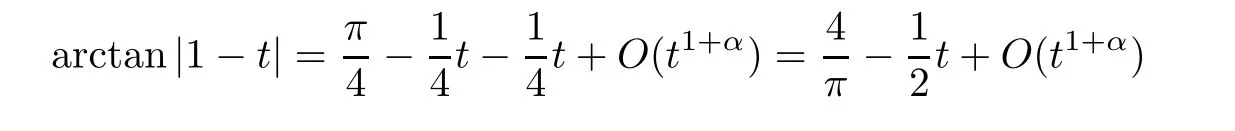
and

when referring to[6].Thus,(2.2)is equivalent to
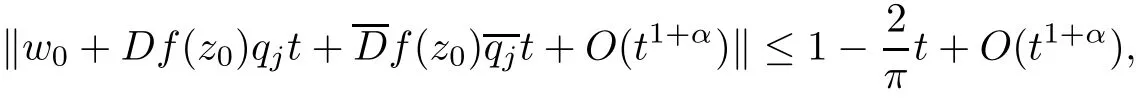
which means that

Letting t→0+,we have


that is,

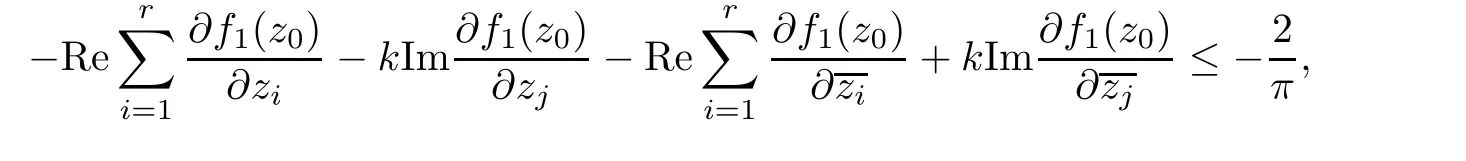
that is,

As(2.4)is valid for any k∈R,it holds that

which gives

and

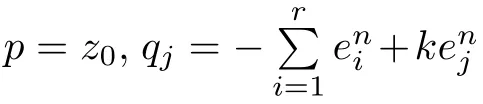

Same as Step 2,it is not difficult to obtain
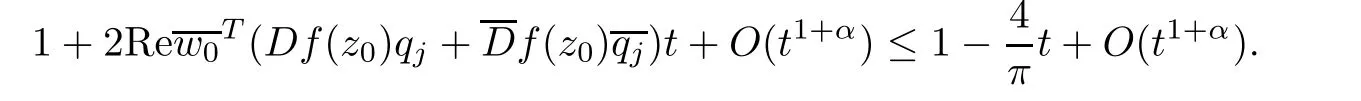
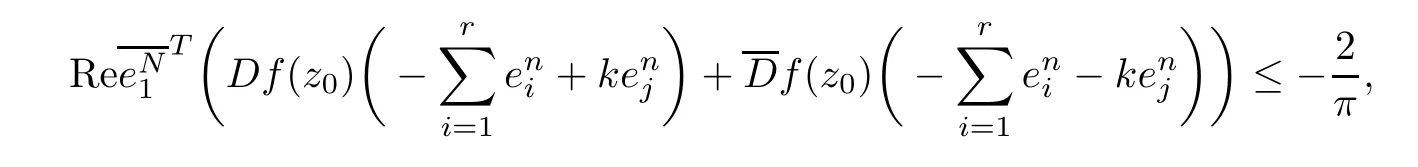
that is,
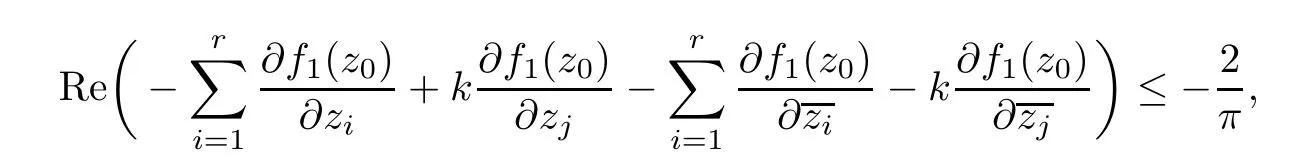
which is equivalent to
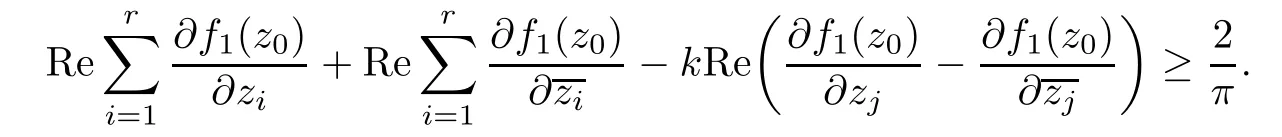
As(2.6)and(2.7)is valid for k∈R,

holds for k≤0 and 1≤j≤r.Thus,we can derive

because k≤0 is arbitrary.


from which it is obvious that
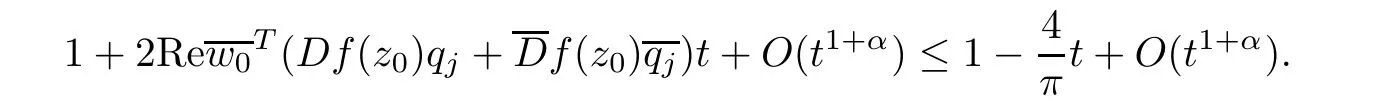

that is,

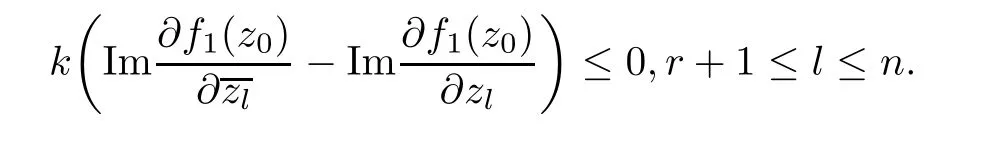
As the above equality is valid forwe have
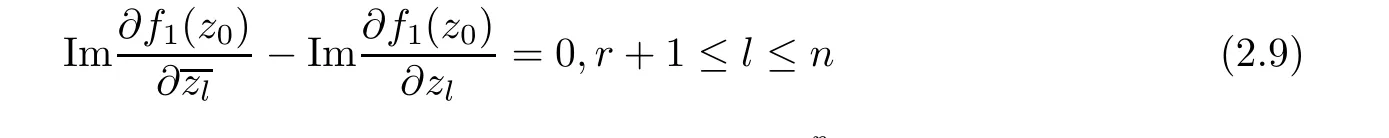
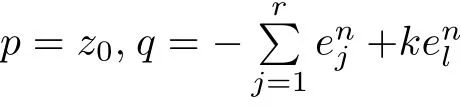
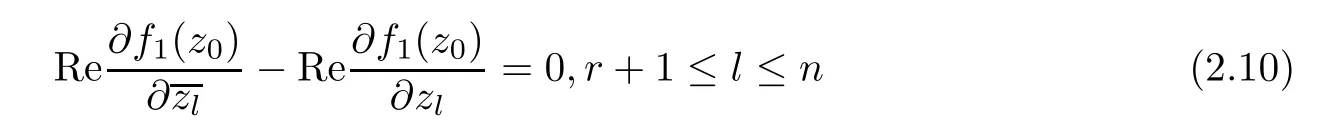
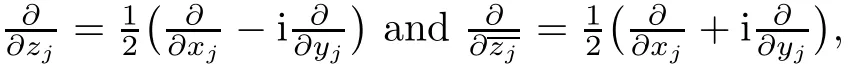

According to(2.1)and(2.5),it is obvious that
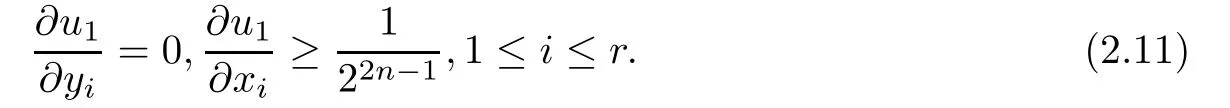
Similarly,according to(2.9)and(2.10),we have
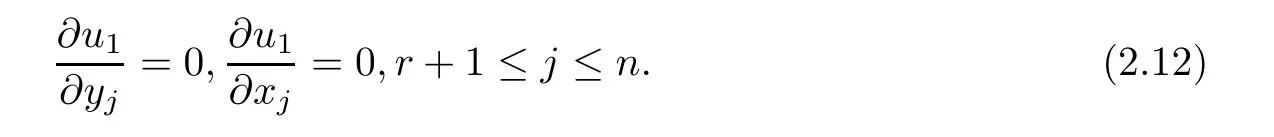

Step 5Letbe any given point atwith the first r pairs of components at the boundary of D2⊂R2,that is,is not necessary,then,there exists a special kind of real-valued diagonal unitary matrix Uz0′such thatwhen referring to[2].Assume that f′is the real version of f,andwhereis not necessaryat∂B2N.Then,there exists a Uw0′such that.Denote
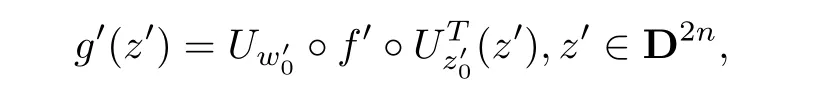
and
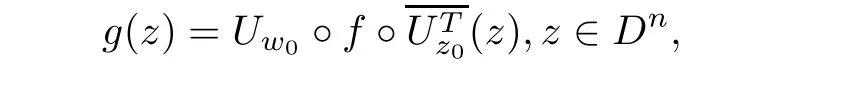
where Uw0and Uz0represent complex unitary matrices corresponding to Uw0′and Uz0′,respectively,such that andThen,we can draw the conclusion that g′is the real version of g andFurthermore,the Jacobian matrix of g could be denoted as
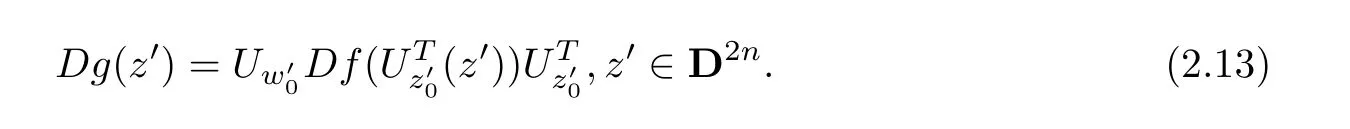
According to Step 4,it is not difficult to obtain


that is,
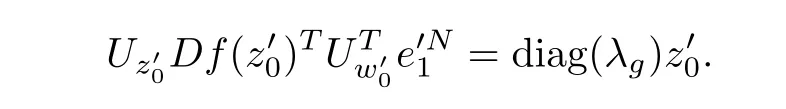
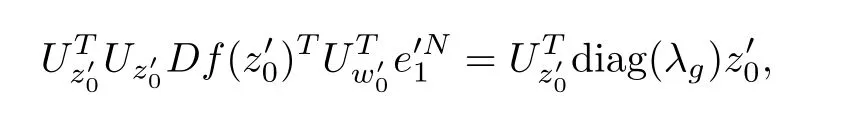
that is,
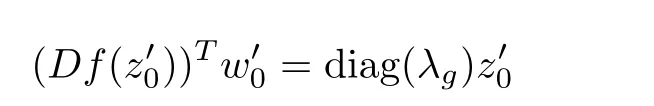
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL EXISTENCE OF CLASSICAL SOLUTIONS TO THE HYPERBOLIC GEOMETRY FLOW WITH TIME-DEPENDENT DISSIPATION∗
- NONNEGATIVITY OF SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL-ALGEBRAIC EQUATIONS∗
- GROWTH AND DISTORTION THEOREMS FOR ALMOST STARLIKE MAPPINGS OFCOMPLEX ORDER λ∗
- EXACT SOLUTIONS FOR THE CAUCHY PROBLEM TO THE 3D SPHERICALLY SYMMETRIC INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
- PRODUCTS OF RESOLVENTS AND MULTIVALUED HYBRID MAPPINGS IN CAT(0)SPACES∗
- CONVERGENCE FROM AN ELECTROMAGNETIC FLUID SYSTEM TO THE FULL COMPRESSIBLE MHD EQUATIONS∗
