GROWTH AND DISTORTION THEOREMS FOR ALMOST STARLIKE MAPPINGS OFCOMPLEX ORDER λ∗
2018-07-23XiaofeiZHANG张晓飞
Xiaofei ZHANG(张晓飞)
School of Mathematics and Statistics,Pingdingshan University,Pingdingshan 467000,China
E-mail:zhxfei@mail.ustc.edu.cn
Jin LU(卢金)†
Department of Mathematics,Huzhou University,Zhejiang 313000,China
E-mail:luking@zjhu.edu.cn
Xiaofei LI(李晓非)
School of Mathematics and Statistics,Pingdingshan University,Pingdingshan 467000,China
E-mail:lixiaofeide9999@163.com
Abstract In this article,the sharp growth theorem for almost starlike mappings of complex order λ is given firstly.Secondly,distortion theorem along a unit direction is also established as the application of the growth theorem.In particular,using our results can reduce to some well-known results.
Key words Distortion theorem;convex mapping;Schwarz lemma at the boundary
1 Introduction
Let C be the complex plane andThe unit disk in C is denoted by D.Let Cnbe the space of n complex variables z=(z1,···,zn)′with the Euclidean inner productand the Euclidean normwhere z,w∈Cnand the symbol′means transpose.The unit ball Bn={z∈ Cn:kzk<1}.Let X be a finite dimensional complex Banach space with norm k.k,B={x∈X:kxk<1}be the unit ball in X,and X∗be the dual space of X.Suppose thatis a domain.Let H(Ω)be the set of all holomorphic mappings from Ω into X.A holomorphic mapping f:Ω → X is said to be biholomorphic if the inverse f−1exists and it is holomorphic on the open set f(Ω).A mapping f ∈ H(Ω)is said to be normalized if f(0)=0 andDf(0)=I,where Df(0)is the Fréchet derivative of f at the origin and I is the identity operator on X.A mapping f ∈ H(Ω)is called locally biholomorphic if Df(x)is nonsingular at each x∈Ω.For each x∈X�,we define T(x)={Tx∈X∗:kTxk≤1,kTx(x)k=kxk}.By the Hahn-Banach theorem,T(x)is nonempty.For any fixedbecauseandwe getIn particular,Trx=Txwhen r>0.
Recall the class M given by

which is related in higher dimensions to the Carathéodory class of functions with positive real part in the unit disk D.
In the case of one complex variable,the following classical growth and distortion theorem is well known.
Theorem A([1]) If f is a biholomorphic function on the unit disk D={ζ∈ C:|ζ|<1}with f(0)=0 and f′(0)=1,then
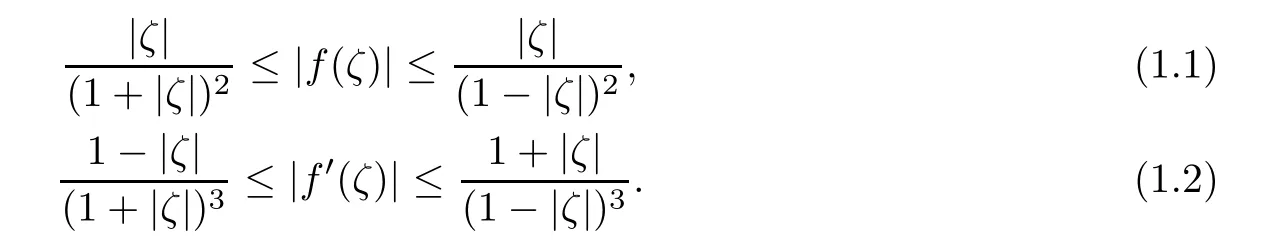
In 1933,H.Cartan[2]maybe firstly raised the ideas that generalize the geometric function theory on complex plane C to several complex variables.However,he found that the results for one complex variable were not true in the case of several complex variables if there was not other restrictive condition,and he gave the following example,

Obviously,f is a biholomorphic mapping,and f(0)=0 and Df(0)=I.But the norm kf(z)k can not be controlled as in inequalitis(1.1).And detDf(z)and Df(z)f(z),for the holomorphic mapping f,have no finite upper bound and no non-zero lower bound as in inequalitis(1.2).At the same time,he suggested to study the property of biholomorphic starlike mappings and biholomorphic convex mappings.Until 1989,Barnard et al[3] firstly established the growth and 1/4-covering theorems for normalized biholomorphic starlike mappings on the unit ball Bn,which extend the corresponding result(1.1)in Theorem A.After that,for the class of normalized biholomorphic starlike mappings and the subclass of starlike mappings,several authors,Gong et al[4],Pfaltzra ff[5],Zhang and Dong[6],Chen[7],Liu and Ren[8],Feng et al[9],obtained,respectively,the generalization on other domains such as the bounded symmetric domains,egg domains,bounded starlike circular domains,and the unit ball in Banach spaces.In 2010,and Nechita[10]introduced the definition of almost starlike mapping of complex order λ(λ ∈ C,Reλ ≤ 0)on Bn,this new subclass of normalized locally biholomorphic mappings is the extension of starlike function of complex order[11]on the unit disk D⊆C.And they also obtained the equivalent characterization of almost starlike mapping of complex order λ by Löewner theory in[10](also see[12]).In this article,we give the sharp growth theorem for the almost starlike mapping of complex order λ on the unit ball B in finite dimensional complex Banach space X.As the application of the above result,the distortion theorem for almost starlike mapping of complex order λ along a unit direction was obtained.Various particular cases will be also considered.
In geometric theory of one complex variable,Löewner theory play an important role in the theory of univalent functions.It was first established by Löewner[13]and then developed by Kufarev[14].In 1974,Pfaltzgra ff[15]generalized Löewner theory to higher dimensions,and he also characterized the univalent of biholomorphic mappings in several complex variables by Löewner theory.Later contributions permitting generalizations to the unit ball of a finite dimensional complex Banach space were made by Poreda[16].Finally,some best-possible results concerning the existence and regularity theory of the Löewner equation in several variables can be seen in the article[17–20].As the application of Löewner theory on the unit ball of finite dimensional complex Banach space,the conclusions of this article were obtained.
2 Definitions and Lemmas
To illustrate the main results of this article,we will give some necessary definitions and lemmas.
Definition 2.1([10,12]) Let f:B→X be a normalized locally biholomorphic mapping on B,and let λ ∈ C with Reλ ≤ 0.If

then f is called to be almost starlike mapping of complex order λ.
Definition 2.2Suppose that f,g∈H(Bn).If there exist a holomorphic mapping ω :Bn→ Bnwith ω(0)=0 such that f(z)=g(ω(z)),then we say that f is subordinate to g,written
Obviously,if g is a univalent mapping on Bnin Definition 2.2,then

Definition 2.3If f:Bn×[0,+∞)−→Cnsatisfies the following conditions
(1) f(·,t)∈ H(Bn),f(0,t)=0,and Df(0,t)=etI, ∀ t≥ 0;
then we say f is a subordination chain.If f(·,t)is also a univalent mapping on the unit ball Bn,then f is called a Löewner chain.
Lemma 2.4([10,12]) Let f be a normalized locally biholomorphic mapping on B,and let λ ∈ C with Reλ ≤ 0.Then,f is a almost starlike mapping of complex order λ on B if and only if
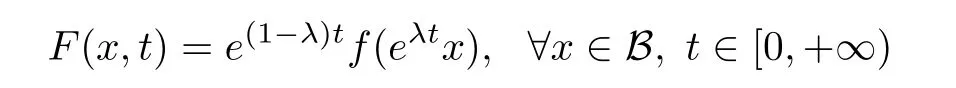
is a Löewner chain.
Lemma 2.5([9]) Let x:[0,+∞)→ X be differentiable at the point s∈(0,+∞),and let kx(t)k be also differentiable at the point s with respect to t.Then,
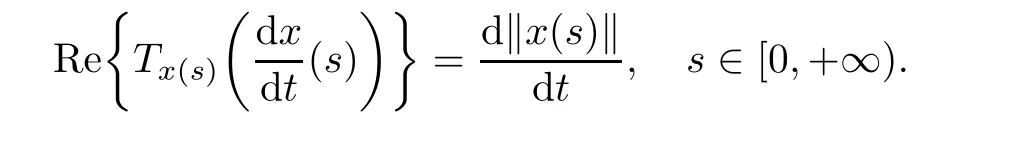
Lemma 2.6([21]) Let g:D → C be a holomorphic function with g(0)=1 and Reg(ζ)≥0,then
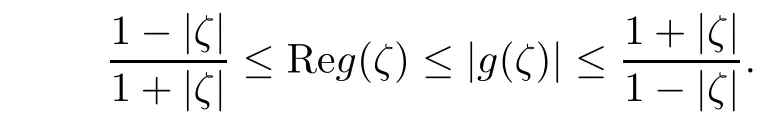
Lemma 2.7([21]) Let f(x,t)be a Löewner chain and let v(t)=v(x,s,t)be the transition mapping associated to f(x,t).If h:B×[0,+∞)→X satisfy the following conditions:(1)for each t≥ 0,h(·,t)∈ M;(2)for each x ∈ B,h(x,t)is measurable in t,and for a.e.t≥ 0,

then for each s≥0 and x∈B,v(t)satisfies the initial value problem
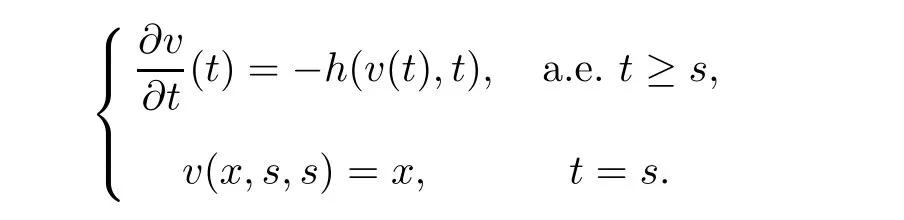
Lemma 2.8Let λ ∈ C with Reλ ≤ 0,and let f:B → X be a almost starlike mapping of complex order λ on B.Then,

and

ProofFixed x∈B{0},letThen,the holomorphic function
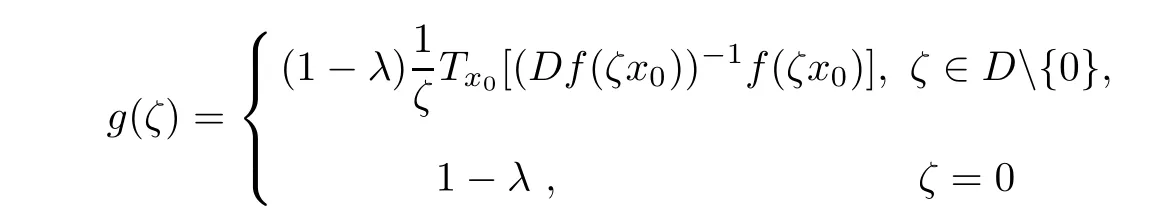
is well define on the unit disk D.Because
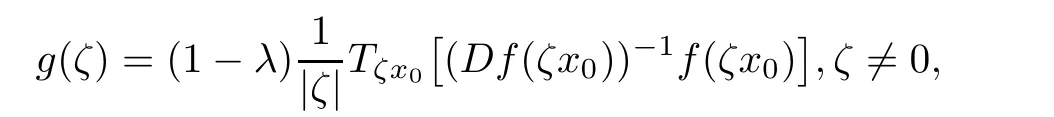
and f is a almost starlike mapping of complex order λ,hence we have

Let p(ζ)=g(ζ)+ λ.Then,Rep(ζ)≥ 0 and p(0)=1.Hence,by Lemma 2.6,
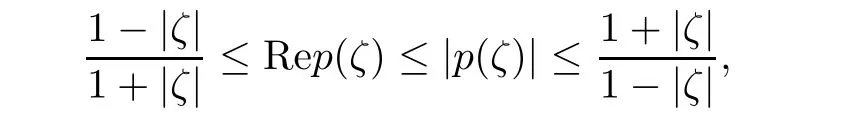
that is,
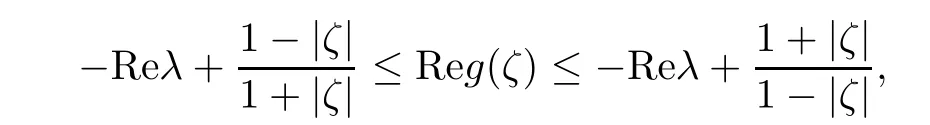
and

Let ζ=kxk,then

and
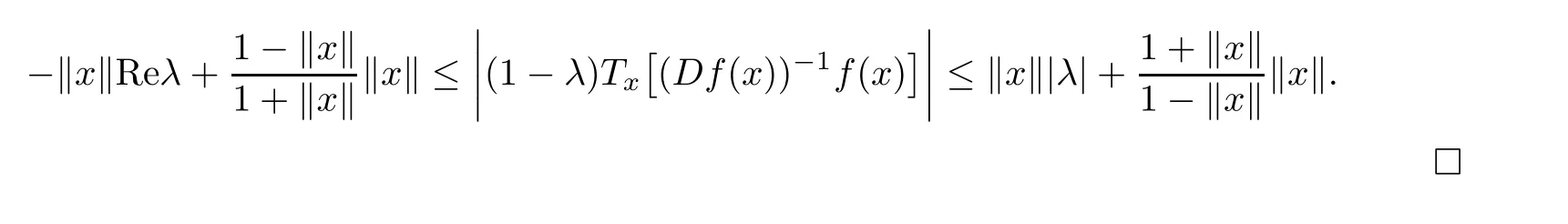
3 Main Results
Theorem 3.1Let λ ∈C with Reλ ≤ 0,and let f:B → X be a almost starlike mapping of complex order λ on B.Then,
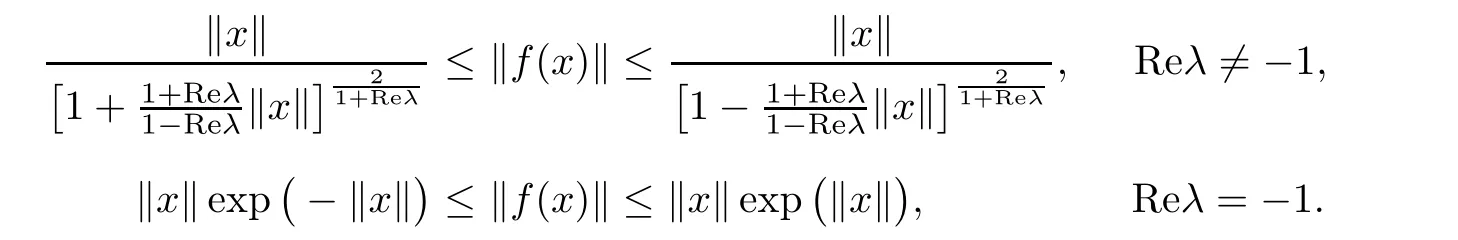
And this result is sharp.
ProofBy Lemma 2.4,it is easy to know thatis a Löewner chain,hence we havethat is,there is a Schwarz mapping v(x,s,t),called the transition mapping associated to f(x,t),such that F(x,s)=F(v(x,s,t),t).
By calculation,we have
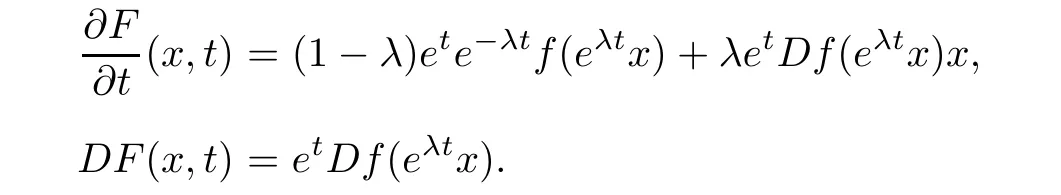

Then,h(x,t)satisfies the conditions of Lemma 2.7.And for fixed x∈B{0},s≥0,let v(t)=v(x,s,t),then
Furthermore,by Lemma 2.5,we have

hence kv(t)k is decreasing from kxk=kv(s)k to 0 as t increasing from s to+∞.By Lemma 2.8 and equality(3.1),we have
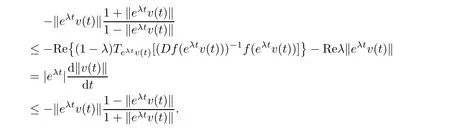
Because
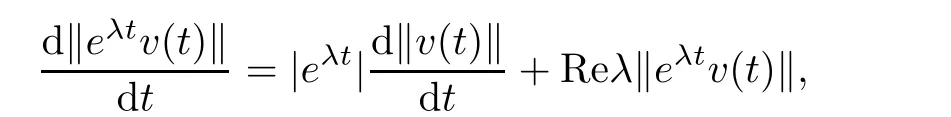
we have
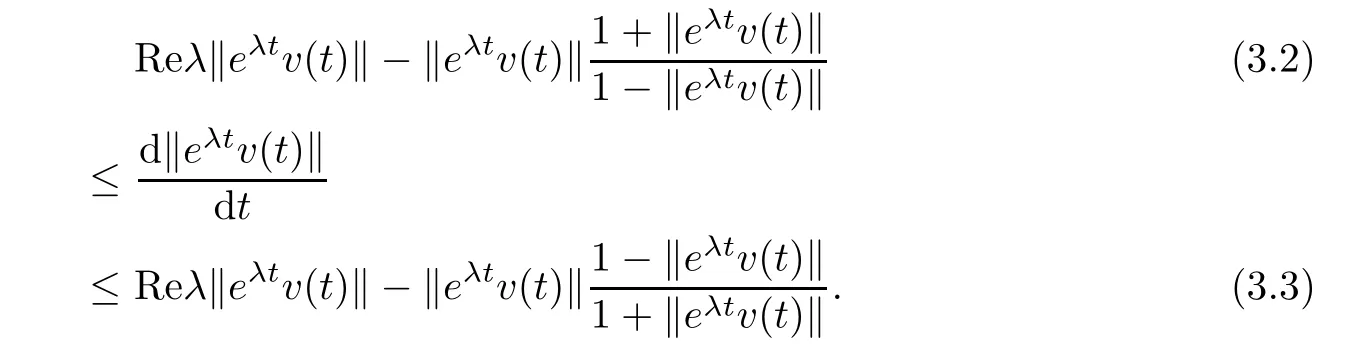
Integrating on the both sides of inequality(3.3)with respect to τ∈[s,t],we have

If Reλ 6= −1,we have
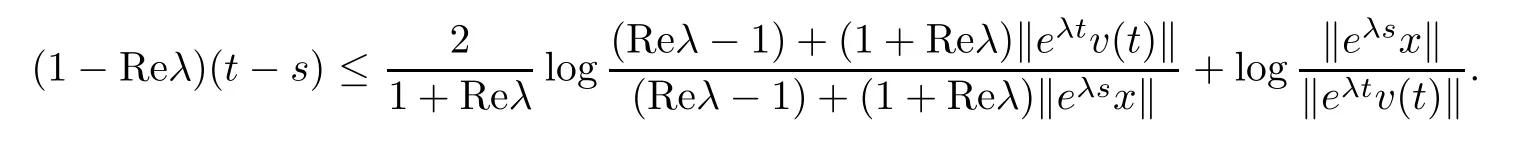
Hence,


If Reλ=−1,by inequality(3.4),we have
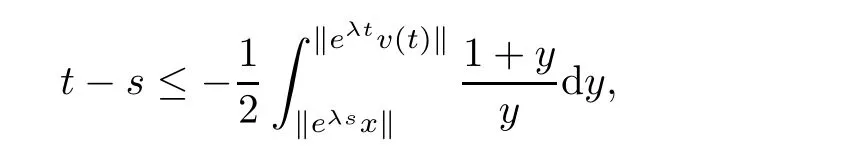
that is,
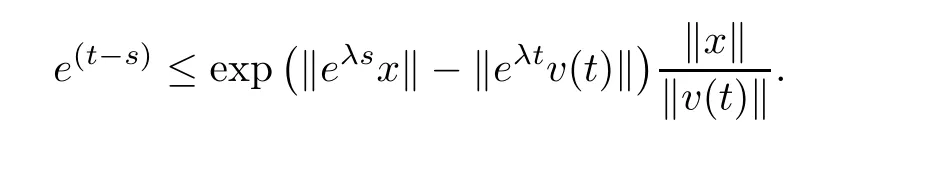
By the same reason as the above case,we have

Using the same method for inequality(3.2),we can get


in case Reλ=−1.
Next,to illustrate these result being sharp,we conside the normalized biholomorphic mappingon the unit ball,and λ ≤ 0 is a real number,where
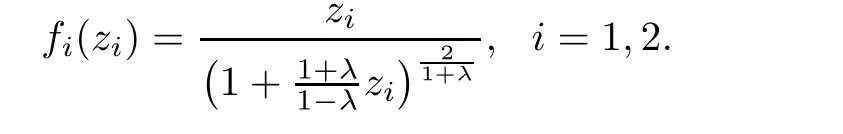
Indeed,Let B=D in Definition 2.1.Then,we have

That is to say fiis a almost starlike function of complex order λ on the unit disk D,i=1,2.By Definition 2.1,it is easy to prove that if fiis a almost starlike function of complex order λ on D,(i=1,2),then F=(f1(z1),f2(z2))′is a almost starlike mapping of complex order λ on B2.Let z1=r∈(0,1),z2=0.Then,
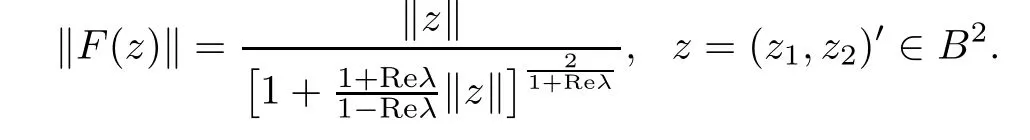
Corollary 3.2Let α ∈ [0,1),and let f:B → X be a almost starlike mapping of order α on B.Then,

And this result is sharp.
Corollary 3.3Letand let f:B → X be a spirallike mapping of type β on B.Then,
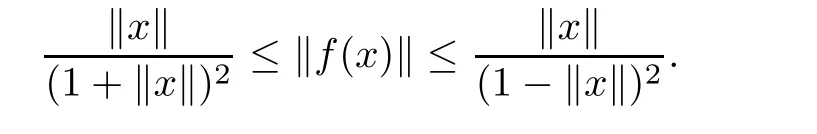
And this result is sharp.
Theorem 3.4Let λ ∈C with Reλ ≤ 0,and let f:B →X be a almost starlike mapping of complex order λ on B.Then,for all x ∈ B{0},there exists a unit vectorsuch that
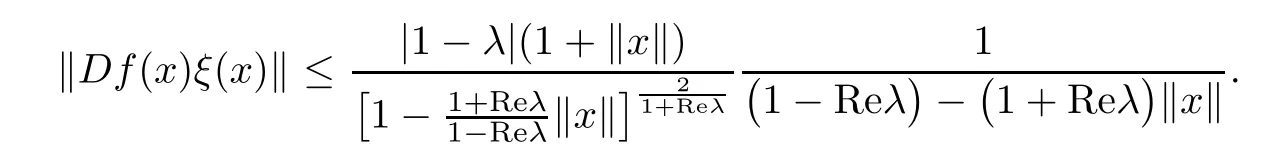
ProofLetThen,
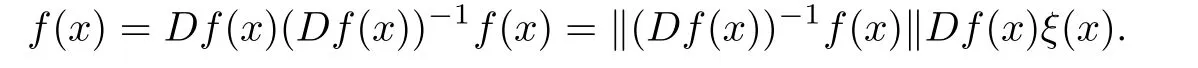
By Lemma 2.8,

hence,by Theorem 3.1 we have

Corollary 3.5Let α ∈ [0,1),f:B → X be a almost starlike mapping of order α on B.Then,for all x ∈ B{0},there exists a unit vectorsuch that
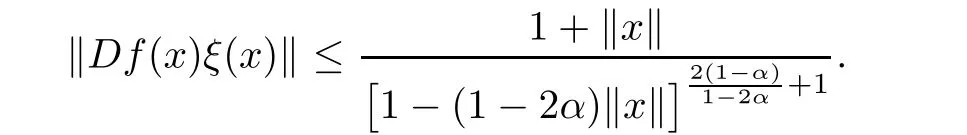
Corollary 3.6Letand let f:B → X be a spirallike mapping of type β on B.Then,for all x ∈ B{0},there exists a unit vectorsuch that
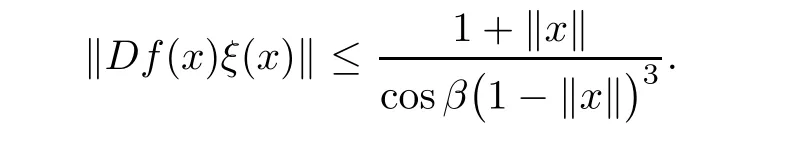
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- GLOBAL EXISTENCE OF CLASSICAL SOLUTIONS TO THE HYPERBOLIC GEOMETRY FLOW WITH TIME-DEPENDENT DISSIPATION∗
- NONNEGATIVITY OF SOLUTIONS OF NONLINEAR FRACTIONAL DIFFERENTIAL-ALGEBRAIC EQUATIONS∗
- EXACT SOLUTIONS FOR THE CAUCHY PROBLEM TO THE 3D SPHERICALLY SYMMETRIC INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
- PRODUCTS OF RESOLVENTS AND MULTIVALUED HYBRID MAPPINGS IN CAT(0)SPACES∗
- CONVERGENCE FROM AN ELECTROMAGNETIC FLUID SYSTEM TO THE FULL COMPRESSIBLE MHD EQUATIONS∗
- ON ENTIRE SOLUTIONS OF SOME TYPE OF NONLINEAR DIFFERENCE EQUATIONS∗
