基于时间反转和降阶Keystone的SAR-GMTI快速聚焦方法
2018-07-23万俊周宇张林让陈展野
万俊,周宇,张林让,陈展野
西安电子科技大学 雷达信号处理国家重点实验室,西安 710071
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种高分辨成像系统。由于其具有全天时、全天候、受环境依赖程度低等特点,广泛应用于军事/民用等领域[1-4]。然而,雷达探测场景内不可避免地存在地面运动目标。同时,雷达对于地面运动目标的检测具有重要的意义,如战场态势的评估和交通情况的监控。故将SAR技术与地面运动目标检测(Ground Moving Target Indication,GMTI)技术相结合,既可以对地面热点地区的固定目标进行观测,又可以获取运动目标的信息[5-9]。
随着雷达分辨率的提高,有效合成孔径时间的延长,场景中运动目标的距离徙动和多普勒徙动问题更加突出,导致SAR图像中运动目标散焦问题更为严重[10-11]。文献[12]提出了一种广义Radon傅里叶变换(Generalized Radon Fourier Transform,GRFT)方法,该方法通过沿目标的运动轨迹进行三维搜索,不仅能够消除运动目标距离徙动和多普勒徙动的影响,而且不受多普勒中心模糊引起的多普勒谱分裂的影响。然而,这种方法涉及多维参数化距离-方位联合搜索,尤其在较长的合成孔径时间下,其运算复杂度较高。近年来,基于Keystone变换(Keystone Transform,KT)的运动目标聚焦方法受到广泛关注[13-14]。KT可以在低信噪比环境下,实现多个目标距离徙动的统一校正,且不需要目标运动参数的先验信息。但对于存在多普勒模糊的运动目标,直接应用KT会导致目标轨迹分裂[15],影响后续的运动目标聚焦效果。为此,文献[16]提出一种1阶离散多项式变换的方法,该方法仅考虑了2阶距离模型,但并未考虑目标的机动特性。而文献[17]虽然考虑了目标的机动特性,但是其处理流程是在假设3阶距离弯曲可以忽略的情况下进行的。对于长合成孔径时间下的机动目标聚焦,3阶距离模型带来的距离徙动和多普勒徙动都会造成目标的能量沿距离维和多普勒维扩散。如果忽略它们,则都会导致能量积累的损失,严重影响最终运动目标聚焦的性能。
针对上述问题,本文提出了一种基于时间反转处理(Time Reversal Processing,TRP)和降阶KT处理的运动目标快速聚焦方法。针对地面运动目标的机动特性,建立了目标3阶距离模型。通过TRP补偿距离模型1阶项与3阶项对运动目标聚焦的影响。然后,通过构造方位时延函数进行相位降阶,结合KT校正剩余的距离走动并完成2阶项的估计。最后,利用估计得到的2阶项构造2阶相位补偿函数补偿运动目标的2阶距离弯曲和多普勒徙动,从而最终完成运动目标的聚焦。
1 信号模型
SAR平台和地面运动目标的几何关系如图1所示。对于工作在正侧视条带模式下的SAR,在合成孔径时间Ta内,平台以速度v沿y轴方向保持匀速直线飞行,地面任意点目标从点a匀加速运动到点b,其中vc、ac、va、aa分别为地面运动目标垂直平台航线速度、垂直平台航线加速度、方位向速度以及方位向加速度。
结合图1所示的几何关系,雷达平台和目标之间的瞬时斜距Rs(tm)为
(1)
式中:H为雷达平台飞行高度;X为在点a时目标到y轴的垂直距离;tm∈(-Ta/2,Ta/2)为方位慢时间变量。
对瞬时斜距进行泰勒级数展开,由于目标的机动特性,使用传统的2阶距离模型误差较大,必须考虑3阶距离模型对运动目标聚焦的影响[17]。为此忽略3阶以上的高阶项后,瞬时斜距可以表示为
(2)
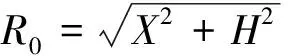
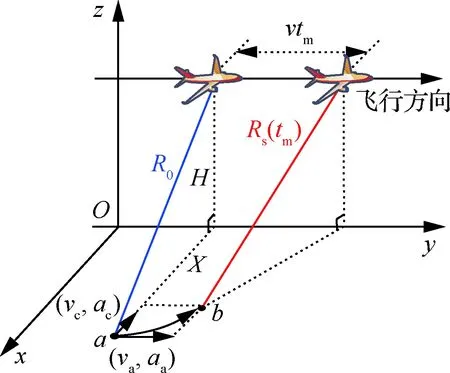
图1 SAR平台和地面运动目标的几何关系Fig.1 Geometrical relationship between SAR platform and a ground moving target
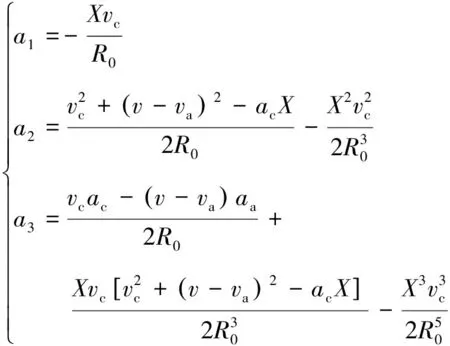
(3)
假设雷达发射线性调频信号
(4)
经过相干检波,雷达回波可以表示为
(5)
式中:c为光速;wa(tm)为方位窗函数;λ为发射信号波长。脉压处理后,回波信号可以表示为
(6)
式中:sincx=sin(πx)/(πx)为辛格函数;A1为信号幅度;B为发射信号的带宽。结合式(2),对式(6)沿距离快时间进行傅里叶变换(Fourier Transform,FT),得到脉压后回波的距离频域表达式为[18]
(7)
式中:f为距离快时间频率变量;A2为距离频域方位慢时间域的信号幅度。从式(7)可以看出,距离频率和方位慢时间存在耦合。同时,距离展开式的高阶项引入了严重的距离徙动和多普勒徙动,造成能量沿距离维和多普勒维扩散。如果不对其进行补偿,将严重影响运动目标的聚焦效果。
2 地面运动目标快速聚焦
2.1 时间反转处理
SAR系统探测目标时,场景中不可避免地出现径向快速目标,其对应的多普勒频率会大于系统的脉冲重复频率(Pulse Repetition Frequency,PRF),从而造成多普勒中心模糊与目标多普勒谱分裂,直接使用KT,会导致目标轨迹分裂,因此严重影响运动目标的聚焦[19]。
针对这一问题,本节提出一种时间反转处理方法,有效消除多普勒中心偏移(模糊)对运动目标聚焦带来的影响。不失一般性,假设方位慢时间脉冲个数M为奇数,则方位慢时间变量可以表示为[20]
tm=m·PRI
(8)

假设Mamb表示目标的多普勒模糊数,则有
(9)
式中:a0为目标的基带速度[19]。将式(9)代入式(7)中可以得到

(10)
对式(10)进行慢时间反转得到
(11)
将式(10)和式(11)相乘得
(12)
从式(12)可以看出,在距离频域方位慢时间域进行TRP后,由1阶项引起的距离走动与多普勒中心模糊和3阶项引起的3阶距离弯曲与多普勒徙动,得到了有效补偿。本方法对于模糊数不为0的快速目标而言依然有效,同时没有模糊速度搜索过程,提高了对快速目标的适应性。同时,算法仅需要点乘操作,故具有较高的计算效率。
2.2 降阶Keystone变换处理
由式(12)可得,虽然方位慢时间TRP消除了1阶项与3阶项对运动目标聚焦的影响,但2阶项引起距离弯曲和多普勒徙动依然存在。
为此,本节首先构造方位时延降阶函数
(13)
式中:τ0为固定时延。从式(13)中可以看出经过相位降阶后,原信号变为一个单频信号。与此同时,该过程又引入了新的距离走动。由于固定时延通常较小,式(13)中的等效1阶项通常小于基带速度[16-17]。
此时,直接利用KT可以补偿式(13)中的距离走动,该过程既不需要搜索多普勒模糊数,也不会导致目标轨迹分裂。对式(13)应用KT后,可以得到
(14)
式中:τm为Keystone变换后的慢时间变量。
对式(14)进行距离频域逆傅里叶变换(Inverse Fourier Transform,IFT)和方位慢时间FT后,信号表达式为
(15)
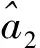
(16)
结合式(16),在距离频域方位慢时间域构造的相位补偿函数为
(17)
将式(12)与式(17)相乘可以得到
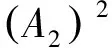
(18)
对式(18)进行距离频域IFT和方位慢时间FT之后可以得到
(19)
式中:A3为信号幅值;fa为方位多普勒变量。从式(19)可以看出运动目标能量在距离多普勒域得到有效聚焦。所提方法流程图如图2所示。
由于上述分析是在方位慢时间满足对称性的情况下进行的,当方位慢时间不满足对称性时本方法的有效性证明详见附录A。

图2 所提方法流程图Fig.2 Flow chart of proposed method
3 算法性能分析
3.1 多目标聚焦
实际应用中,雷达探测的场景中通常存在多个运动目标。此时,距离频域方位慢时间域的回波信号为
(20)
式中:k为目标个数;A2i为第i个目标的信号幅值;R0i为第i个目标的最近斜距;a1i、a2i和a3i分别表示第i个目标的1阶、2阶和3阶项系数。
对式(20)进行方位慢时间TRP,得到表达式为
T1-cross(f,tm)
(21)
式中:T1-cross(f,tm)表示交叉项,其具体表达式由附录B中的式(B1)结出。
对式(21)构造方位时延降阶函数进行相位降阶得到新的信号为
(22)
式中:T2-cross(f,tm)表示交叉项,其具体表达式由附录B中的式(B2)给出。
对式(22)进行KT得到的表达式为
(23)
式中:T3-cross(f,τm)表示交叉项,其具体表达式由附录B中的式(B3)给出。
从式(23)可以看出只有自聚焦项的距离走动得到校正,其能量落在同一个距离单元内,而交叉项的距离徙动和多普勒徙动依然存在。所以交叉项并不会影响2阶参数的估计。同理,从式(21)可以看出,只有自聚焦项的1阶和3阶项引起的距离徙动和多普勒徙动可以得到校正,而交叉项的距离徙动和多普勒徙动依然存在。由于使用相位补偿函数补偿2阶项引起的距离弯曲和多普勒徙动是一个线性过程,所以所提方法对多目标聚焦依然有效。
3.2 方法计算复杂度
令N、L、N1、N2、N3分别为距离单元个数、方位脉冲个数、1阶项搜索数目、2阶项搜索数目、3阶项搜索数目。所提方法对运动目标聚焦时,主要涉及一次TRP、一次方位慢时间相位降阶、一次KT和一次2阶项相位补偿。其中,本文使用非插值方式实现KT,其计算复杂度[21]为O(4NLlog2L),因此,所提方法的运算复杂度为O(4NLlog2L+3NL)。另一方面,基于3维搜索方法GRFT的计算复杂度为O(N1N2N3NL),文献[13]方法主要涉及一次KT、一次距离弯曲匹配滤波、一次NL点复乘、Na次速度模糊数搜索。由于文献[13]使用插值方式实现KT,所以该方法的计算复杂度为O[NL2+L(L-1)N+(2+Na)NL]。文献[16]主要涉及一次离散多项式变换、两次KT、一次距离弯曲补偿、Nb次速度模糊数搜索。文献[16]同样使用非插值方式实现KT,其计算复杂度为O[8NLlog2L+(2+Nb)NL]。通过表1的计算复杂度对比可知本文方法的计算复杂度最低。
假设1阶项的搜索范围为(-10,10),2阶项的搜索范围为(-5,5),3阶项的搜索范围为(-1,1),模糊速度搜索次数Na=Nb=5,距离单元数N=500,SAR系统仿真参数如表2所示。图3给出了4种方法计算复杂度与方位脉冲个数的变化曲线。由图3可以看出搜索方法GRFT的计算复杂度远大于另外3种方法,而采用插值方法实现KT的文献[13]方法比本文方法大一个数量级以上。由仿真可以得出当方位脉冲个数为3 000时,即使同样使用非插值实现KT,文献[16]方法的计算复杂度比本文方法高102.03%。以上都可以说明本文方法在计算速度上的优越性。

表1 计算复杂度对比Table 1 Comparison of computational complexity

表2 SAR系统仿真参数Table 2 Simulation parameters of SAR system
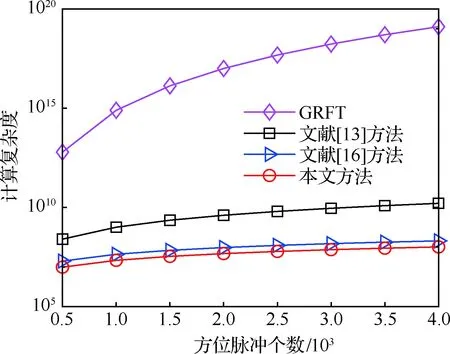
图3 4种方法计算复杂度随方位脉冲个数变化曲线Fig.3 Curves of computational complexity vs integration pulse number with four methods
4 计算机仿真与分析
为了验证所提方法的有效性,设计了3个仿真实验,仿真使用的SAR系统参数如表2所示。
同时,仿真过程假设回波信号杂波已经得到了有效抑制[8,22]。
4.1 仿真实验1
本实验主要用于验证所提方法的有效性。实验中目标A参数设定为:vc=-30 m/s,va=-8 m/s,aa=3 m/s2,ac=1.2 m/s2,固定时延τ0设置为0.25Ta[23]。仿真在高斯白噪声背景下进行,回波信噪比设置为-6 dB。仿真结果如图4所示。其中图4(a)为距离脉压后目标的轨迹,可以看出由于目标的机动特性,目标的轨迹在脉压后产生了明显的距离徙动现象。对图4(a)距离脉压后的信号进行方位慢时间FT得到如图4(b)所示的结果,可以看出目标信号跨越多个多普勒单元,由于目标的径向速度较大,目标的多普勒谱产生了分裂现象。图4(c)为距离频域方位慢时间域TRP后的结果。可以看出目标的1阶和3阶距离徙动已经得到有效的校正,但是2阶距离弯曲和多普勒徙动依然存在。图4(d)为对图4(c)的结果进行方位慢时间相位降阶的结果,可以看出目标的距离弯曲已经消除,但是又引入了距离走动。对图4(d)的结果进行KT校正目标的距离走动,结果如图4(e)所示,可以看出目标的距离走动已经得到校正,目标的信号能量落在同一个距离单元中。随后进行方位慢时间FT累积能量和2阶项运动参数估计,结果如图4(f)所示,估计得出的2阶项系数为1.487 5,实际值为1.486 8,可以计算出2阶参数的估计误差百分比(误差值比实际值)为0.05%。图4(g)和图4(h)为构造2阶相位补偿函数补偿2阶距离弯曲和多普勒徙动后进行方位慢时间FT累积的结果,可以看出目标的能量经过FT累积后可以形成明显的峰值。

图4 所提方法聚焦结果Fig.4 Focusing results of proposed method
4.2 仿真实验2
本实验用来比较所提方法与文献[13,16]快速方法的性能。结果如图5所示。其中图5(a)和图5(b)表示所提方法的聚焦结果及峰值,可以发现由于所提方法准确补偿了目标的距离徙动和多普勒徙动。目标的能量可以得到较好的聚焦,其能量累积效果较好。图5(c)和图5(d)表示使用文献[13]中方法得到的聚焦结果及峰值,由于该方法对2阶距离弯曲近似补偿,且并未考虑3阶距离模型的影响。目标的能量在距离多普勒域不能得到较好的累积。图5(e)和图5(f)表示文献[16]方法得到的运动目标聚焦结果及峰值。由于该方法可以补偿目标的1、2阶项引起的距离徙动和2阶项引起的多普勒徙动,但未能补偿3阶项引起的距离徙动和多普勒徙动,即目标能量在距离多普勒域扩散。所以,使用该方法目标的能量在距离多普勒域不能得到较好的累积。由仿真参数可以计算出目标的2阶项实际值为1.487 5,利用所提方法得到的2阶项估计值为1.486 8,估计误差百分比为0.05%。而文献[16]方法得到的2阶项估计值为1.388 3,估计误差百分比为6.63%。可以说明所提方法的聚焦性能较好。因此,以上都说明了所提方法的优越性。
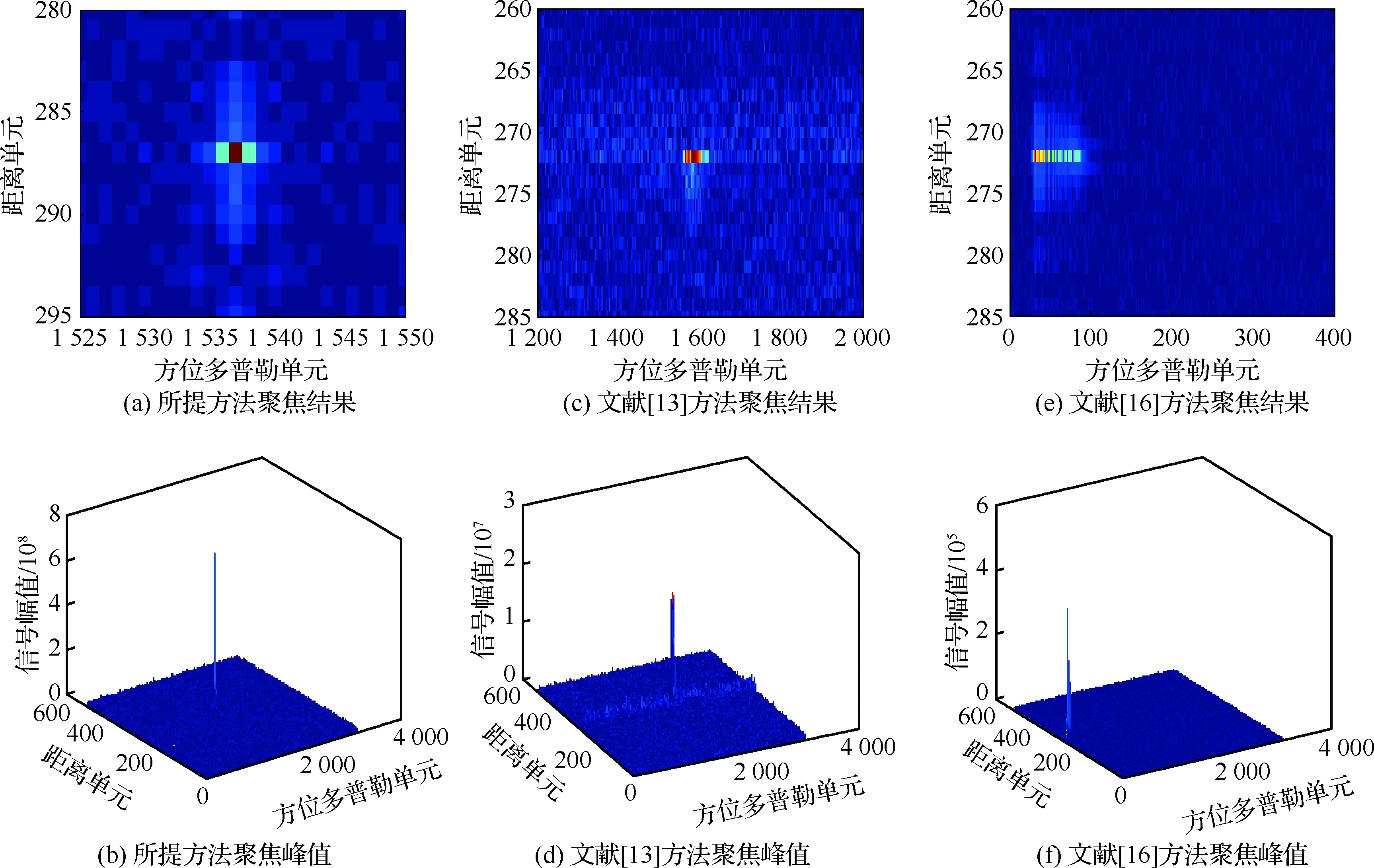
图5 3种不同方法聚焦结果及峰值Fig.5 Focusing results and peak values of three methods
4.3 仿真实验3
本实验用来验证所提方法多目标的交叉项抑制性能。为了方便简化分析,不失一般性,仿真场景设置两个运动目标[16]。其中,目标B的参数设定为:vc=30 m/s,va=4.6 m/s,aa=1 m/s2,ac=3 m/s2,目标A与实验1一致。仿真结果如图6所示。图6(a)为距离脉压后目标A和目标B的运动轨迹,可以发现由于两个目标机动特性的影响,两个目标的轨迹都产生了明显的距离徙动现象。图6(b)为对脉压后的信号进行距离频域方位慢时间TRP的结果。可以发现自聚焦项A和自聚焦项B的1阶和2阶距离徙动已经得到补偿,但是2阶距离弯曲依然存在,而交叉项则存在不规则的距离徙动。图6(c)为方位相位降阶和KT后的结果,可以发现自聚焦项的距离徙动都得到校正,能量落在同一个距离单元,而交叉项存在不规则的距离徙动能量分布在不同的距离单元内。所以,在进行方位慢时间FT时,自聚焦项的能量可以得到很好的累积而交叉项的能量却不能得到很好的累积,结果如图6(d)所示。所以,仿真验证了所提方法对多目标同样有效。
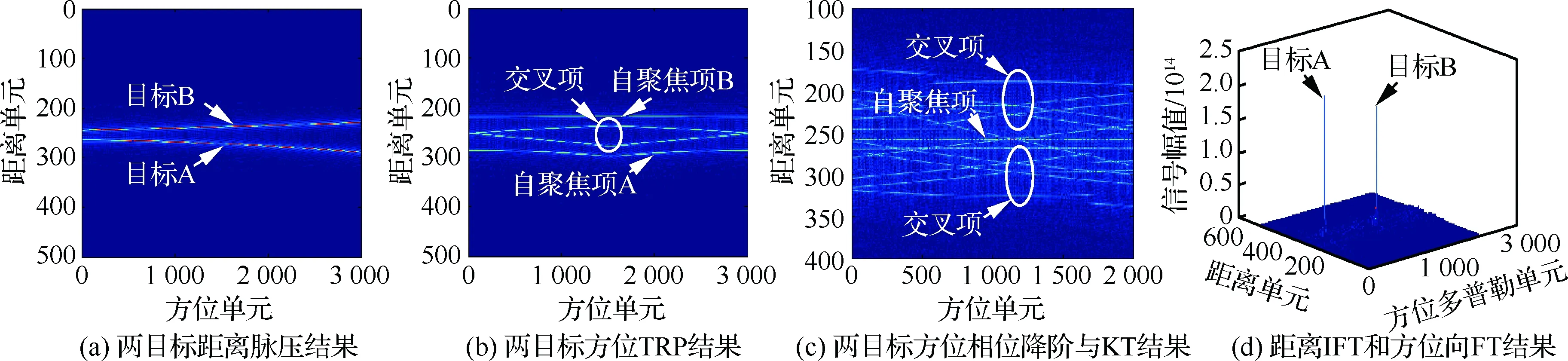
图6 两目标聚焦结果Fig.6 Focusing results of two targets
5 结 论
1) 研究了合成孔径雷达地面运动目标快速聚焦方法。针对运动目标的机动特性,建立了运动目标3阶距离模型,提出了一种基于时间反转和降阶Keystone的SAR-GMTI快速聚焦方法。
2) 理论分析与仿真实验验证表明,所提方法有效地解决了运动目标的距离徙动和多普勒徙动引起的散焦问题,且不受多普勒中心模糊引起的多普勒谱分裂的影响,同时没有任何参数搜索过程,降低了计算复杂度。
s1(f,tm+Δt)s1(f,-tm+Δt)=
[2a1Δt+2a2Δt2+2a3Δt3+
(A1)
由式(A1)可以看出即使慢时间不满足对称性,通过时间反转处理同样可以消除1阶和3阶项。对式(A1)信号进行降阶KT处理后,执行距离频域IFT,方位慢时间域FT可以得到非对称时,式(15)忽略常数项表示为
(A2)
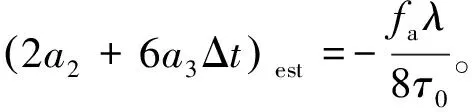
通过构造相位补偿函数后,非对称时,式(19)的聚焦表达式忽略常数项为
s4(t,fa)=sinc{B[t-
4(R0+a1Δt+a2Δt2+a3Δt3)/c]}·
sinc (Tafa)
(A3)
由式(A3)可以看出,慢时间非对称并不影响所提方法的聚焦性能。
附录B:
式(21)中的交叉项忽略常数项可以表示为
(B1)
式(22)中的交叉项忽略常数项可以表示为
(B2)
式(23)中的交叉项忽略常数项可以表示为
(B3)
