内外流共同作用下输流软管力学特性研究

李 艳， 成 赟， 郭轶可， 刘少军

(1.中南大学 机电工程学院， 湖南 长沙 410083； 2.深海矿产资源开发利用技术国家重点实验室， 湖南 长沙 410012)

1 研究背景

随着社会发展对资源的需求越来越大，人类开始迈步海洋探索其中蕴藏的资源，深海采矿系统的研究成为世界各国在海洋装备研究领域的一个热点课题。我国计划在“十三五”期间完成1 000 m级海上采矿试验，同时开展更深级别深海采矿试验系统和成套技术装备的研制[1]。国内外专家学者提出了多种采矿系统类型，总体来说，管道水力提升式采矿系统更适用于现代化的商业开采[2]。图1是中国1 000 m级深海采矿系统的示意图，包括采矿船、提升泵、输流硬管、输流软管、中间仓和集矿车等装置[3-4]。在深海采矿扬矿子系统中，输流软管是一个很重要的组成部分，是矿浆从集矿车流向中间仓的通道，同时又是控制电缆和信号电缆等的附着体。输流软管的工作状态不仅受内流速度、密度等因素的影响，同时还受外部工作环境中海流流速等因素的影响。在内部矿浆和外部海流的共同作用下，可能使输流软管的应力、应变、构型等发生较大的变化，从而影响输流软管的正常工作，导致整个深海采矿系统不能正常运转。因此，考虑多因素耦合影响下，深海采矿输流软管的力学特性是非常有必要的。

Oh等[5]研究了外流作用下输流软管与中间仓连接处的应力大小，分析了不同联接方式对输流软管最大主应力的影响。Wang Zhi等[6]运用Marc三维有限元软件研究了柔性管内部矿浆浓度、内流提升速度和柔性管弹性模量等因素变化对流体阻力损失变化的影响。Peng等[7]研究了柔性管空间初始构型、内部矿浆浓度和柔性管出入口相对位置等因素对柔性管运输的临界速度和管中压力降的影响。王刚等[8]基于空间管梁模型单元耦合建模方法，建立了扬矿管线的力学分析耦合模型，分析了深海采矿柔性管的水下空间形态。Ruan Weidong等[9]建立模型研究了海洋环境载荷和弹性海底对Lazy-wave构型深海电缆静力学行为的影响。简曲等[10]运用离散元法把输流软管简化成为空间梁单元，分析了输流软管在外界因素影响下的空间形态、位移和应力变化。张伟等[11]利用ABAQUS有限元软件，考虑周围海洋环境载荷的影响，对钢悬链线立管进行了有限元动力学响应分析。国内外学者做了众多相关研究，但均未考虑内外流共同作用下输流软管的流固耦合特性。

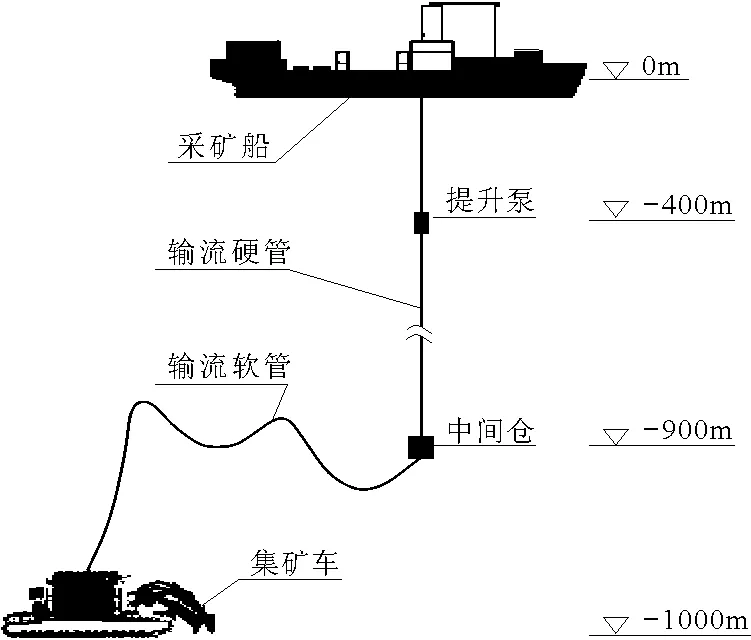
图1 1 000 m深海采矿系统示意图

本文以中国1 000 m级深海采矿系统为背景[12]，在如图2深海采矿输流软管已有马鞍型平衡构型的基础上[13]，利用ANSYS Workbench平台建立了考虑内、外流的输流软管三维流固耦合有限元模型，对内、外流共同作用下的输流软管进行流固耦合数值分析，研究内、外流因素对输流软管力学特性的影响，以便为后续深海输流软管的设计及工况参数的选择提供基础依据。

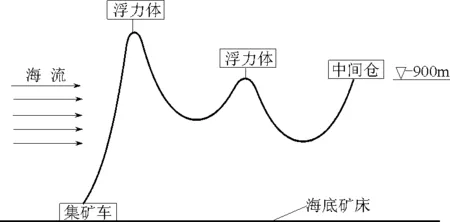
图2 输流软管构型示意图

2 计算模型

2.1 输流软管受力分析

在深海扬矿过程中，输流软管会受到自身的重力GR，内部矿浆重力GL，内部矿浆流体作用力FN，海水浮力FS，浮力体浮力FF，中间仓和集矿车的拖拽力FZ、FC，海洋海流力FH等多种复杂载荷的共同作用。输流软管受力示意图如图3所示。

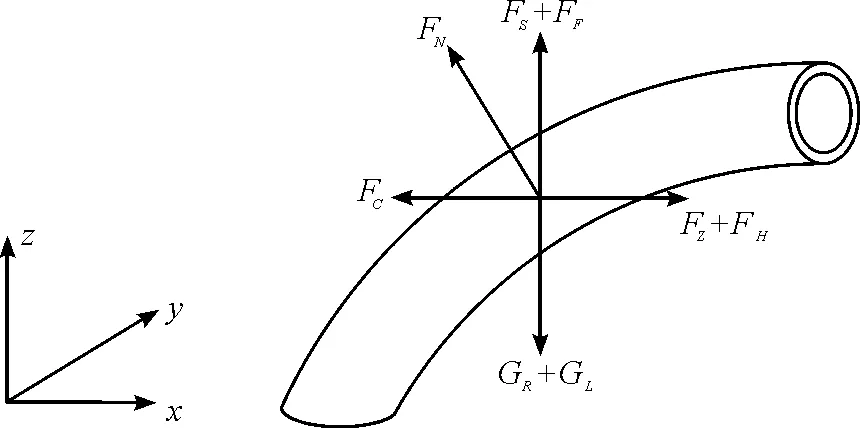
图3 深海采矿系统中输流软管受力示意图

输流软管自身重力为：

(1)

内部矿浆流体重力为：

(2)

海水浮力为：

(3)

浮力体浮力为：

FF=GR+GL-FS

(4)

式中：ρr、ρi、ρo分别为输流软管的密度，内部矿浆密度，海水密度；D0、Di分别为输流软管的外径和内径；L为输流软管的总长度。

2.2 输流软管流固耦合数学模型

输流软管与内、外部流体是相互影响的，内、外部流体的作用力分别施加到内、外管壁上，引起输流软管的变形，输流软管的变形反过来会影响流体区域，这样就形成了流固耦合过程。建立输流软管与内、外流体的流固耦合控制方程如下：

2.2.1 流体控制方程 假设内外部流体均为不可压缩的黏性流体，依据计算流体力学理论，针对低速不可压缩黏性流体运动问题，其N-S运动控制方程为[14-15]：

(5)

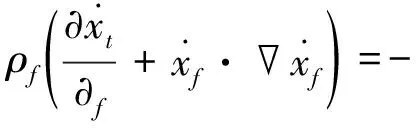
(6)

2.2.2 结构控制方程 假设输流软管为线弹性结构，采用空心梁模型。内外流流动产生的作用力分别作用在输流软管的内外壁面上，输流软管相对于其平衡位置做刚体运动和发生弹性变形，输流软管运动控制方程为[16-17]：

(7)

式中：[M]为结构质量矩阵； [C]为结构阻尼矩阵； [K]为结构刚度矩阵； {xr}为位移列阵； {F}为外界各种力合成的等效列阵。

2.2.3 边界条件 流固耦合遵循最基本的守恒原则，内外部流体与输流软管之间的流固耦合面为非滑移壁面，在内外流固耦合面上位移和应力分别相等[18-19]，应力分布情况相同。

流固耦合边界位移相容方程：

xf=xr

(8)

流固耦合边界应力平衡方程：

τf·nf=τr·nr

(9)

在流体计算中，常常以速度作为求解的基本量。因此，式(8)的位移相容方程可以进一步改写为速度相容方程。

(10)

内外部流体和输流软管之间的相互作用力FI根据反馈计算[20-21]：

FI(S1,S2,t)=-k[(xi-xr)+Δt(vi-vr)]

(11)

式中：k是大数恒量;Δt是计算时间步；xi,vi分别是流固耦合边界的位置和速度；xr,vr分别是输流软管计算点的位置和速度。则得到的流固耦合相互作用力FI可用于力密度f和输流软管运动控制方程(7)的求解。

运用浸入边界法将流体在流固耦合面处受到的相互作用力使用Dirac delta函数做卷积形式变换，得到流场中的力密度f[22]:

(12)

式中：xi(S1,S2,t)为流固耦合边界位置；FI(S1,S2,t)为流固耦合边界处的相互作用力，则得到的力密度f可用于N-S方程(6)的求解。

3 仿真与分析。

3.1 输流软管流固耦合仿真模型

综合考虑输流软管周围海流和内部矿浆的流动特性，在输流软管现有马鞍型平衡构型基础上，通过ANSYS Workbench平台进行建模仿真计算。输流软管及内部流体按表1中参数建立马鞍型模型，外部流体包围整个输流软管，为了保证计算结果不受外流边界的影响，考虑计算的精确性和时间成本，建立450 m×200 m×300 m足够大的外流长方体模型。输流软管和内、外部流体的三维流-固耦合模型，如图4和图5所示。

表1 400 m输流软管参数

深海采矿输流软管两端分别与集矿车和中间仓相连，仿真计算时，输流软管两端采用固定约束，内、外部流体产生的流固耦合力，通过设置的非滑移流固耦合面，分别加载到输流软管的内、外壁面上。求解理论流程如图6所示，基于ANSYS Workbench平台求解实现过程如图7所示。通过改变内流速度、海流速度等参数进行数值模拟，研究内、外流共同作用下输流软管的流固耦合力学特性。

图4 输流软管和内部流体三维流固耦合模型

图5 输流软管和外部流体三维流固耦合模型

3.2 内外流共同作用下内部流体对输流软管的影响

在研究内流速度对输流软管流固耦合特性的影响时，在流体模块中依次设置内流速度为2.0，3.0，4.0，5.0，6.0，7.0，8.0 m/s。输流软管的空间最大位移在不同内流速度下时间历程曲线如图8所示，峰值最大位移与稳态最大位移的差值和到达稳态的时间都随着内流速度的增加而减小。

图6 流固耦合求解流程

图7 流固耦合求解模块关系图

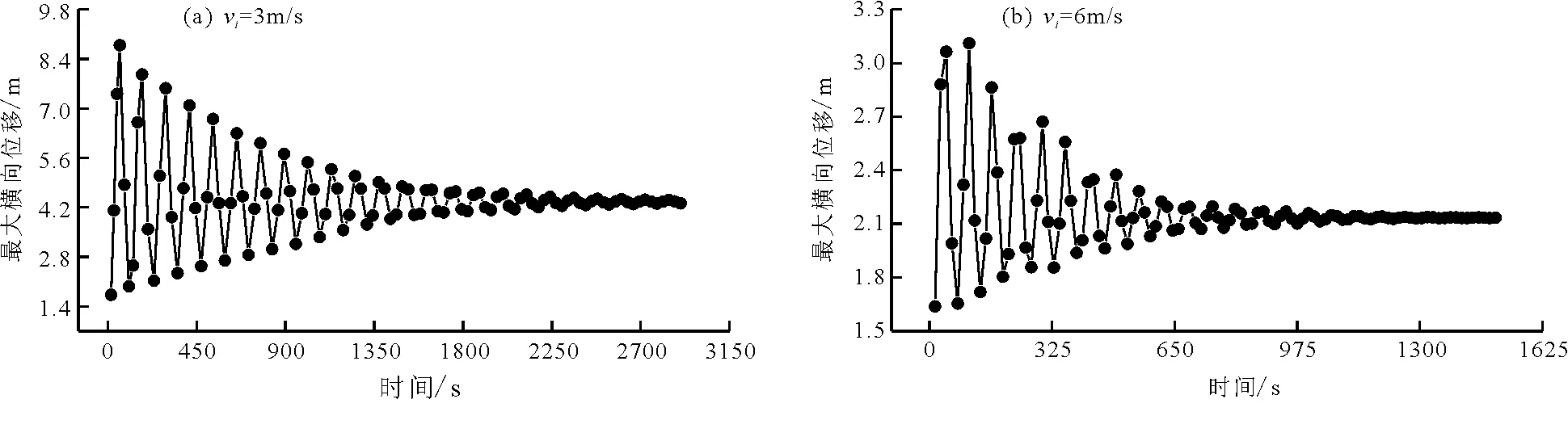
图8 不同内流速度下软管空间位移时间历程曲线

内流速度对输流软管流固耦合力学特性的影响如图9和图10所示。由于内流速度的增加，会对外流影响下的输流软管位移产生更显著的抑制作用。随着内流速度的增大，输流软管最大横向位移减小。输流软管在内流速度大于4 m/s时的最大横向位移变化幅度明显减小，这是由于内流对管壁产生的作用力主要出现在靠近集矿车，输流软管的入口处，随着内流速度的增大，采矿车对输流软管的拖拽力增大，从而使得输流软管最大横向位移的变化趋于平滑、输流软管的最大横向位移趋于稳定。随着内流速度的增大，输流软管的最大主应力先减小后增大，这是由于内流速度小于4 m/s时，外流是影响最大主应力的主要因素，使得输流软管的最大主应力位于与中间仓连接处；当内流速度大于4 m/s时，内流是影响最大主应力的主要因素，使得输流软管的最大主应力位置转移到了与集矿车连接处。内流速度影响下输流软管构形变化如图11所示，当内流速度大于3 m/s时，软管位移更稳定，随内流速度增大构型变化比较小。为了保证矿浆可以安全、连续、平稳地输送，输流软管两端连接处的主应力不宜太大，集矿车和中间仓受到输流软管的影响应尽可能的小，所以内流速度保持在3～6 m/s之间更为合理。

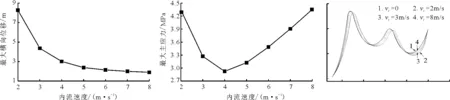
图9软管最大横向位移与内流流速关系图10软管最大主应力与内流流速关系图11软管构型与内流流速关系

在研究内流密度对输流软管流固耦合特性的影响时，在流体模块中依次设置内流密度为1 000，1 200，1 400，1 600，1 800，2 000 kg/m3。内流密度对输流软管流固耦合力学特性的影响如图12和图13所示。随着内流密度的增大，输流软管的最大横向位移减小，并且在内流密度大于1 200 kg/m3时，输流软管最大横向位移的变化幅度有所减小。这是由于随着内流密度的增大，内流的影响增大，在内外流共同作用下软管的位移减小；并且由于内流对管壁产生的作用力主要出现在靠近集矿车端，输流软管入口处，随着内流速度的增大，集矿车对输流软管的拖拽力增大，从而使得输流软管最大横向位移的变化幅度有所减小。随着内流密度的增大，输流软管最大主应力增大，并且内流密度小于1 200 kg/m3时，最大主应力的变化幅度小于内流密度大于1 200 kg/m3，这是因为当内流密度小于1 200 kg/m3时，外流是影响最大主应力的主要因素，其最大主应力位于与中间仓连接处，当内流密度大于1 200 kg/m3时，内流对输流软管的影响增强，其最大主应力位置转移到了与集矿车连接处。所以经过集矿机对深海矿物进行脱泥和破碎，保证内流密度在一个相对稳定的范围，避免由于内流密度变化范围太大引起输流软管位移和应力大范围变化，对于整个扬矿系统是非常重要的。

3.3 内外流共同作用下周围海流对输流软管的影响

在海洋垂直面上海流的速度随海水深度的变化而变化，根据我国勘察的试采区，海洋表面速度为0.772 m/s，海底流速为0.15 m/s。海流速度随深度变化曲线如图14所示。在研究周围海流速度对输流软管流固耦合特性的影响时，假设周围海流沿水平方向从集矿机一端流向中间仓一端，海流方向如图2中箭头所示。在流体模块中依次设置海流速度为0.15，0.30，0.45，0.60，0.75 m/s。输流软管的空间最大位移时间历程曲线如图15所示，峰值最大位移与稳态最大位移的差值和到达稳态的时间都随着海流速度的增加而增大。

图12软管最大横向位移与内流密度关系图13软管最大主应力与内流密度关系图14海流速度与海洋深度关系

海流速度对输流软管流固耦合力学特性的影响如图16和图17所示。随着海流速度的增大，输流软管的最大横向位移和最大主应力都增大，并且海流速度大于0.3 m/s时，输流软管的最大横向位移和最大主应力的增幅有所变大。由于海流速度的增大，使得输流软管沿海流方向前后两侧流体域产生的压差增大，流体阻力增幅随之增大，输流软管的最大横向位移和最大主应力也随之增大。海流速度影响下输流软管构形变化如图18所示，当海流速度大于0.3 m/s时，靠近中间仓端输流软管的构形变化明显，与中间仓连接处出现折弯。为了保证输流软管有相对稳定的空间构形，从而尽可能小的影响整个扬矿系统的稳定，输流软管更适合在海流速度小于0.3 m/s的海水环境中工作。

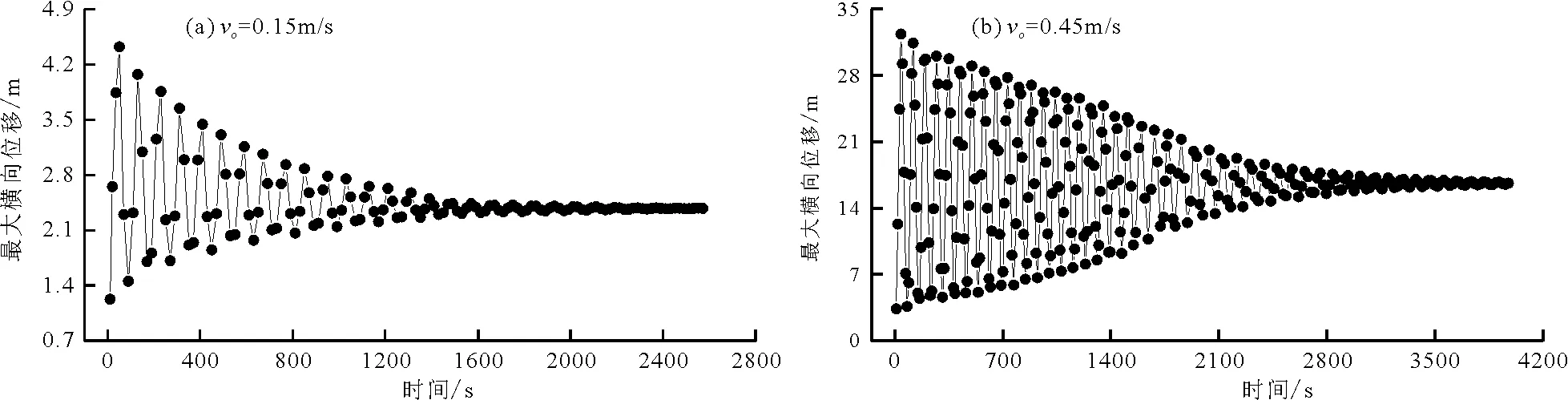
图15 软管空间位移时间历程曲线

图16 软管最大横向位移与外流流速关系 图17 软管最大主应力与外流流速关系 图18 软管构形与外流流速关系

4 结 论

(1)随着内流速度的增大，输流软管的最大横向位移减小、最大主应力先减小后增大。当内流速度大于3 m/s时，输流软管的空间构型相对更为稳定。同时，为了保证输流软管的最大主应力在工作过程中不会太大，内流速度不易过大。应保持内流速度在一定的范围内变动(3～6 m/s)，这对于提高整个扬矿子系统的稳定性、可靠性以及保证矿浆的输运效率等都是很重要的。

(2)随着内部矿浆密度的增大，输流软管的最大横向位移减小、最大主应力增大。为了避免由于矿浆密度变化范围太大引起输流软管位移和应力的大范围变化，应综合考虑集矿车性能等因素，保证输送矿浆的密度有一个相对稳定的变化范围。

(3)随着海流速度的增大，输流软管的最大主应力和最大横向位移都增大，当海流速度大于0.3 m/s时，靠近中间仓端输流软管的构形变化明显，与中间仓连接处出现折弯。为了保证在工程应用中输流软管有相对稳定的构形，输流软管更适合在海流速度小于0.3 m/s的海洋环境中工作。