不同截止高度角GPS/BDS组合伪距差分定位性能分析

贾 雪，徐 炜

(安徽理工大学 测绘学院，安徽 淮南 232001)

我国正在实施、自主研发、独立运行的北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)已经成为继美国的全球定位系统(Global Positioning System，GPS)、俄罗斯的全球定位系统(Global navigation System，GLONASS)之后，国际上第三个可以提供定位服务的导航系统。2012年底，BDS系统已实现对亚太周边提供导航定位服务，并按照BDS“三步走”的发展战略，计划2018年面向“一带一路”沿线及周边国家提供基本服务，2020年完成35颗卫星发射组网，为全球用户提供服务[1-2]。

高精度的定位主要使用载波观测值进行解算，但需要解算整周模糊度，且观测值容易出现周跳等因素的影响，在对于定位精度要求不高、提高定位速度的情况下，伪距差分定位已可以满足定位精度的要求[3]。在差分定位时，由于受到建筑物或树木的遮挡，导致单系统定位时的可见卫星数大大减少，共视卫星数少于4颗时将无法获得可靠的定位结果。而相对单系统而言，多系统融合定位具有较多的优势，可以增加共视可见卫星的数目，改善卫星空间分布的几何结构，提高定位的精度、可靠性和效率。国内外众多学者对GPS，BDS及其组合系统伪距定位进行了研究，唐卫明等[4]基于实测数据对GPS，BDS，GPS/BDS在不同遮挡下的可见卫星数、PDOP值及导航定位的可用性进行了研究；李鹤峰等[5]给出了了伪距单点定位的流程并利用实测数据验证了组合导航定位算法的正确性；王趁香等[6]基于辽宁连续运行参考站实测数据进行了GPS，BDS及其组合系统的伪距单差与伪距双差实验，证明双系统定位的优势。

本文考虑在建筑物及树木等信号易遮挡区域，GPS与BDS单系统可见卫星个数较少，无法达到相对定位的最低要求的问题，讨论GPS/BDS组合伪距差分定位解算模型。利用香港CORS站实测数据，在截止高度角为10°、20°、30°、40°的情况下，进行GPS，BDS，GPS/BDS 3种模式伪距差分定位解算，并对其定位精度进行比较分析。

1 GPS、BDS伪距差分定位模型

1.1 时间系统与坐标系统的统一

GPS采用GPS时(GPS time，GPST)和WGS84坐标系(World Geodetic System 1984，WGS84)，而BDS采用BDS时(BDS time，BDST)和CGCS 2000大地坐标系(China Geodetic Coordinate System 2000，CGCS2000)，GPS与BDS的时间基准与坐标基础都存在差异，因此在进行组合定位时需要将两者的时间系统与坐标系统进行转换和统一[7-8]。

BDS与GPS系统均采用原子时，秒长的定义相同，也都采用周和周内秒数进行计数，不同在于GPST的起始时间是1980-01-06的00:00:00的协调世界时(Coordinated Universal Time，UTC)，而BDST的起始时间是2006-01-01的00：00：00的UTC，GPS、BDS时间系统关系如图1所示[12-14]。

GPST与BDST的转换关系可表示为

BDT周数=GPST周数+1356，

BDT周内秒数=GPST周内秒数+14.

但在GPST周内秒数+14大于604 800时需要将BDT周数加1。

WGS84坐标系与CGCS2000坐标系所定义的大地原点、尺度、定向是相同的，参考椭球面参数也较为相近，唯有扁率有微小的差异。WGS84坐标系经过优化后的精度可达到2 cm，与ITRF2000精度基本一致，而CGCS2000与ITRF2000的差异大约在5 cm，所以，WGS84与CGCS2000存在cm级别的差异，在进行非精密测量时可将两坐标系间的差异忽略不计，对于伪距差分定位而言，其定位精度在m级-dm级，因此无需进行坐标系统的转换，直接将其视为统一坐标系统使用即可[9-10]。

1.2 伪距差分定位模型

GPS,BDS的伪距观测方程可以统一表示为[3,8]

(1)

(2)

设测站A，B在s时刻的观测方程分别为

(3)

上式相减，可以消除卫星钟差的影响，在基线距离较短时，由于电离层与对流层的相关性较强，也可以认为得到了消除，故可以得到

c·(δtA-δtB).

(4)

同理，可得t时刻A，B两测站的单差观测方程，将s时刻与t时刻的单差方程相减可得双差方程为

(5)

若A为基准站，则其坐标改正数为0，式(5)可以表示为

(6)

此时，未知参数有dxB，dyB，dzB，通过平差就可以计算出待定点B的坐标。

2 实验数据处理与分析

本实验采用香港CORS站的实测数据，分别采用HKSS-HKST、HKNP-HKST站点的两条基线进行GPS/BDS伪距差分解算，采样间隔均为30s。其中，HKSS-HKST基线长9.6 km，选取2017-08-18 00:00:00—23:59:59观测数据，共计2 880个历元；HKNP-HKST基线长34.0 km，选取2017-08-18 00:00:00—23:59:59观测数据，共计2 880个历元；通过不同截止高度角模拟不同遮挡环境，截止高度角分别设置为10°、20°、30°、40°。

2.1 不同截止高度角可见卫星数分析

分别对GPS,BDS,GPS/BDS系统进行伪距差分定位，设置卫星截止高度角为10°、20°、30°、40°，对比各定位系统的可见卫星数，并将计算结果与参考值作差，得出E,N,U方向的偏差及其RMS值。

在观测时段内，GPS,BDS卫星星空图如图2所示，GPS,BDS,GPS/BDS组合3种定位模式下9.6 km、34.0 km基线的可见卫星不同高度角可见卫星数时空分布百分比与区间分布统计如图3、表1所示。

图2 GPS,BDS卫星星空图

图3 GPS,BDS,GPS/BDS不同高度角可见卫星数时空百分比9.6 km基线34.0 km基线

表1 可见卫星数区间分布统计表%

由图3、表1可知，共视可见卫星数随着卫星高度角的增大而减少，在截止高度角为10°、20°、30°、40°时，9.6 km基线GPS单系统共视可视卫星数分别在8～9、6～8、4～5、<4～4颗左右，BDS单系统可见卫星数分别在8～9、7～9、6～7、5～6颗左右，GPS/BDS组合系统可见卫星数分别在17～19、15～17、12～14、9～11颗左右；34.0 km基线GPS单系统可见卫星数分别9～10、8～10、7～8、6～7颗左右，BDS单系统可见卫星数分别在8～10、6～8、5～6、4～6颗左右，GPS/BDS组合系统可见卫星数目数要分别在18～19、16、12～13、9～10颗左右；截止高度角从20°上升至30°时，9.6 km基线GPS可见4颗及以上卫星下降了8.13%，34.0 km基线GPS可见4颗及以上卫星下降了0.18%，截止高度角从30°上升至40°时，9.6 km基线GPS可见4颗及以上卫星下降了51.25%，34.0 km基线GPS可见4颗及以上卫星下降了0.87%，两条基线BDS,GPS/BDS可见5颗及以上卫星均达到了100%，组合系统的可见卫星数始终多于单系统的可见卫星数，两条基线在截止高度角为40°时的可见卫星数仍多于截止高度角为15°时GPS,BDS单系统的可见卫星数，可见GPS/BDS系统的卫星可见性和系统稳定性要强于GPS系统。

2.2 定位精度分析

本文在进行精度分析时，将9.6 km与34.0 km基线观测时段内的计算结果与参考值作差，得出两条基线GPS单系统、BDS单系统、GPS/BDS组合系统在不同截至高度角下E,N,U方向的基线偏差结果如图4、图5所示。

在6.9 km基线中，截止高度角为10°时，GPS单系统在E,N,U方向的平均偏差为0.173 m、0.087 m、0.271 m，BDS单系统在E,N,U方向的平均偏差为0.132 m、0.131 m、0.298 m，GPS/BDS组合系统在E,N,U方向的平均偏差为0.096 m、0.076 m、0.188 m，可见在GPS/BDS组合系统在E,N,U方向的定位精度均优于GPS、BDS单系统；截止高度角为20°时，GPS单系统在E,N,U方向的平均偏差为0.176 m、0.087 m、0.292 m，BDS单系统在E,N,U方向的平均偏差为0.178 m、0.157 m、0.469 m，GPS/BDS组合系统在E,N,U方向的平均偏差为0.103 m、0.079 m、0.221 m。在E方向，GPS系统与BDS系统定位精度相当，在N,U方向，GPS系统与GPS/BDS组合系统定位精度一致，而BDS系统在U方向的定位精度最差；截止高度角为30°时，GPS单系统在E,N,U方向的平均偏差为0.182 m、0.129 m、0.469 m，BDS单系统在E,N,U方向的平均偏差为0.229 m、0.243 m、0.858 m，GPS/BDS组合系统在E,N,U方向的平均偏差为0.117 m、0.103 m、0.334 m。GPS/BDS组合系统与GPS系统在E，N方向的定位精度基本相同，BDS在E,N,U方向的定位偏差最大，在U方向,GPS/BDS组合系统的定位精度明显高于单系统；截止高度角为40°时，GPS单系统在E,N,U方向的平均偏差为0.229 m、0.243 m、0.858 m，BDS单系统在E,N,U方向的平均偏差为0.247 m、0.236 m、1.229 m，GPS/BDS组合系统在E,N,U方向的平均偏差为0.135 m、0.130 m、0.646 m，GPS系统于BDS系统在E,N方向的偏差基本相同，但BDS系统在U方向的偏差大于m级，GPS/BDS组合系统的定位精度均优于m级。

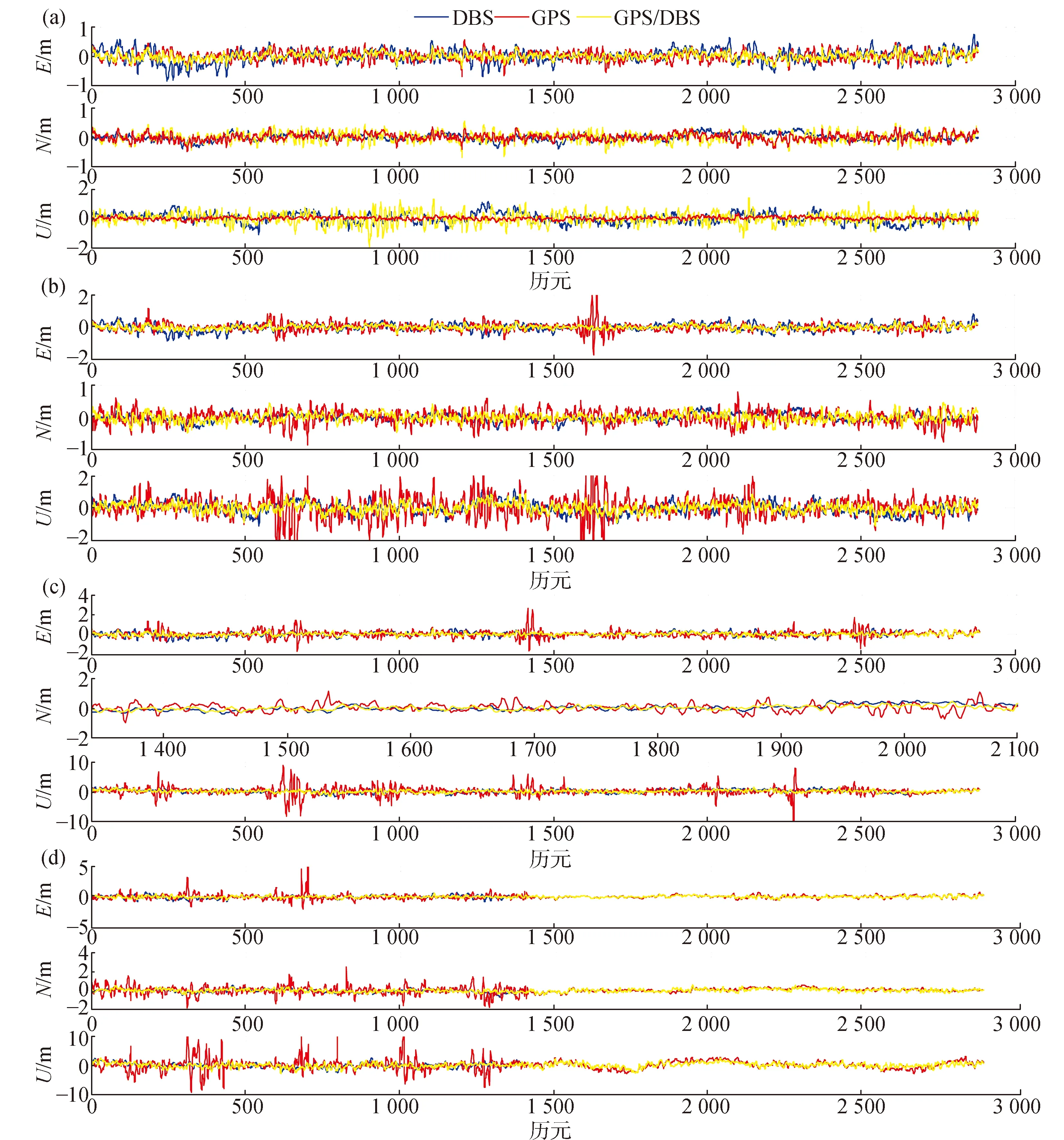
图4 6.9 km基线不同截至高度角E，N，U方向的偏差

在34.0 km基线中，截止高度角为10°时，GPS单系统在E，N，U方向的平均偏差为0.255 m、0.128 m、0.428 m，BDS单系统在E，N，U方向的平均偏差为0.163 m、0.160 m、0.375 m，GPS/BDS组合系统在E，N，U方向的平均偏差为0.144 m、0.094 m、0.244 m，可见在GPS/BDS组合系统在E，N，U方向的定位精度均优于单系统；截止高度角为20°时，GPS单系统在E，N，U方向的平均偏差为0.258 m、0.128 m、0.470 m，BDS单系统在E，N，U方向的平均偏差为0.219 m、0.188 m、0.592 m，GPS/BDS组合系统在E，N，U方向的平均偏差为0.155 m、0.098 m、0.305 m。在E，N方向，GPS、BDS的定位精度基本一致，在U方向，GPS系统优于BDS系统。截止高度角为30°时，GPS单系统在E，N，U方向的平均偏差为0.284 m、0.176 m、0.746 m，BDS单系统在E，N，U方向的平均偏差为0.276 m、0.277 m、1.033 m，GPS/BDS组合系统在E，N，U方向的平均偏差为0.171 m、0.138 m、0.481 m，在E方向，GPS,BDS,GPS/BDS系统的定位精度基本相同，在N方向，GPS,GPS/BDS系统定位精度相当，均优于BDS系统，在U方向，GPS系统的偏差起伏较大，可能是由于可见卫星数较少，定位精度较差，而BDS,GPS/BDS组合系统的偏差起伏变化较小；截止高度角为40°时，GPS单系统在E，N，U方向的平均偏差为0.322 m、0.233 m、1.594 m，BDS单系统在E，N，U方向的平均偏差为0.353 m、0.315 m、1.859 m，GPS/BDS组合系统在E，N，U方向的平均偏差为0.198 m、0.176 m、0.866 m，GPS/BDS组合的定位精度较好，在E，N方向均优于0.2 m，U方向优于1.0 m，相比单系统的定位精度提升的较为明显。

对不同截止卫星高度角下GPS单系统、BDS单系统、GPS/BDS组合系统在E，N，U方向偏差的RMS值进行统计，如表2所示。

图5 34.0 km基线不同截至高度角E，N，U方向的偏差

表2 伪距差分定位的RMS值m

续表2 m

由表2可知，在6.9 km基线中，截止高度角为10°、20°、30°时，GPS，BDS，GPS/BDS系统在E，N方向的定位精度均可达分米级，截止高度角为30°时GPS系统在U方向的偏差约1.35m，在卫星高度角为40°的极端条件下，GPS/BDS在E，N方向上可达到0.2 m之内，在U方向优于米级，定位精度优于GPS和BDS单系统；在34.0 km基线中，截止高度角为10°时，GPS与BDS的定位精度相当，截止高度角为20°、30°和40°时，BDS的定位精度仅次于GPS/BDS而优于GPS，这主要是因为BDS在随着高度角变化时，可见卫星数保持稳定，且有较高的卫星高度角，使其噪声较小，截止高度角为40°时，BDS和GPS/BDS在E，N方向上均可达到20 cm左右，U方向可达到1.1 m左右，GPS和BDS定位精度均低于GPS/BDS。两基线E，N，U方向偏差的RMS值随着卫星高度角的增加而逐渐增加，GPS/BDS组合定位精度最高，BDS定位精度略高于GPS系统，随着基线的增长，电离层与对流层延迟的相关性逐渐减弱，差分难以对其进行消除，故与34.0 km基线相比，6.9 km基线具有更高的定位精度。

3 结束语

通过设置不同截止卫星高度角，模拟出多种环境下GPS，BDS，GPS/BDS组合的伪距差分定位，并对各种模式下的可见卫星数、定位精度等方面进行对比分析，得出以下结论：

1)在不同的截止高度角下，伴随着基线的增长，电离层与对流层延迟的相关性逐渐减弱，差分难以对其进行消除，故与34.0 km基线相比，6.9 km基线伪距差分定位具有更高的定位精度；

2)GPS/BDS组合系统伪距差分定位精度均高于GPS、BDS单系统，多系统的融合增加可见卫星数，使得卫星的空间几何构型得到增强，同时提高系统稳定性；

3)随着截止高度角的增加，GPS,BDS和GPS/BDS组合系统的定位精度都呈出下降趋势，在高度角为10°、20°、30°、40°的条件下，E，N方向的定位精度均优于U方向定位精度，GPS/BDS组合系统的定位精度优于GPS,BDS单系统，在截止卫星高度角为40°的极端条件下，两条基线GPS/BDS组合伪距差分定位精度仍能达到米级左右。

[1] 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.

[2] 杨元喜,李金龙,徐君毅,等.中国北斗卫星导航系统对全球PNT用户的贡献[J].科学通报,2011,56(21):1734-1740.

[3] 戴伟,李明峰,吴继忠.北斗卫星导航系统伪距差分定位技术研究[J].全球定位系统,2015,40(2):36-39.

[4] 唐卫明,徐坤,金蕾,等.北斗/GPS组合伪距单点定位性能分析[J].测绘科学,2014,39(6):18-21.

[5] 李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS多模融合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.

[6] 王趁香.GPS、BDS与GPS/BDS伪距单点定位与差分定位精度分析[J].导航定位学报,2017,5(3):84-89.

[7] 严丽,李萌.BDS+GPS相对定位精度因子分析[J]. 测绘学报,2017,46(3):325-331.

[8] 李博,徐爱功,祝会忠,等.不同截止高度角BDS/GPS伪距单点定位性能分析[J].测绘科学,2016,41(12):32-38.

[9] PETER J, DENNIS G T, HHANG O B, et al. Contribution of the COMPASS satellite navigation system of the PNT users[J]. Journal of Aeronautics, Astronautics and Aviation, Series A,2013,42(4):223-230.

[10] 陶庭叶,王志平,蒋俊儒. GPS/BDS单历元基线解算中随机模型的确定[J].大地测量与地球动力学,2015,35(4):649-652.