利用Excel编制现场动平衡模型在实际中的应用

田 嘉

(本钢板材股份有限公司发电厂，辽宁本溪117021)

前言

振动水平是评价透平设备运行状况、安全可靠性最重要的标志之一。它是透平设备各部件在诸方面运行情况的集中反映。剧烈的振动将使零部件承受过高的动应力，使紧固部件松弛，滑动部件磨损或小间隙装配的动静部件发生摩擦，导致零部件疲劳损坏，一些重大的事故直接或间接与振动有关。振动问题是透平设备经常发生且比较难于处理的一类故障，而根据大量研究表明，大约一半左右的透平设备振动是由不平衡引起的。而快速解决由不平衡引起的振动解决方法是现场动平衡法。

目前现场动平衡的方法有采用动平衡仪和手动绘图两种方法。前者精确度高，通过试转、试加配重、再试转，即两次试转和一次试加配重就可确定不平衡量的相位和配重质量，但有一定不足之处，动平衡仪价格较为昂贵，并且需要精确测量转子键相，并不是每个使用透平机械设备的生产现场都能满足条件。手动绘图法虽然试转的次数较多，但不需测量转子键相，通过手动绘图即可准确计算出最终加重质量和角度，且一般平衡后的精度可以满足实际生产需要，也不需使用先进仪器，是透平设备现场找动平衡简单易行的可靠方法。本文讨论的是透过手动绘图法的理论本质，通过Excel编制现场动平衡模型，无需绘图就可以快速准确的计算出动平衡结果的一种方法。

1 现场动平衡理论基础

1.1 适用条件

平衡是指调整转子的质量分布，将不平衡引起的振动或轴承动反力减小到允许的范围内。在透平设备本体上进行的平衡过程称为现场动平衡。平衡的前提条件是转子系统是线性的，即转子产生的振动是基频；振幅与不平衡的大小成正比。绝大多数情况下，透平转子系统可以近似看作是线性系统。需要说明的是透平设备出现振动可能是除了平衡问题外同时存在其他故障，例如轴承工作条件恶化；动静部分摩擦；轴承座刚度降低；热膨胀不好等因素，一般的原则是首先消除不平衡问题，因为通过平衡可以有效降低振动基数，提高安全裕度；现场平衡实施比较简单，工作量小，通过平衡尽可能降低其他因素扰动力，使振动减小，因此即使存在平衡之外的故障，只要可以通过平衡使振动得到改善，就应该首先选择现场动平衡。

1.2 图解法原理

透平设备现场动平衡采用动平衡仪由内部计算机完成运算，其理论方法是图解法。计算原理是首先测量机组的原始振动A的振幅和相位，后在转子上安装一个试加配重T，并测量试加配重后振动B的振幅相位，依照试加前后的振幅和相位变化可以计算出最终加重质量的大小和角度。

如图1所示，首先在极坐标上画出矢量A和矢量B，A为原始不平衡产生的振动，B是原始不平衡和试加配重共同作用产生的振动，则由试加配重引起的振动为：

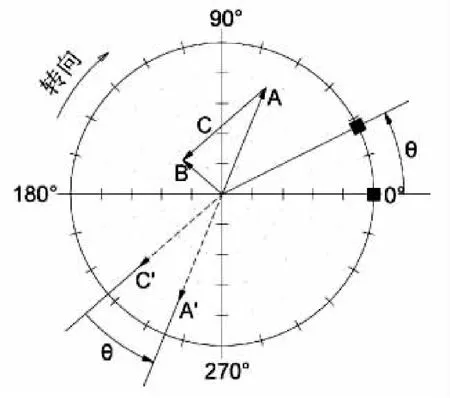
图1 图解法原理

由矢量三角形法则，在极坐标上得到矢量C，为了方便分析，将矢量C的起点移至坐标原点，即C’。为了实现转子的完全平衡(即振幅为0)，由试加配重产生的矢量振动 (假定试加配重安装在0°位置)，应该与A大小相等，方向相反，即A’。根据转子振动响应的线性关系，振幅与不平衡量成正比，最终加重W的大小确定为：

而C需要逆时针旋转θ才能够与A’重合，所以试加配重应以0°为基准逆时针旋转角度θ得到最终加重位置。

1.2 等分三点平衡绘图法

上述采用的图解法需要同时测得振动的大小和相位，才能计算最终加重质量和角度。而等分三点平衡绘图法则只需要测出三次试加配重后的振动值，减少了相位测量环节，即只依靠简单的振动表即可进行绘图计算。其具体绘图过程如下：

①首先在预平衡的转子圆周按相互间隔120°标记出三个基准点(即试加配重点)，分别为X、Y、Z。

②将称量好的试加配重首先加在X点上，启动设备达到额定转速，稳定后测得的振动值为a(振动值单位均为μm)，该数值可以选取轴振也可选瓦振，需根据透平设备具体情况确定(若取瓦振，一般来说取垂直、轴向、或水平方向振动数值最大者)。

③依上述方法将试加配重移至Y点测得的振动值为b，试加配重移至Z点测得的振动值为c。将三次试转的振动值做好记录，准备绘图计算。

④首先根据三次测得的振动值a、b、c为半径画三个同心圆弧，圆心为O(圆弧的半径值与振动数值按照比例绘制，需要说明的是：本文是按照振动数值a＞b＞c作为例子，实际应用中无论何种大小排列关系，只要掌握相互对应关系即可)。

⑤在大圆任取一点N，以此为圆心，以a为半径画弧交大圆弧于点A；再以N为圆心，以c为半径画弧交中圆弧于点B；以B为圆心，以AB的长度为半径画弧交小圆弧于点C。

⑥连接AB、BC、CA形成△ABC，则△ABC为正三角形(证明过程不再赘述)，做△ABC的外接圆，得圆心O’，连接OO’交△ABC的外接圆于点M。

⑦绘制出的图形如图2所示 (点N未绘制)，则点M为实际加重点。点M位于B、C之间，具体加重位置根据∠CO’M或∠BO’M的角度确定。加重质量可以根据试加配重质量和OO’、OM长度得到，加重质量=试加配重质量×(OO’/OM)。

说明：基准点(试加配重点)X、Y、Z 与 A、B、C 三点的对应关系为：X对应A点；Y对应B点；Z对应C点。实际加重点M位于两次振动较小的B、C点之间，根据基本常识可以得出规律：实际加重点总是位于两次振动较小的试加配重点之间，在实际应用中这是一个防止试加配重点与振动值对应关系搞错的一个诀窍。

图2 等分三点绘图法原理

2 基于Excel现场动平衡模型编制

该模型编制的基础为向量计算，即将振动的大小和相位编制向量方程求解最终加重质量和角度。

2.1 等分三点法推导

设三次试加配重基准点分别为X、Y、Z(三点按逆时针顺序排列)，三点对应的位置互相间隔120°，设试加配重质量为g，产生的振幅为M，另设试加配重在X位置产生振动的相位角为0°，则逆时针旋转120°得到Y位置产生振动的相位角，同理Z位置振动产生的相位角由X位置产生振动的相位角逆时针旋转240°得到。则试加配重在X、Y、Z三点上产生的振动对应向量分别为：

设转子原始不平衡向量为K，产生的振幅为N，相位角为α，则不平衡向量K为：

K=Ncosα+iNsinα

其中α为转子原始不平衡向量与向量A逆时针方向的夹角。则X、Y、Z三点加重后与转子原始不平衡向量叠加后的向量分别为A、B、C：

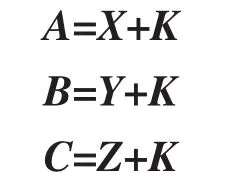
根据A、B、C的模列方程：

将方程展开整理得：

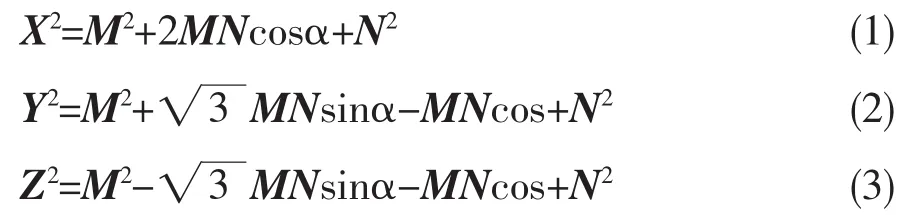
由(1)+(2)+(3)得：

由(2)-(3)并与(1)联立得：

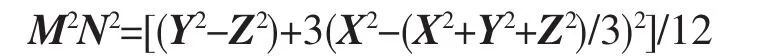
分别设 S、T：

解方程得：

解1：

解2：

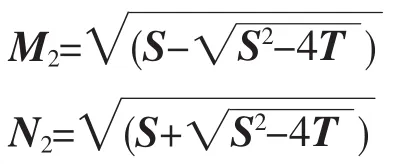
注：解1为试加配重不平衡M大于转子原始不平衡N，解2为试加配重不平衡M小于转子原始不平衡N。正常来说试加配重较小，导致的不平衡振幅M一般小于转子原始不平衡振幅N，因此一般把解2当做实际解，当然也不排除存在解1的情况，所以在找动平衡之前确定试加配重的大小是十分重要的。

最后根据求得的M、N计算出cosα、sinα的数值，得到α的角度值。

根据以上推导，求得最终加重的质量G=gN/M，加重的角度为α旋转180°后得到的β。

2.2 基于Excel模型的编制

根据等分三点法的公式推导可见，计算的过程较为复杂，工作量较大，而若采用Excel作为模型编制计算公式，可使最终结果快速准确的得到，十分方便快捷。图3为依据等分三点法原理采用Excel编制的动平衡计算模型。

图3 等分三点法计算模型

图3 表格中的数值为模拟计算值。

编制该模型的要点：

①要掌握好相位角的旋转方向，切记所有的相对角度关系都是由X点产生振动的相位角0°逆时针旋转得到的。

②α角度值不能单凭sinα或cosα的值确定，要根据sinα和cosα的正负关系确定。

2.3 通用三点法推导及模型编制

采用等分三点法可以应用于大部分实际问题，但由于个别设备存在试加配重的三等分点被平衡块所占据，或根本无法将试加配重放置在三等分点的情况，那么等分三点法将失去作用，所以根据实际需要，必须采用通用三点法予以解决，通用三点法即三点试加配重的位置可以选取任意角度。通用三点法的计算推导过程：

首先基本假设和符号与等分三点法一致，但有所不同的是：Y位置产生振动的相位角是由X位置产生振动的相位角逆时针旋转θ得到，则Z位置是逆时针旋转φ得到。试加配重在X、Y、Z三点上产生的振动对应向量分别为：

转子原始不平衡向量为：

则有：

则根据A、B、C的模列方程：

将方程展开整理，并设：

则可得：

则根据方程推出：

以上方程实际推导过程不再详细论述。与等分三点法同理解得：

求得α的角度、β的角度以及加重质量G与等分三点法相同。图4为依据上述推导公式采用Excel编制的通用三点法动平衡计算模型。

图4 通用三点法计算模型

图4 表格中的数值为模拟计算值。

编制该模型的要点：①与等分三点法类似，要掌握好相位角旋转方向和参照以及根据sinα和cosα的正负关系确定α值。②该模型中间变量较多，编制公式时不要弄错。

2.4 加重的分解

在最终算得的加重质量和角度后，即可将称量好的配重加在计算位置，但特殊情况时该位置已有平衡块或不具备加重条件，此时需要将该加重质量分解到两侧某两个位置，它们共同作用产生的效果等同于配重在计算位置产生的加重效果。

设在计算位置加重质量为g，左侧与计算位置之间夹角为θ，加重质量为g1，右侧与计算位置之间夹角为 φ，加重质量为 g2。其中 g、θ、φ 为已知，g1、g2为未知。则根据三角函数关系，可得(推导过程不再详述)：

3 动平衡模型的实际应用

某台汽轮鼓风机在运行中发现3瓦轴振超标，振动值0.071 mm，经检修人员多次检查未发现异常。初步判断是动平衡不好导致振动超标，拟采用等分三点法找现场动平衡，但整个转子只有在联轴器开有8个配重孔，每两孔之间的角度差为45°，无法采用等分三点法，遂采用通用三点法找动平衡。三次试加配重位置的相位为 0°、135°、225°，配重质量为20 g。

经过3次试转，得出三次振动值，通过Excel编制动平衡模型的计算，最终加重质量为试加配重质量的 1.67 倍，即 33.4 g，角度为-54°。因在-54°位置处无法加重，需在两侧平衡孔加重，通过加重分解得出：在-45°位置加重 1.39 倍，即 27.8 g；在-90°位置加重0.37倍，即7.4 g。加重试转后该位置振动值下降到0.034 mm，满足该机组运行要求。

详细数据见表1。

表1 平衡前后各瓦振动值

4 结论

透平设备现场动平衡采用Excel编制的等分三点法、通用三点法模型可快速准确的计算最终加重质量和角度，并在实际应用中取得满意的平衡效果。另外该Excel模型根据动平衡理论，还可编制90°及180°两点法。

总体来说，该Excel模型运用起来较为灵活便捷，为技术人员解决透平设备不平衡引起的振动问题提供良好的技术支持。