进口工业应用弛张筛结构分析
2018-07-20段旭升张俊山雷晓树
段旭升,张俊山,雷晓树,李 旭
(1.河南中平鲁阳煤电有限公司,河南 平顶山467312;2. 神华准格尔能源有限责任公司选煤厂, 内蒙古 鄂尔多斯010300;3. 平顶山天安煤业股份有限公司 田庄选煤厂,河南 平顶山467013)
在我国选煤厂原煤筛分阶段,潮湿原煤深度筛分(<13 mm粒级的干法筛分)是当今筛分技术中亟需解决的难题。煤炭在进行深度筛分时,由于潮湿细粒煤粘性较大,极易粘附在筛板上造成堵孔,或是粘附在大颗粒上成为筛上物[1-2]。普通振动筛的筛板随筛机同步运动,弛张筛采用柔性筛面对物料进行筛分,改变了筛面在筛机上的运动方式,可彻底解决煤炭深度筛分的堵孔问题[3]。
由于我国装备制造业水平的限制,目前在工业应用中较为成熟的弛张筛大多为进口设备,笔者结合其中两种弛张筛的结构特点对其进行结构分析。
1 弛张筛工作原理
驰张筛筛分原理如图1所示,l为弛张筛筛板,O1和O2为弛张筛筛梁,w为筛板最大挠度,筛板由柔性聚氨酯材料制造,在筛分过程中筛板可发生变形,筛梁O1和O2的间距也可变化。在筛分过程中,O1、O2的间距在物料运动方向上(x方向)循环变化,从而带动筛板做弛张运动。在弛张运动过程中筛面上的筛孔略微变形,可使卡在筛孔中的煤炭颗粒穿过筛面进入筛下物,或是由于筛面较大的弹性被弹离筛面;当筛面达到平衡位置时,在垂直于x方向的速度达到最大,筛面对物料的抛射强度也达到最大,此时粘附在筛面的粘性细小颗粒被揉碎并弹离筛面[4],因此,弛张筛可解决潮湿细粒煤筛分过程中的堵孔现象。
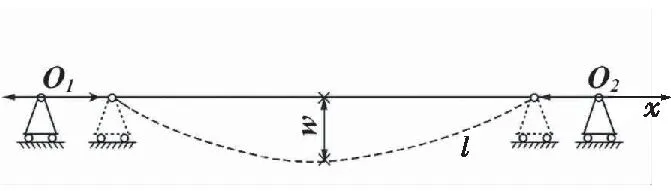
图1 弛张筛结构筛分原理图
筛面达到平衡位置时,被筛颗粒受到的抛射强度可达50g[5],与普通振动筛相比(普通振动筛由于筛面为刚性,不可变形,物料所受到的抛射强度和筛机振动强度相等,一般为4~6g),物料所受到的抛射力显著提高,被筛颗粒在筛面上可弹升0.5 m甚至更高,因此可很大地提高物料在筛面上的运动速度和弛张筛的处理能力。同时,由于筛面在弛张过程中发生弯曲,筛面不同位置的相位和振幅各不相同,颗粒在脱离筛面时的速度和方向也各不相同,使被筛颗粒在空中产生激烈碰撞,粘附聚集的物料充分被打散,有利于物料的离析分层,为下一步的透筛过程做好准备。
根据驱动方式不同,我国选煤厂中应用的弛张筛主要有两种:一种是以海茵雷曼公司为代表生产的曲柄连杆驱动式的LIWELL弛张筛,另一种是以奥地利宾得公司为代表生产的激振器驱动式的宾得弛张筛。
2 LIWELL弛张筛
2.1 结构
LIWELL弛张筛主要由两个筛箱组成,结构如图2所示,内筛箱1通过橡胶弹簧4安装在筛机支架5上;外筛箱2通过导向弹簧3悬挂在内筛箱上。弛张筛工作时,驱动部分产生的力使两筛箱做相对运动,由于筛板两端分别固定在内外筛箱的横梁上,因此可以带动筛板做弛张运动[6]。
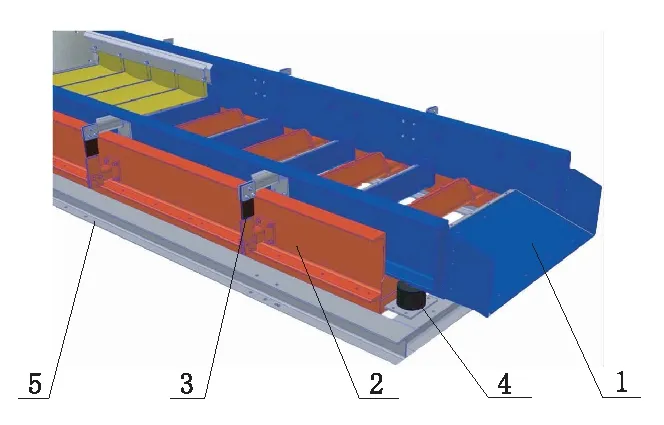
1—内筛箱;2—外筛箱;3—导向弹簧;4—橡胶弹簧;5—筛机支架
2.2 驱动原理
如图3所示,LIWELL弛张筛的驱动原理可简化为曲柄连杆机构,其中O点代表驱动轴(即内筛箱),固定在筛机支架上,偏心轴承中心A点与O点之间的偏心距构成曲柄。筛机工作过程中,曲柄OA沿驱动轴O以ω的角速度旋转,从而带动外筛箱与内筛箱做相互运动。
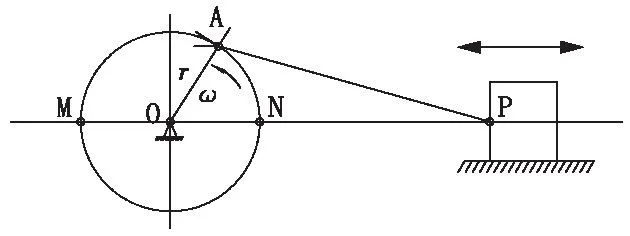
图3 LIWELL弛张筛曲柄连杆模型
连接内外筛框的推拉弹簧如图4所示,推拉弹簧可简化为连杆AP,在沿物料方向上(即OP方向)可将曲柄OA的驱动力传递至外筛框P;由于推拉弹簧自身特性,在物料垂直方向上可产生微小变形而不影响其他力学性能,曲柄OA传递到外筛框P的驱动力可忽略不计,因此LIWELL弛张筛内外筛框仅在沿物料方向上产生弛张运动。

图4 连接内外筛框的推拉弹簧
根据三角函数的关系,外筛框的速度为
v=ωrsinωt。
(1)
式中:v为外筛框的速度,m/s;r为偏心半径(即曲柄长度),m;ω为主轴角速度,rad/s;t表示开机时间(此处定义开机时曲柄OA从N点沿逆时针运动),s。
根据式(1)得到外筛框的运动速度曲线,如图5所示。
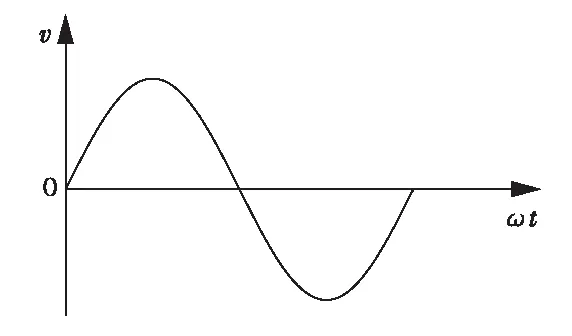
图5 外筛框的速度曲线
由图5可知,当曲柄OA达到平衡位置时(即与MN垂直的位置)外筛框的速度最大,此时其速度与偏心中心点A的线速度相等,都为ωr。曲柄到达M点和N点时外筛框速度为零,达到极限位置,因此MN即为该筛机的振幅。
3 宾得弛张筛
3.1 结构
宾得弛张筛由主筛框、浮动筛框、激振器、筛板、剪切弹簧与隔振弹簧等部件组成(图6),主筛框为宾得弛张筛的主要结构,通过减振弹簧安装在基础支架上;浮动筛框通过剪切弹簧安装在主筛框的下部;激振器安装在主筛框的中间;筛板两端分别安装在两筛框上[7]。筛机工作时,激振器产生激振力带动主筛框做圆振动,同时浮动筛框通过二次激振做椭圆运动,在物料运动方向上主筛框与浮动筛框的运动方向相反,从而带动筛板做弛张运动[8-9]。
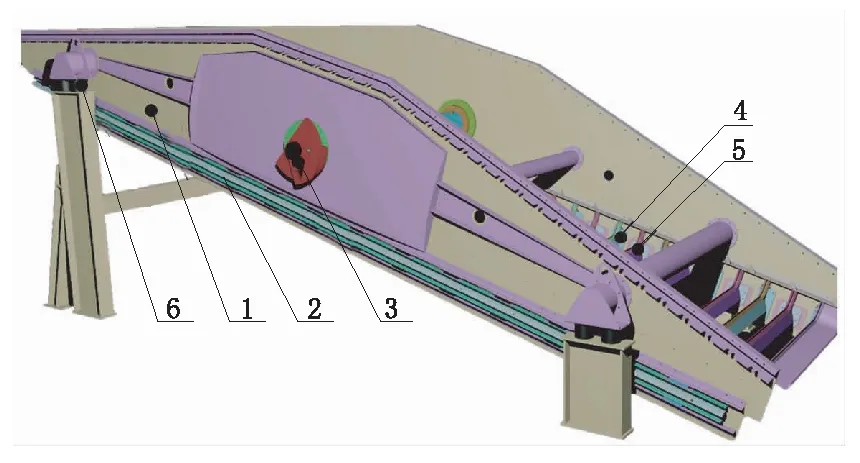
1—主筛框;2—浮动筛框;3—激振器;4—固定筛梁;5—浮动筛梁;6—隔振弹簧
3.2 振动机理
用质量集中法建立宾得弛张筛的力学模型,如图7所示,由于阻尼很小,此模型忽略了弛张筛运动过程中所受到的阻尼。m1为主筛框,通过橡胶弹簧k1与基础支架相连,并安装有激振器,在x方向上所产生的激振力为fcosωt(由激振器偏心块产生的激振力f在x轴的分量所得),m2为浮动筛框,通过剪切弹簧k2与主筛框相连[10-11]。

图7 宾得弛张筛力学模型
根据图7所示的力学模型,建立弛张筛的振动的微分方程为:
m11+(k1+k2)x1-k2k1=fcosωt
m22-k2x1+k2x2=0。
(2)
此方程式为二阶线性常系数非齐次微分方程组,它的解由齐次方程的通解和非齐次方程的特解叠加而成。齐次方程的通解对此问题无意义,特解为稳定阶段的等幅振动,可通过方程组的特解得到所需各参数的值。设方程组的特解为:
x1=A1cosωt
x2=A2cosωt,
(3)
式中:A1为主筛框的振幅,m;A2为浮动筛框的振幅,m。
设a=k1+k2m1,b=k2m1,c=fm1,d=k2m2。将a、b、c、d和式(3)分别代入式(1),可得方程组的解:
A1=c(d-ω2)(a-ω2)(d-ω2)-bd
A2=cd(a-ω2)(d-ω2)-bd。
(4)
当m1、m2、k1、k2和f值确定后,可得到振幅A1、A2随频率ω变化的幅频特性曲线,如图8所示。
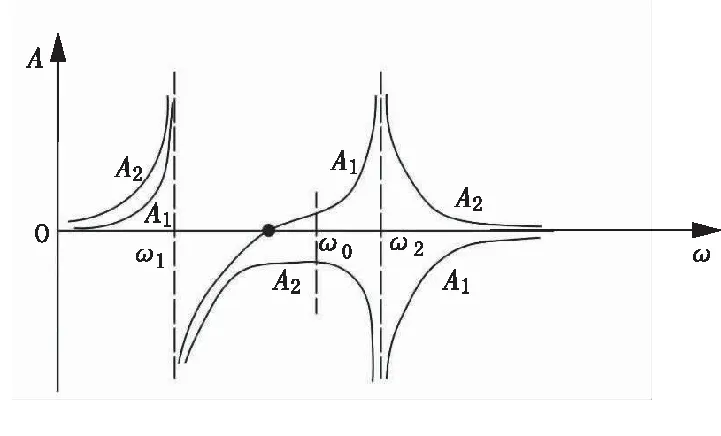
图8 宾得弛张筛幅频特性曲线
由图8可知,ω1和ω2为弛张筛振动系统的共振频率,当理论振动频率ω0接近这两点时,系统将产生共振。而当弛张筛的工作频率接近ω0时,m1、m2的振幅比较稳定,且主筛框和浮动筛框的振动方向始终相反,此时系统可以以较小的激振力获得较大的振幅,使弛张筛筛面产生较大的振动强度。
4 结论
(1)弛张筛采用柔性筛面对物料进行筛分,通过筛分过程中筛面及筛孔的微小变形,可彻底解决潮湿粘煤深度筛分容易堵孔的现象。
(2)LIWELL弛张筛基本原理可简化为曲柄连杆机构,外筛框的振幅和速度与曲柄的长度和转速相关;由宾得弛张筛幅频特性曲线可知,当工作频率接近ω0时,可以以较小的激振力使主筛框和浮动筛框得到较大的稳定振幅。
