直接示教机器人的位姿优化算法研究与实现*＊

凌冠耀 刘建群 高伟强

(广东工业大学机电工程学院，广东省微纳加工技术与装备重点实验室，广东广州510006)

示教再现是目前主流的工业机器人操作控制方式。常用的示教方法包括示教盒示教、操纵杆示教、主从机器人示教和直接示教等。与其它示教方法相比，直接示教机器人能以直接拖动方式实现复杂轨迹的示教，具有操作简单、示教方便等优点，在喷涂、弧焊、抛光等任务轨迹复杂的工业加工领域具有较高的应用价值。

对于直接示教机器人，示教过程中的人手抖动会直接反映到示教轨迹中，使机器人在再现过程中产生振动。限制了直接示教机器人在末端位姿要求较高的机器人表面加工领域中的应用，并降低了机器人的使用寿命和机械性能。因此，在最大限度地还原示教轨迹的同时减少再现过程中出现的振动对提高直接示教型机器人的适用性具有重要意义。

传统工业机器人的轨迹研究主要集中在机器人关节空间的轨迹规划［1］和以时间(能耗)为目标的轨迹优化问题［2－4］，但此类方法得到的末端轨迹难以满足喷涂、弧焊等直接示教机器人应用场景的精度要求。为了获得高精度的末端轨迹，文献［4］提出了基于NURBS样条的机器人笛卡尔空间轨迹规划方法，并对末端速度进行了控制，但该方法没有考虑任务轨迹中的姿态变化。文献［5］利用四元数圆弧函数实现了高精度的位姿轨迹规划，但该方法主要针对空间圆弧轨迹，无法直接适用于直接示教机器人的位姿平滑优化。

针对直接示教机器人的末端轨迹优化问题，提出了一种基于曲线拟合的位姿优化方法。分别利用B样条曲线和四元数曲线对直接示教轨迹进行拟合，给出了一种基于泰勒展开的四元数曲线插补方法，有效地还原了示教轨迹，减小了机器人末端的加速度波动，从而减小了直接示教机器人在再现过程中的振动。

1 轨迹预处理

在直接示教过程中，机器人控制器对各关节编码器进行高频采样获得的稠密示教轨迹数据存在大量冗余信息，为了提高优化处理效率，以时间间隔为α对示教轨迹进行重采样，得到的采样轨迹记为 M，轨迹中的位姿信息可以用机器人末端相对于基坐标系的齐次变换矩阵表示:

式中:Ri∈!3×3为第i个轨迹点相对于机器人基坐标系的旋转变换;Pi∈!3×1为第i个轨迹点的机器人末端坐标系相对于机器人基坐标系的平移变换。记机器人末端位置集合为旋转变换集合为

为了更好地对采样轨迹中的姿态信息进行处理，引入单位四元数对采样轨迹中的姿态信息进行描述。单位四元数具有以下形式:

式(2)可以表示为以θ为旋转角，n为旋转轴的三维空间旋转运动。

根据文献［6］，可以把旋转矩阵序列R转换为对应的单位四元数序列

2 位姿拟合

式中:di是B样条曲线控制顶点;Ni，3u()为定义在节点矢量U上的3次B样条基函数。Ni，k满足如下递推关系:

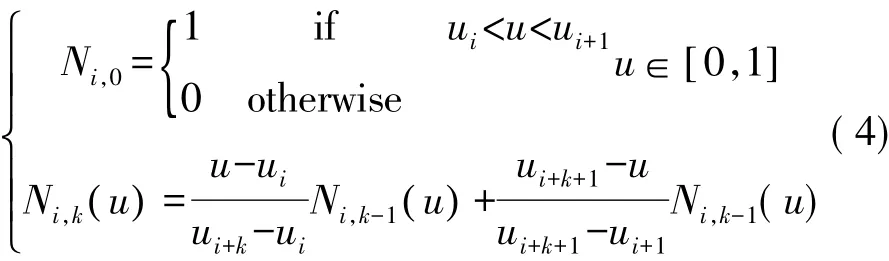
得到位置曲线后，考虑构造四元数曲线对示教轨迹中的姿态信息进行插值拟合。四元数对数运算定义为:

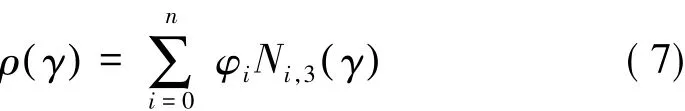
其中:φi为控制顶点;Ni，3(γ)为定义在节点矢量 Γ 上的3次B样条基函数。对序列ρ{ρi}ni=1进行弦长参数化获得节点矢量Γ后，控制顶点φi可以根据文献［8］进行求解。最后，利用指数映射，得到四元数曲线:

3 轨迹生成

为了获得离散的轨迹点序列，根据采样轨迹的时间位移关系，对拟合曲线进行插补。假设两个时间间隔为α的采样轨迹点的位置分别为P βi( )、P(βi+1)，由于插值曲线会经过所有的采样点，两个采样点间的轨迹位移为这两个采样点间的曲线段弧长，则P βi( )、P(βi+1)两点间的位移为:

上述积分可以通过常用的辛普森积分公式进行求解。记 P βi+1( )处的累计位移为Li=Li－1+ΔL，P βi+1( )在示教轨迹中对应的运动时间为Ti=Ti－1+α，以时间及对应的累计位移作为约束，利用三次样条插值［9］对位移进行插值，并根据时间分割法获得每个时间间隔对应的末端空间位移增量序列。姿态角位移增量序列的计算方法与之类似，在此不再赘述。

得到位移增量以后，采用泰勒展开法对位姿拟合曲线进行插补。参数τ在τ=τi处的一阶泰勒展开式为:

式中:ΔT为机器人运动插补周期，HOT为泰勒余项。

为了简化计算，采用一阶泰勒展开式进行插补。对于位置拟合曲线P(u)，在t=ti时刻瞬时速度可表示为:

把公式(11)代入公式(10)可得，机器人位置曲线的插补参数迭代式为:

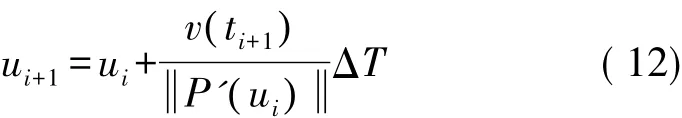
为了对机器人姿态曲线的运动速度进行控制，对位置轨迹的插补方法进行推广，给出了一种四元数曲线插补方法。假设四元数曲线角位移关于参数γ的函数为Θ(γ)，角速度关于时间t的函数为ω( t)，由复合函数求导法则可知:

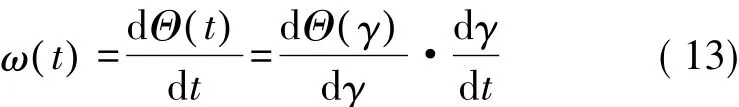
根据文献［10］，单位四元数曲线角速度关于参数γ的函数可以表示为:

把式(14)代入式(13)，得到的四元数曲线姿态瞬时角速度可以通过公式(15)表示:

令τ=γ，把式(15)代入式(10)，可得四元数曲线插补式为:

4 实验

以自行研制的六关节直接示教喷涂机器人为实验平台，对所研究的轨迹优化算法进行评估验证。机器人如图1所示。

以一个实际喷涂工序为例。在示教阶段，机器人以固定的时间间隔实时对各关节编码信息进行采样，通过所获示教关节角序列可以生成末端示教轨迹。截取该示教轨迹中一段总位移为3 222.237 mm的连续示教轨迹片段作为实验对象，经过算法处理得到优化轨迹。下面分别从轨迹误差和运动情况两个方面对上文提出的算法进行分析验证。

示教轨迹与优化轨迹的末端位置对比如图2。示教轨迹与优化轨迹末端姿态欧拉角对比如图3。其中，实线为示教轨迹，虚线为优化轨迹。从图2、图3中可以看出，经过优化处理后的机器人末端位姿优化轨迹与原示教轨迹基本保持一致。

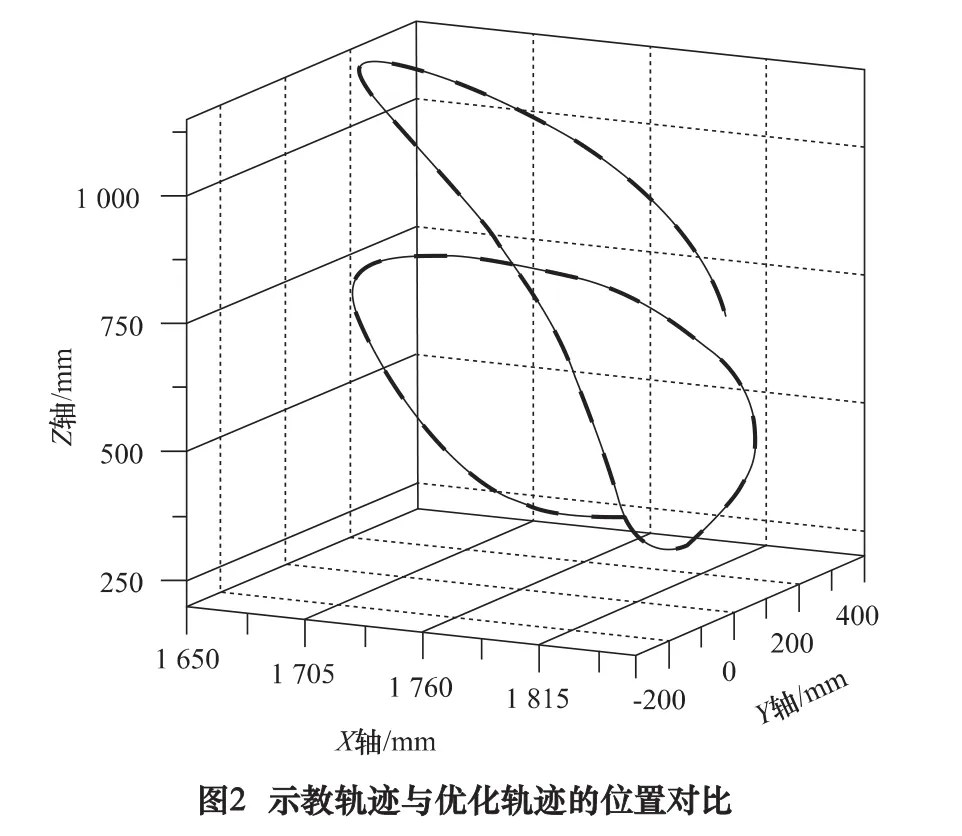
进一步对轨迹误差进行评价，以示教轨迹点Pi与优化轨迹点P'i之间的距离e作为位置误差进行计算:

机器人优化轨迹与示教轨迹末端位置误差分布如图4，欧拉角误差分布如图5。经过计算，优化轨迹最大位置误差为3.197 mm，平均轨迹误差为0.229 mm，标准差为0.468 mm。从图4的位置误差分布中可以看出，优化轨迹与示教轨迹整体误差较小，且在平均误差附近的分布较为集中，虽然个别轨迹点与示教轨迹存在较大的位置误差，但考虑到示教轨迹中可能存在孤立的噪声点，而且这些点在总体上占比较小，可以忽略其影响。

优化轨迹的欧拉角误差如表1所示。从表1可以看出优化轨迹的欧拉角误差较小，能够满足机器人实际使用要求。

表1 优化轨迹的欧拉角误差 rad

对上述结果进行综合分析，算法处理后的优化轨迹与原始示教轨迹间的误差较小，能够很好地对示教轨迹进行还原。

为了对算法的优化效果进行验证，分别对示教轨迹与优化轨迹的位姿速度、加速度曲线进行分析对比。机器人末端轨迹位置的速度、加速度对比如图6、图7所示，机器人末端姿态的速度、加速度对比如图8、图9所示，其中，虚线为示教轨迹，实线为优化轨迹。

可以直观地看出，经过优化处理后的机器人末端轨迹运动速度曲线具有更好的光顺性，并显著地减小了机器人末端位姿轨迹的加速度波动。将优化轨迹转换为关节角序列，在机器人上进行再现，实验结果显示，所提出的算法有效减小了再现过程中的振动。

5 结语

针对机器人直接示教轨迹平滑性差、加速度变化频繁导致机器人在再现过程中出现振动的问题，提出了基于曲线拟合的位姿优化算法。实验结果表明，该算法能在还原示教轨迹的同时有效减小机器人再现过程中的振动，对提高直接示教机器人在工业加工领域的适用性具有一定的实际应用价值。在进一步的研究中，将对拟合方法进行改进，实现对轨迹误差的控制。