一类遗传学问题的通解初探

江西

一、问题的提出

在高中生物的遗传学部分，孟德尔遗传规律是重点内容，其中将自由组合定律比例分解成若干个分离定律比例乘积的形式，是解决遗传学问题的基本思路。通常，分解过程需要依靠观察能力和经验来完成，这对解决较简单、常见的比例问题比较方便，但是遇到较陌生、复杂的比例问题，则无法依靠观察和经验解决。如一个遗传学问题得到的自由组合比例为315∶254∶7，此组数据较复杂，通过观察很难作出正确判断。下面笔者将对该课题的探索过程进行叙述。

二、初步尝试

由9∶3∶3∶1=（3∶1）2和6∶3∶2∶1=（2∶1）（3∶1）均存在相同的对应关系，联想到此对应关系类似于数学中的因式分解，随即构造以下二次多项式并完成因式分解：

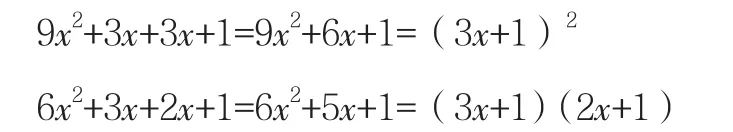
经整理分析发现数学中存在着相应的等式关系，可以大胆设想：对于遗传学中一个任意比例a∶b∶c∶d均可构造二次多项式ax2+bx+cx+d=ax2+(b+c)x+d，若令b+c=e，则ax2+bx+cx+d=ax2+ex+d;若能将ax2+ex+d因式分解成（mx+p）(nx+q)的形式，则有a∶b∶c∶d=（m∶p）（n∶q）。基于以上分析，笔者利用数学方法成功地将ax2+ex+d因式分解为（mx+p）(nx+q)的形式，因式分解过程如下：

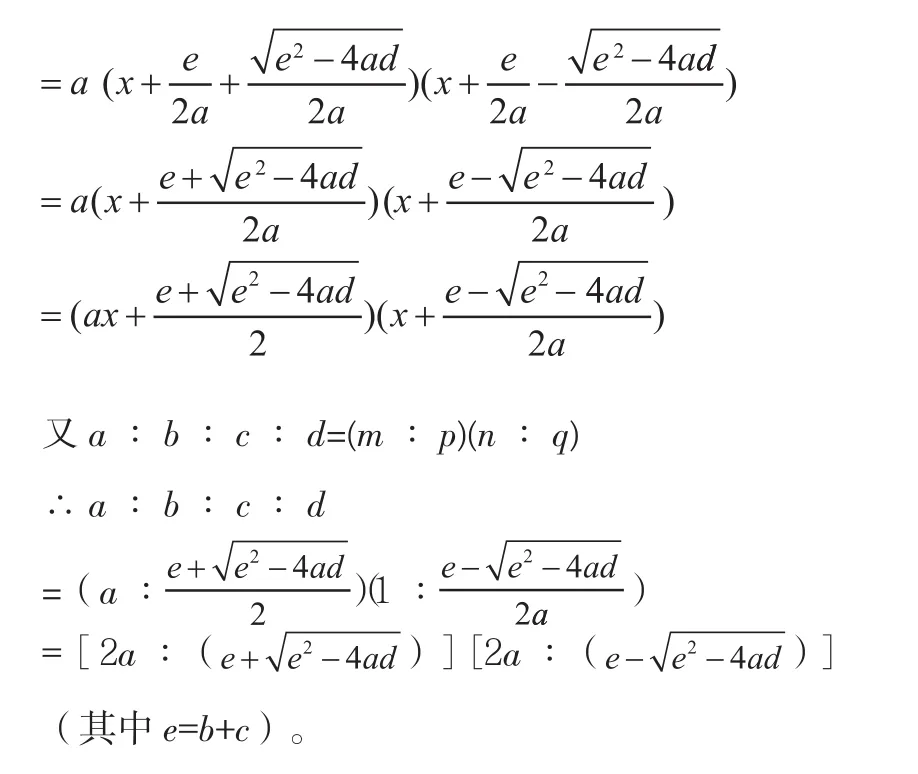
三、公式的验证

可以将以上实例代入公式中验证：

（1）若比例为9∶3∶3∶1，令a=9，b=c=3，d=1，则e=b+c=6，代入上述公式得（3∶1）2

（2）若比例为6∶3∶2∶1，令a=6，b=3，c=2，d=1，则e=b+c=5,代入上述公式得（2∶1）（3∶1）

由以上验证可知，上述公式成立。

四、用公式处理较复杂的比例问题举例

用公式法处理文章开头提出的问题，可快速得出结果：由自由组合比例为315∶254∶7知，a=315、e=254、d=7，借助公式推导为

315∶254∶7=（9∶7）（35∶1）

五、机械化处理该问题的设想

受吴文俊院士用数学机械化方法证明几何定理的思路的启发，对利用数学机械化方法处理上述问题作出以下设想：

第一步：给参数a、e、d赋值。

第二步：代入上述公式运算。

第三步：得出结果。

第四步：用数据库检索，得出亲本的基因型。