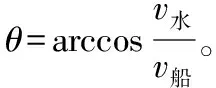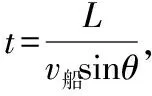活用矢量运算法则 解决小船渡河问题

河北 牛红标

高中物理中的小船渡河问题是运动的合成与分解知识中典型的应用实例，是学习复杂运动的基础，深刻理解合运动与分运动的等效性、等时性、分运动的独立性，灵活掌握相关的解题方法，学会运用正交分解的思想，对学习物理的思维培养是有极大帮助的。

一、首先阐述几个概念

1.航向：航向的英文单词是heading，这个词的词根是head，表示头部，和头有关的航向概念就是基于头而理解的。 对于船只、飞机或者其他交通工具，航向表示船头(或机头)所指的方向。

2.航线：又名航迹，英文用单词track表达，track在英文中指的是车辆在地面上行驶之后，轮子留下来的轨迹路线。 用在船只航行与航空上，道理也是一样的。 由此可见，航线是交通工具行驶在空间对应的真实轨迹。

3.合速度：物体实际运动的速度，可以是物体同时参与多个运动的结果。

对于小船渡河的问题，以地面为参考系，可以理解为它同时参与两个分运动,一是小船相对水的运动(设水不流时船的运动，即在静水中的运动)，二是随水流的运动(即水冲船的运动，等于水流的运动)，船的实际运动为合运动。

对于船在水中运动问题分为三种：顺水运动，船相对水的运动与水流速度方向相同，这时船对地的速度为两个速度相加；逆水运动，船相对水的运动与水流速度方向相反，这时船对地的速度为两个速度相减；渡河问题，船头与水流速度方向成某一角度，从河的一岸到对岸。本文只讨论有关船只的渡河问题，渡河问题中通常需要解决的问题有两个，一个是渡河时间，一个是航线的长度。

二、下面分析处理问题的方法

由于讨论的实际运动为两个分运动合成的结果，所以应该使用矢量合成法则，即平行四边形定则、三角形定则、正交分解法处理相关问题；数学运算可能用到三角函数、勾股定理、正弦或余弦定理等。

设河水的流速为vs，船在静水中的速度为vc，船头与水流方向的夹角(航向)为θ(0°<θ<180°)，船航行对地的实际速度为v，与河岸的夹角为α，河的宽度为d。

通用方法如图所示：

图1

图2

方法一：在图1中，根据平行四边形定则或三角形定则，由几何知识可知：

渡河所用时间为：

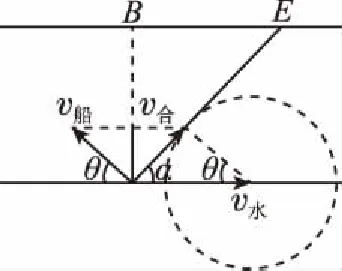
方法二：在图2中，用正交分解法的思想，将船对水的速度分解为：

垂直河岸的速度：v1=vcsinθ

沿河岸方向速度：v2=vs+vccosθ，这两个分运动具有同时性。

船在航线上的速度：

沿水流方向移动的位移：

航线长度：

以上两种分析方法，很明显第二种正交分解法在解决问题思路及计算更为简单，下面我们以正交分解法的方法来研究小船渡河的具体问题。

1.先分析研究渡河时间：

图3

2.接着再来看航线的长度：

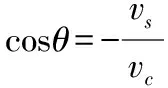
图4

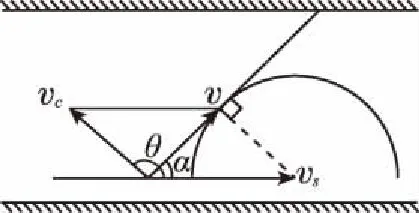
图5

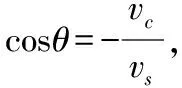
重要提示：最小位移与最短时间是渡河的两种情况，时间最短与位移最短不会同时发生！

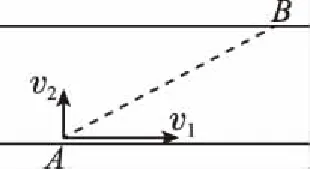
【例1】一条宽度为L的河，已知船在静水中速度为v船，水流速度为v水，那么：

(1)怎样渡河时间最短；

(2)若v船>v水，怎样渡河位移最小， 所用时间为多少；

(3)若v船

【分析与解答】(1)如前面分析，船头与河岸垂直渡河，渡河时间最短，则有：

图6

图7

【例2】如图8所示，甲、乙两船在同一条河流中同时渡河，河的宽度为L，河水流速为u，划船速度均为v，出发时两船相距2L，甲、乙船头均与岸边成60°角，且乙船恰好能直达正对岸的A点，则下列判断正确的是

( )

图8

A．甲、乙两船到达对岸的时间相等

B．两船可能在未到达对岸前相遇

C．甲船在A点右侧靠岸

D．甲船也在A点靠岸

【答案】A

图9

【例3】如图10所示，某河流中河水的速度大小v1=2 m/s，小船相对于静水的速度大小v2=1 m/s。现小船船头正对河岸渡河，恰好行驶到河对岸的B点，若小船船头指向上游某方向渡河，则小船

( )

图10

A．到达河对岸的位置一定在B点的右侧

B．到达河对岸的位置一定在B点的左侧

C．仍可能到达B点，但渡河的时间比先前长

D．仍可能到达B点，但渡河的时间比先前短

图11

【分析与解答】由题意知，小船到达B点，知小船的合速度沿AB方向，若小船船头指向上游某方向渡河时，当合速度能沿AB方向，小船就可以到达B点，如图11所示，故小船可以到达B点，由于在垂直岸方向的速度减小，故渡河时间变长，所以ABD错误，C正确。

【答案】C