牛顿第二定律在系统中的应用

陕西 孙冬子 贾安娜

牛顿第二定律是牛顿运动定律的核心，同时也是高考考查的重点内容，而在高中阶段，我们经常只将牛顿第二定律应用于单个物体或由运动状态相同的物体所组成的系统，而对于由运动状态不同的物体所组成的系统我们更多地使用整体法、隔离法，那么对于此类系统能否应用牛顿第二定律呢？本文将举例说明。

如图1所示，质量为m1的长木板和质量为m2的滑块叠放在粗糙的水平面上，长木板与地面间动摩擦因数为μ，某时刻分别给长木板和滑块一瞬时冲量，让它们以不同的初速度开始运动，设运动过程中长木板和滑块的加速度分别为a1和a2，长木板受到滑块施加的摩擦力为f1,滑块受到长木板施加的摩擦力为f2，分别以长木板和滑块为研究对象，由牛顿第二定律得

图1

m1a1=μ(m1+m2)g+f1

m2a2=f2

上面两式左右相加得：

m1a1+m2a2=μ(m1+m2)g+f1+f2

由牛顿第三定律知f1与f2等大反向，因此有

m1a1+m2a2=μ(m1+m2)g

由上式得，系统所受合外力等于系统内各物体质量与其加速度乘积的矢量和。由此可见，牛顿第二定律同样可以应用于由运动状态不同的物体所组成的系统。

【例题】如图2所示，倾角为θ的固定光滑斜面上有一可自由滑动、质量为M的木板，木板上站着一个质量为m的人，求：

图2

(1)为了使木板与斜面保持相对静止，人运动的加速度；

(2)为了使人与斜面保持相对静止，木板运动的加速度？

【解析】解法一：

(1)为了使木板与斜面保持相对静止，人应给木板施加沿斜面向上的摩擦力f，所以人应加速向下跑。设人沿斜面向下加速度为a人，现分别对木板和人应用牛顿第二定律。

木板和人受力如图3甲、乙所示，有

图3

木板沿斜面方向Mgsinθ=f

人沿斜面方向mgsinθ+f′=ma人

且f=f′

(2)为了使人与斜面保持静止，木板应给人施加沿斜面向上的摩擦力f′，所以人相对木板向上跑，而木板相对斜面加速下滑，设木板沿斜面向下的加速度为a木，现分别对人和木板应用牛顿第二定律。

木板和人受力如图4甲、乙所示

图4

木板沿斜面方向Mgsinθ+f=Ma木

人沿斜面方向mgsinθ=f′

且f=f′

解法二：

(1)以人和木板组成的系统为研究对象，木板与斜面保持相对静止，所以木板的加速度为零，为了使木板与斜面保持相对静止，人应加速向下跑，设人沿斜面向下加速度为a人，现对木板和人组成的系统应用牛顿第二定律。

木板和人组成的系统受力如图5所示，则对系统应用牛顿第二定律有

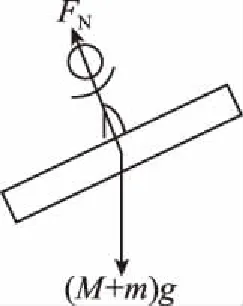
图5

(M+m)gsinθ=ma人

(2)同理，以人和木板组成的系统为研究对象，人与斜面保持相对静止，所以人的加速度为零，为了使人与斜面保持相对静止，人应相对于木板向上跑，木板沿斜面加速下滑，设木板沿斜面向下加速度为a木，现对木板和人组成的系统应用牛顿第二定律。

木板和人组成的系统受力如图5所示

(M+m)gsinθ=Ma木

【变式】如图所示，质量为M′,倾斜角为θ，且上表面光滑的斜面体静止在粗糙水平面上，斜面上有一质量为M的长木板，长木板上站了一个质量为m的人，求:

图6

(1)当人相对斜面加速向下跑时，长木板、斜面体相对水平面静止，则斜面体受到的支持力和摩擦力分别为多大；

(2)当人相对长木板向上跑时，人、斜面体相对水平面静止，则斜面体受到的支持力和摩擦力分别为多大？

【解析】解法一：

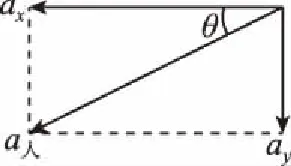
图7

水平方向有fx=ma人cosθ=(M+m)gsinθcosθ。

竖直方向有mg-fy=ma人sinθ

fy=mg-(M+m)gsin2θ

由于长木板、斜面体处于平衡状态，所以将两者看作一整体，由牛顿第三定律可知，人对整体有水平向右和竖直向下的作用力，大小分别与fx和fy相等，设斜面体受到水平面的支持力和摩擦力分别为f支和f摩，整体受力如图8所示。由平衡关系可得

(M′+M)g图8

水平方向有f摩=fx=(M+m)gsinθcosθ

竖直方向有

f支=fy+(M′+M)g

=(M′+M+m)g-(M+m)gsin2θ

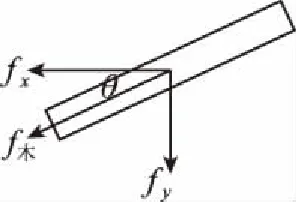
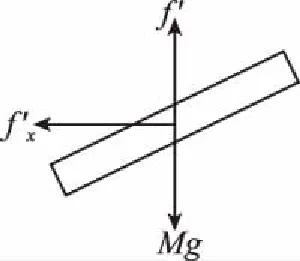
图9 图10

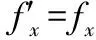
fx=f木cosθ

fy=f木sinθ

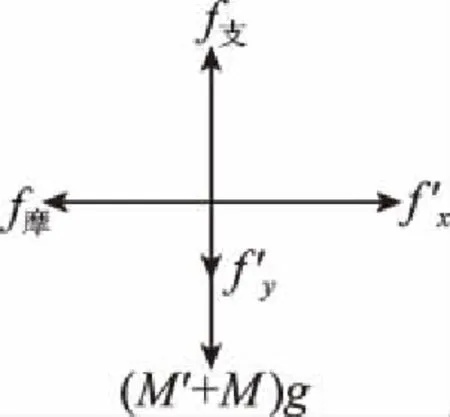
图11

竖直方向有

=(M′+M+m)g-(M+m)gsin2θ

解法二：

水平方向有f摩=ma人cosθ=(M+m)gsinθcosθ

竖直方向有(M′+M+m)g-f支=ma人sinθ

f支=(M′+M+m)g-(M+m)gsin2θ

(2)同理可得

水平方向有f摩=Ma木cosθ=(M+m)gsinθcosθ

竖直方向有(M′+M+m)g-f支=Ma木sinθ

f支=(M′+M+m)g-(M+m)gsin2θ