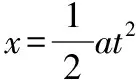解决直线运动类问题的六种常用方法

甘肃 苏入荣

在处理直线运动的某些问题时，如果采取常用解法，解答繁琐且易出错，如果从另外的角度巧妙入手，反而能使问题的解决快速、简捷，下面结合实例介绍几种处理直线运动问题的方法和技巧。

一、假设法

假设法是一种科学的思维方法，这种方法的要领是以客观事实(如题设的物理现象及其变化)为基础，对物理条件、物理状态或物理过程等进行合理的假设，然后根据物理概念和规律进行分析、推理和计算，从而使问题迎刃而解。在物理解题中，假设法有较广泛的应用，有助于我们寻求解题途径，便于简捷求得答案。

( )

图1

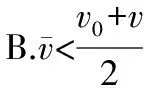
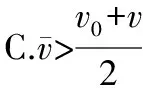
D.无法确定

【技法运用及解析】假设物体做初速度为v0、末速度为v的匀变速直线运动，则其v-t图象如图2中的倾斜虚线所示。

图2

二、逐差法

在匀变速直线运动中，第M个T时间内的位移和第N个T时间内的位移之差满足xM-xN=(M-N)aT2,对纸带问题用此法尤为快捷。

【典例2】一个做匀加速直线运动的质点，在连续相等的两个时间间隔内，通过的位移分别为24 m和64 m,每一个时间间隔为4 s，求质点的初速度v0和加速度a。

【技法运用及解析】题目中出现了连续相等的时间间隔，应优先考虑用公式Δx=aT2求解。

根据题意有Δx=64 m-24 m=40 m,T=4 s

解得v0=1 m/s。

三、逆向思维法

逆向思维是解答物理问题的一种科学思维方法，把运动过程的“末态”当成“初态”,反向研究问题，可使物理情景更简单，物理公式也得以简化，从而使问题易于解决。

解决末速度为零的匀减速直线运动问题，可采用该法，即把它看作初速度为零的匀加速直线运动。这样，v0=0的匀加速直线运动的位移公式、速度公式、连续相等时间内的位移比公式、连续相等位移内的时间比公式，都可以用于解决此类问题。

【典例3】一物体以某一初速度在粗糙水平面上做匀减速直线运动，最后停下来，若此物体在最初5 s内和最后5 s内经过的路程之比为11∶5。则此物体一共运动了多长时间？

【技法运用及解析】若依据匀变速直线运动规律列式，将会出现总时间t比前后两个5 s的和10 s是大还是小的问题;若t>10 s,可将时间分为前5 s和后5 s与中间的时间t2，经复杂运算得t2=-2 s,再得出t=8 s的结论。若用逆向的初速度为零的匀加速直线运动处理，将会简便得多。

将物体运动视为反向的初速度为零的匀加速直线运动，则最后5 s内通过的路程为

最初5 s内通过的路程为

由题中已知的条件x1∶x2=11∶5得

(10t-25)∶25=11∶5

解得物体运动的总时间t=8 s。

四、平均速度法

在匀变速直线运动中，物体在t时间内的平均速度等于物体在这段时间内的初速度v0和末速度v的算术平均值，也等于物体在t时间内中间时刻的瞬时速度，即有

如果将这两个推论加以利用，可以使某些问题的求解更为简捷。

【典例4】一个小球从斜面顶端无初速度下滑，接着又在水平面上做匀减速直线运动，直至停止，它共运动了10 s，斜面长4 m，在水平面上运动的距离为6 m。求：

(1)小球在运动过程中的最大速度;

(2)小球在斜面和水平面上运动的加速度大小。

【技法应用及解析】小球在斜面上做匀加速直线运动，在斜面底端速度最大，设最大速度为vmax，在斜面上的运动的时间为t1，在水平面上运动的时间为t2。则：

vmax=2 m/s

五、图象法

图象法是物理研究中常用的一种重要方法，可直观地反映物理规律，分析物理问题。在物理图象意义的基础上，用图象法分析解决有关问题(如往返运动、定性分析等)会显示出独特的优越性，解题既直观又方便。需要注意的是v-t图象中，图象和坐标轴围成的“面积”应该理解成物体在该段时间内发生的位移。

【典例5】已知O、A、B、C为同一直线上的四点，AB间的距离为L1，BC间的距离为L2。一物体自O点由静止出发，沿此直线做匀加速运动，依次经过A、B、C三点。已知物体通过AB段与BC段所用时间相等。求O与A的距离。

【技法应用及解析】设物体经过A点时的时刻为t0，建立物体运动的v-t图象如图3所示，则三角形Ot0a的面积为OA间的距离s，三角形O(t0+t)b的面积为OB间的距离s+L1，三角形O(t0+2t)c的面积为OC间的距离s+L1+L2，由于上述三角形相似，由面积比等于相似比的平方得

图3

六、比例法

初速度为零的匀加速直线运动的几个推论都是比例关系，在处理初速度为零的匀加速直线运动和末速度为零的匀减速直线运动时，首先考虑使用相关推论求解，简化运算。

【典例6】一列火车由静止开始做匀加速直线运动，一个人站在第1节车厢前端旁的站台前观察，第1节车厢通过他历时2 s，全部车厢通过他历时8 s，忽略车厢之间的距离，车厢长度相等，则第9节车厢通过他所用时间为多少？这列火车共有多少节车厢？

【技法运用及解析】根据初速度为零的匀加速直线运动的推论有

可得第9节车厢通过观察者所用时间为