考虑火花效应时对杆塔冲击接地电阻计算的优化

刘 骐，鲁志伟，史 柳，姜龙杰，孔 深

(东北电力大学 电气工程学院，吉林 吉林 132012)

近年来，我国政府加大了对电网的建设，输电线路长度不断增加，输电线路雷击事故频繁发生[1].现如今有效提高线路耐雷水平的措施便是降低杆塔接地电阻，并且杆塔接地的造价只占工程总造价很小的一部分，因此设计一个合理的杆塔接地系统是减少雷击事故最经济有效的措施[2～3].实际工程中冲击接地电阻一般用CDEGS进行仿真计算，其特点是运算速度快、占内存小，因其不能够模拟冲击时土壤的火花放电效应[4]，所得冲击接地电阻值较实际值往往偏高，导致杆塔接地设计的经济性相对较差.到目前为止，国内外研究者在计算冲击接地电阻时都是在一些假设条件之下，忽略了火花放电特性的影响，只是对一些结构简单的接地体建立了简化的数学模型[4～7].针对上述情况，在研究土壤火花放电效应的原理及其所适用的情况，分析其等效模型后，研究出一种能更真实模拟接地体在受冲击时的仿真模型，并计算出更精确的冲击接地电阻.

1 冲击接地相关理论

1.1 冲击接地理论

冲击电流注入接地导体，此时接地导体的接地电阻与工频接地电阻有很大的差别，将此时的接地电阻称为冲击接地电阻[8].这是因为冲击电流幅值比工频电流高很多，会击穿接地体周围的土壤，且冲击电流的等值频率比工频高很多，冲击电流进入接地体时，其地中散流情况比工频的情况要复杂很多，冲击电流的流动过程就是一个波过程，所以最大冲击电压与最大冲击电流可能并不是在同一时刻出现.通常定义冲击接地电阻为冲击电压幅值um与电流幅值im之比，即Rch=um/im[9].由于um和im可能并不是同时出现，所以Rch并无具体物理意义.但在实际工程中，为降低反击的发生，设计时需要考虑冲击接地体上的电位，此时便要根据雷电流幅值与设计的冲击接地电阻来判断，所以Rch具有工程实际意义[10].

图1 土壤火花放电效应的物理模型

1.2 火花效应的物理模型

据统计，雷电流幅值在20 kA～200 kA之间，当冲击电流流过接地体时，内部电流密度剧增，其电场强度也随之提高，此时当接地体上的场强大于周围土壤的临界击穿场强时会发生局部放电，其效果可等效为接地体半径增大.因此接地体冲击状态下的接地电阻小于工频时的接地电阻，这种现象称为土壤火花放电效应[11～13]，其物理模型如图1所示.随着土壤电阻率的升高，火花效应的作用在输电线路杆塔接地系统这种小尺寸的地网中尤为明显，这是因为在高土壤电阻率地区，接地体受冲击时，用于流散电流的接地体的长度较低土壤电阻率地区有所增加，其纵向电感的影响也相应减小，随土壤电阻率的增加其效果所造成的地电位升在总电位升中的比例减小，接地体流过同一冲击电流时，其附近土壤的电场强度显著增大[14～16].因此，需将火花效应的影响考虑在输电线路杆塔接地系统的设计中.

1.3 国标规程中对杆塔冲击接地电阻的计算

国标GB/T50065-2011中定义接地装置的冲击系数α为冲击接地电阻Rch与工频接地电阻Rg之比，即

(1)

因此在得到接地装置的冲击系数及工频接地电阻后参照国标规程也可计算出冲击接地电阻Rch=αRg.

冲击系数α的数值与接地体的几何尺寸、冲击电流的幅值和土壤电阻率等因素有关.国标GB/T50065-2011中对杆塔接地系统接地电阻的冲击系数规定为

(2)

式中：Ii为流入接地体的冲击电流，kA；ρ为土壤电阻率，Ω·m；L为水平接地装置总长度，m.

单端注入冲击电流的水平接地体接地电阻冲击系数的计算式为

(3)

水平接地导体工频接地电阻R的计算式为

(4)

式中：h为接地体埋深，m；d为接地体直径，m，若用扁铁，其等值直径d=0.5b(b为扁钢宽度)，若用角钢，则d=0.84b(b为角钢每边宽度)；A为形状系数.

图2 接地装置的形状

两种接地装置的形状，如图2所示.其中：图2(a)的形状系数A=-0.6，L=l；图2(b)的形状系数A=1.76，L=4(l1+l2).

2 等效半径的数值计算模型

由图1可知，冲击时接地体周围的火花区域，根据电磁场基本原理，在均匀土壤中，接地体长度为l时，流过接地体的电流为I，则垂直于接地体距离为d处的电流密度为

(5)

由文献[17]可知，受冲击时火花效应区域内的电场强度En与电流密度J之间的关系为：

En=αJβ

，

(6)

式中：α为常数；β为非线性系数.文献[18]中给出了不同土壤电阻率对应α和β的值.

由公式(5)和公式(6)可以得出火花效应区域内任意一点的电场强度为

(7)

当d=r′时，即放电区域边界时，En即为临界击穿场强Ec.

在均匀土壤中，不发生火花效应时，场强与电流密度呈如下线性形式：

Ec=ρJ

.

(8)

将d=r′带入公式(7)中，由公式(7)、公式(8)得：

(9)

d=r′时，系数α为

(10)

将公式(10)带入公式(9)得冲击时火花效应的等效半径为

(11)

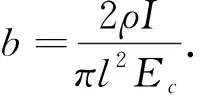
3 接地导体电感效应

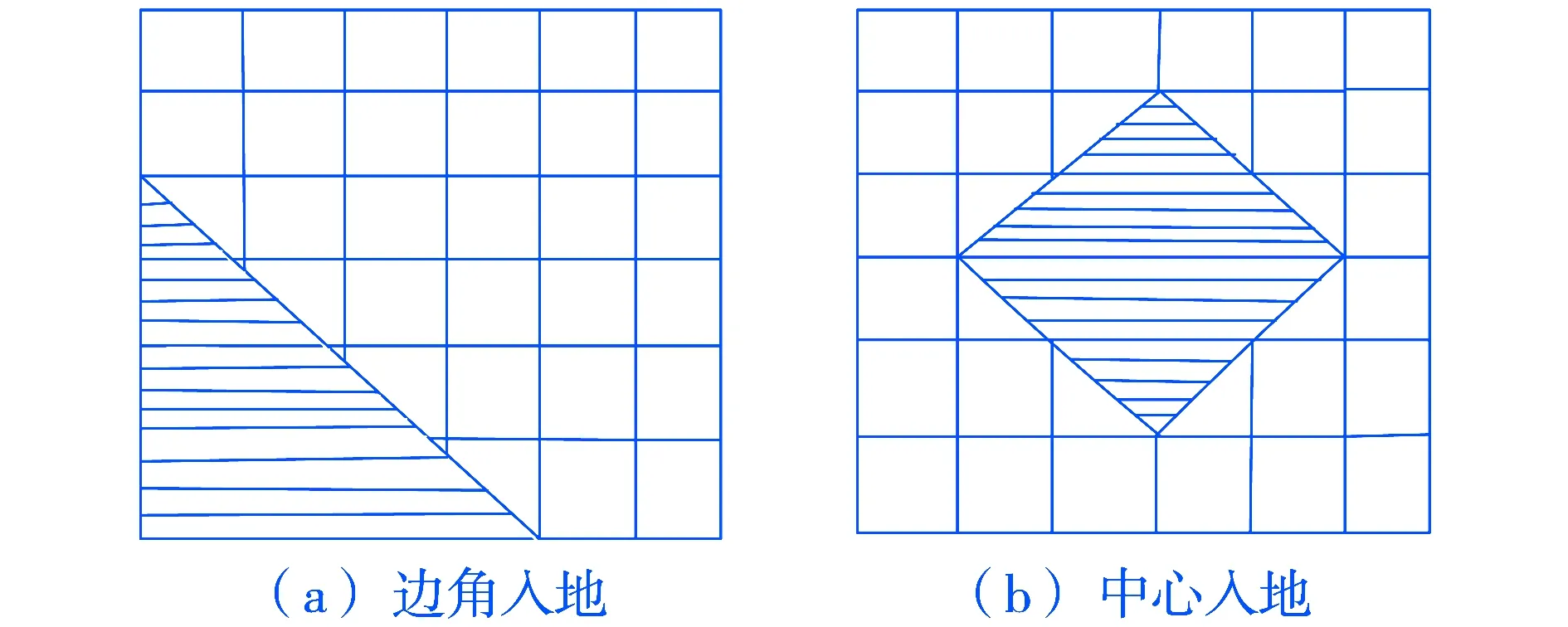
图3 地网冲击散流有效面积

接地导体在受到冲击时，除了呈现出火花效应外还会有明显的电感效应，其作用是阻碍接地导体上高频冲击电流的流动.所以在电感效应的作用下，接地网受冲击时距冲击电流注入点较远的接地导体用于流散电流的作用很小，将接地体散流明显的部分称为接地体的冲击有效长度.地网在边角和中心注入冲击电流时用于散流的有效面积，分别如图3(a)和图3(b)所示.

经本文验证，设初始长度为10 m，半径r=0.01 m，埋深h=0.8 m的水平扁钢接地体，波形为5.5/70 μs，幅值为5 kA的冲击电流由接地体中点入地，不同土壤电阻率情况时，接地体上冲击电压幅值随接地体长度的增加而变化，如图4所示.

图4 不同长度接地体对应电压幅值

由图4可得，接地体在流过冲击电流时，接地体上电压幅值有明显变化的长度仅为几十米，即冲击有效长度仅为几十米，随接地体长度的继续增加接地体上的电压幅值不再降低，即接地体的冲击接地电阻不再随接地体长度的增加而降低，所以一味扩大地网面积来降低冲击接地电阻的收效甚微.因此在保证计算精确的条件下，本文为提高运算速度在对冲击地网建模时，只对冲击有效长度内的接地体重新建模.

有效冲击接地网上分段导体用考虑火花效应后的等效半径来建模，采用辗转法来引入等效半径.在求取新接地体的等效半径时，需考虑用火花效应等效后的半径来替代实际的接地体半径建模，首先计算出原始地网接地体上每段流过的电流值，如前所述可等效出一个半径；然后以此半径建模，算出等效后地网的场强En，与土壤击穿场强Ec对比；若En远大于Ec则继续重复上述步骤，若|En-Ec|小于某一参考值，则此时的等效半径即视为火花放电时接地体的半径.

4 本文算法的验证

为验证本文算法的正确性，建立与文献[19] 所述现场试验同样的模型，采用圆钢水平接地体，半径r=0.005 m，长l=20 m的水平圆钢接地导体，埋深h=1 m，土壤电阻率ρ=1 000 Ω·m.将现场试验结果、国标规程值和运用本文算法所得结果进行对比，如表1所示.

表1 不同方法所得冲击接地电阻

由表1可得，试验结果与本文算法所得结果远小于国标规程值，这是因为国标所定冲击系数是经验公式，所以数值相对保守，其与试验结果的平均误差率为36.31%，本文算法与试验结果的平均误差为15.44%，误差率减少了20.87%，验证了本算法的正确性.由所得数据减小趋势相同，进一步验证本方法的正确性.

5 算例与分析

5.1 模型参数的选择

图5 杆塔接地网仿真模型的俯视图

本文选用国标中2.6/50 μs的标准波形，为接近

实际雷电流同时也便于观察效果明显，本文将方框四个顶点作为电流注入点，冲击电流幅值范围在20 kA～200 kA.

为接近实际杆塔的接地系统，本文所选地网模型参数：钢材导体相对磁导率ur=636，电阻率ρ=0.17 μΩ·m，半径r=0.01 m，埋深h=1 m，网孔为15 m×15 m，四角的引长线为15 m，位于网孔对角线的延长线上，如图5所示.模型中的土壤采用均匀土壤，土壤电阻率的取值范围在ρ=200 Ω·m～2 000 Ω·m.

5.2 计算结果及其分析

按上述条件运用CDEGS求得在不同土壤电阻率中对应不同冲击电流幅值的冲击接地电阻值，如表2所示.

表2 CDEGS所得冲击接地电阻

由于CDEGS无法模拟土壤火花放电，因此所求冲击接地电阻不随冲击电流幅值的变化而变化，在土壤电阻率固定时冲击接地电阻即为常数.

按上述条件运用本文算法求得在不同土壤电阻率中对应不同冲击电流幅值的冲击接地电阻值，如表3所示.

表3 本文算法所得冲击接地电阻

由表3可得，在土壤电阻率较低时，接地体的冲击接地电阻随冲击电流幅值增大而减小，但减小的数值甚微，最大变化量仅为0.35 Ω.这是因为土壤电阻率较低时，接地体上的电流散流容易，火花效应作用并不明显，与之作用相反的电感效应占主导作用；在土壤电阻率较高时，接地体的冲击接地电阻随冲击电流幅值的增大而明显减小，最大变化量达8.21 Ω，这是因为在土壤电阻率较高时，接地体上的电流不易散流，火花效应作用明显.

对比表2、表3可知，本文算法所得冲击接地电阻的值在任何土壤电阻率中均小于直接用CDEGS计算所得值，因CDEGS无法直接模拟土壤火花放电，土壤电阻率固定时，其算得的冲击接地电阻为常数，不随冲击电流幅值的变化而发生改变；在土壤电阻率较低且流过幅值较大的冲击电流时，所得冲击接地电阻与本文算法所得结果相差0.37 Ω；在土壤电阻率较高且流过幅值较大的冲击电流时，所得冲击接地电阻与本文算法所得结果相差达19.7 Ω；随冲击电流幅值增大，则接地体中电流密度越大，相应电场强度增加，土壤火花放电效果愈发明显，冲击接地电阻值则减小，所以本文考虑火花效应后所得冲击接地电阻值与实际值更为接近.

6 结 语

(1)由于电感效应的影响，在降低冲击接地电阻时单纯通过扩大地网面积收效甚微，最经济有效的方式是在不同土壤电阻率对应不同冲击有效面积内采取降阻措施.

(2)针对CDEGS在计算冲击接地电阻时存在不足，因其无法直接模拟土壤火花放电区域，使得在计算时高估了冲击接地电阻，本文在考虑了土壤击穿特性后，建立了更加准确的接地模型改善原有算法.运用本文所述方法所得结果与试验结果的误差率较国标规程推荐值与试验结果的误差率减少了20.87%，验证本文方法的正确性.

(3)本文算例显示，土壤电阻率较高时优化前后所得冲击接地电阻的结果相差达19.7 Ω，因此将该方法用于杆塔冲击接地系统设计的实际工程中具有显著的优越性.